具有传感器增益退化、随机时延和丢包的分布式融合估计器

赵国荣　　韩旭　　万兵　　闫鑫

具有传感器增益退化、随机时延和丢包的分布式融合估计器

赵国荣1韩旭1万兵1闫鑫2

研究了具有传感器增益退化、模型不确定性、数据传输时延和丢包的网络化多传感器分布式融合估计问题，模型的不确定性描述为系统矩阵受到随机扰动，传感器增益退化现象通过统计特性已知的随机变量来描述，随机时延和丢包现象存在于局部最优状态估计向融合中心传输的过程中.首先，设计了一种局部最优无偏估计器，然后将传输时延描述为随机过程，并在融合中心端建立符合存储规则的时延—丢包模型，利用最优线性无偏估计方法，导出最小方差意义下的分布式融合估计器.最后，通过算例仿真证明所设计融合估计器的有效性.

传感器增益退化，模型不确定性，传输时延，丢包，分布式融合估计

引用格式赵国荣，韩旭，万兵，闫鑫.具有传感器增益退化、随机时延和丢包的分布式融合估计器.自动化学报，2016，42（7）: 1053-1064

无线网络化多传感器融合估计以其一系列优点，已经被广泛应用于控制、目标跟踪、生物监测、信号处理和通信等领域［1-4］.然而在实际应用系统中将不可避免地存在传感器故障、模型的不确定性、时间延迟和丢包问题，使得系统融合估计性能受到严重损害.针对此类系统，已有学者将随机系统理论、时滞系统理论和融合估计理论相结合，提出了一些融合估计算法.文献［5］通过增广矩阵方法，将同时存在不确定观测、随机测量时延和多丢包现象的系统转化为无时滞系统，并利用射影理论导出最优融合估计器；考虑到文献［5］中状态维数增加将导致计算负担加重，文献［6］基于MMSE（Minimum mean square error）准则，导出了传感器失效下，既有观测时延又有状态时延的不确定系统的鲁棒Kalman滤波器.文献［7］在集中式融合框架下，对存在传感器失效、模型不确定性、观测数据包延迟和丢失情况下的融合估计问题进行了讨论，并提出两种不同的融合估计算法.文献［8］利用文献［9］的结论，在未考虑模型不确定的前提下，提出了具有传感器失效、局部最优估计传输时延和丢包下的分布式Kalman融合估计方法.

在恶劣复杂的使用环境中，除传感器失效现象外，还会出现因传感器老化、网络拥堵等原因导致的传感器增益退化［10-12］.相比于传感器失效，传感器增益退化在无线网络化多传感器融合估计系统中并未得到广泛研究，而且同时考虑传感器增益退化、模型不确定性、数据时延和丢包问题的文献极少.文献［13］在文献［14］的基础上，给出了一种传感器增益退化下，具有数据传输延迟和丢失的离散不确定系统的集中式融合估计器.集中式融合结构虽能保证融合估计性能最优，但是其容错能力较差，工程上难以实现.因此，本文在分布式融合框架下，研究了具有传感器增益退化、模型不确定性、数据传输延迟和丢包的多传感器融合估计问题.其中，模型的不确定性描述为系统矩阵受到随机扰动，传感器增益退化现象通过统计特性已知的随机变量来描述，并由此得到传感器增益退化下的量测方程，随机时延和丢包现象存在于局部最优状态估计向融合中心传输的过程中.首先，基于状态方程和量测方程，设计了一种局部最优无偏估计器，使得局部估计误差均方差最小.然后，将传输时延描述为随机过程，并在融合中心端建立符合存储规则的时延—丢包模型，利用最优线性无偏估计方法［15-18］，导出最小方差意义下的分布式融合估计器.最后，通过算例仿真证明所设计融合估计器的有效性.

1　问题描述与分析

考虑如下离散不确定线性时变随机系统：

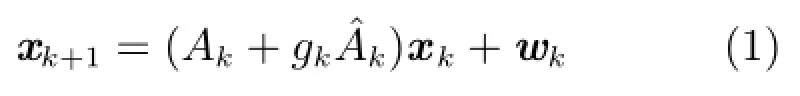
如图1所示，假设系统由N个传感器进行观测，第i个传感器的量测方程描述为：

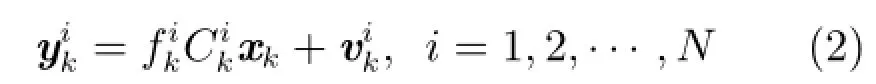
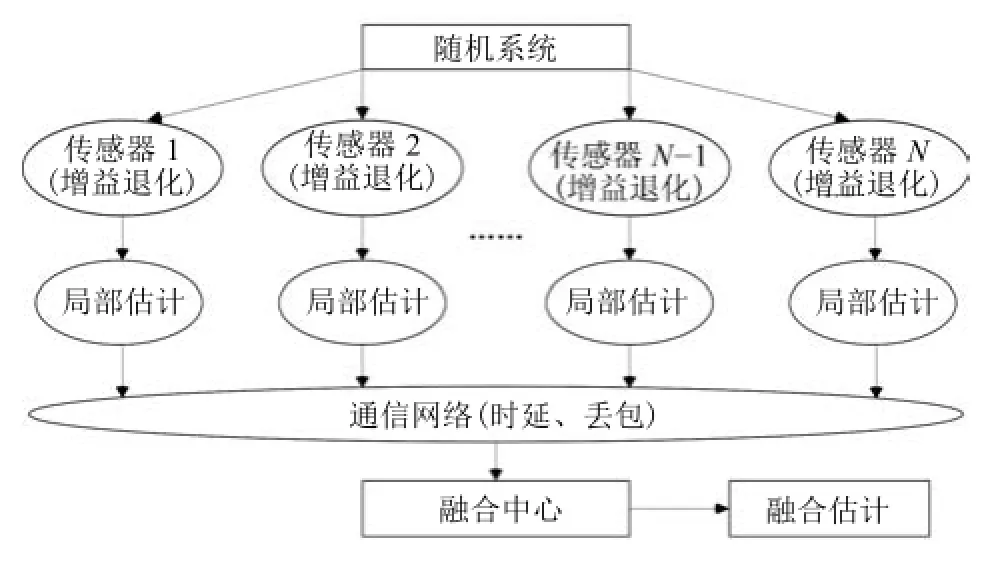
图1　分布式融合估计信号传递图Fig.1　Signal transmission of decentralized fusion estimator

不失一般性，对系统做如下假设：

假设2.初始状态x0与和均不相关，并定义

假设第i个子系统（1）和（2）的局部最优（线性最小方差意义下）状态估计记为在这里，因为标准Kalman滤波器要求系统矩阵是确定的，且系统噪声为协方差已知的白噪声，而本文所研究的系统方程（1）中，系统矩阵中存在乘性随机噪声gk，使得每一时刻系统矩阵不再是确定的，且并未假设gk是白噪声，因此标准Kalman滤波器不适合解决系统模型（1）和（2）的最优估计问题.所以，为得到具有传感器增益退化和模型不确定性子系统的局部最优状态估计，本文采用如下滤波器的形式：

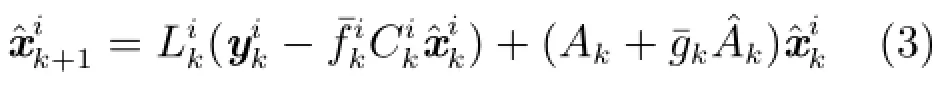
下面给出定理1证明滤波器（3）是无偏的.

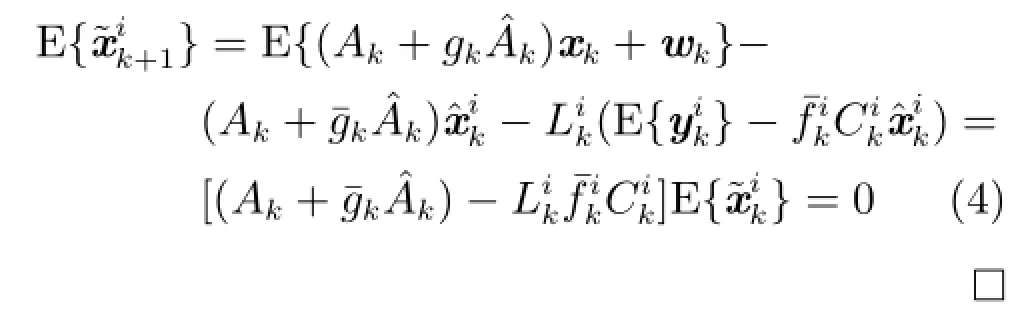
为方便运算，定义运算符号 coli（Di）：=根据最优线性无偏估计方法［15-18］，最优分布式融合估计器为：

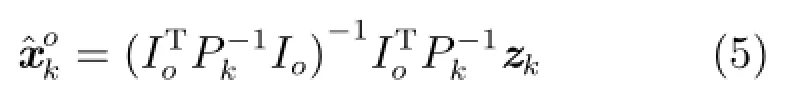
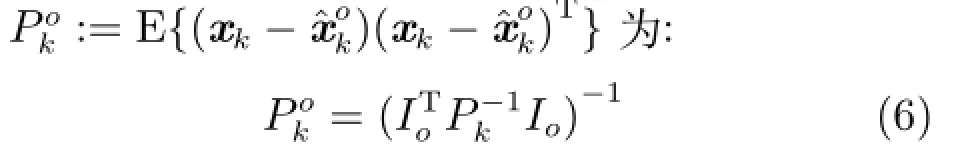
在分布式框架下，随机时延和丢包现象存在于局部最优状态估计向融合中心传输的过程中，本文将传输时延和丢包描述为：

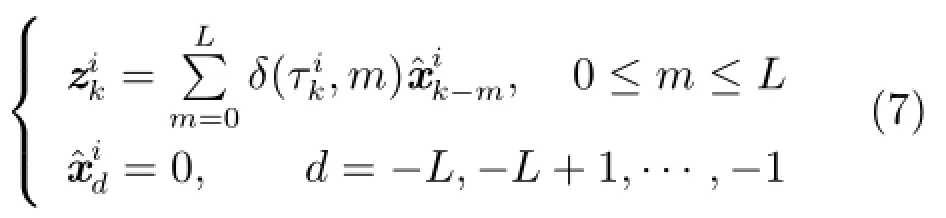
针对不同时刻数据包可能会同时到达融合中心的情况，采用文献［19］提出的信号存储原则，每个时刻的局部最优估计在被发送前已经被标记好时间顺序，融合中心根据所收到信号的标记，只存储最新时刻的数据包，丢掉其他数据包.

由于时延和丢包的存在，在k时刻，经第i通道到达融合中心的局部最优状态估计为0，1，···，L），或者发生数据丢包.因此，不能将此时的信号直接用于分布式融合估计.为此，设为 k时刻第i通道在融合中心端用于设计分布式融合估计器的局部重组状态估计，下角标“r”表示重组，“k”表示k时刻，上角标“i”表示第i通道的形式可描述为：

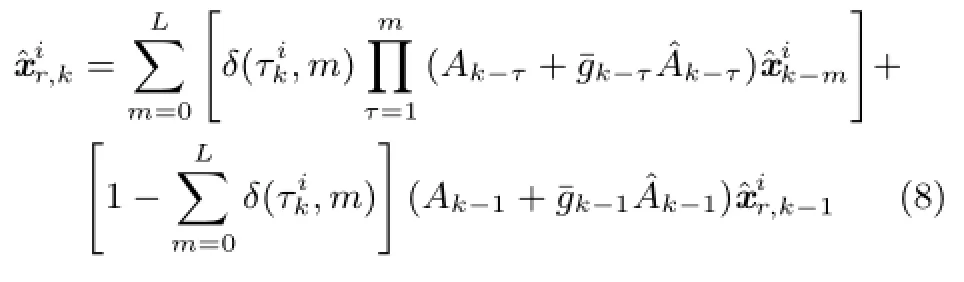
式（8）的含义为：发生时延m时，k时刻经第i通道到达融合中心的时延信号为则对应的局部重组状态估计取为的m 步预测值，即为发生数据丢包，时则取上一时刻第i通道的局部重组状态估计的一步预测值作为本时刻的局部重组状态估计，即为

针对上述具有传感器增益退化、模型不确定性、随机时延和丢包的多传感器融合估计系统，本文要解决的问题是：

2　局部最优滤波增益设计

在引出主要结论之前，首先定义如下算子：

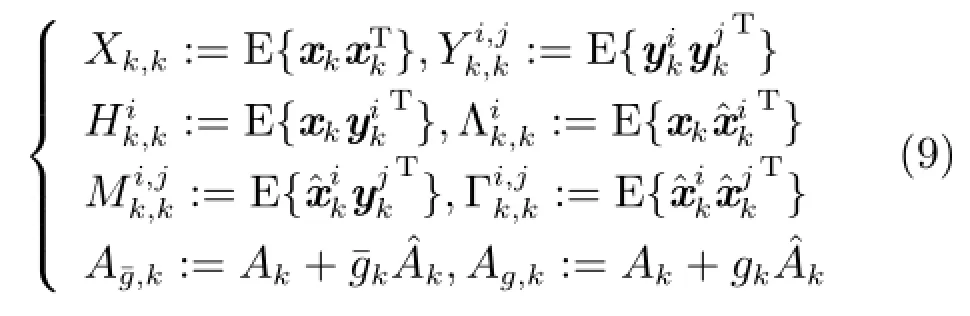
定理2.对于第i个子系统（1）和（2），使得局部滤波器（3）误差协方差最小的局部滤波增益的递推形式为：

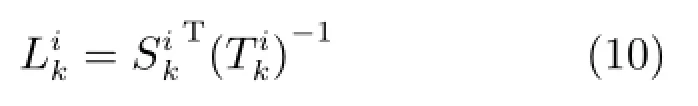
局部最优误差协方差递推形式为：

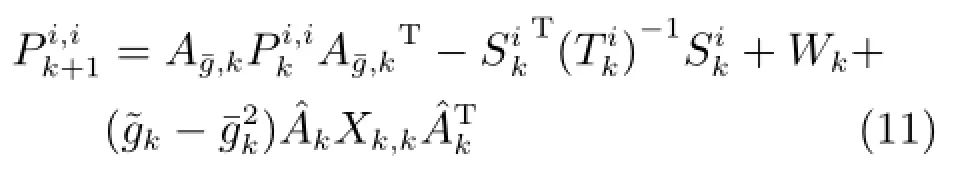
局部最优误差交叉协方差递推形式为：

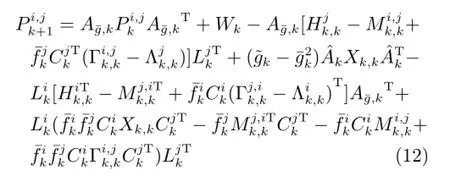
其中，各量递推公式为：

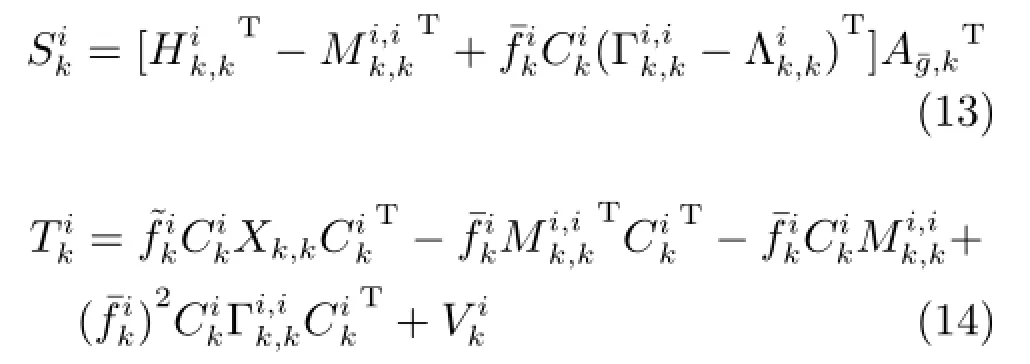
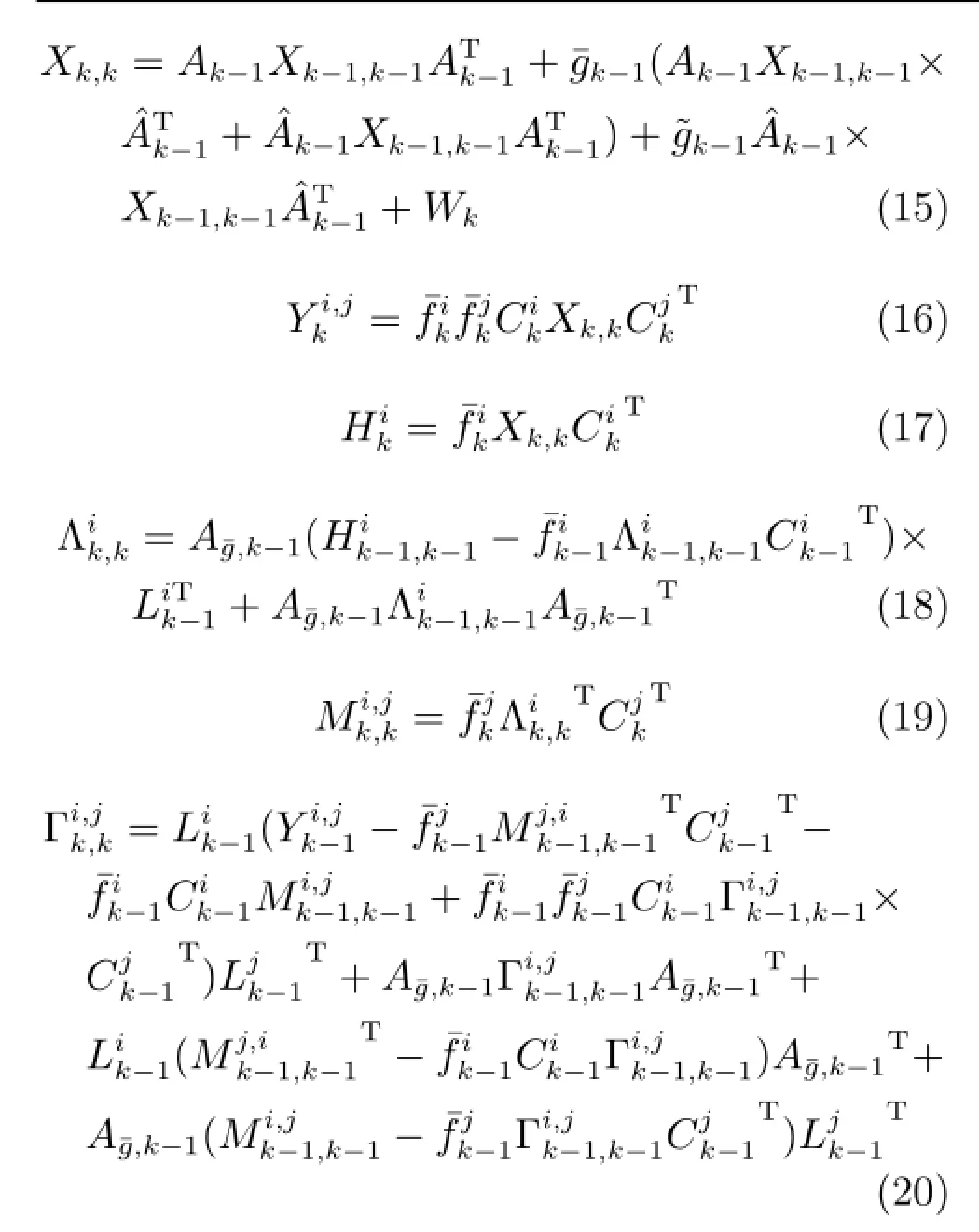
并且，根据假设2，X0，0为已知，其他变量初值设置如下：

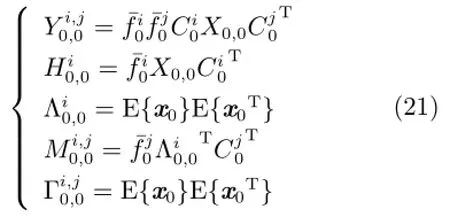
证明.下面证明式（10），由式（1）～（3）可得：

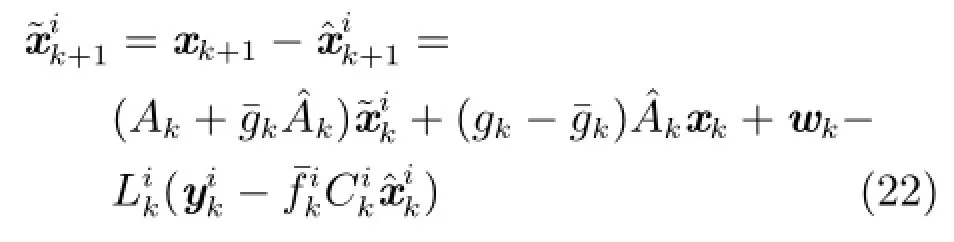
结合式（9）以及假设1和假设2，可得：

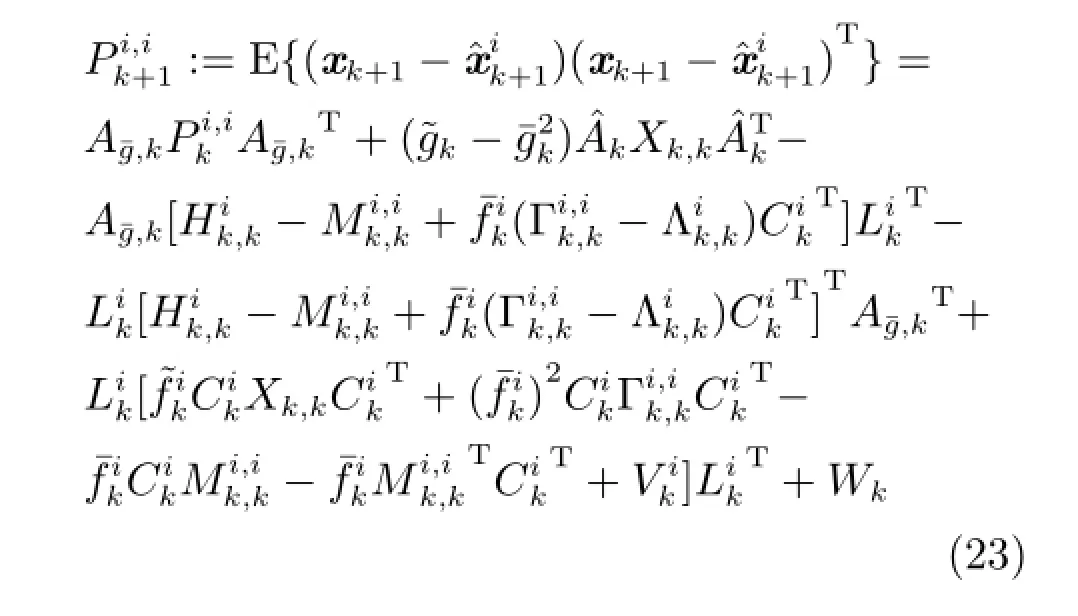
下面令

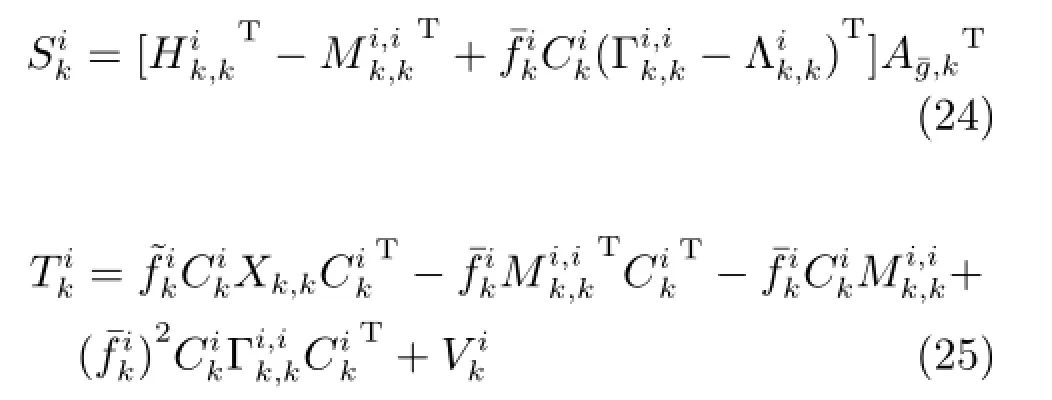
将式（24）和式（25）代入式（23）可得：

需要特别指出的是，定理2与文献［13］中提出的定理1在形式上有很多相似之处，这是因为本文求取传感器i的局部最优状态估计和文献［13］求取全局融合估计，都是基于最小方差估计方法，中间变量的定义和结论推导在形式上有相似之处，但是二者各自定义的中间变量有明显不同的意义.本文采用的是分布式融合估计，即先利用传感器i在k时刻的测量数据得到局部最优估计时延和丢包发生在传送至融合中心的过程中，定理2求取的是局部最优估计，且式（9）中各中间变量是基于传感器i定义的，未加入时延和丢包环节，而文献［13］中定理1虽采用与本文中式（3）形式一致的滤波器结构，但其采用的是集中式融合估计方法，融合中心直接利用所有传感器的测量数据进行融合估计，时延和丢包发生在测量数据传送至融合中心的过程中，所定义的各中间变量是基于全局的，具有明显的时延特征.

3　分布式融合估计器

在得到主要结论之前，首先介绍如下两个引理.

1）情况1：m=n时，

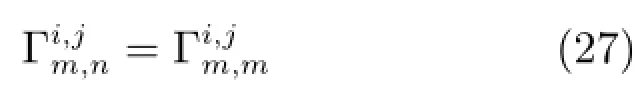
2）情况2：m-n=1时，

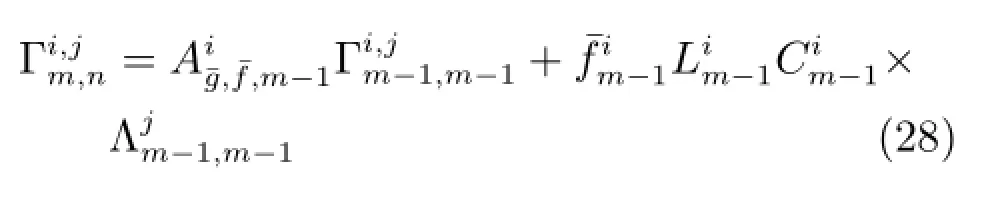
4）情况4：n-m=1时，

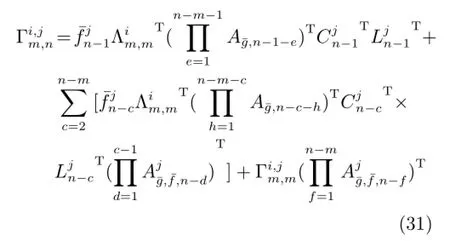
1）情况1：m=n时，

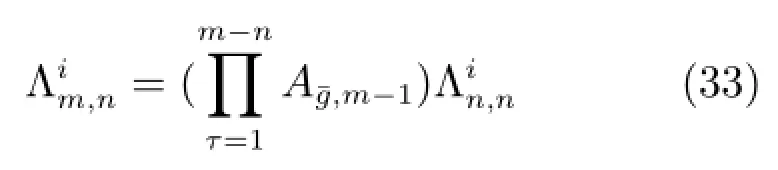
3）情况3：n-m=1时，

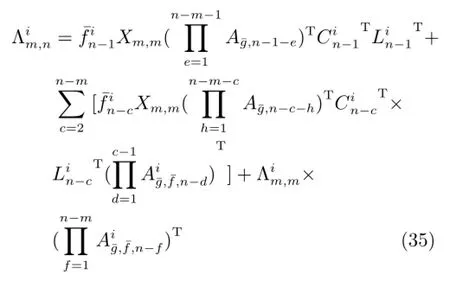
由于引理1证明过程较繁琐，为增加文章可读性，具体证明过程见附录A.

四是注重心理素质健康教育培训。针对监狱戒毒警察工作生活中面临的监管安全压力、执法安全压力等导致的心理问题，河南省司法厅联合高校举办由政工干部和基层业务骨干参加的心理健康教育能力素质提升培训班，引导政工干部把心理矫治的手段运用到干部思想政治工作中，引导基层一线警察掌握释放自我、缓解压力的手段和方法。各直属单位也把队伍心理健康教育作为教育培训的重要内容，定期邀请社会心理咨询专家或利用单位内部心理咨询师对警察开展心理辅导、心理知识讲座、心理咨询、心理拓展、心理矫治等心理素质培训，使队伍掌握应对压力和解决心理问题的方法技巧，有效缓解工作生活压力，提升心理健康水平。

引理2.定义如下变量：

则有下式成立：

由于引理2证明过程较繁琐，为增加文章可读性，具体证明过程见附录B.

证明.由式（1）和式（8）可得：

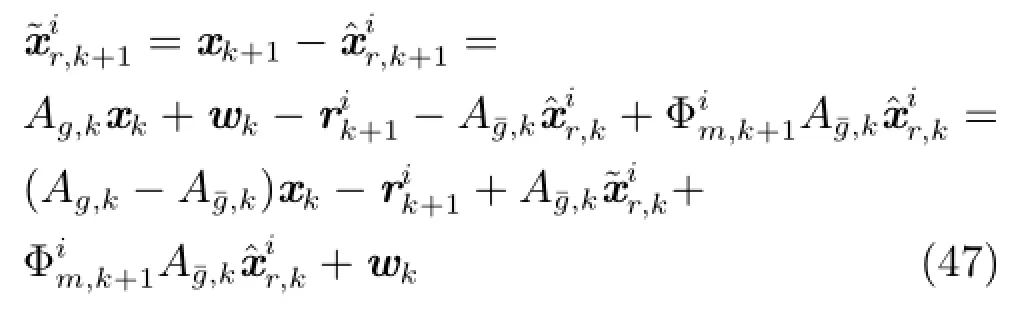
则可得：

1）当i =6j时，

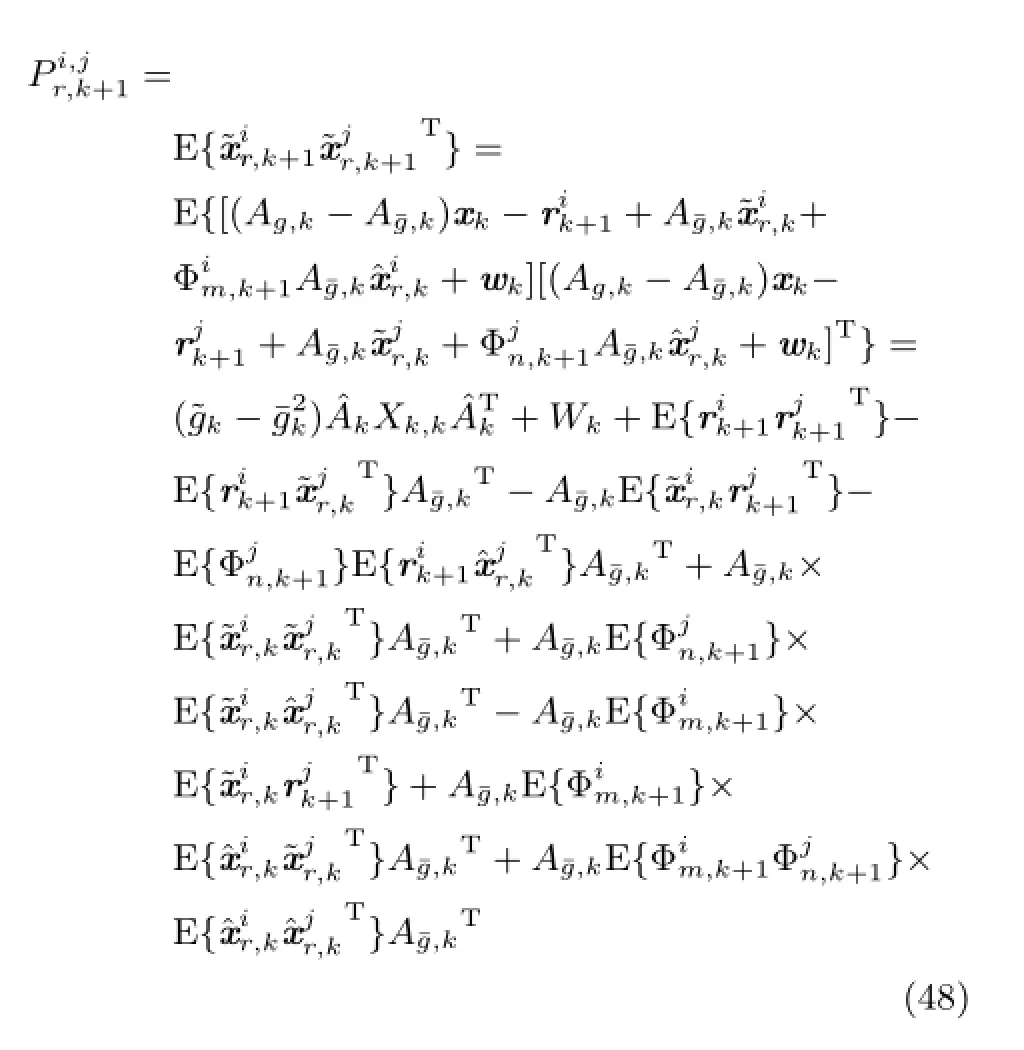
利用式（36）对式（48）和式（49）中各量进行变量代换，即得到式（46）.□

根据最优线性无偏估计方法，基于所设计的局部滤波增益（10）及相应融合中心端的N个局部重组状态估计xˆir，k，由式（5）和式（6），可得到分布式融合估计器的形式如下：

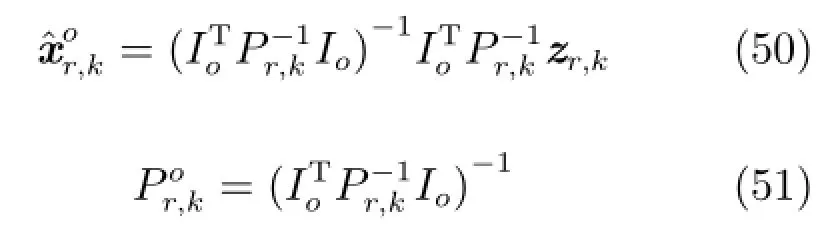
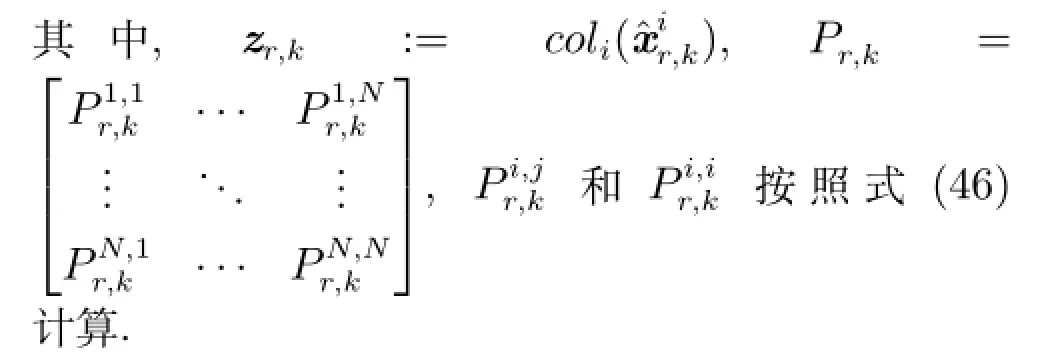
4　算例仿真

考虑如下由2个传感器组成的线性时变离散随机系统：

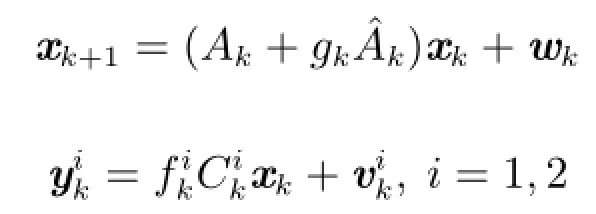
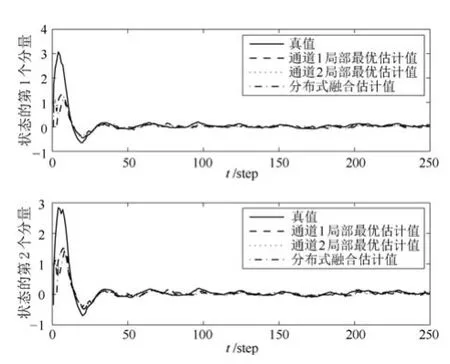
图2　状态xk和状态估计ˆxor，k的轨迹Fig.2　Trajectories of state xkand state estimate

为比较本文所提出的分布式融合估计方法与文献［13］所提出的集中式融合方法下的估计性能，设传感器增益退化系数在区间Df=［0.6，0.8］上服从均匀分布，乘性噪声gk在区间Dg=［-0.1，0.1］上服从均匀分布，分别计算出两种融合估计方法下的融合估计误差协方差矩阵的迹，其仿真结果如图6所示.由图6可看出，文献［13］中所提出的集中式融合估计方法的融合估计误差小于本文所提的分布式融合方法，这是因为前者采用集中式框架，在融合中心直接利用所有传感器的原始测量数据进行融合估计，测量数据信息损失量最小，后者首先利用各传感器测量数据进行局部最优估计，然后再将局部最优估计发送到融合中心，测量数据信息损失量大于集中式融合方法，从而增大融合估计误差；从图5又可以看出，两种方法的融合估计误差相差不大，说明本文提出分布式融合结构相比于集中式融合估计，虽然融合精度并不是最优，但融合精度损失不大，同时，采用分布式计算方法，能够避免高维矩阵计算，降低了计算量.

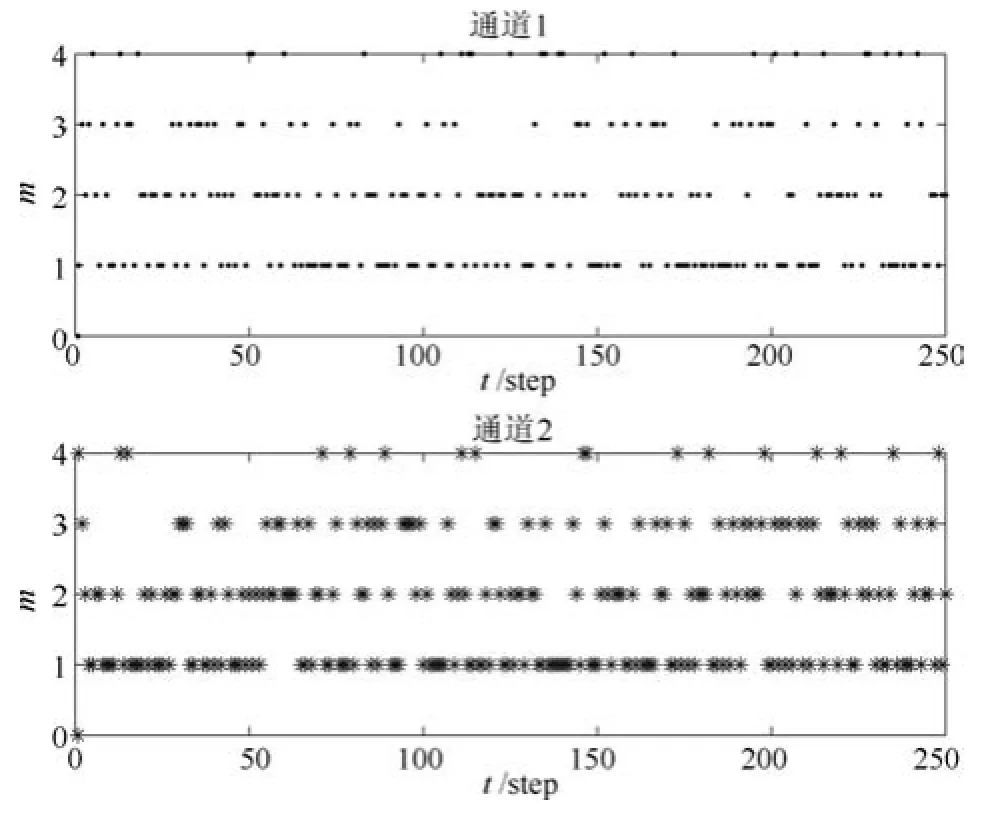
图3　各时刻随机时延m依概率的分布Fig.3　Distribution of the random time delay m based on probability every step

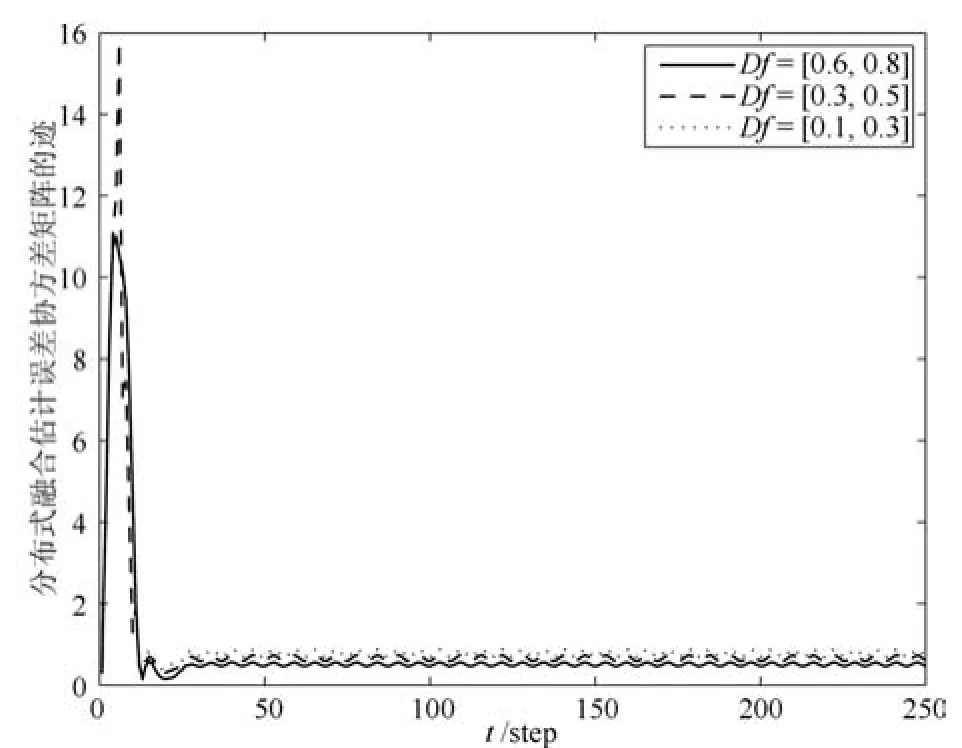
图4　增益退化系数与的关系Fig.4　Relationship between gain degradation coefficient

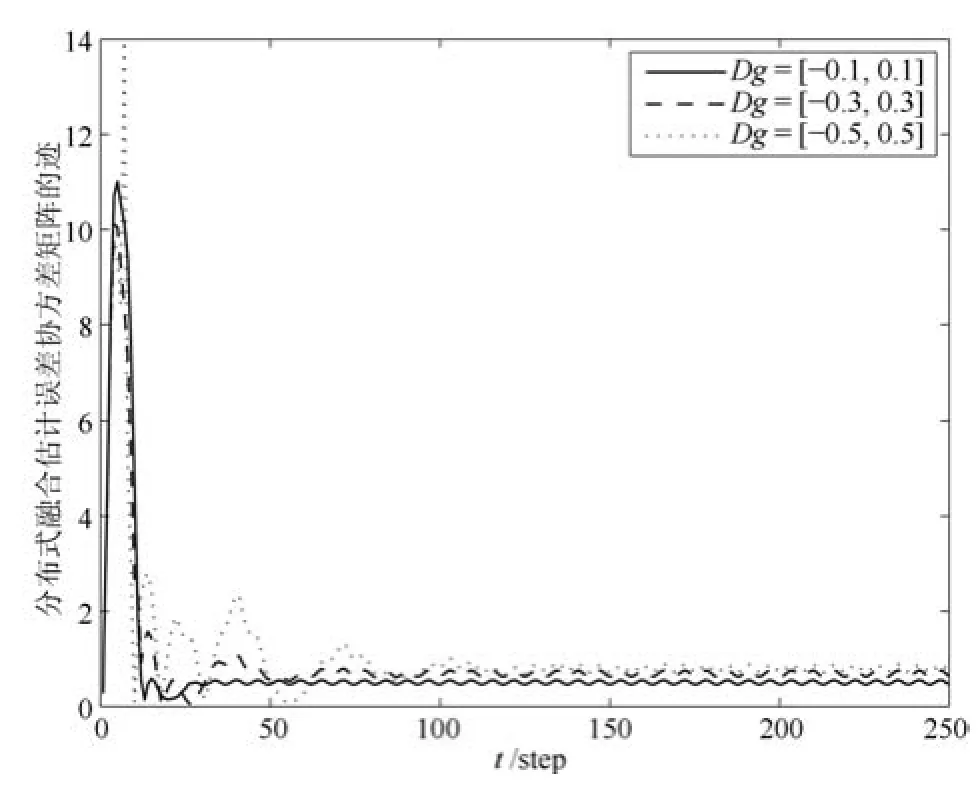
图5　乘性噪声gk与）的关系Fig.5　Relationship between multiplicative noise

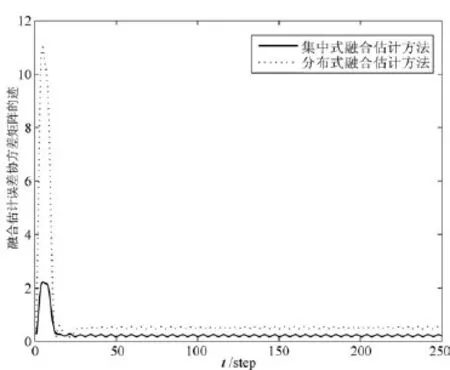
图6　分布式融合估计方法与集中式融合估计方法对比Fig.6　Comparison of decentralized fusion estimator with centralized fusion estimator

5　结论

本文考虑了具有传感器增益退化、模型不确定性、数据传输时延和丢包的多传感器分布式融合估计问题，对模型的不确定性、传感器增益退化现象、随机时延和丢包现象依次进行建模.针对传感器增益退化和模型的不确定性，设计了一种局部最优无偏估计器，并在融合中心端建立符合存储规则的时延—丢包模型，利用最优线性无偏估计方法，推导出最小方差意义下的分布式融合估计器的递推形式.最后仿真结果表明，传感器增益退化程度和模型不确定性越大，系统融合估计精度越差.因此，可通过改善传感器抗退化性能和减小模型不确定性，来提高系统融合估计精度.相比于集中式融合估计，本文所提方法能够有效降低计算量，提高了系统容错能力和抗干扰性，且工程上易于实现.

附录A引理1的证明过程

证明.首先依次对第3节中式（27）～（31）进行推导，即分5种情况进行讨论:

此时，由式（A4）可得

4）当n-m=1时，与式（28）推导过程同理，可得

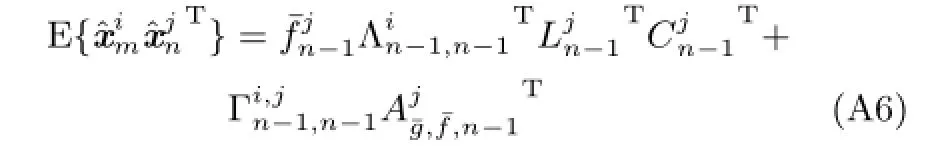
5）当n-m≥2时，与式（29）推导过程同理，可得

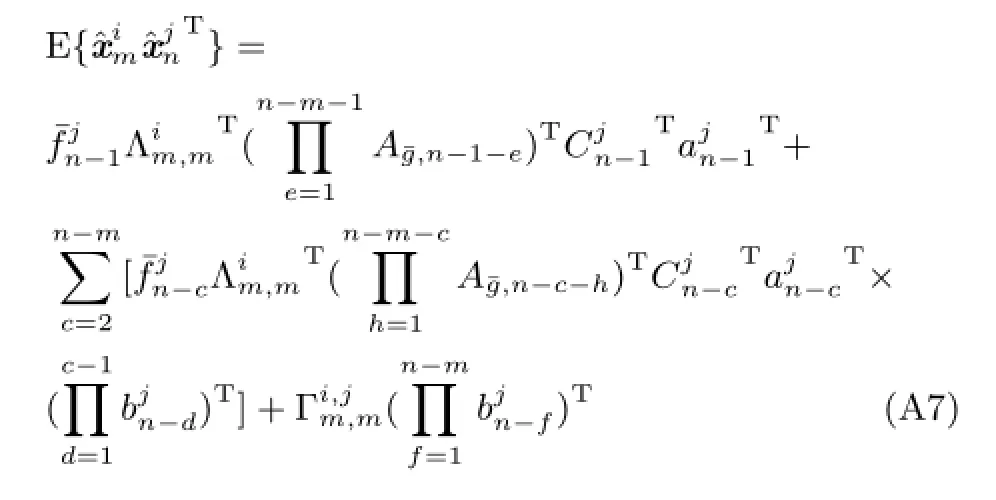
利用式（A3）对式（A5）和式（A7）进行变量代换，并综合上述5种情况下讨论结果，得到式（27）～（31）.

下面对正文中式（32）～（35）进行推导，即分4种情况进行讨论:

1）当m=n时，有

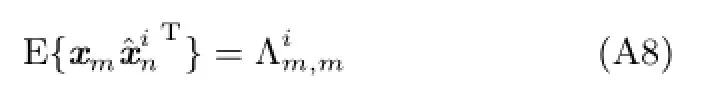
2）当m-n≥1时，有

3）当n-m=1时，有

4）当n-m≥2时，令

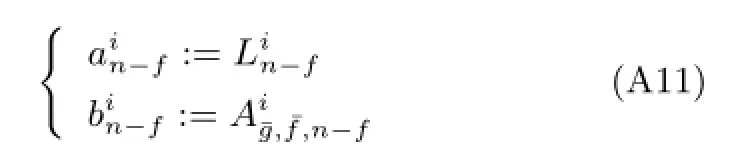
则由式（A4）推导过程可得

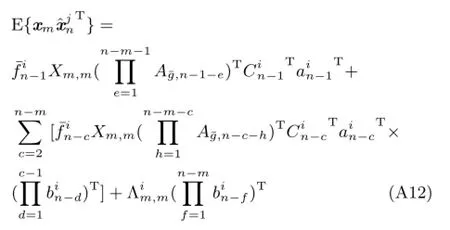
利用式（A11）对式（A12）进行变量代换，并综上4种情况所述，得到式（32）～（35）.□

附录B引理2的证明过程

证明.下面分别对第3节中式（37）～（45）依次进行推导.由式（36）中各变量定义可得到

1）当m=0时，有

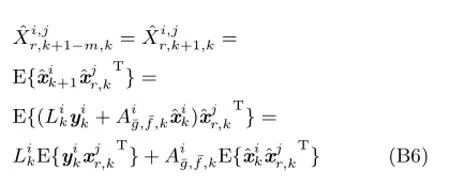
2）当m=1时，有

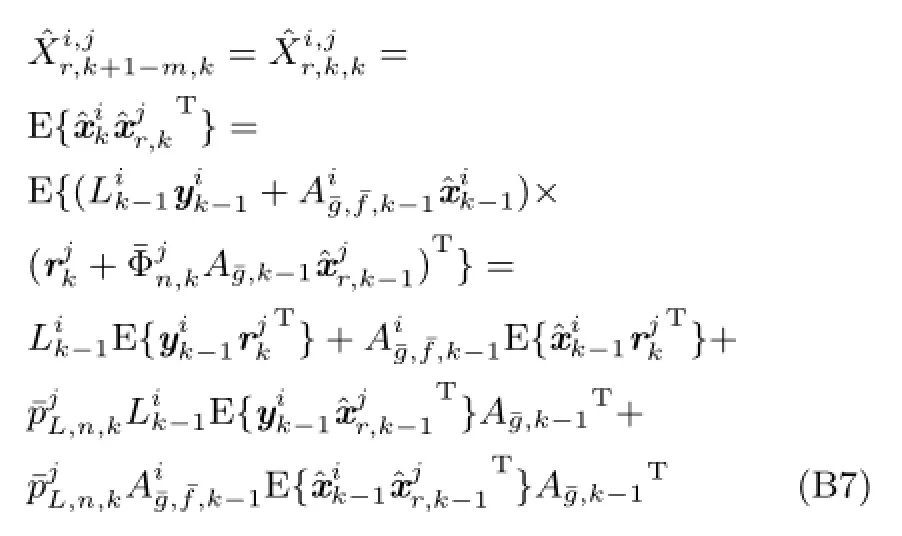
3）当m>1时，由式（8）得

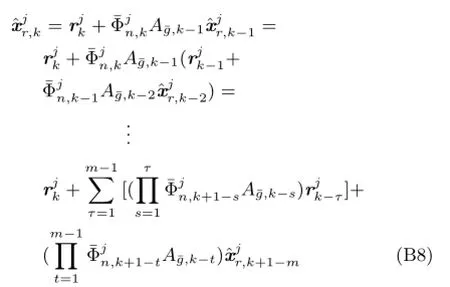
则有

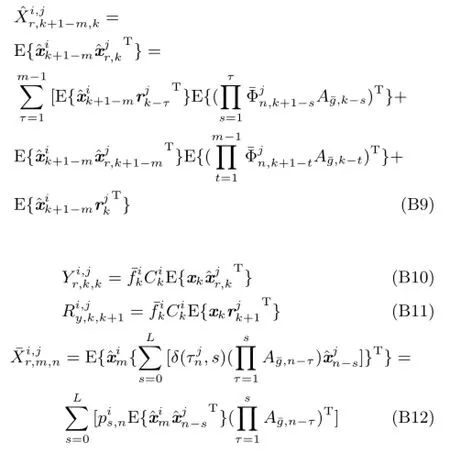
利用式（36）对式（B1）～（B7）、式（B9）～（B12）中各量进行变量代换，即分别得到式（37）～（45）.□

References

1 Ge Quan-Bo，Li Wen-Bin，Sun Ruo-Yu，Xu Zi.Centralized fusion algorithms based on EKF for multisensor non-linear systems.Acta Automatica Sinca，2013，39（6）：816-825（葛泉波，李文斌，孙若愚，徐姿.基于EKF的集中式融合估计研究.自动化学报，2013，39（6）：816-825）

2 Feng Xiao-Liang，Wen Cheng-Lin，Liu Wei-Feng，Li Xiao-Fang，Xu Li-Zhong.Sequential fusion finite horizon H∞filtering for multisenor system.Acta Automatica Sinca，2013，39（9）：1523-1532（冯肖亮，文成林，刘伟峰，李晓芳，徐立中.基于多传感器的序贯式融合有限域H∞滤波方法.自动化学报，2013，39（9）：1523-1532）

3 YueYuan-Long，ZuoXin，LuoXiong-Lin.Improving measurement reliability with biased estimation for multisensor data fusion.Acta Automatica Sinca，2014，40（9）：1843-1852（岳元龙，左信，罗雄麟.提高测量可靠性的多传感器数据融合有偏估计方法.自动化学报，2014，40（9）：1843-1852）

4 Chen B，Zhang W A，Yu L，Hu G Q，Song H Y.Distributed fusion estimation with communication bandwidth constraints.IEEE Transactions on Automatic Control，2015，60（5）：1398-1403

5 Ma J，Sun S L.Centralized fusion estimators for multisensor systems with random sensor delays，multiple packet dropouts and uncertain observations.IEEE Sensors Journal，2013，13（4）：1228-1235

6 Chen Bo，Yu Li，Zhang Wen-An.Robust Kalman filtering for uncertain discrete time-delay systems with missing measurement.Acta Automatica Sinica，2011，37（1）：123-128（陈博，俞立，张文安.具有测量数据丢失的离散不确定时滞系统鲁棒Kalman滤波.自动化学报，2011，37（1）：123-128）

7 Chen B，Yu L，Zhang W A.Robust Kalman filtering for uncertain state delay systems with random observation delays and missing measurements.IET Control Theory and Applications，2011，5（17）：1945-1954

8 Chen B，Zhang W A，Yu L.Distributed fusion estimation with missing measurements，random transmission delays and packet dropouts.IEEE Transactions on Automatic Control，2014，59（7）：1961-1967

9 Sun S L，Deng Z L.Multi-sensor optimal information fusion Kalman filter.Automatica，2004，40（6）：1017-1023

10 Soomon I S D，Knight A J.Spatial processing of signals received by platform mounted sonar.IEEE Journal of Oceanic Engineering，2002，27（1）：57-65

11 Yalcin H，Collins R，Hebert M.Background estimation under rapid gain change in thermal imagery.Computer Vision and Image Understanding，2007，106（2-3）：148-161

12 Zhou D H，He X，Wang Z D，Liu G P，Ji Y D.Leakage fault diagnosis for an internet-based three-tank system：an experimental study.IEEE Transactions on Control Systems Technology，2012，20（4）：857-870

13 Liu Y，He X，Wang Z D，Zhou D H.Optimal filtering for networked systems with stochastic sensor gain degradation. Automatica，2014，50（5）：1521-1525

14 Wang Z D，Yang F W，Ho D W C，Liu X H.Robust H∞filtering for stochastic time-delay systems with missing measurements.IEEE Transactions on Signal Processing，2006，54（7）：2579-2587

15 Li X R，Zhu Y M，Wang J，Han C Z.Optimal linear estimation fusion I：unified fusion rules.IEEE Transactions on Information Theory，2003，49（9）：2192-2208

16 Carlson N A.Federated square root filter for decentralized parallel processors.IEEE Transactions on Aerospace and Electronic Systems，1990，26（3）：517-525

17 Deng Z L，Qi R B.Multi-sensor information fusion suboptimal steady-state Kalman filter.Chinese Science Abstracts，2000，6（2）：183-184

18 Zhao Guo-Rong，Han Xu，Lu Jian-Hua.A decentralized fusion estimator using data-driven communication strategy subject to bandwidth constraints.Acta Automatica Sinica，2015，41（9）：1649-1658（赵国荣，韩旭，卢建华.一种基于数据驱动传输策略的带宽受限的分布式融合估计器.自动化学报，2015，41（9）：1649-1658）

19 Gao H J，Meng X Y，Chen T W.Stabilization of networked control systems with a new delay characterization. IEEE Transactions on Automatic Control，2008，53（9）：2142-2148

赵国荣海军航空工程学院控制工程系教授.1996年获得哈尔滨工业大学控制科学与工程博士学位.主要研究方向为无线传感器网络，飞行器导航，制导与控制.E-mail:GRZhao6881@163.com

（ZHAOGuo-RongProfessor in the Department of Control Engineering，Naval Aeronautical and Astronautical University.He received his Ph.D.degree in control science and engineering from Harbin Institute of Technology in 1996.His research interest covers wireless sensor networks，aircraft navigation，guidance and control.）

韩 旭海军航空工程学院控制工程系博士研究生.2015年获得海军航空工程学院控制科学与工程硕士学位.主要研究方向为飞行器导航，多传感器信息融合.本文通信作者.

E-mail:hxyy713@163.com

（HAN XuPh.D.candidate in the Department of Control Engineering，Naval Aeronautical and Astronautical University.He received his master degree from Naval Aeronautical and Astronautical University in 2015.His research interest covers aircraft navigation and multi-sensor information fusion.Corresponding author of this paper.）

万兵海军航空工程学院控制工程系工程师.2009年获得海军航空工程学院控制科学与工程硕士学位.主要研究方向为飞行器导航、制导与控制，机器视觉.E-mail:wanbing0908@163.com

（WAN BingEngineer in the Department of Control Engineering，Naval Aeronautical and Astronautical University.He received his master degree from Naval Aeronautical and Astronautical University in 2009.His research interest covers aircraft navigation，guidance and control，and machine vision.）

闫 鑫中国人民解放军91372部队助理工程师.2013年获得海军航空工程学院学士学位.主要研究方向为飞行器导航.E-mail:yanyao618@163.com

（YAN XinAssistant engineer at The Chinese Peaple′s Liberation Army 91372 Troop.He received his bachelor degree from Naval Aeronautical and Astronautical University in 2013.His main research interest is aircraft navigation.）

A Decentralized Fusion Estimator with Stochastic Sensor Gain Degradation，Delays and Data Dropouts

ZHAO Guo-Rong1HAN Xu1WAN Bing1YAN Xin2

The decentralized fusion estimation problem is investigated in the paper for a class of networked uncertain stochastic systems with stochastic sensor gain degradation，data transmission delays，and data dropouts.The model′s uncertainty is described by stochastic parameter perturbations considered in the system matrix.The sensor gain degradation is described by random variable whose probability is assumed to be known.Stochastic delays and data dropouts are considered in the process in which the locally optimal estimates are transmitted to the fusion node.Firstly，a locally optimal estimator is proposed.Then，the data transmission delays are considered to be a stochastic process，and a delaydropout model is put forward to account for the storage mechanism.A decentralized fusion estimator is proposed by minimizing the mean square error on the best linear unbiased estimation（BLUE）criterion.Finally，a simulation example is given to confirm the effectiveness of the proposed approach.

Sensor gain degradation，model′s uncertainty，transmission delay，data dropout，decentralized fusion estimator

10.16383/j.aas.2016.c150320

Zhao Guo-Rong，Han Xu，Wan Bing，Yan Xin.A decentralized fusion estimator with stochastic sensor gain degradation，delays and data dropouts.Acta Automatica Sinica，2016，42（7）:1053-1064

2015-05-20录用日期2016-03-03
Manuscript received May 20，2015；accepted March 3，2016
国家自然科学基金（61473306）资助
Supported by National Natural Science Foundation of China （61473306）
本文责任编委文成林
Recommended by Associate Editor WEN Cheng-Lin
1.海军航空工程学院控制工程系烟台2640012.中国人民解放军91372部队上海200436
1.Department of Control Engineering，Naval Aeronautical and Astronautical University，Yantai 2640012.The Chinese Peaple′s Liberation Army 91372 Troop，Shanghai 200436