混沌变异粒子群算法在水库供水调度规则制定中的应用
韩靓靓
(辽宁省水利水电勘测设计研究院, 辽宁 沈阳 110006)
混沌变异粒子群算法在水库供水调度规则制定中的应用
韩靓靓
(辽宁省水利水电勘测设计研究院, 辽宁 沈阳110006)
【摘要】本文针对基于调度图规则的水库供水调度问题,建立了以水库供水保证率高且缺水量少为目标的优化调度模型。同时应用混沌变异减缓粒子群算法收敛速度,当算法进化停滞步数大于停滞步数阀值时,随机选取其中20%的粒子进行混沌变异操作,将原本聚集的粒子群“驱散开来”,达到增加种群多样性、避免算法早熟收敛的目的,并将该算法引入到调度图的获取中。并以白石水库为例,得到了满足各项用水保证率的水库调度图,验证了该方法的可行性。
【关键词】水库;调度规则;粒子群算法;混沌变异
1 研究背景
水库是水资源系统重要的组成部分,其调度运行与管理的合理性和科学性,决定着水库能否发挥其最大的效益。在不增加工程建设投资的情况下,通过优化水库运行规则,可进一步挖掘水库潜力,增强水库运行的可靠性,提高水库防洪抗旱能力。随着计算机技术及优化算法的进步,水库模拟和优化得到了持续的发展,大多数水库都可以通过模型演算后得到有针对性的调度规则。
目前,水库调度规则模拟作为水资源配置的一个模块,已经嵌入到许多较为成熟的商业软件中,如荷兰代尔夫特水工研究所的RIBASIM、美国陆军工程兵团的HEC-ResSim、丹麦水资源及水环境研究所的MIKE BASIN、中国水科院水资源所的SPWATER等,而水库调度规则的获取仍处在研究阶段。随着智能算法的发展,越来越多的智能算法被引入到水库调度规则获取的领域。Chen[1](1995)、Chang[2](2005)、Shiau[3](2009)等将遗传算法引入到水库供水规则的制定中;张双虎、黄强等[4](2006)在研究乌江水库群优化调度中,采用差分演化算法和遗传算法构建以梯级发电量最大为目标的模型,计算得到梯级水库的最优决策,并给出了梯级总调度图及各水库的优化调度图;尹正杰等[5](2006)以供水调度为例对数据挖掘用于水库调度规则提取进行了研究;王小林等[6](2010)通过协同演化免疫算法提取水库调度规则,黄家文等[7](2011)提出应用判别系数法与水库蓄供水控制线相结合的方法,并结合免疫粒子群算法,对水库蓄供水控制线进行优化。以往学者研究的调度规则中最常见也是最实用的供水调度规则是水库供水调度图,针对调度图的获取形成了一套模拟与优化相结合的混合式方法。笔者在调度图的获取研究中发现,由于粒子群算法本身的缺陷,算法易陷入局部最优,求解过程中需要用较大的粒子数或迭代次数才能得到较优的结果。本文借鉴文献[8]提出了混沌粒子群算法,并将该方法引入水库调度规则研究中。
2 基于调度图的水库供水调度模型
2.1水库供水调度模型供水规则
为便于描述,假设某水库具有三个供水对象(用水户A、用水户B、用水户C),用水户A、用水户B、用水户C供水保证率依次降低。水库调度图如图1所示,根据供水目标的优先级和设计供水保证率高低,限制供水线由下至上依次排列并将兴利库容分成若干调度区。水库运行过程中,根据水库蓄水量所处调度区对应的供水规则(见表1)对每个用水户供水。
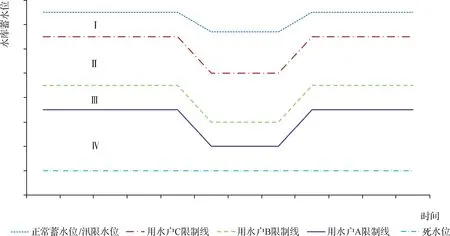
图1 水库调度图示意图

调度图分区用 水 户用水户A用水户B用水户CⅠ正常正常正常Ⅱ正常正常限制Ⅲ正常限制限制Ⅳ限制限制限制限制系数αβη
2.2目标函数
a.缺水量最少。
(1)
(2)
式中T——时段总数;
N——用水户数;
ΔDEi(t)——t时段i用水户缺水量,万m3;
WDi(t)——t时段i用水户需水量,万m3;
WSi(t)——t时段i用水户供水量,万m3。
b.保证率高。
(3)

(4)
(5)
式中Mi(t)——i用水户供水是否满足指标;
Ratioi——i用水户保证率;
Pi——i用水户设计保证率;
其他变量如前文所述。
2.3决策变量
基于调度图的水库供水调度,决策变量本质上为调度图上各控制水位线,据此并结合水库蓄水状态以及限制供水系数确定水库如何供水,概化调度图即为:
(6)
式中n——调度线条数;
m——单条调度线点数;
Xi,j——第i为调度线条数上j点控制水位。
2.4主要约束条件
水库调度模拟模型约束包括水库水量平衡约束、库容上下限约束,在考虑供水情况下还包括供水约束。
a.水库水量平衡约束。

(7)
式中S(t)、S(t+1)——t时段初、末水库库容,万m3;
I(t)——t时段入库水量,万m3;
EC(t)——t时段水库坝下环境需水量,万m3;
SU(t)——t时段弃水量,万m3;
L(t)——t时段水库损失水量,万m3;
其他变量如前文所述。
b.水位约束。
(8)
式中Zmin(t+1)——t时段末水库允许运行的最低水位(死水位),m;
Zmax(t+1)——t时段末水库允许运行的最高水位(汛期为汛限水位,非汛期为正常蓄水位),m。
c.水位库容关系约束。
(9)
式中S(t)——t时段初水库库容,万m3;
Z(t)——t时段初水库水位,m;
A(t)——t时段初水库面积,万m2。
d.供水约束。
(10)
式中αi——i用水户限制供水系数;
其他变量如前文所述。
e.调度线不交叉约束。
(11)
f.非负约束。
式(7)~式(11)中的变量均为非负值。
2.5模型求解
基本粒子群算法前期收敛速度快,但在后期收敛速度变得缓慢,种群中粒子差异变小,种群多样性随迭代次数增加而降低,从而出现强烈的“趋同性”现象,这使粒子群难以摆脱局部极值,这种情况下,如果不采取变异、扰动、分群等措施改变种群现状,增加种群的多样性,则当前粒子群所趋同的那个点即为算法所求的最优解。
本文依据算法进化停滞步数n大于停滞步数阀值N,随机选取其中20%的粒子进行混沌变异操作,这样就可以通过新的变异公式将原本聚集的粒子群“驱散开来”,达到变异的目的,算法流程如图2所示。

图2 混沌变异粒子群算法流程
3 实例研究
3.1水库概况
白石水库位于辽宁省北票市上园乡附近的多沙河流大凌河干流上,坝址以上控制面积17649km2,是一座以防洪、灌溉、城市供水为主,兼顾发电、养鱼的大型水库。水库总库容16.45亿m3。水库原设计正常蓄水位127.00m,防洪限制水位125.60m,死水位108.00m。由于库区移民动迁迟缓原因,水库目前采用的正常蓄水位为120.00m,防洪限制水位为116.00m,死水位为108.00m。水库承担着给阜新市、北票市及义县县城城市生活及工业供水、扇地及下游区间补水、苇田供水的任务。
3.2结果与分析
采用权系数法将保证率大和缺水量小两个目标变为一个目标函数,混沌变异粒子群算法种群规模为300,停滞步数阀值取20,迭代次数取3000次,农业限制供水系数取0.7,工业限制供水系数取0.9。为减少算法的随机性对结果的影响,独立运行10次,选取其中适应度最优结果对应的调度图作为模型求解结果,调度图如图3所示。

图3 白石水库调度图
根据图3所示调度图,模拟水库的运行过程,得到水库的运行参数。水库城市生活及工业供水保证率为95%,扇地及下游区间补水保证率为84%,苇田供水保证率为50%。水库各项供水保证率均满足要求,详见表2。为分析该调度图的有效性,水库分别按该调度图及按需供水的调度规则进行对比,水库供水不存在深度限制甚至中断的情况。
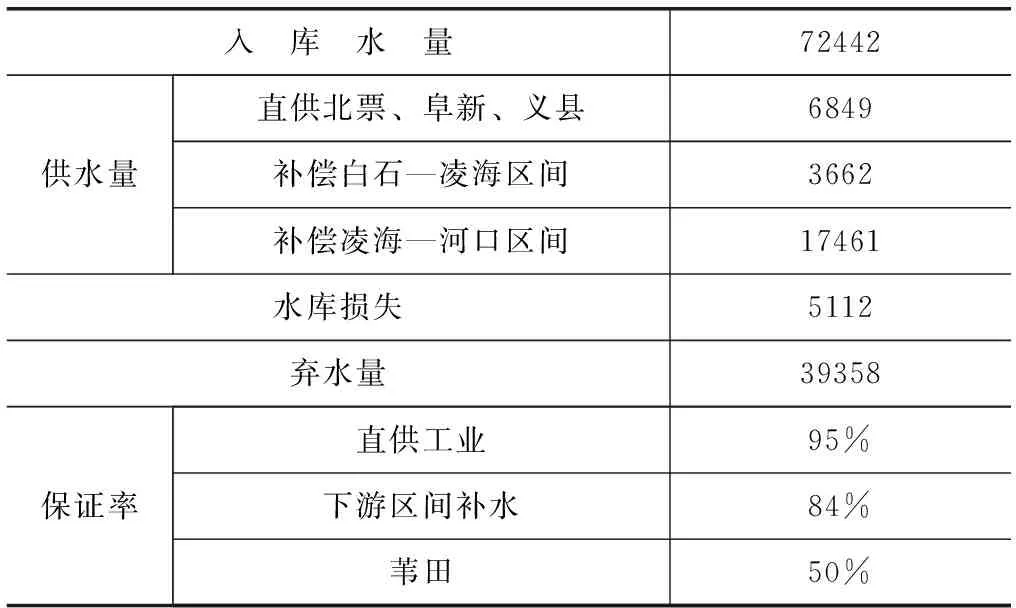
表2 白石水库多年平均运行参数 单位:万m3
4 结 语
本文针对水库供水调度问题,引入混沌变异粒子群算法,建立基于模拟优化方法的水库调度图优化模型,将该模型应用到白石水库调度图求解中,水库按求解得到的调度图运行,水库各项供水保证率都满足要求,且不存在深度缺水问题。本研究为白石水库的调度运行提供了科学的依据,也为水库调度图的获取提供了新的参考。
参考文献
[1]Chen L.A study of optimizing the rule curve of reservoir using object oriented geneticalgorithms [D].Taipei:Desect1ment of Agricultural Engineering, National Taiwan University,1995.
[2]Chang F J,Chen L,Chang L C.Optimizing the reservoir operating rule curves by genetic algorithms [J].Hydrological Processes,2005(19):2277-2289.
[3]Shiau J.Optimization of reservoir hedging rules using multiobjective genetic algorithm [J].Water Resource Planning and Management.2009,135(5),355-363.
[4]张双虎,黄强,黄文政,等.基于模拟遗传混合算法的梯级水库优化调度图制定[J].西安理工大学学报,2006,22(3):229-233.
[5]尹正杰,王小林,胡铁松,等.基于数据挖掘的水库供水调度规则提取[J].系统工程理论与实践,2006(8):129-135.
[6]王小林,成金华,尹正杰,等.协同演化免疫算法提取水库调度规则研究[J].中山大学学报,2010,49(6):121-125.
[7]黄家文,胡滢,李华穂.梯级水库联合优化调度模型及其应用[J].中国水能及电气化,2011(12):11-16.
[8]高尚,杨静宇.混沌粒子群优化算法研究[J].模式识别与人工智能,2006,19(2):266-270.
DOI:10.16617/j.cnki.11-5543/TK.2016.07.016
中图分类号:TV697.1
文献标识码:A
文章编号:1673-8241(2016)07- 0049- 05
Application of chaotic variation sect1icle swarm optimization in reservoir water supply dispatching rules making
HAN Liangliang
(LiaoningWaterResourcesandHydropowerSurveyDesignInstitute,Shenyang110006,China)
Abstract:In the paper, optimization dispatching model with high reservoir water supply guarantee rate and less water deficiency variation as targets is established aiming at reservoir water supply dispatching problems based on dispatching chart rules. Meanwhile, the convergence rate of sect1icle swarm optimization algorithm is slowed down by applying chaotic variation. When algorithm evolutionary stagnation steps are greater than stagnation step threshold, 20% sect1icles thereof are randomly selected for chaotic variation operation. The originally gathered sect1icle swarms are ‘dispersed’ to reach the purposes of increasing population diversity and avoiding premature convergence. The algorithm is introduced into the dispatching chart acquisition. Baishi Reservoir is adopted as an example for obtaining the reservoir dispatching chart meeting all water consumption guarantee rates. The feasibility of the method is verified.
Key words:reservoir; dispatching rules; sect1icle swarm algorithm; chaotic variation

