贵州省贵阳市城镇居民消费与支出分析
唐佳宁


摘要:用EViews软件建立贵州省贵阳市居民消费支出与人均可支配收入的模型,并对模型使用软件进行分析与预测。
关键词:EViews软件;回归;JB检验;线性
一、Eviews软件简介
Econometics Views 被通常被简写为Eviews,被用通俗的话语解释为激励经济学,或有时被称为计量经济学软件包.应用Eviews软件的解决生活中数据的统计,并得出之间的关系。进而预测其可能出现的情况。
二、收集数据
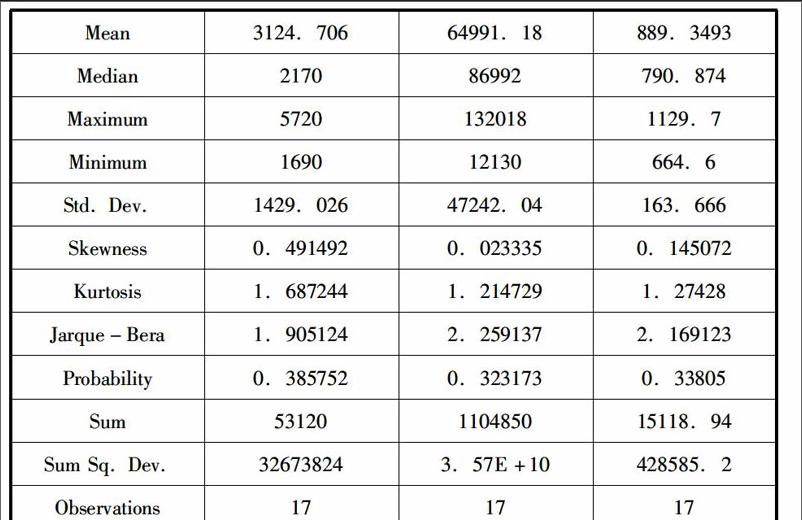
以下的数据显示的是贵州省贵阳市1998-2014年城市和其周围由贵阳市所管辖的乡镇的人民每个人的花费的支出以及每个人的可以由自己支配的收入。
三、研究数据关系以及涉及建立模型
首先,建立数学模型可以有很多类型,人们通常的判断方法是通过先根据数据的分布规律找到散点图,如下展示的是散点图:图1
图1我们所知道的线性模型所表示出的散点图规律来看,上图中贵州省贵阳市城镇居民每个人的花费的支出以及每个人的可以由自己支配的收入所形成的散点图显示的就是线性模型,并且由图来看显示的是一元线性模型。根据前人的经验来看,最小二乘法是被用来对一元线性进行回归的,而且对一元线性进行回归的最小二乘法有一些基本假设的要求,这些基本的假设要求中的一个就是,随机干扰项U通常情况下被认为是非负态的,根据前面科学家的指导来看我们要应用μi的近似值—残差ei来检验ui的正态性. 这样做得真正原因是我们直接的了解不到非假设性的ui(误差项)。通常我们应用的是被简称为JB检验的雅克-贝拉(Jarque-Bera)正态性检验.雅克-贝拉检验通常通过对本文数据(大样本)的一种检验方法,通过最小二乘法的残差,对本文数据模型进行检验,有时被称为渐进检验,于是Jarque和Bera建立了下面的检验统计量———JB统计量。
JB=n6S2+(K-3)24(2)
在这之中,我们通常称S被称为偏度,同样N被称为样本容量。
K=∑(Xi-X)4nσ4X
通常情况下K被称为峰度, 与此同时上面假定印证了非负态假定,正如(2)式所说慢慢地附和x2等于3的自由度的雅克-贝拉检验,通常的表示方式为X2(3)。通过观察上面的式子了解到,假设正态分布的假设被服从,因此得到的s=0、k等于3。我们通过以上结论得出的雅克-贝拉统计数量是0.不过如果假设我们假设认为次变量是负态变量,我们就应因此得出结论为我们的统计量的值是越来越大的,正因如此,我们就会算出雅克-贝拉统计量,并且我们要借助x平方分布所显示值来计算。通过给定的显著性水平a=0.006,查出x2(2)=5.88189。我们假设这其中的二式通过计算所得出的结论大大的越过了分界点χ2(2)= 5.88189,我们就说它是否定了正态分布;如果结论反之就证明了原假设。.
因此有JB=6.2.672345小于X2(3)等于6.3,这其中显示出了我们所得到的统计的数量是统计非显著的.所以我们结论能否定非零假设:贵阳市城市和乡镇的人民支出回归的残差和正态分布是一致的.所以就体现了我们最小二乘法的检验,通过使用Eviwes统计软件做回归,结论我们通过应用软件所拥有的结论得出 I等于45.456+0.25678,S=135.0013(0.05629)
T=(5.3204)(456.789)R2等于1.3420 F等于26458.945
四、模型检验和预测
(一)标准差误差的评价估计
通常我们所说的样本回归线和样本观测值相互的的拟合度之间的大小被称为拟合优度,通常用来显示的量为非不可决系数的大小,通常我们用来了解解释变量相对于被解释的解释的程度的大小。在文中所使用的假设模型中,R2=0.134,通过数据充分体现了文中数据的反应相关关系的作用,充分展示出贵阳市城市和其管辖的县区人民的最末尾购买性的花费Yi的变量中,有解释变量城镇居民人均可支配收入解释的部分占99.93%,我们所应用的一元线性模型的相关度较高。
(二)一元线性的显著性检验
通过统计量β1,t的数值为156点332,已经确定了的a=0.063,通过对比t的统计分布表,由于在自由度是n-2=19的条件下,我们所得出的转折点为t0.35(13)=2.134,因为t=172。325大于统计量t0.036(18)=2.045,所以H等于0;β1=0,通过以上数据显示出了贵阳市的人民收入可以花销的部分相对于居民花费所消耗掉的部分有着很显著的影响。
(三)对一元线性统计进行预测
我们通过Eviews统计学软件计算出了在我们数据所在的年份里被解释变量数值的拟合值,我们的拟合值标记为YF,其拟合值和实际生活中的值的比较如下图所示:
(作者单位:贵州大学)
参考文献:
[1]李子奈.计量经济学[M].北京:高等教育出版社,1996.
[2]平狄克,鲁宾费尔德.微观经济学[M].北京:中国人民大学出版社,1996.

