花键传动杆偏心的可靠性影响分析

翟振强

（哈尔滨东安发动机（集团）有限公司 黑龙江哈尔滨 150066）

花键传动杆偏心的可靠性影响分析

翟振强

（哈尔滨东安发动机（集团）有限公司 黑龙江哈尔滨 150066）

传动杆是附件传动系统中重要构件之一，从发动机中央传动至附件传动机匣连接的传动杆称主传动杆，国外称塔轴。传动杆属于轴类零件，特点是长径比大，两端皆有渐开线花键。靠花键与功率输入、输出轴相连。花键联接中常采用各种不同的定心方式以提高轴与轮毂的同心度，如外径定心、内径定心或齿形定心。但无论采用哪种定心方式都很难保证轴与轮毂的绝对同心。轻则造成花键齿啮合不好，产生冲击和噪声；重则出现啮合产生“抱齿”现象，造成重大质量事故。所以认识花键传动杆偏心对传动系统的影响有着重大意义。本文同过对花键传动杆偏心的可靠性影响分析，认识花键传动杆偏心对传动系统的影响。

花键；传动；杆偏心

1 花键传动杆偏心引起摩擦损失

当花键正常工作时，载荷均匀的分布在每个键齿上。当花键偏心时，花键在配合齿形面上呈三角形接触，只有最远处的齿才处于接触状态，啮合数量很少，这时花键啮合时的工作状态类似于内啮合传动的齿轮，载荷全部施加在这两个齿上，且延齿长方向分布不均。

啮合的轮齿齿廓间存在相对滑动。如图1，设构件以等角速度ωH绕O2顺时针转动，它与平动机构一起为平动花键1提供平移运动，通过平动花键1与花键2的啮合，将运动和动力输出。设花键2角速度为ω2，在图示位置，主、从动齿轮上两齿廓E1、E2在K点啮合，则K点必定落在两基圆公切线（即过K点的两齿廓的公法线）PN2上。此时，齿廓E1、E2上K点的速度分别为：

Vk1=ωHα′方向垂直于 O1O2；

Vk2=ω2rk2方向垂直于O2K；

二者在过K点的齿廓公切线t-t上的分速度分别为：

因为花键1平动，所以Vk1始终垂直于两轮的连心O1O2，因此，Vk1与公法线间的夹角始终等于啮合角α′，所以Vk1的大小始终不变。

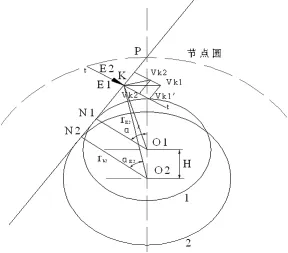
图1 齿间相对滑动

由于此时两齿廓在啮合点K处沿齿廓公切线的分速度不相等，所以，两齿廓沿公切线方向必然有相对滑动速度存在。设相对滑动速度为Vs，则：

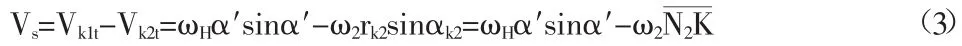
由运动关系可知：外齿轮平动时，该平动机构的传动比为：

由该式可知：在啮合时，齿廓间的相对滑动速度大小与PK有关，而PN1、PN2是恒定不变的，所以，K点的位置决定了相对滑动速度的大小。

对花键机构，由于进入啮合时，是由1的齿顶推动2的齿根部分开始的，所以开始时，K点距节点P最近，即PK最小，因此，此时的相对滑动速度也最小；而退出啮合时，是由1的齿根部分推动2的齿顶，所以退出啮合时K点距节点P最远，即PK最大，因此，此时的相对滑动速度也最大。

当存在偏心的轴毂连接工作时，各齿啮合的松紧程度必不相同，图1所示，啮合点K在啮合过程中，沿PN1向P点靠近，这时α′大小不变，αa2增大，摩擦损失增大。相互摩擦，每转一周，摩擦重复一次。

2 花键传动杆偏心对联接强度的影响

花键联接的受力情况，其主要的失效形式是工作面被压溃（静联接）或工作面过度磨损（动联接）。静联接按工作面上的挤压应力进行强度计算时，假设载荷在键的工作面上均匀分布，每个齿工作面上的压力的合力F作用在平均直径dm处，即传递的转矩T=F×dm/2，并引入系数ψ来考虑实际载荷在各花键齿上分配不均的影响，花键联接的强度条件为：

式中：ψ——载荷分布不均系数，与齿数多少有关，一般取ψ=0.7～0.8，齿数多时取偏小值；

z——花键的齿数；

h——花键齿侧的工作高度，渐开线花键，α=30°，h=m；α=45°，h=0.8m，m为模数；

dm——花键的平均直径，渐开线花键，dm=di，di为分度圆直径，单位为mm；

[σp]——花键联接的许用挤压应力，单位为MPa；

[p]——花键联接的许用压力，单位为MPa。

式中ψ-载荷分布不均系数，与齿数多少有关，一般取ψ=0.7～0.8，齿数多时取偏小值。当花键偏心工作时，花键在配合齿形面上呈三角形接触，载荷全部施加在这两个齿上，且延齿长方向分布不均，啮合紧密的键齿将承受较大的压力。这时，工作面上的压力增大，载荷分布不均系数ψ增大，静载荷和动载荷也随之增大。

3 花键传动杆偏心对键齿润滑的影响

在花键传动高副接触中，两摩擦表面之间接触压力很大，摩擦表面会出现不能忽略的局部弹性变形。同时，在较高压力下，润滑剂的粘度也将随压力发生变化。

在弹性流体动力润滑条件下，接触面的弹性变形、油膜厚度及油膜压力分布。靠润滑剂与摩擦表面的粘附作用，两圆柱体相互滚动时将润滑剂带入间隙。由于接触压力较高使接触面发生局部弹性变形，接触面积扩大，在接触面间形成了一个平行的缝隙，在出油口处的接触面边缘出现了使间隙变小的突起部分（一种缩颈现象），并形成最小油膜厚度，出现了一个第二峰值压力。当花键传动杆偏心时，内啮合键齿的节点靠近齿根处是油膜厚度的最薄弱处，且在变速传动时，低速传动的内啮合工况润滑状态较差。

4 结论及改进措施

由于造成花键齿几何偏心的最主要原因是滚齿装夹定位误差和热处理变形，因此，对于精度要求高的花键齿，以进一步提高滚齿时的装夹定位精度。

[1]张春林，姚九成.平动齿轮机构连续传动条件的分析方法.机械科学与技术，1998.

[2]饶振刚.行星传动机构设计（第二版）.北京：国防工业出版社，1994.

TH131

A

1004-7344（2016）02-0236-02

2015-12-22