战术导弹三自由度弹道仿真模型研究

张安民,　崔连虎,　赵世明

(中国人民解放军91336部队,河北 秦皇岛　066000)



战术导弹三自由度弹道仿真模型研究

张安民,崔连虎,赵世明

(中国人民解放军91336部队,河北 秦皇岛066000)

摘要：针对弹道仿真模型逼真度和情报资料欠缺之间的矛盾,通过一系列假设条件和近似处理,分别对弹体动力学/运动学、制导控制系统、弹目信息解算等模型进行合理简化,实现了从高精度六自由度弹道模型到三自由度质点弹道模型的转化。对比分析同一非机动、机动目标态势下的仿真结果,验证了简化模型与原模型弹道特性的一致性。简化模型辅以必要的情报参数,可以逼真描述一类战术导弹的战场行为特性,满足了诸多作战仿真推演、演习训练、视景仿真等工程应用需求。

关键词：战术导弹; 三自由度; 制导控制系统; Simulink; 一致性

1引言

建模与仿真技术广泛应用于战术导弹的论证、研制、试验、鉴定、作战使用和训练的各个环节,不同应用需求催生了多种不同层次的弹道仿真模型[1-3]。其中,六自由度弹道模型逼真度最高,可以精确描述制导控制系统作用下的导弹动力学/运动学特性,适用于战术导弹的研制及试验过程;而在作战仿真推演、演习训练、视景仿真等应用场合,受限于模型获取渠道、模型运算量等因素,往往选择简化的位置递推模型描述导弹运动轨迹。这种简化模型描述能力有限,模型逼真度较低,直接影响仿真推演结果的可信度、仿真训练的效果,限制了仿真技术在军事应用中的快速发展。

在具备高逼真度六自由度弹道仿真模型的前提下,通过设定一系列假设条件,可以将模型简化为三自由度质点运动模型[4,5],既可保留对质心弹道和制导控制规律的描述能力,又可降低对建模对象情报参数的依赖程度,从而满足作战仿真推演、演习训练等弹道仿真模型需求。本文以某六自由度弹道仿真模型为基础,研究可行的模型简化方法,建立三自由度弹道仿真模型,并对比分析简化三自由度模型与原六自由度模型的一致性,验证简化模型的正确性。

2六自由度弹道仿真模型

一个完整的寻的制导弹道仿真模型主要包括弹体动力学/运动学模型、自动驾驶仪模型、导引头模型和制导指令生成模型等。为了实现闭环运行,在仿真系统中通常还需要目标运动模型和弹目相对运动模型。此外,还可根据需要增加干扰噪声模型和误差模型[6]。模型总体框架如图1所示。

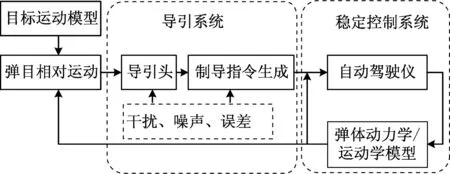
图1　寻的制导弹道仿真模型总体框图Fig.1　The diagram of homing guidance trajectory simulation model

从控制系统角度来看,弹道仿真模型可划分为导引系统和稳定控制系统。弹体作为被控对象与自动驾驶仪构成姿态稳定控制回路,实现干扰条件下导弹的稳定飞行,同时在导引系统的控制作用下沿指定弹道飞向目标。

(1) 弹体动力学/运动学模型

导弹在空间运动一般看成可控制的变质量系统具有六个自由度的运动,即姿态运动和质心运动。利用“固化原理”,通常把导弹作为常质量刚体,建立动力学方程、运动学方程和几何关系方程,构成六自由度弹体模型,详细内容请参见文献[4,5]。

(2) 自动驾驶仪[7]

自动驾驶仪模型描述了制导控制指令、伺服传动和弹体运动之间的交互关系,其功能是控制与稳定导弹飞行。常用的双通道控制方式中,导弹的横向机动控制分解到俯仰和偏航两个通道中进行。对于滚转通道,仅对其进行稳定,而不进行控制。

(3) 导引头

导引头是导弹上的目标信息敏感装置,其功能是捕捉跟踪目标,并输出实现导引律所需要的信息。导引头模型应该正确描述目标捕捉跟踪范围、跟踪精度、伺服响应特性等,并具备制导信息滤波功能。

(4) 制导指令模型

制导指令模型用于接收导引头目标检测信息,并将其与导弹运动信息综合形成导引误差,按照预定的导引规律生成制导指令,通过自动驾驶仪控制导弹跟踪直至命中目标。比例导引法是常用的寻的制导导引律。

上述模型按信息交互关系相互连接,即可实现对导弹制导飞行过程的六自由度逼真模拟。

3弹体模型简化

除导弹研制与试验等应用场合以外,多数仿真系统期望能够简捷地得到导弹可能的飞行弹道及其主要飞行特性,并不太关心导弹的飞行姿态。因此,可以将导弹当作一个可操纵质点,省略绕质心转动方程,建立三自由度质点弹道模型。

3.1模型简化假设条件

3.1.1“瞬时平衡”假设

对于操纵性能好、绕质心运动不太激烈的轴对称导弹,可采用“瞬时平衡”假设,即[4,5]:

(1) 导弹绕弹体轴的转动是无惯性的;

(2) 稳定控制系统理想工作,无误差,无时间延迟;

(3) 略去随机干扰对法向力的影响。

由此可以认为导弹时时处于力矩平衡状态。根据力矩平衡关系,可以省略力矩计算相关方程组,直接计算得到与舵偏角相对应的平衡攻角和侧滑角。

3.1.2“速度倾斜角为零”假设

对于非滚转导弹,在攻角、侧滑角不大的前提下,速度倾斜角一般在零度附近。在不会给弹道特性造成明显影响前提下,为了处理方便,可以将其假设为零。

为了验证这一假设的可行性,分析六自由度弹道仿真模型速度倾斜角变化曲线,并通过强制赋值为零方式研究弹道特性的变化。设置仿真态势:目标蛇形机动,飞行速度约1马赫,机动过载10g;导弹飞行速度约3马赫,最大可用机动过载40g;弹目初始距离约9.7km。仿真结果如图2所示。

图2　速度倾斜角及相应弹道误差曲线Fig.2　Velocity angle and Ballistic error curve

分析典型仿真试验结果可知,在目标机动不大(速度约1马赫,过载不超过10g)态势下,导弹攻角、侧滑角在10°左右范围内变化;而速度倾斜角大部分时间较小(小于1°),在弹道末段出现幅度约为4°的快速变化,仍在0°附近(图2a)。将速度倾斜角强制置零,在闭环仿真过程中仅带来米级的弹道曲线偏差,并且这一偏差随着弹目距离逼近而迅速减小,不会给脱靶量带来明显偏差(图2b)。因此,“速度倾斜角为零”的假设条件具有现实可行性。

3.2三自由度质点弹道模型

基于上述简化,可以把导弹的质心运动和绕质心转动运动分开研究。于是可将六自由度弹体模型简化为如下方程组

(1)

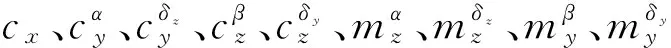
4自动驾驶仪模型简化

自动驾驶仪是一个典型的稳定控制系统,按功能可划分为敏感元件、弹上计算机模块和执行机构模块[7]。敏感元件敏感导弹姿态、加速度信息,送至弹上计算机模块计算控制量的大小,最后通过执行机构(舵系统)改变导弹运动状态,实现导弹的稳定飞行。

为了适应三自由度弹体模型,对自动驾驶仪模型做如下简化处理:

(1) 敏感元件仅输出弹道坐标系下的加速度。根据“瞬时平衡”假设,不需要对弹体姿态进行稳定控制,因此也就不需要测量弹体姿态角、角速度信息,仅保留加速度信息。同样由于缺少导弹姿态信息,加速度信息只能基于弹道坐标系。作为模型,这一假设具有可操作性。

(2) 保留俯仰、方位双通道控制结构,简化控制系统传递函数。自动驾驶仪对制导指令的响应特性直接影响弹道特性,不宜进行理想化处理。为此,可以保留双通道控制结构,省略速率反馈等阻尼回路,仅简化为一个随马赫数、攻角/侧滑角变化的增益调度一阶限幅控制回路,输入量为加速度误差信号,输出量为舵系统控制信号。以俯仰控制回路为例,图3给出了控制系统结构图。

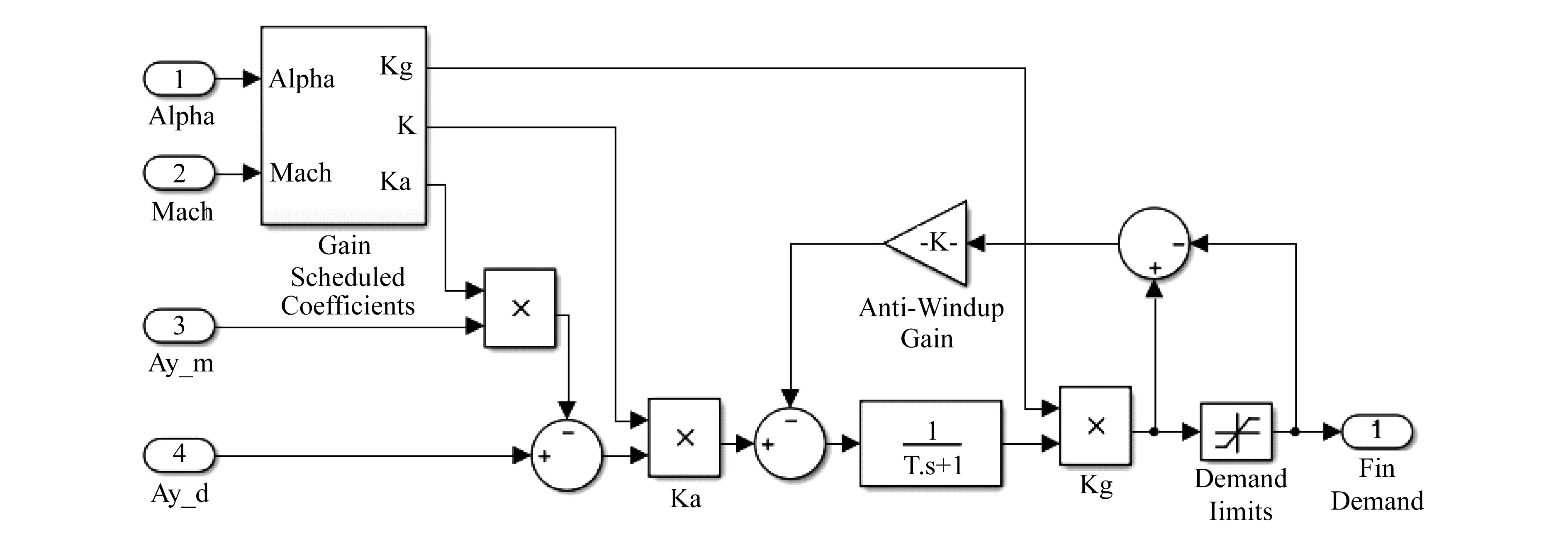
图3　俯仰通道加速度跟随控制系统结构图Fig.3　The diagram of acceleration tracking control system for pitch channel

(3) 舵系统简化为一个二阶限幅控制回路。其传递函数可表示为

(2)

式中,ωn表示自然频率,ξ表示阻尼比。合理调整两个参数,可以较为逼真地描述舵系统的响应特性。

5导引系统模型简化

导引系统模型包括导引头模型和导引律模型两部分。

5.1比例导引模型

导引律模型形式较为简单,不做进一步的简化。但工程上实现比例导引一般需要对导引头检测信息进行滤波处理(如:卡尔曼滤波等),这里简化为一个一阶滤波环节,比例导引方法的实现模型[6]为

(3)

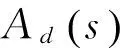
5.2导引头模型

导引头模型用于描述导弹的目标捕获能力、目标信息检测能力和伺服响应特性。对模型做如下简化处理:

(1) 目标捕获能力由导引头作用距离、角度搜索范围等性能指标进行描述,目标进入该范围内即可捕获目标。目标搜索过程用一个延时环节模拟,其余部分作理想化处理。

(2) 目标检测信息基于弹道坐标系。与自动驾驶仪中的加速度检测信息处理相类似,这里的弹目相对运动信息解算同样基于弹道坐标系进行。该假设与自动驾驶仪相呼应,恰好解决了导弹加速度控制过程中的控制量和实测量的匹配问题,后续仿真实践证明了这一假设的合理性和可行性。

(3) 伺服响应特性简化为一阶控制回路。在导引头跟踪目标过程中,伺服响应特性可采用通用的导引头数学模型进行如下描述

(4)

式中,q(s)为目标视线角,T2为导引头时间常数。

6三自由度弹道仿真模型性能分析

在MATLAB/Simulink环境下实现上述简化模型,增加目标运动及弹目相对运动模型,即可开展导弹追踪目标的仿真研究,仿真模型总体结构如图4所示。

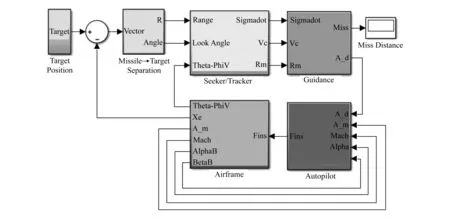
图4　Simulink简化弹道仿真模型结构图Fig.4　The diagram of trajectory simulation model by simulink

为了分析三自由度简化模型与原六自由度模型的一致性,在Simulink环境下设置相同目标态势,对比分析两个模型的弹道轨迹和过载控制曲线。

6.1非机动目标态势下的分析验证

态势1:目标匀速直线运动,速度1马赫;导弹初始速度3马赫;弹目初始距离约为5.7 km。

可见,导弹以3马赫速度攻击速度为1马赫的非机动目标时,三自由度简化弹道和原六自由度弹道基本重合(图a),每一时刻的导弹位置偏差不超过5米(图c)。追踪过程中,两个模型的实际横向过载变化趋势一致,大小略有偏差。

6.2机动目标态势下的分析验证

态势2:目标蛇形机动,飞行速度约1马赫,机动过载10g;导弹飞行速度约3马赫,最大可用机动过载40g;弹目初始距离约为9.7km。

可见,追踪横向过载为10 g的机动目标,两个模型所得弹道轨迹偏差略有增大,但在接近目标的飞行末段,偏差仍能控制在较小的范围内(2 m);导弹横向过载曲线仍具有一致的变化趋势。由于初始弹目距离较“态势1”更远,使得最大横向过载不大;但由于目标机动,使得在接近目标的飞行末段,导弹付出了较大的横向过载(约为20 g)。

综合上述仿真试验结果,三自由度简化弹道模型能够一致地模拟原六自由度弹道模型的弹道特性、过载变化特性等;跟踪过程中弹道偏差不大,最终的脱靶量偏差可以控制到0～2 m范围内,验证了模型简化的可行性。

图5　目标匀速直线运动态势下仿真结果对比图Fig.5　The results under the situation of uniform linear target motion

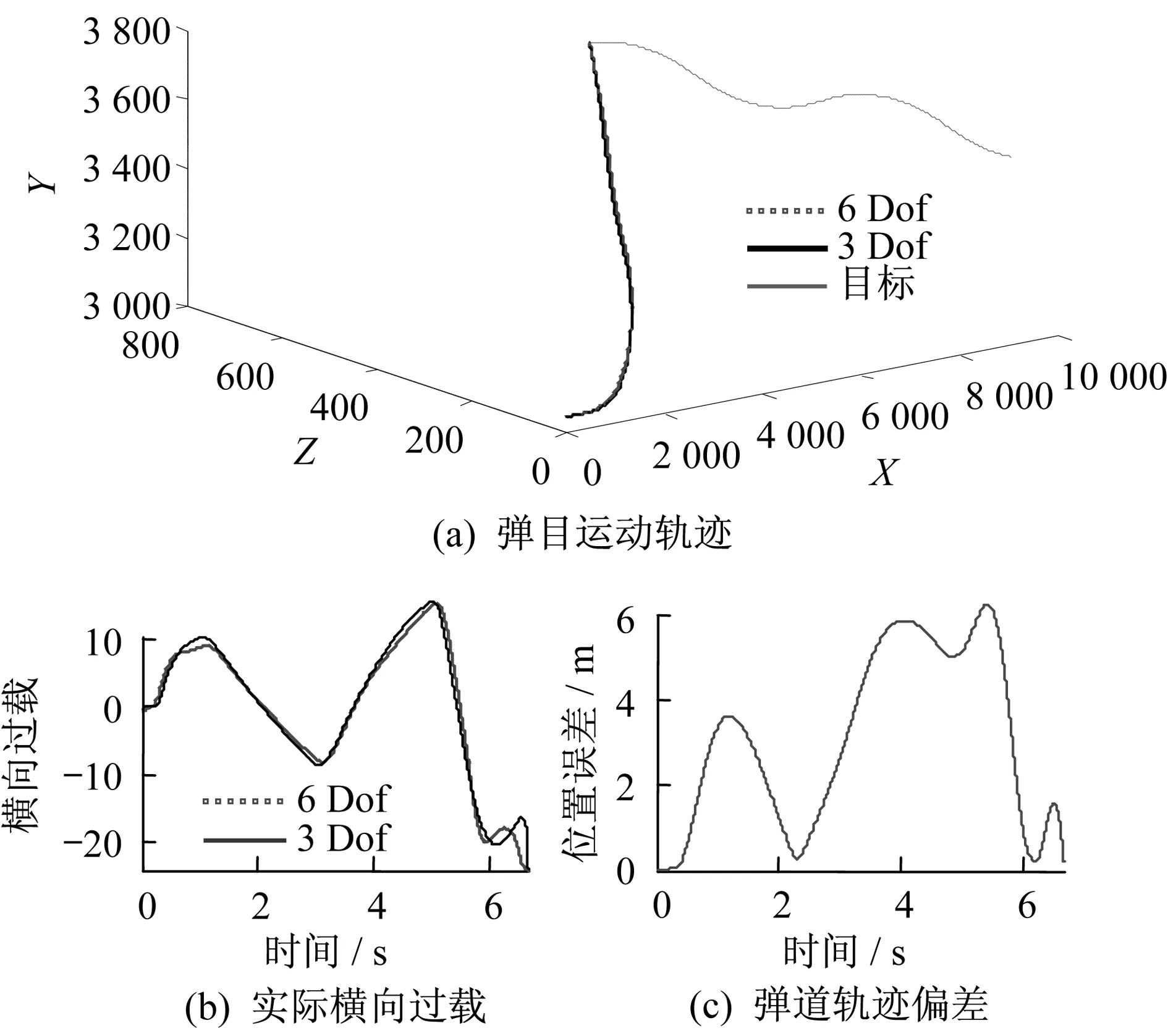
图6　目标蛇形机动态势下仿真结果对比图Fig.6　The results under the situation of S maneuver target motion

7结论

通过一系列假设和简化处理,实现了由高精度六自由度弹道模型到三自由度质点弹道模型的转化,对比分析验证了简化模型的正确性和可行性。三自由度简化弹道模型既可以作为通用弹道模型,辅以必要的情报参数,在作战仿真推演应用中描述各战术导弹(包括敌我双方)的战场行为特性;同时,对于如视景仿真等需要在一定程度上描述导弹姿态的应用环境,可以利用模型中的平衡攻角、侧滑角代替俯仰角和偏航角,进行可接受的近似处理,满足仿真训练的需求。通过通用模型和必要的情报参数来描述一类导弹的战场行为特性,可以有效缓解模型逼真度和情报资料欠缺之间的矛盾,解决工程实践中的现实问题。

参考文献:

[1]王婷,周军.PAC-3拦截弹建模与仿真研究[J].系统仿真学报,2007,19(20):4642-4645.

WANG Ting,ZHOU Jun.Modeling and Simulation Research of PAC-3 Interceptor[J].Journal of System Simulation,2007,19(20):4642-4645.

[2]朱永文.对抗仿真系统中的防空导弹比例导引法仿真弹道设计[J].系统仿真学报,2005,17(12):3095-3097.

ZHU Yongwen.Proportional Navigation Trajectory Simulation In Air Defence System[J].Journal of System Simulation,2005,17(12):3095-3097.

[3]顾浩等.典型反舰导弹运动建模与仿真技术[J].系统仿真学报,2006,18(8):2067-2069.

GU Hao.Typical Anti-vessel Missile′s Motion Modeling and Simulation Technology[J].Journal of System Simulation,2006,18(8):2067-2069.

[4]钱杏芳.导弹飞行力学[M].北京:北京理工大学出版社,2008.

QIAN Xingfang.missile flight aerodynamics[M].Beijing:Beijing Institute of Technology Press,2008.

[5]李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2008.

LI Xinguo,FANG Qun.Winged missile flight dynamics[M].Xi′an:Northwestern Polytechnical University Press,2008.

[6]刘兴堂.导弹制导控制系统分析、设计与仿真[M].西安:西北工业大学出版社,2006.

LIU Xingtang.The missile guidance control system analysis and design and simulation[M].Xi′an:Northwestern Polytechnical University Press,2006.

[7]彭冠一.防空导弹武器制导控制系统设计(上)[M].北京:宇航出版社,1996.

PENG Guanyi.Air defense missile weapon guidance control system design(volume one)[M].Beijing:Aerospace press,1996.

张安民男(1977-),河北滦县人,高工,主要研究方向为电子对抗系统仿真

崔连虎男(1983-),河北邢台人,硕士,工程师,主要研究方向为导弹武器系统仿真。

中图分类号：TP 391.9

文献标识码：A

Study of three Degree of Freedom Tactical Missile Simulation Model

ZHANG Anmin,CUI Lianhu,ZHAO Shiming

(No.91336 Troop of PLA,Qinhuangdao 066000,China)

Abstract：Aiming at the contradiction between fidelity of missile model and intelligence information lack,through a series of assumptions and approximations,the missile dynamics / kinematics,guidance and control system,and the missile-target relative motion model is simplified respectively,high precision of six degree of freedom trajectory model was simplified as three degree of freedom trajectory model.Comparative analysis of simulation results with a non-maneuvering,maneuvering target situation,verify the ballistic characteristics consistent with the original model and simplified model.The results of application show that,it can improve the efficiency of 1 times the solution simplified model method.The simplified model with the necessary information parameters can describe a class of tactical missile realistic battlefield behavior features,and meets the combat simulation,training exercise,visual simulation requirements.

Key words：tactical missile; three degrees of freedom; control and guidance system; simulink; consistency