带积分边界条件的四阶常微分方程边值问题
谭启军(重庆房地产职业学院,重庆 401331)
带积分边界条件的四阶常微分方程边值问题
谭启军
(重庆房地产职业学院,重庆 401331)
摘要:本文应用不动点定理研究一类非局部四阶边值问题正解的存在性和非存在性[1].以往大部分文章中的四阶问题边值条件是局部的,本文研究含有一个系数的非局部边值问题正解的存在性和非存在性.
关键词:边值问题;积分边界条件;不动点定理;正解;四阶常微分方程
0 引言
本文研究如下边值问题:

其中,ω在t=0和(或者)t=1处奇异[2],f∈C[0,1]×[0,+∞)×(-∞,0],[0,+∞)],g,h∈L1[0,1]非负.
假设满足如下条件:

(H2)f∈C([0,1]×[0,+∞)×(-∞,0],[0,+∞));
(H3)g,h∈L1[0,1]非负,μ∈[0,a),v∈[0,a).其中

J=[0,1],E∈C2[0,1].

显然,(E,||x||2)是一个Banach空间,简记为E.
令K是E中的锥,
Kr={x∈K∶||x||2≤r},鄣Kr={x∈K∶||x||2=r},Kr,R={x∈K∶r<||x||2≤R}.
其中,0 引理1假设条件(H0)和(H3)成立,且μ≠a,v≠a.则对任意的y∈C[0,1],x是如下边值问题的解: 当且仅当 其中 其中σ=a2+2abτ. 1.1首先证明必要性 令z=x''则边值问题(2)可变为 上式通过反复计算可得 类似地,由 得 类似地,式(8)代入式(9)得 因此,必要性已证. 1.2下证充分性 根据H1的定义以及式(10),z(s)是如下边值问题的解: 类似地,式(11)蕴含着x(t)是如下边值问题的解 由(12)以及(13)式,充分性得证. 命题1假设条件(H0)和(H3)成立,且μ≠a,v≠a。则有 在E中构造锥K: 易知K是E的闭凸锥,且 定义算子T∶C2[0,1]→C2[0,1]∶ 记 由式(20)可知H(t,s)有如下性质. 命题2假设条件(H0)和(H3)成立,且μ≠a,v≠a.有 引理2假设条件(H0)-(H3)成立.如果x∈C2[0,1]积分方程 引理3假设条件(H0)-(H3)成立.则T(k)∪K且T∶K→K全连续. 下面给出几个记号 其中β表示0或者∞,且 定理1Ω1和Ω2是实Banach空间E中的有界开集,,P是E中的锥,全连续.如果下列条件满足 定理2假设条件(H0)-(H3)成立.边值问题(1)至少有一个正解[3],当且仅当下列条件之一成立 其中,λF(f0+ε1)≤1 这意味着 其中ε2>0,满足(f0-ε2)∧≥1 因此 这意味着 定理3假设条件(H0)-(H3)成立,且则边值问题(1)没有正解. 证明假定x是边值问题(1)的一个正解,则对任意0≤t<1得x∈K,x(t)>0 并且 因此,对任意t∈J,x∈K,x(t)>0得 这是一个矛盾[6].故定理成立. 类似地,可得出以下结论: 定理4假设条件(H0)-(H3)成立,且λ∧f(t,x,y)>|x|+|y|,坌t∈J,坌|x|+|y|>0 则边值问题(1)没有正解. 此定理的证明类似于定理(26)的证明,故证明细节省掉. 参考文献: [1]马如云.非线性常微分方程非局部问题[M].北京:科学出版社,2004. [2]冯美强,张学梅,葛渭高.四阶微分方程奇异边值问题的正解[J].应用数学学报,30(2007)452-461. [3]李永祥.四阶非线性边值问题解得存在性与上下解解法[J].数学物理学报,2003(23):245-252. [4]郭大钧,孙经先,刘兆理.非线性常微分方程泛函方法[M].济南:山东科学出版社,2005. [5]李永祥.四阶边值问题正解的存在性和多解性[J].应用数学学报,2003(26):109-116. [6]葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007. 责任编辑李燕 中图分类号:O175 文献标识码:A 文章编号:1674-5787(2016)01-0141-06 DOI:10.13887/j.cnki.jccee.2016(1).40 收稿日期:2015-11-12 作者简介:谭启军(1987—),男,重庆房地产职业学院,助教,研究方向为数学建模。 Boundary Value Problems of Fourth-Order Ordinary Differential Equations with Integral Boundary Conditions TAN Qijun Abstract:The author uses the fixed point theorem to study existence and non-existence of positive solutions for a class of non-local fourth-order boundary value problems.In the past,the fourth order boundary problem value conditions are partial in most of the articles,but this paper contains a coefficient’s nonlocal boundary value problem’s positive solution existence and non-existence. Keywords:boundary value problem;integral boundary condition;fixed point theorem;positive solution; fourth order ordinary differential equation1 预备知识














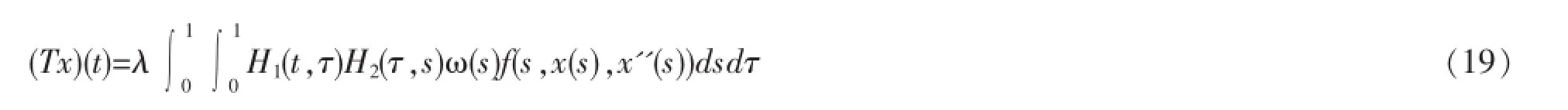


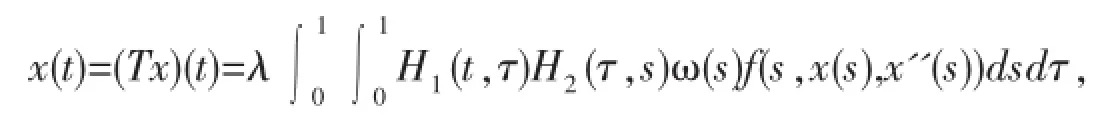
2 主要定理


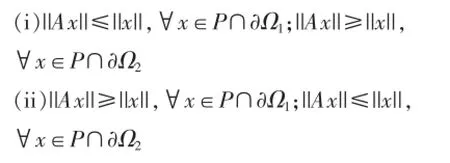




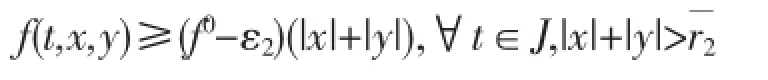






(Chongqing Real Estate College,Chongqing 401331,China)

