全微分法在隐函数求导中的应用研究*
尹 丽,高 辉
·基础理论研究·
全微分法在隐函数求导中的应用研究*
尹 丽,高 辉
(大连海洋大学理学院,辽宁大连 116023)
摘 要:将全微分法应用于隐函数求导中,对单个方程和方程组所确定的一元隐函数的一阶与二阶导数,单个方程和方程组所确定的二元隐函数的一阶与二阶偏导数进行了求解研究。结果表明:此方法使得隐函数求导变得通俗易懂,且不易出错,大大提高了解答此类问题的正确率,使隐函数求导不再成为学习高等数学的一个难点。
关键词:全微分法;复合函数;隐函数;求导;偏导数
1 引言
隐函数求导是高等数学的重要的知识点,也是初学者学习的难点。究其原因,传统的方法对隐函数求导:首先,应区分开自变量与函数;再次,需把握好自变量与函数间的关系,认识到:在求导过程中函数是关于自变量的中间变量;最后,实质是用复合函数求导法则的思路解决隐函数求导问题。而在实际练习中,自变量与函数间的关系是千变万化的。学生单一地依据求导法则去求解隐函数,复合函数的(偏)导数的时候,常会发现很难把握住函数变量间的关系,从而很容易造成问题的错解 。[1]
因此,本文将全微分法应用于隐函数求导中,对单个方程和方程组所确定的一元隐函数的一阶与二阶导数,单个方程和方程组所确定的二元隐函数的一阶与二阶偏导数进行了求解研究。
该方法的好处在于:利用全微分形式的不变性,不论自变量与函数如何变换,对自变量与函数始终“同等看待”,对他们“平等处理”,从而使问题简约,做题思路明了,解决方法标准,达到提高正确率的效果。
2 全微分法
全微分法实质上是应用函数全微分形式的不变性,在函数或隐函数的方程两边分别求全微分,最后求得函数的全微分,从而求得函数或隐函数的导数或偏导数。
全微分法以下面两定理为基础。
定理1(一元函数微分形式的不变性)设y= f(u),u=g(x)都可微,则函数y=f[g(x)]的微分为
即一个一元可微函数的微分总是等于该函数对某个变量的导数乘以该变量的微分。
定理2(二元函数全微分形式的不变性)设函数z=f(x,y)可微,不论x,y是自变量,还是中间变量,函数z的全微分形式总是
一般地,定理1和定理2可以推广到任意n元可微函数。
3 全微分法在隐函数求导中的应用
3.1 单个方程确定的一元隐函数的一阶与二阶导数


解 方程y=1+xey两边同时求微分:
自产自销,各推各的,分布零散,没有形成一个具体的体系,仅仅只是依靠自身是无法形成品牌和规模的。缺少品牌营销推广限制着民宿的经营,模仿其他民宿,零散的经营,没有经营理念和品牌营销的民宿注定跟不上现代旅游发展的步伐。
dy=d(1+xey)⇒dy=d1+dxey⇒dy=0+ eydx+xeydy⇒(1-xey)dy=eydx


3.2 方程组所确定的一元隐函数的一阶与二阶导数
例3[3]求由方程组所确定的函数的导数。
分析 本题方程组所确定的函数x=x(z),y =y(z)都是一元函数,适用定理1,把两个方程同时两边求微分,解出函数x的微分dx,解出函数y的微分dy,据定理1


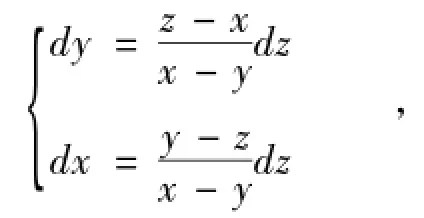


3.3 单个方程确定的二元隐函数的一阶与二阶偏导数


解对方程两边同时求微分d(x2+y2+z2-4z)=d0
2xdx+2ydy+2zdz-4dz=0
整理得(z-2)dz=-xdx-ydy
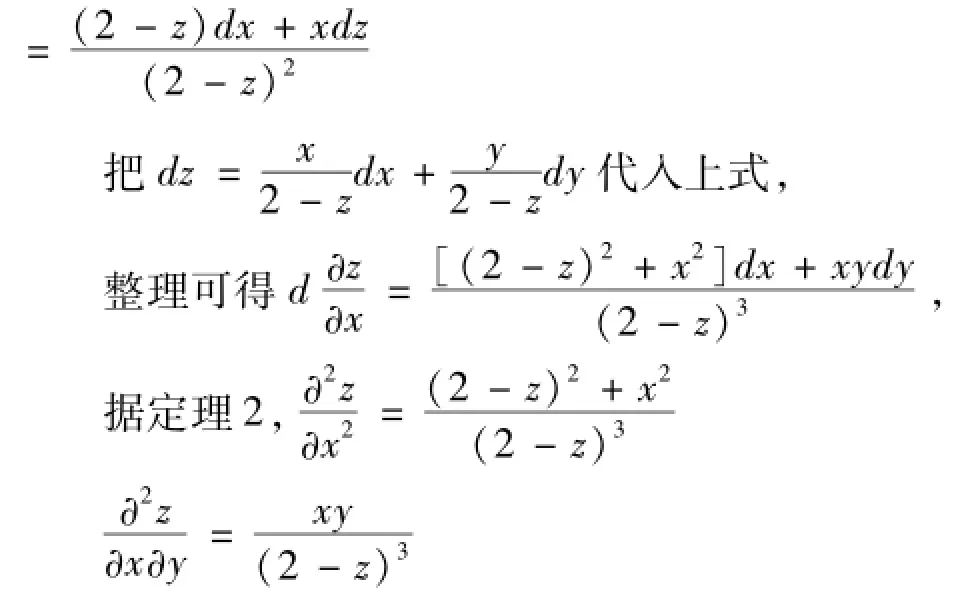
3.4 方程组所确定的二元隐函数的一阶与二阶偏导数
例7[3]求由方程组所确定的函数的偏导数
分析 本题方程组所确定的函数u=u(x,y),v=v(x,y)都是二元函数,适用定理2.
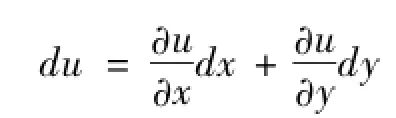
解 对方程组两边同时微分并整理

解方程
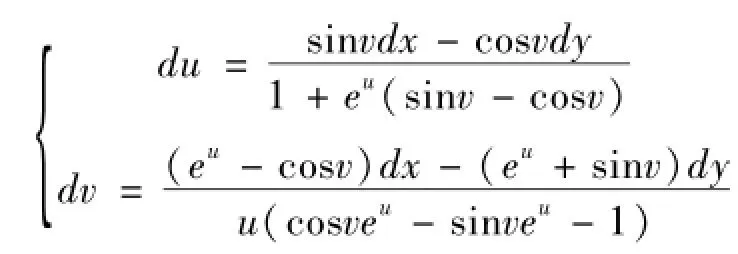

4 结论
微分形式不变性的妙处在于能够避开函数变量错综复杂的关系,抓住问题的本质,利用熟识的数学形式结构原型方便简洁地解决问题[4]。通过以上范例,把全微分法应用于隐函数求导中。发现利用全微分形式的不变性解决隐函数求导是一种简明、规范的数学方法。使用该方法,以不变应万变,使得隐函数求导变得通俗易懂,且不易出错,大大提高了解答此类问题的正确率,使隐函数求导不再成为学习高等数学的一个难点。
参考文献:
[1]蔡白光,郭纪云.全微分法在微分学中的应用[J].海南大学学报(自然科学版),2013(4):303-305.
[2]同济大学数学系.高等数学:上册[M].北京:高等教育出版社,2007.
[3]同济大学数学系.高等数学:下册[M].北京:高等教育出版社,2007.
[4]张艳琼.关于微分形式不变性的教学思考[J].高等数学研究,2013(3):44-46.
中图分类号:O172.1
文献标识码:A
文章编号:1673-6125(2016)02-0001-04
收稿日期:2016-03-11
作者简介:尹 丽(1981-),女,辽宁庄河人,大连海洋大学理学院讲师、硕士。主要研究方向:高等数学教学与研究。高 辉(1978-),女,辽宁庄河人,大连海洋大学理学院讲师、硕士。主要研究方向:高等数学教学与研究。
Application study of total differential method in solving derivation of implicit function
YIN Li,GAO Hui
(Dalian Ocean University,science Institute,Dalian,116023,China)
Abstract:The total differential method applied in implicit function derivation,for first and second derivative of one variable of implicit function determined by a single equation or the equations,first and second partial derivative of binary variable of implicit function determined by a single equation or the equations was studied to solve.The results show that this method makes the implicit function derivation become easy to understand.And when this method is used,it is not liable to make errors.This method can raise the exactness rate.Using this method makes implicit function derivation is no longer the difficulty of learning advanced mathematics.
Key words:Total differential method;Compound function;Implicit function derivation;Partial derivative

