Si和SiGe三极管Early效应模型及在电路仿真器中的应用综述
徐小波,张 林,王晓艳,谷文萍,胡辉勇,葛建华
(1.长安大学电子与控制工程学院,道路交通检测与装备工程技术研究中心,陕西西安 710064;2.西安电子科技大学综合业务网理论与关键技术国家重点实验室,陕西西安710071;3.西安电子科技大学微电子学院,宽禁带半导体材料与器件重点实验室,陕西西安 710071)
Si和SiGe三极管Early效应模型及在电路仿真器中的应用综述
徐小波1,2,张林1,王晓艳1,谷文萍1,胡辉勇3,葛建华2
(1.长安大学电子与控制工程学院,道路交通检测与装备工程技术研究中心,陕西西安 710064;2.西安电子科技大学综合业务网理论与关键技术国家重点实验室,陕西西安710071;3.西安电子科技大学微电子学院,宽禁带半导体材料与器件重点实验室,陕西西安 710071)
Early效应作为表征双极器件关键性能的因素之一,影响输出跨导、传输电流、基区渡越时间、电流增益、扩散电容等器件特性.本文从Early效应的基本定义出发,综述了Early电压的起源,模型的发展及其在Si和SiGe电路仿真器中的应用.具体为:(1)综述了Si三极管中的基本模型及在SPICE中处理过程,然后针对SPICE的缺陷,描述了VBIC模型中针对Early效应的改进.(2)由于SPICE和VBIC不能有效描述SiGe HBT中基区Ge组分引入.本文基于SiGe HBT标准化模型Mextram、HICUM对SiGe HBT的建模思想,综述了将其用于建立Early电压模型的方法.(3)总结了现有主流模型对Early效应的建模方法及优缺点.
Early效应;三极管;SPICE;积分电荷控制关系
1 引言
对于硅(Si)和硅锗(SiGe)三极管,输出跨导、传输电流、基区渡越时间、电流增益、扩散电容等等,这些表征器件核心性能的参数都与Early效应有关.发射结和集电结外加偏压引起对应空间电荷区宽度变化,导致准中性基区变宽或变窄,产生基区宽度调变效应.该效应由Early,J.M.于1952年开始研究[1],Early首次证明,在IC~VCE(集电极电流~集电极-发射极压降)特性曲线中,不存在零斜率dIC/dVCE,因此,由于基区宽度调制,输出电阻不会取无穷大.由于Early本人的工作,不管是零斜率还是它的物理基础(基区宽度调制)都被统称为Early效应.
对三极管的有效建模历史从Ebers Moll[2]模型开始,它仅仅包含两个背靠背二极管,并没有针对Early效应建模.基于Ebers Moll模型原理的Gummel Poon模型出现于1970年,开始涵盖Early效应[3],并在后续给出了改进[4],这就是后面电路仿真器SPICE中的内嵌模型基础.Gummel发现,将所有IC~VCE特性曲线反向延长,近似相交于一点,该点对应电压值被称为Early电压.模型中通过引入归一化基区电荷qb来包括Early效应.Lindholm[5]于1971年、Logan[6]于1972年给出了基于测试结果Early效应经验公式,Clark[7]从理论角度建立了物理模型,并给出了公式适用范围.以上所有分析都基于一个前提:基区宽度足够大.1975年,Rohr[8]从理论上定性分析了窄基区三极管情况,如果基区足够窄,载流子不发生碰撞,IC~VCE曲线斜率可以为零,Early效应消失.不过直到今天,由于工艺因素和击穿电压限制,基区中载流子仍然会发生碰撞.1983年,Hart[9]针对集电结电压变化引起对应耗尽层电容变化,导致Early电压不再为常数的情况,引入平均值作为等效Early电压.在当时工艺条件下,这是合理的.典型情况下的Early效应随集电结电压变化不大,每伏外加偏压引起的Early电压变化小于10%.1987年Herbert和Roulston[10]提出了可变基区电荷模型,建立了具体的耗尽层电荷变化解析模型.1991年Kuntman[11]建立了Early电压基于内建电势和电容梯度系数的物理模型,并且引入了与三极管工作点无关的参数,在与SPICE兼容的同时,只需要额外一组数据,就可以获得更高的模型精度.几年后,McAndrew[12,13]综合考虑了发射结和集电结耗尽层电荷整体同时对Early效应的影响,而不是假设发射结电荷变化决定反向Early电压,集电结电荷变化决定正向Early电压,使模型精度进一步提高.基于SPICE在描述三极管上的局限性,1996各大主流电路设计和制造公司研究人员联合推出了基于SPICE的改进模型VBIC(Vertical Bipolar Intercompany Model)[14],建立了Early电压与电容平滑因子、内建电势、梯度系数、结偏压的关系模型,并优化了耗尽层电容与扩散电容之间的转换.
尽管异质结的概念早在1951由Shockly提出并定义为由两种不同半导体形成的pn结[15],异质结晶体管(HBT)的概念也早在1957就被Kroemer提出来,并给出一般性设计原则[16,17],但是受限于薄膜生长技术,直到1987才制造出第一个有用的SiGe HBT[18],1990年研制出性能超过Si三极管(BJT)的SiGe HBT[19,20],1994年第一代SiGe HBT技术进入商用[21],1995年出现与互补金属氧化物半导体(CMOS)兼容的SiGe HBT,并产生了第一代SiGe HBT双极CMOS (BiCMOS)工艺[22].从那以后,SiGe HBT BiCMOS技术迅速发展.
由于SiGe HBT速度更快,性能更好,并且与现有Si BJT工艺兼容,现有主流双极或BiCMOS电路多数都在基区引入锗(Ge)组分,从而采用SiGe HBT制造高速芯片.而SPICE和VBIC都不能有效考虑Ge组分对电路电学参数影响,这其中就包括Early效应.为有效描述SiGe HBT的Early效应,2003年Mijalkovic[23]通过假设准中性基区边缘权重空穴浓度存在分段指数分布,引入参数(分段考虑,模型相对复杂.2011年Xu[24]提出在Early效应建模过程中去除耗尽层电荷概念,改用古麦耳数(Gummel number)来代替,得到了简单精确的解析模型.主流标准化SiGe HBT电路仿真模型Mextram (Most Exquisite Transistor Model)[25]通过传统Si器件Early电压模型,反向求出近似耗尽层宽度,然后考虑Ge组分因素,将模型扩展到SiGe HBT[26].
随着芯片尺寸逐年减小,在现代高速电路中,三极管基区宽度越来越窄,导致准中性基区宽度变化对整个基区总电荷影响越来越大,从而对整个三极管的电流、电容、充放电的干扰逐年增大,因此对Early效应的研究很有必要.本文拟通过从Early电压的基本定义开始,综述Early效应在Si BJT和SiGe HBT的建模差别,以及在相关商用化电路仿真器中的应用,主要为SPICE、VBIC、Mextram和HICUM (HIgh CUrrent Model)[27].最后总结了现有主流模型对Early效应的建模方法及优缺点,为现代双极或BiCMOS电路设计提供理论基础.
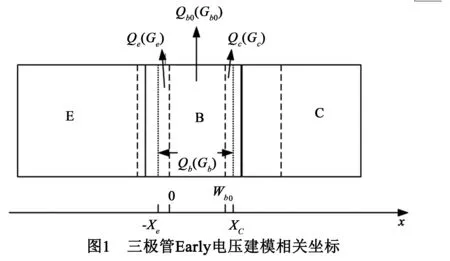
本文所建模型相关坐标参数如图1所示,虚线为平衡态时耗尽区边界,点线表征外加偏压引起对应边界移动.x轴0点设在零偏时发射结耗尽区基区边缘处,Wb0为零偏时准中性基区宽度,Xe和Xc分别为任意偏置下发射结和集电结耗尽区在基区边缘的位置.Qb(Gb)和Qb0(Gb0)分别为任意偏压和零偏压下基区电荷(古麦耳数).Qe(Ge)和Qc(Gc)分别为发射结和集电结耗尽层电荷(古麦耳数).其中古麦耳数的定义在第三部分.
2 Si三极管与SPICE模型
对Si BJT的有效建模要求输出跨导g0模型精确.在小偏置下,g0由基区宽度随偏压的变化控制,它是由发射结和集电结边缘的位置改变决定,即Early效应.
双极器件的集约模型(compact model),如Gummel Poon(GP)模型,采用解析表达式描述基区宽度调制效应[3].作为电路仿真工具如SPICE中内嵌GP模型,要求提供模型参数作为输入.大多数模型参数都有具体物理意义,用来描述特定器件特性.与Early效应相关的就是正向与反向Early电压.需要明确的是,这些参数物理意义明确,能够与更基础的工艺参数如基区、集电区掺杂浓度密切关联起来.作为最成熟的半导体材料器件,针对Si BJT的Early效应建模多数都在二三十年前[28-31],首先来回顾Early电压的由来和基本定义,这有助于后面SiGe HBT中Early效应的分析.SPICE模型用常数跨导g0来近似Early效应.尽管这个近似使Early电压容易提取,但是以降低g0建模精度为代价.
在GP模型中,Early电压被转换为归一化基区电荷qb随外加发射结和集电结偏压引起的变化.GP BJT模型基础为1970年的传输电流积分电荷控制ICCR (Integral Charge Control Relation)模型[3],该表达式的雏形由Moll和Rose[32]于1956年提出,Ghosh[33]于1967年改进并提出一个更完整的电流模型,可惜为数值结果,不能用于集约模型.三年后Gummel和Poon给出了下面的解析公式[3]
(1)
其中Ic为集电极电流,Is为三极管饱和电流,Vbe和Vbc分别特指本征发射结和集电结电压,VT=kT/q为热电势,k为玻尔兹曼常数,T为绝对温度,q为电子电荷量.qb描述基区宽度调制和大注入对输出电流的影响,qb表达式为
(2)
q1和q2分别为基区宽度调制和大注入相关参数,不考虑大注入情况下,q2= 0,qb= q1,传输电流公式(1)的分母仅剩下q1描述基区宽度调制.q1定义式为[3]
(3)
(4)
其中NB为x点处掺杂浓度.公式第一项和第三项分别为发射结和集电结耗尽层电荷Qe和Qc,分别与反向和正向Early效应关联,第二项为Qb0.Qe和Qc分别可以用对应结耗尽层电容表示,引入归一化发射结和集电结耗尽层电荷qe和qc
(5)
其中Cje(c)为发射结(集电结)耗尽层电容.在反向和正向小偏压下,耗尽层电容近似为常数,可以取为零偏时的平均值Cje(c)0,Qe≈ VbeCje0,Qc≈ VbcCjc0,因此
(6)
其中Vaf和Var分别为正向和反向Early电压,定义为[3]
(7)
这就是Gummel和Poon对Early电压的原始定义,即Cje0Var=Cjc0Vaf=Qb0.因此小偏置下,可以近似为
qb=q1=1+qe+qc
(8)
(9)
如果采用上面的模型,集电极电流可以写为
(10)
其中Ic0为不考虑Early效应的集电极电流.
在原始SPICE模型中,Early电压被当作常数.以Var为例,根据等式,显然必须假设Cje为常数.当发射结反偏,Cje几乎不变,反向Early电压为常数的假设适用,但是发射结正偏,将导致很大的误差.同理,对于Vaf,当集电结反偏(器件正向工作模式),Cjc为常数的假设适用,但是如果集电结正偏(反向或者饱和模式),对于qc的描述需要更精确的模型,取决于qc在qb表达式中的重要性.
值得说明的是,尽管常数Early电压假设可能会产生很大的误差,这个误差在很多时候可以接受.这是由于qc(qe)在整个归一化基区电荷qb中通常不是主要组成部分,不起决定作用.即Qe(Qc)一般比Qb0小很多,因此qe(qc)一般远远小于1.
进一步,如果Early电压足够大,即|Vbe|< (11) 等式(11)就是实际应用中的SPICE Gummel Poon (SGP)模型.即此时的Var和Vaf为SPICE模型中所用的值. 对上式所作的近似,可以避免数值问题,如q1改变符号的时候,出现被除数为零的情况.这在仿真器迭代过程中可能发生,只要反向Early电压绝对值足够小,而这在现代BJT中很常见.另外一方面,可以产生常数Early电压,这在工业应用上很方便.简单解释如下:利用等式的近似,集电极电流可以写为 (12) 在正向工作模式下,g0可以为表示为 (13) 其中Isat=Isexp(qVbe/kT).等式的几何解释表明Vaf可以从I~V曲线的反向延长线与Vce的交点得到.如图2所示. 在随后20多年发展中,SPICE的使用者发现,随着三极管尺寸减小,很多以前忽略的寄生效应变得越来越重要.比如随着集成度提高,器件自热效应对性能影响越来越大,而SPICE并没有描述自热;再比如,SPICE中包含发射区、基区和集电区,为三端口模型,而在现代电路中,衬底寄生电流、电压不能忽略.因此,为了改进SPICE模型,AT&T、Texas Instruments、Analog Devices、Hewlett-Packard、Motorolar、Analogy、MetaSoftware、National Semiconductor、IBM、Intel/Philips等公司合作于1996年推出了第一版VBIC95模型[14,34],由于是作为SPICE的替代模型,VBIC的主体模型与SPICE非常类似,为SPICE的直接扩展,尽可能在原有模型中引入一些额外的公式或者系数来进行弥补.这中间就包括针对Early电压模型的修正.VBIC模型在后续几年得到进一步完善[35,36]. 在上述SPICE模型建立过程中,可以看到,Early电压的结果包含一个前提:采用零偏压耗尽层电容Cj0来代替耗尽层电容Cj,因此为常数.由于现代BJT中普遍采用窄基区技术实现高速和高增益,qc(qe)在整个归一化基区电荷qb中作用大大增加,即使有效基区宽度发生很小的变化,器件性能也有很大的改变.因此对SPICE中常数Early电压模型修正的必要性大增. 在现代应用于Si BJT的VBIC模型中,Early效应最重大的改变在于用Cj替代Cj0,获得耗尽层电容模型后,通过CjeVar=VjcVaf=Qb0给出Early电压模型.同时,为了更符合实际,耗尽层电容也进一步优化如下: 在反向和正向小偏压下,归一化耗尽层电容cj为[36] (14) 其中V为外加偏压,φ、m分别为对应结内建电势和梯度系数,FC为结电压与内建电势的比值,反映两者之间的接近程度,A为耗尽层电容平滑参数.如果发射结和集电结耗尽层电容平滑参数AJE<0,AJC<0,cj将平滑出现最大值,否则cj将线性增加,与SPICE吻合. 图3给出了耗尽层电容在SPICE和VBIC的中的差别[37].VBIC中,外加结偏压超过内建电势后,电容固定为常数,不再变化,更好的描述了耗尽层电容和扩散电容之间的转换. 显然,VBIC模型通过用偏置密切相关的耗尽层电容模型取代了零偏时的固定耗尽层电容值,使Early电压结果不再为常数,而是同样受偏置电压影响.该模型结果与实际器件测试结果符合更好[38]. 由于VBIC模型在SGP模型的基础上作了诸多改进,仿真精度大为提高.实际上,VBIC兼容SGP模型,参数如果取缺省值就简化为SGP模型,因此VBIC取代SPICE成为BJT模型的一种新工业标准.但如果将模型直接用于HBT器件并不是非常合适.尽管也有将VBIC应用于SiGe HBT的情况[39~42],但是模型仍然存在问题有待解决.比如:VBIC模型中没有考虑HBT中热电阻与温度的不同关系[43];发射结和集电结电流项中的理想因子与温度的关系等等.当然也包括没有考虑到Early效应在SiGe HBT中的变化,电流对异质结中耗尽层电容的调节作用没有相关体现. 下面将仔细分析SiGe HBT中的Early电压模型. 现有的大多数仿真器基于SGP模型或者其改进型,对于SiGe HBT,基区中Ge的加入导致SGP模型不能充分描述Early效应[44].SPICE模型将Early电压当作常数,后续改进版本VBIC模型克服了这个限制,但是没有考虑基区Ge引入对Early效应的影响[14],针对SiGe HBT的Early效应描述相对粗糙. 在Si的SGP模型中,集电极电流通过积分电荷控制关系ICCR描述,引入假设一定偏压下基区电荷与基区古麦耳数成正比.对于SiGe晶体管,如果Ge组分在基区存在分布梯度,基区带隙不再一致,因此导致基区电荷不再与古麦耳数成比例.忽略扩散电容和大注入效应,集电极电流可以表示为[43] (15) (16) Gb0为上式第二项,第一项和第三项分别为Ge和Gc,因此Gb=Ge+Gb0+Gc.Dn是SiGe基区少子扩散系数,ni0为Si本征载流子浓度,ni(x)是依赖于Ge组分的本征浓度. 类比Si BJT中Early电压的建模思想,Gb/Gb0可以重写为[23,45] (17) (18) 应该看到,如果ni(x),Dn(x)为常数,古麦耳数G与对应电荷Q成正比,式(18)简化为VBIC模型,进一步,如果耗尽层电容为常数,式(18)简化为SPICE模型. 与基区Ge加入引起能带变化相比,扩散系数的影响很小,因此可以认为是常数.而能带的变化带来本征载流子浓度指数变化,ni(x)和ni0不相等. 以基区Ge组分线性增长为例,如图4所示,虚线代表耗尽层,点线表示基区Ge分布. 假设基区掺杂浓度为常数,Ge组分在基区线性分布,基区本征载流子浓度可以写为[45] (19) 其中A为常数,η=△Eg/kT,△Eg为Ge组分引入的能带差,通过ni(x)表达式求出Ge和Gc,进而代入式(18)得到最终模型[45] (20) 观察上式可知,与VBIC模型Qb0/Cj相比,式引入了与基区能带变化相关的参数项,从而实现精确描述SiGe HBT. 作为针对SiGe HBT的主流标准化仿真器模型,1985年Philip研究院发布了第一个版本Mextram[27].不同于SPICE基于电荷控制原理,Mextram直接基于中性基区的少数载流子的微分方程的解,获得电流、电荷与发射结、集电结注入的少数载流子浓度的关系,电流与电荷彼此独立.而浓度又与对应结偏压关联.最新版本为Mextram level 504,可在NXP公司的官网上找到最新信息[25].Mextram获得了广泛使用,比如NXP公司的Pstar,Cadence公司的Spectre,Agilent公司的ADS等等业界最主流的双极电路仿真器都内嵌了Mextram模型.当然Mextram也能够很好的仿真Si三极管. 由文献报道的SPICE与Mextram模型对应输出特性测试结果可知[46,47],显然,两者差别很大.这其中就包括Early效应的差别. Mextram较好地解决Ge组分对Early效应的影响,主要思想为通过传统Si器件Early电压模型,反向求出近似耗尽层宽度,采用古麦耳数代替耗尽层电荷,然后将其扩展到SiGe HBT,得到的核心公式为[26]: (21) 其中Vdel,be(c)=Qe(c)/Cje(c).可以证明,式(21)与式(20)模型结果一致.因此这两个公式即为Mextram中的Early电压模型. 针对异质结中基区能带变化引起的Early电压改变,Mijalkovic[23]通过假设准中性基区边上权重空穴浓度存在分段指数分布,引入参数α,对SiGe HBT的Early效应进行精确描述,但是模型建立相对复杂,而且不能直接求解参数α,在仿真器中将引起收敛问题,因此没有被电路仿真模型采用. 至于工业应用中的另一个标准化双极模型HICUM[48,49],同样适用于SiGe HBT[50].从名字可知,开发的重点为高速大电流场景应用[51~53].自从第一版本发布开始[54-56],到现在最近的一次更新为2013年12月,版本为HICUM Lver2 version 2.33[25].由于高速电路的设计和优化要求对晶体管动态特性精确建模,表征动态特性的耗尽层电容、渡越时间、电荷量等参数被认为是模型的基本变量,并采用静态与动态耦合的方式描述,因此整个模型中即使去掉一些人为引入的参数,也能够精确描述器件.实际上,HICUM模型取消了Early电压的概念.由此可知,建立HICUM模型的理论基础与Mextram完全不一样. 虽然Early电压在HICUM中意义不大,参数提取过程中并不需要测量获得Early电压.但为了保持前后文连续,我们基于HICUM模型的基本原理,即扩展积分电荷控制关系GICCR (Generalized ICCR)[57~59],给出Early效应的分析,为针对其它模型中的Early电压优化提供理论支撑. 基于GICCR,将HICUM模型中传输电流改写为对应的传统形式: (22) 其中Qp,T为整个三极管的电荷,Qp0为平衡时的空穴电荷. Qp,T=Qp0+heQe+hcQc+Qf,T+Qr,T (23) he和hc为对应的权重因子,Qf,T和Qr,T分别为整个三极管存储的正向和反向少子电荷,包括中性发射区、基区、集电区少子电荷量. 从HICUM模型中传输电流描述可以看出,模型中包含了整个三极管区域的所有电荷,而前面的模型分析范围都局限在基区.这也是GICCR名字的由来:将传统积分电荷控制关系从基区扩展到整个三极管. 从Early效应的角度,效应的发生依赖于发射结和集电结耗尽层宽度的变化,因此与对应分量heQe和hcQc相关.从前文Mextram模型分析可以看出,一般情况下,由于基区禁带宽度不均匀,Mextram中用Gb(e)来取代相应电荷Qb(e),但是在HICUM中再次出现了耗尽层电荷的概念,而将禁带变化的影响用权重因子来表示.一般情况下,基区任意一点的禁带宽度都与其它点不一定一致,因此理论分析的时候可以用平均权重因子来表示,达到简化模型的目的,而在工业化标准模型中,必须采用与实际测量参数相结合的方式,通过数据拟合,给出权重因子符合实际的数学表达式,该表达式为半经验公式.实际上整个HICUM就是一个半经验模型[60],在权重因子部分的处理正是这么做的.假设基区禁带宽度线性改变,相关表达式为[61,62]: (24) (25) (26) 其中,he0为零偏时权重因子,aG和ahe包含Ge组分引入引起的禁带宽度变化,vj、Vde和ze为描述集电结耗尽层电容与偏置关系的参数,同样为半经验公式,相当复杂. 其中基于上面的结果,正反向Early电压可以计算为: (27) 从HICUM的建模过程可知,模型公式中某些参数的确定依赖于工艺,通过数据拟合,获得半经验结果.因此与实际测试的结果吻合更好.缺点在于模型稍显复杂. Early效应由发射结和集电结耗尽层电荷在外加偏压下的变化引起,导致基区宽度发生变化.在双极器件的电路设计中,针对Early效应的精确建模很有必要.Early电压作为表征电流稳定性的参数,直接或间接与器件中诸多关键参数关联,包括输出跨导、传输电流、基区渡越时间、电流增益、扩散电容等器件电学特性.20到30年前年的主流三极管基区宽度相对比较大,有效基区宽度改变量与中性基区相比还比较小,Early效应的粗略建模对器件性能影响不大;但是在现代双极电路中,随着工艺尺寸缩小,基区宽度减薄至几十纳米,基区宽度的微小变化将极大改变器件参数,因此需要精确建模. 本文研究三极管的Early效应,从Early效应基本定义出发,综述了Early电压起源,模型发展及其在Si和SiGe电路仿真器中的应用. 作为应用最广泛的电路仿真模型,SPICE将Si BJT的Early电压当作常数对待,在建模过程中认为发射结和集电结耗尽层电容不变,取值为零偏时耗尽层电容.随着Si BJT尺寸减小,为了克服SPICE的局限性,VBIC模型将耗尽层电容当作变量,依赖于外加偏压,在此基础上建立了随外加电压发生变化的Early电压模型,VBIC比SPICE与测试数据的一致性大幅提高.随着SiGe HBT在现代双极和BiCMOS电路中的大量使用,为了描述基区Ge组分对Early效应的影响,Mextram将输出电流方程中发射结和集电结耗尽层电荷替换为古麦耳数,古麦耳数定义中不仅包含基区空穴浓度,还描述了Ge组分及分布导致基区禁带宽度变窄,从而引起本征载流子浓度变化.因此很好的解决了基区Ge引入带来的Early电压模型改变.由于另一个适用于SiGe HBT的标准化模型HICUM去除了Early电压,本文基于HICUM对SiGe HBT的建模思想GICCR,描述了将其用于建立Early电压模型的方法.在HICUM电流方程中,依然包含耗尽层电荷,而将Ge组分的影响采用权重因子的方式来实现.由于Ge引入导致基区禁带宽度不一致,权重因子的确定一方面依赖于基本物理原理,另一方面依赖于工艺拟合.因此模型精度高,但是建模复杂. 因此,本文综述了Si三极管中的基本模型及在SPICE中处理过程,然后针对SPICE的缺陷,描述了VBIC模型中针对Early效应的改进;综述了Mextram、HICUM两大标准化模型针对基区Ge组分引入进行的处理方法,并将其思想用于建立Early电压模型.本文综述为Si BJT和SiGe HBT高速电路设计和仿真提供了重要参考. [1]Early J M.Effects of space-charge layer widening in junction transistors[J].Proceedings of the IRE,1952,40 (11):1401-1406. [2]Ebers J J,Moll J L.Large-signal behavior of junction transistors[J].Proceedings of the IRE,1954,42 (12):1761-1772. [3]Gummel H K,Poon H C.An integral charge control model of bipolar transistors[J].The Bell System Technical Journal,1970,49 (5):827-852. [4]Poon H C.Modeling of bipolar transistor using integral charge-control model with application to third-order distortion studies[J].IEEE Transactions on Electron Devices,1972,19 (6):719-731. [5]Lindholm F A,Hamilton D J.Incorporation of the early effect in the ebers-moll model[J].Proceedings of the IEEE,1971,59 (9):1377-1378. [6]Logan J,Lindholm F A,Rohr P,Hamilton D J.Modeling the "Early Effect" in bipolar transistors using an empirical but effective parameter[J].Proceedings of the IEEE,1972,60 (3):335-336. [7]Clark L E.Physical dependencies and modeling of output admittances and gain-voltage relationships in bipolar transistors[J].Proceedings of the IEEE,1972,60 (11):1445-1446. [8]Rohr P,Lindholm F A.Modifications of equivalent circuits for narrow-base transistors[J].IEEE Journal of Solid-State Circuits,1975,10 (1):65-72. [9]Hart B L.Modeling the early effect in bipolar transistors[J].IEEE Journal of Solid-State Circuits,1983,18 (1):139-140. [10]Hebert F,Roulston D J.modeling of narrow-base bipolar transistors including variable-base-charge and avalanche effects[J].IEEE Transactions on Electron Devices,1987,34 (11):2323-2328. [11]Kuntman H.Novel Modification on SPICE BJT model to obtain extended accuracy[J].IEE Proceedings,Part G:Circuits,Devices and Systems,1991,138 (6):673-678. [12]McAndrew C C,Nagel L W.Early Effect modeling in SPICE[J].IEEE Journal of Solid-State Circuits,1996,31 (1):136-138. [13]McAndrew C C,Nagel L W.SPICE early modeling bipolar transistors[A].IEEE Bipolar/BiCMOS Circuits and Technology Meeting[C].Minneapolis:IEEE,1994.144-147. [14]McAndrew C C,Seitchik J A,Bowers D F,et al.VBIC95,the vertical bipolar inter-company model[J].IEEE Journal of Solid-State Circuits,1996,31 (10):1476-1483. [15]William S.Circuit element utilizing semiconductive material[P].US Patents,1951:2569347,1951-09-25. [16]Kroemer H.Theory of a wide-gap emitter for transistors[J].Proceedings of the IRE,1957,45 (11):1535-1537. [17]Kroemer H.Quasi-electric and quasi-magnetic fields in nonuniform semiconductors[J].RCA Review,1957,18 (3):332-342. [18]Iyer S S,Patton G L,Delage S S,et al.Silicon-Germanium base heterojunction bipolar transistors by molecular beam epitaxy[J].IEEE Electron Device Letters,1988,9(4):165-167. [19]Patton G L,Comfort J H,Meyerson B S,et al.63-75 GHz fTSiGe-base heterojunction bipolar technology[A].IEEE symposium on VLSI Technology[C].Honolulu:IEEE,1990.49-50. [20]Patton G L,Comfort J H,Meyerson B S,et al.75-Ghz fTSiGe-base heterojunction bipolar transistors[J].IEEE Electron Device Letters,1990,11 (4):171-173. [21]Harame D L,Schonenberg K,Gilbert M,et al.A 200 mm SiGe-HBT technology for wireless and mixed-signal applications[A].IEEE International Electron Devices Meeting[C].San Francisco:IEEE,1994.437-440. [22]Nguyen-Ngoc D,Harame D L,Malinowski J C,et al.A 200 mm SiGe-HBT BiCMOS technology for mixed signal applications[A].IEEE Bipolar/BiCMOS Circuits and Technology Meeting[C].Minneapolis:IEEE,1995,89-92. [23]Mijalkovic S.Generalised early factor for compact modelling of bipolar transistors with non-uniform base[J].Electronics Letters,2003,39 (24):1757-1758. [24]Xu X-B,Zhang H-M,Hu H-Y,et al.Early effect modeling of silicon-on-insulator SiGe heterojunction bipolar transistors[J].Chinese Physics B,2011,20(5):058502-1-6. [25]van der Toorn R,Paasschens J C J,Kloosterman W J,The mextram bipolar transistor Model[EB/OL].http://www.nxp.com/wcm-documents/models/bipolar-models/mextram/mextramdefinition.pdf,2016-03-22 [26]Paasschens J C J,Kloosterman W J,Havens R J.Modelling two SiGe HBT specific features for circuit simulation[A].IEEE Bipolar/BiCMOS Circuits and Technology Meeting[C].Minneapolis:IEEE,2001,38-41. [27]De Graaff H C,Kloosterman W J.New formulation of the current and charge relations in bipolar transistor modeling for CACD purposes[J].IEEE Transactions on Electron Devices,1985,32 (11):2415-2419. [28]Pyne D,Khokle W S.Analysis of the Early voltage in bipolar transistors[J].IEEE Transactions on Electron Devices,1986,33 (10):1539-1544. [29]Scott D,Roulston D.IC-VCE Characteristics of double diffused bipolar transistors under low level injection[J].Solid-State Electronics,1980,23 (3):201-207. [30]Van Der Ziel A.A sufficient condition for an early voltage[J].Solid-State Electronics,1974,17 (1):108-110. [31]Yuan J S,Liou J J.An improved early voltage model for advanced bipolar transistors[J].IEEE Transactions on Electron Devices,1991,38 (1):179-182. [32]Moll J L,Ross I M.The dependence of transistor parameters on the distribution of base layer resistivity[J].Proceedings of the IRE,1956,44 (1):72-78. [33]Ghosh H N,De La Moneda F H,Dono N R.Computer-aided transistor design,characterization,and optimization[J].Proceedings of the IEEE,1967,55 (11):1897-1912. [34]Najm F.VBIC95:An improved bipolar transistor model[J].IEEE Circuits and Devices Magazine,1996,12 (2):11-15. [35]McAndrew C.Using the VBIC Bipolar Transistor Model[EB/OL].http://www.ece.uci.edu/docs/hspice/hspice-2001-2-110.html,2016-03-22. [36]McAndrew C.VBIC fundamentals[EB/OL].http://www.designers-guide.org/VBIC/references.html,2016-03-22. [37]McAndrew C,Seitchik J,Bowers D,Dunn M,et al.VBIC95:An improved vertical,IC bipolar transistor model[A].IEEE Bipolar/BiCMOS Circuits and Technology Meeting[C].Minneapolis:IEEE,1995,170-177. [38]Xiaochong C,McMacken J,Stiles K,et al.Comparison of the New VBIC and conventional Gummel-Poon bipolar transistor models[J].IEEE Transactions on Electron Devices,2000,47 (2):427-433. [39]Senapati B,Maiti C K.Advanced SPICE modelling of SiGe HBTs using VBIC model[J].IEE Proceedings- Circuits,Devices and Systems,2002,149(2):129-135. [40]Kyungho L,Dae-Hyung C,Kang-Wook P,et al.Improved VBIC model for SiGe HBTs with an unified model of heterojunction barrier effects[J].IEEE Transactions on Electron Devices,2006,53 (4):743-752. [41]Woods B O,Mantooth H A,Cressler J D.SiGe HBT compact modeling for extreme temperatures[A].Semiconductor Device Research Symposium[C].College Park:IEEE,2007.1-2. [42]DiVergilio A,Zampardi P,Newton K.VBIC:A new standard in advanced bipolar modeling[J].IBM MicroNews,1999,5(4):Q4. [43]张万荣,李志国,王立新,等.Si/ SiGe/ Si 双异质结晶体管(HBT) 的负阻特性[J].电子学报,2001,29(8):1132-1134. Zhang W R,Li Z G,Wang L X,et al.Negative resistance characteristics of Si/SiGe/Si double heterojunction bipolar transistors[J].Acta Electronica Sinica,2001,29(8):1132-1134.(in Chinese) [44]Kroemer H.Two integral relations pertaining to the electron transport through a bipolar transistor with a nonuniform energy gap in the base region[J].Solid-State Electronics,1985,28(11):1101-1103. [45]Xu X-B,Zhang H-M,Hu H-Y,et al.Early effect of SiGe heterojunction bipolar transistors[J].Solid-State Electronics,2012,72:1-3. [46]Paasschens J C J,Kloosterman W J,Havens R J,de Graaff H C.Improved modeling of output conductance and cut-off frequency of bipolar transistors[A].IEEE Bipolar/BiCMOS Circuits and Technology Meeting[C].Minneapolis:IEEE,2000.62-65. [47]Paasschens J C J,Kloosterman W J,Havens R J,et al.Improved compact modeling of output conductance and cutoff frequency of bipolar transistors[J].IEEE Journal of Solid-State Circuits,2001,36(9):1390-1398. [48]Schroter M,Krause J,Rinaldi N,et al.Physical and electrical performance limits of high-speed SiGeC HBT-Part II:lateral scaling[J].IEEE Transactions on Electron Devices,2011,58(11):3697-3706. [49]Schroter M,Wedel G,Heinemann B,et al.Physical and electrical performance limits of high-speed SiGeC HBTs-Part I:vertical scaling[J].IEEE Transactions on Electron Devices,2011,58(11):3687-3696. [50]Schroter M,Chakravorty A,Compact Hierarchical Modeling of Bipolar Transistors with HICUM [M].Singaproe:World Scientific,2010. [51]Schroter M.High-frequency circuit design oriented compact bipolar transistor modeling with HICUM[J].IEICE Transactions on Electronics,2005,88(6):1098-1113. [52]Schroter M,Walkey D J.Physical modeling of lateral scaling in bipolar transistors[J].IEEE Journal of Solid-State Circuits,1996,31(10):1484-1492. [53]Schroter M,Walkey D J.Correction to "Physical modeling of lateral scaling in bipolar transistors"[J].IEEE Journal of Solid-State Circuits,1998,33(1):171-171. [54]Schroter M.Simulation and modeling of the low-frequency base resistance of bipolar transistors and its dependence on current and geometry[J].IEEE Transactions on Electron Devices,1991,38(3):538-544. [55]Rein H M,Schroter M.A compact physical large-signal model for high-speed bipolar transistors at high current densities-Part II:Two-dimensional model and experimental results[J].IEEE Transactions on Electron Devices,1987,34(8):1752-1761. [56]Schroter M,Rein H M.Transit time of high-speed bipolar transistors in dependence on operating point,technological parameters,and temperature[A].IEEE Bipolar Circuits and Technology Meeting[C].Minneapolis:IEEE,1989.250-253. [57]Schroeter M,Rein H M.Two-dimensional modeling of high-speed bipolar transistors at high current densities using the integral charge-control relation[J].Physica B:Physics of Condensed Matter &C:Atomic,Molecular and Plasma Physics,Optics,1984,129(1-3):332-336. [58]Rein H M,Stubing H,Schroter M.Verification of the integral charge-control relation for high-speed bipolar transistors at high current densities[J].IEEE Transactions on Electron Devices,1985,32(6):1070-1076. [59]Schroter M,Friedrich M,Rein H M.A generalized integral charge-control relation and its application to compact models for silicon-based HBT′s[J].IEEE Transactions on Electron Devices,1993,40(11):2036-2046. [60]Schroter M,Rein H M,Rabe W,et al.physics- and process-based bipolar transistor modeling for integrated circuit design[J].IEEE Journal of Solid-State Circuits,1999,34(8):1136-1149. [61]Rein H,Schroter M.Base Spreading resistance of square-emitter transistors and its dependence on current crowding[J].IEEE Transactions on Electron Devices,1989,36 (4):770-773. [62]Schroter M,Pawlak A,Mukherjee A.A geometry scalable physics-based compact bipolar transistor model[EB/OL].https://www.iee.et.tu-dresden.de/iee/eb/forsch/Hicum-PD/Hicum23/hicum-L2V2p34-manual.pdf,2016-03-22 徐小波男,1983年生于安徽安庆.长安大学教师.研究方向为高速SiGe器件及电路设计,薄膜电池设计. E-mail:xuxiaobo@chd.edu.cn 张林男,1981年生于安徽马鞍山.长安大学教师,研究方向为功率器件及电路设计. Review on Early Effect Model of Si and SiGe Transistors and Applications to Circuit Simulators XU Xiao-bo1,2,ZHANG Lin1,WANG Xiao-yan1,GU Wen-ping1,HU Hui-yong3,GE Jian-hua2 (1.Road Traffic Detection and Equipment Engineering Research Center,School of Electronic and Control Engineering,Chang′an University,Xi′an,Shaanxi 710064,China; 2.National Key Lab.on ISN,Xidian University Xi′an,Shaanxi 710071,China; 3.Key Laboratory for Wide Band-Gap Semiconductor Materials and Devices,School of Microelectronics,Xidian University,Xi′an,Shaanxi 710071,China) As a key factor representing the bipolar transistor characteristics,the Early effect influences the output transconductance,the transfer current,the base transit time,the current gain,the diffusion capacitance,and so on.In this paper,we begin with the primary definition of the Early effect,overview the origin of the Early voltage,the development of the model,and the applications to Si and SiGe circuit simulators,with details as follows:(1) Summarize the basic Early effect model of the Si bipolar transistor,and the introduction into SPICE,then describe the improvement of VBIC model in view of limitations of SPICE.(2) As SPICE and VBIC are unable to describe the introduction of Ge profile into the base,we review the modeling methods of the Early voltage with SiGe HBTs,based on the modeling ideas of Mextram and HICUM,two SiGe HBT standard models.(3)Sum up the strengths and weaknesses of present models for the Early effect. Early effect;bipolar transistor;SPICE;integral charge control relation(ICCR) 2015-01-14; 2016-03-20;责任编辑:蓝红杰 中国博士后科学基金(No.2013M540732);国家自然科学基金(No.61504011);陕西省自然科学基金(No.2014JQ8344,No.2015JM6357);西安市科技计划项目(No.CXY1441(9));中央高校基本科研业务费(No.31083216002) TN32 A 0372-2112 (2016)07-1763-09 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.07.035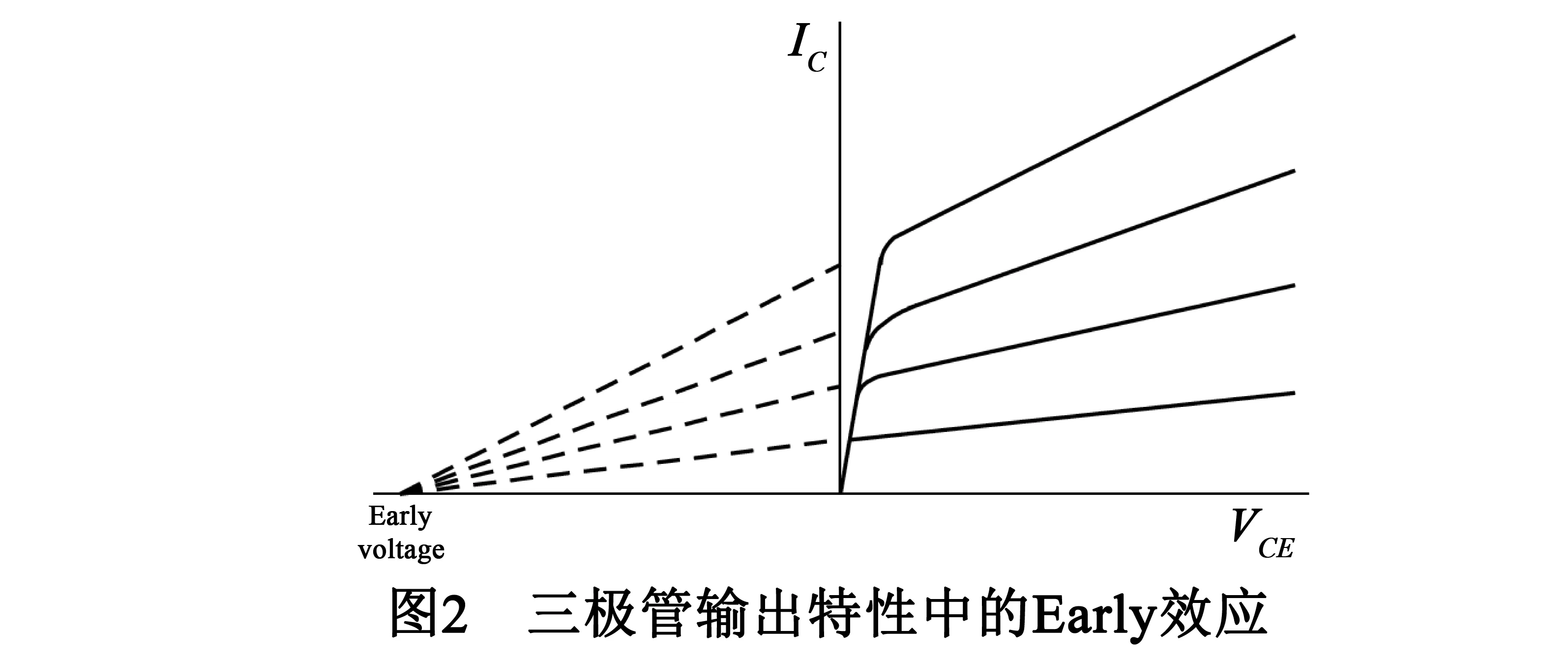
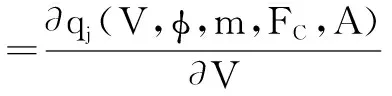

3 SiGe HBT与Mextram、HiCUM模型
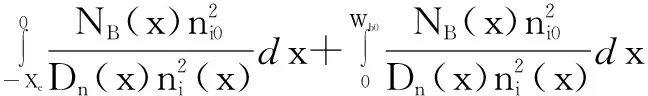

4 结论



