斜腿刚构桥的非线性动力特性分析

林本虎，　王赞芝

(广西科技大学土木建筑工程学院，广西 柳州 545000)



斜腿刚构桥的非线性动力特性分析

林本虎，王赞芝

(广西科技大学土木建筑工程学院，广西 柳州 545000)

摘要：以我国第一座钢斜腿刚构桥——安康汉江大桥为例，首先对结构进行了线性动力特性分析，得到了相应的结果。然后分别考虑轴向力和大挠度两种几何非线性因素对结构进行了非线性动力特性分析，并将计算得到的结果与线性理论结果进行比较分析，由此可以得出结论：安康汉江大桥所采用的线性计算理论已具有足够的精度，能够满足工程计算的要求。

关键词：斜腿刚构桥；轴向力；大挠度；非线性动力特性；线性理论

1 研究目的

随着科学技术的发展和人们认知水平的提高，许多学者开始关注结构中的非线性因素，这样就使得非线性问题出现在许多学科领域中。实践中，人们总希望能够用比较简单的线性计算模型来取代实际的非线性结构，以求方便地获得结构动力学行为的某种逼近。然而，被略去的非线性因素往往会在分析计算中导致很大的误差，从而使得线性分析结果失真。特别是对于经历长期荷载作用的结构，有时即使忽略很微小的非线性因素，也会在计算结果中出现实质性的错误。

斜腿刚构桥由于结构新颖、优美，具有很多独特的优点。自1953年西德建成霍勒摩尔跨线斜腿刚构桥之后，近几十年来，这种桥梁结构型式相继在许多国家出现。汉江斜腿刚构桥是我国首次采用的钢斜腿刚构结构型式。汉江斜腿刚构大桥由于结构纤细，为了对其刚度有充分的认识，对其进行动力特性分析必不可少。而像斜腿刚构桥这样的高次超静定结构又具有一定的非线性因素特征，因此，对斜腿刚构桥的非线性研究显得愈加紧迫。

2 工程概况

汉江单线斜腿刚构桥位于我国陕西省安康境内，其中梁主跨以56 m+64 m+64 m+64 m+56 m分跨，总长305.1 m，两斜腿铰中心距176 m，梁中心线至铰中心的高度为52.0 m。斜腿横向分成两肢，以6∶1坡度向两侧撑开，两肢之间有6根横杆相连，腿底部设铰支座，斜腿两肢铰中心距25.647 m。钢梁为薄壁箱型栓焊结构，钢材为国产50 kg级的16Mnq低合金钢，是一种可焊性能良好的钢种；高强度螺栓用40B钢制成，热处理后的极限强度1 150 MPa。全桥立面布置见图1所示。

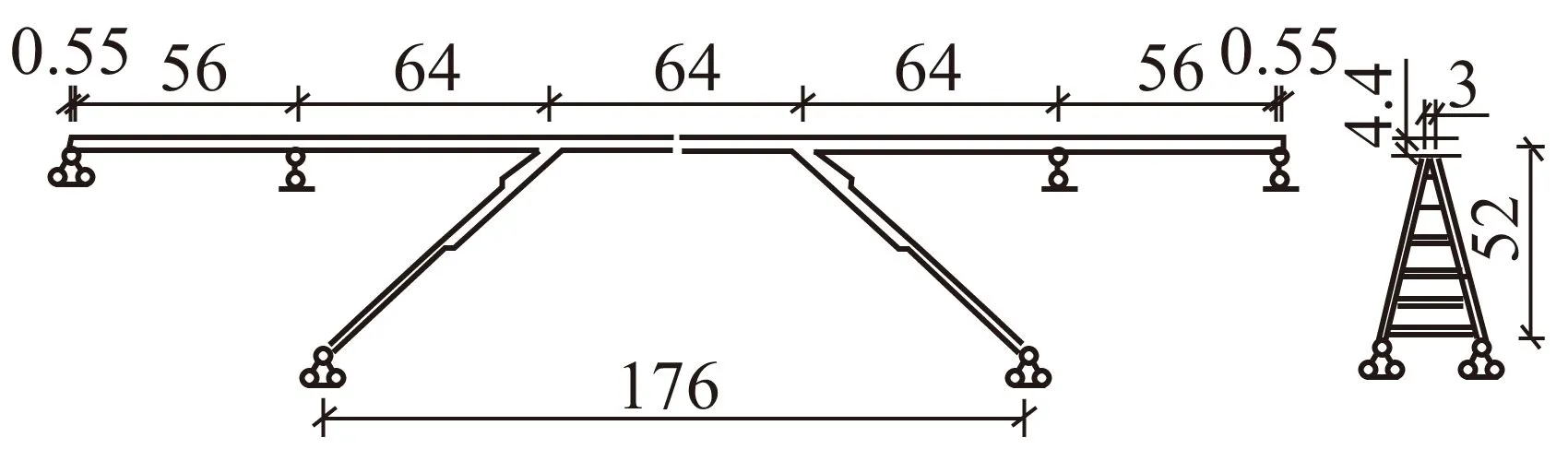
图1 汉江桥立面布置图(单位：m)

主梁为高4.4 m、宽3.0 m的矩形箱梁，腹板厚度：一般梁段为10 mm，支点附近的梁段为14 mm，隅节点处的梁段为20 mm，全梁断面等高，分成10～12 m长的梁段，每段分上下两层，在工厂焊接后发送工地组装。主梁每隔4 m设一横隔板，两横隔板之间每侧腹板设一根竖桥向加劲肋，支点附近剪力较大，设两根竖桥向加劲肋。上、下盖板各焊4根纵向加劲肋，间距为600 mm；每侧腹板沿高度各焊4根纵向加劲肋，中部设有一条拼接带。主梁截面如图2所示。

3 斜腿刚构桥线性动力特性分析

汉江斜腿刚构桥具有又长又窄又高的特点，所以其横向刚度如何，成了比较重要问题。同时结构动力分析是进行桥梁结构抗震分析的基础，因此在进行大跨度斜腿刚构桥抗震分析之前，首先需要进行振型分析，弄清楚结构的动力特性。根据该桥的动力特性，振型组合采用CQC法[1]。

图2 主梁断面图(单位：cm)

3.1 结构有限元模型的建立

现将斜腿刚构桥离散为78个空间梁单元，共71个节点，每个梁单元长8 m，斜腿刚构桥斜腿单元和横撑单元则按照实际情况变化，采用有限元软件Midas对结构进行计算，计算模型见图3所示。

图3 有限元计算模型

3.2 计算方法和原理

将结构划分成单元后，质量假定集中在节点上，形成一多自由度的弹性结构体系。振动时，体系离开静力平衡位置，此时，结构的弹性抗力，用矩阵符号表示为:

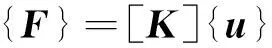
(1)

式中： [K]为结构刚度矩阵； {u}为节点位移列阵。

体系在振动过程中，质量m还受到一个惯性力I的作用，其值为：

(2)

在质量振动过程中的任何时刻，如果体系不再受到其他外力和阻尼力的作用，则这两个力总是相互平衡的。即

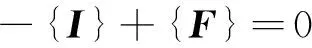
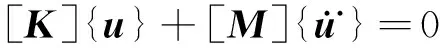
(3)

现在假设结构是在弹性阶段工作的，且属于小变形情况，略去阻尼的影响，自由振动将是简谐运动，于是各质量的位移和时间的函数关系，可用下式表示：

所以有

(4)

由此方程可以看出，结构的圆频率取决于质量分布、刚度分布及边界条件。利用迭代法，并应用振型的正交性可以求算出特征方程(4)的特征值及其相应的特征向量。

3.3 线性动力特性计算结果

根据前面所建立的空间模型，利用有限元结构软件对模型进行特征值分析，得到其自振周期和振型等动力特性参数，限于篇幅的关系，表1和图4只列出其前3阶自振周期及相应的振型。

表1 前3阶线性动力特性参数结果

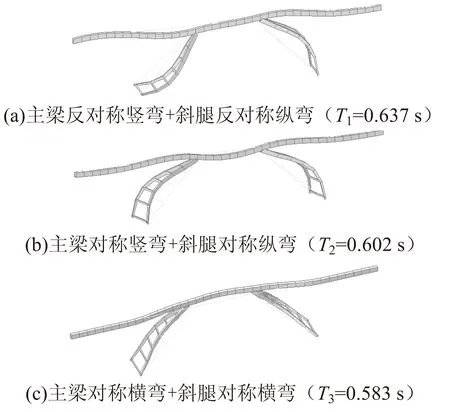
图4 线性动力特性计算振型图

4 斜腿刚构桥非线性动力特性分析

4.1 非线性因素的分析

众所周知，斜腿刚构桥具有拱的某些特点。在腿部及两腿之间的梁内具有较大的轴向压力，这种轴向压力将降低结构的弯曲刚度。同时，斜腿钢构结构轻巧、跨度较大，因此恒载作用下的挠度值也较大。考虑大挠度影响时，应按恒载变形位置去建立力的平衡关系，从斜腿刚构的上述特点出发，本论文研究讨论了轴向力和大挠度这两种几何非线性因素[2-3]对结构动力特性的影响。

4.2 非线性动力特性计算原理

对于线性弹性结构系统，矩阵位移法的基本方程是

(5)

式中：[Ke]为弹性刚度矩阵；{u}为节点位移矢量；{P}为节点荷载矢量。

一旦结构的材料性质、截面性质及离散后的节点坐标确定，[Ke]就唯一确定。

考虑非线性影响后，式(5)不再成立。这时，结构的刚度矩阵将与荷载历程有关，即与结构的内力和位移状态有关。对于几何非线性而言，结构刚度矩阵的形式为：

(6)

式中：[KE]为弹性刚度矩阵；[KG]为几何刚度矩阵，也叫初应力矩阵，它与结构的当前内力有关。

本论文采用荷载增量法进行计算。对每一步加载而言，[KE]和[KG]均为常矩阵，亦即假定结构刚度矩阵具有分段线性性质。在每一步加载完成后，按照节点位移修改节点坐标，以计入大挠度影响。

把每步加载得到的位移增量和内力增量叠加之后，就得到结构在恒载作用下的内力及变形。这时，可按结构的恒载变形状态建立它的刚度矩阵[K]。

形成结构质量矩阵之后，求解振动特征值问题

(7)

便可以得到结构的自振频率ωt及其相应的振型{φ}i(i=1,2,3,…,n)。

4.3 非线性动力特性计算方法

4.3.1 结构刚度矩阵的形成

对于线性振动结构，在振动过程中，其恢复力与变形成比例，即结构的刚度系数K保持常量。但在很多情况下，结构的恢复力不与其位移成比例，因而就出现了非线性振动问题。对于非线性系统通常可以将刚度矩阵[K]写成两部分：

[KG]是一个与结构的当前内力成比例的量。因此，几何刚度矩阵为计入内力影响后对弹性刚度矩阵的修正部分。

因此，基于上述思路，利用卡氏定理[4]可以推导空间梁单元的弹性刚度矩阵[KE]和几何刚度矩阵[KG]。

4.3.2 结构质量矩阵的形成

由单元质量矩阵组集结构质量矩阵[5]的方法，与组集结构刚度矩阵的方法一样。不过只有在进行动力分析时才用到质量矩阵，因而只需要组集一次即可。

4.4 非线性动力特性计算结果

众所周知，斜腿刚构桥属于超静定结构，这种结构在自重作用下会在斜腿及主梁跨中截面处产生较大的轴向力和位移，而这两种非线性因素都会对结构的刚度和质量矩阵产生影响，进而也会影响结构的动力特性。因此，为了准确分析这两种非线性因素对结构动力特性的影响，本文利用有限元软件分别对其进行了特征值分析[6-7]。限于篇幅的原因，表2和图5也仅列出了结构的前3阶自振周期及相应的振型结果。

5 结论

由上述结果可知，考虑轴向力和大挠度两种几何非线性因素后，结构的自振周期等动力特性参数结果与线性理论结果相比变化不大，相差幅度在5%以内，完全满足工程精度的需求；在振型方面，除了第3阶振型形状与线性理论结果相比有一定的差异以外，其余的第1阶和第2阶振型与线性理论结果相比都比较相似，这主要是由于纵横向刚度的不同造成的，由于纵横向刚度的不同，有时即使结构的自振频率只发生微小的变化，也都会对结构的空间振型产生较大的影响。

总之，从结构的自振频率和自振周期结果来看，可以认为汉江桥所采用的线性计算理论已经具有足够的精度，能够满足工程需要。

参考文献

图5 非线性动力特性计算振型图

[1]Anilk K.Chopra.Dynamics of structures[M].4版.

London:Prentice Hall,2012

[2]贾丽君,滕小竹,郭 瑞.超大跨度斜拉桥非线性因素影响分析研究[J].世界桥梁,2006(3):35-37

[3]霍学晋,许圣祥,韩立中.蝶形拱桥主梁的非线性行为及影响因素分析[J].公路交通科技,2014(5):57-65

[4]J.S.普齐米尼斯基.矩阵结构分析理论[M].北京:国防工业出版社,1975

[5]刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2012

[6]宗周红,赖苍林,林友勤.大跨度预应力混凝土连续刚构桥的动力特性分析[J].地震工程与工程振动,2004(3):98-104

[7]尹海军,李子青,郭 琦,等.大跨高墩连续刚构桥动力特性研究[J].西安建筑科技大学学报：自然科学版,2010(5):663-668

收稿日期：2016-03-11

作者简介：林本虎(1988—)，男，硕士研究生，研究方向为桥梁结构工程与抗震分析625883919@qq.com

DOI：10.13219/j.gjgyat.2016.04.009

中图分类号：U448.232

文献标识码：A

文章编号：1672-3953(2016)04-0033-04

An Analysis of the Nonlinear Dynamic Characteristics of a Slant-Legged Rigid-Frame Bridge

Lin Benhu，Wang Zanzhi

(Department of Civil Engineering and Architecture of the Guangxi University of Science and Technology,Liuzhou 545006,China)

Abstract:With the 1st steel slant-legged rigid-frame bridge in our country——the Hanjiang River Bridge in Ankang—as a practical example,the linear dynamic characteristics of the structure of the bridge is first analyzed in the paper,with the corresponding results obtained.Then,with the two geometric nonlinear dynamic factors of the axial force and great deflection respectively taken into account, the nonlinear dynamic characteristics of the structure are analyzed. Upon this basis,the calculated results thus are compared with those obtained by the linear theory, and both the results are also analyzed. From the above-mentioned comparison and analyses, it can be concluded that the linear calculation theory adopted for the calculations of the Hanjiang River Bridge in Ankang is already accurate enough to meet the requirements for engineering calculations.

Key words:slant-legged rigid-frame bridge；axial force；great deflection；nonlinear dynamic characteristics；linear theory