分类觅食人工鱼群算法
李 辉
(福建水利电力职业技术学院数学教研室, 福建 永安 366000)
分类觅食人工鱼群算法
李辉
(福建水利电力职业技术学院数学教研室, 福建 永安366000)
摘要:针对人工鱼群算法搜索速度和搜索精度不高,且对高维问题寻优能力较差等缺点,提出了一种改进的人工鱼群算法——分类觅食人工鱼群算法(Assorted Foraging Artificial Fish Swarm Algorithm-AFAFSA)。该算法对执行觅食行为的个体分类进行更新,既保持种群的多样性又通过觅食行为加快算法的搜索速度,同时加入禁忌的思想帮助算法跳出局部最优,提高算法的性能。通过一系列的测试试验,发现改进算法在收敛速度和精度方面都有了明显的提高,对于高维问题有也具有较好的寻优能力。
关键词:人工鱼算法;觅食行为;收敛速度;收敛精度
0引言
智能优化算法由于其广泛的适用性和良好的搜索效果,受到学者的广泛关注。人工鱼群算法是由李晓磊等[1,2]学者模拟鱼类行为提出的一种新的智能优化算法,该算法模拟鱼群的觅食、追尾等行为,实现全局优化,是群体智能思想的一个具体应用。基本的人工鱼群算法包括觅食、聚群、追尾3种行为,通过鱼群选择不同的行为搜索全局最优值。文献[1-3]的研究表明:对于较低维的问题,该算法可以很好的跳出局部极值、快速搜索到全局极值,并且该算法有很多的优点,比如对初始值和参数的选取要求不高,算法稳定性比较高,而且算法更新机制简单、易操作也方便改进以应用于实际问题。目前,该算法已经应用到许多领域。李晓磊[2]将其应用于求解连续函数的优化和组合优化问题;马建伟等[4]将其应用于神经网络的优化,取得较好的效果;王正初等[5]将人工鱼群算法应用于水库调度优化;王会颖等[6]将该算法应用于多维背包问题的求解,取得较好的结果。但是人工鱼群算法在实际应用中也存在着以下几点不足:1)当寻优区域较大或鱼群处于较集中的区域时,算法的全局收敛速度减慢、精度降低;2)算法在优化早期收敛速度较快,但是在优化后期搜索结果改善较慢,搜索速度较低;3)算法对于高维问题很难求得精确的最优解;4)相对粒子群等算法而言,计算复杂度有待进一步改善。
为了不断改善基本算法的性能,扩大算法的应用范围,很多学者对基本算法进行了改进,比如刘佳、刘丽娜、李靖等[7]将模拟退火算法融入鱼群算法进行改进;许恒迎、孙伟斌、张霞等[8]通过调整人工鱼的视野和步长改善鱼群算法的性能;祁俊、赵慧雅、李明等[9]通过混沌映射对鱼群进行初始化和扰动,增强群体的多样性;张严、楚晓丽[10]对鱼群算法的觅食行为和拥挤因子进行调整提高算法的性能。
1人工鱼群算法

1.1行为描述
1.1.1觅食行为
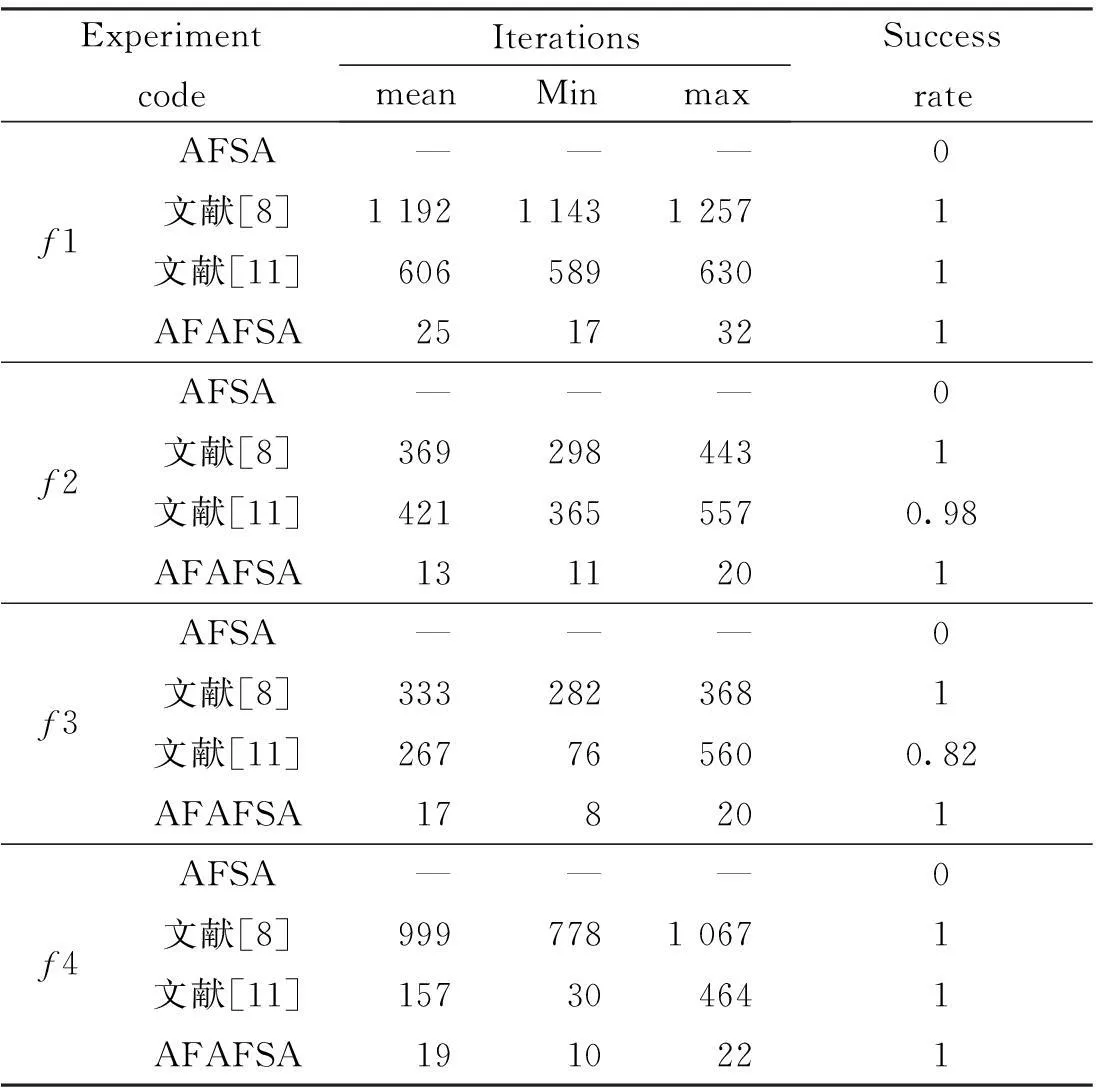
设个体鱼目前的位置为Xi,在其视野范围内随机选择一个位置Xj,若为求极小值优化问题,如果Yj (1) 其中,rand(s)为个体移动的步长。否则,重新选择一个位置Xj,判断是否满足移动条件;重复几次后,如果仍然不满足移动条件,则随机移动一步。 1.1.2聚群行为 设个体鱼当前所处的位置为Xi,寻找当前邻域内(即dij (2) 否则执行觅食行为。 1.1.3追尾行为 设人工鱼当前的状态为Xi,探索当前邻域内(即dij (3) 否则执行觅食行为。 1.2行为选择 按照需处理的问题的特征,对人工鱼当前的情况进行评估,经分析后选取其中的一种行为执行。比如求解最小值优化问题,最简单的评估方法就是试探法,即每次迭代中都分别试执行聚群行为和追尾行为,然后比较不同行为的结果,选择结果较好的、即目标函数值更小的行为来实际执行,缺省时即执行觅食行为。 2分类觅食人工鱼群算法 基本人工鱼群算法的觅食行为中,个体Xi在感知范围内随机走一步,若更好就向该方向前进一步,否则重新选择一个状态,尝试几次仍然不好,则随机移动一步,觅食行为是人工鱼群算法中非常重要的行为,直接影响了算法的搜索速度和精度,但基本算法中觅食行为机制较简单,个体移动速度较慢,会使算法性能受到影响。为了充分提高算法性能,在觅食行为中,对不同个体进行不同处理,并进一步提高个体移动速度,即个体Xi在感知范围内随机选择一个状态Xj,若效果更好,则个体直接移动到该新位置,否则,若该个体Xi不是当前全局最优个体Pb,则根据个体自身信息和当前全局最优个体信息按式(4)更新该个体位置,即: Xi=rand()×Xi+rand()×(Pb-Xi) (4) 其中,rand()为(0,1)之间的随机数。对于全局最优个体,在觅食行为中,随机移动一步,保持算法的多样性。 在行为选择中,缺省时执行的是觅食行为,算法不能较好的跳出局部极值,因此,当算法陷入局部极值,即算法的全局最优值连续T次没有发生变化时,则不执行追尾行为和聚群行为,而是连续N次执行觅食行为,让人工鱼自由游动,避免过于集中,帮助算法尽快跳出局部极值。 该算法的计算流程如下: Step1:初始化。在可行域内随机产生m个个体鱼,选取个体鱼之间的最大允许距离V,移动步长S,邻域内个体鱼数目nf,拥挤度因子δ;设定全局最优值连续未改变次数T和觅食行为执行次数N。 Step2:若全局最优解连续未改变次数小于或等于T,按式(2)和式(3)对鱼群个体进行聚群行为和追尾行为,选择两者效果好的最终执行,否则按式(4)执行觅食行为;若全局最优解连续未改变次数大于T,则连续N次执行觅食行为。记录当前全局最优值。 Step3:判断是否达到停机条件,若是,则停,输出最优解,否则转Step2。 3仿真实验 3.1试验设计 为了测试分类觅食人工鱼群算法的性能,研究选取4个常用的测试函数(如下表1所示),对基本人工鱼群算法和改进人工鱼群算法进行比较。其中:第一个和第二个函数为单极值函数,第三和第四个函数为多极值函数。它们的理论全局最优值都是0。 基本人工鱼群算法和改进人工鱼群算法都采用20个个体种群,最大全局迭代次数为200,参数设置如下:步长S=0.2,最大允许距离V=0.52,邻域内个体鱼数目nf=5,拥挤度因子δ=0.1,T=5,N=3。试验结果为独立运行20次后的平均值。 研究尝试从以下几方面对算法性能加以分析:(1)比较算法在收敛精度一定时的收敛速度;(2)比较算法在迭代次数一定时的收敛精度;(3)将本文算法的结果与相关文献中的结果进行对比。 表1 用于测试改进算法的函数 3.2试验结果及分析 3.2.1收敛精度固定时的搜索次数 根据表1中的收敛精度,将算法独立运行20次,记录每次运行达到要求精度的迭代次数,比较不同算法对4个测试函数寻优时的迭代次数如表2所示,其中min为最少迭代次数,max为最大迭代次数,mean为20次运行中迭代次数的平均值;Success rate为成功率,即达到目标精度的运行次数占实验总次数的比率。 从表2的数据可以看出,基本人工鱼算法对4个测试函数的搜索都无法达到表1给定的精度,即基本算法对于高维问题的寻优能力较差;文献[8]中的算法虽然对4个测试函数都可以成功搜索到目标精度下的最优值,但所需的迭代次数非常多;文献[11]中的算法对于4个测试函数的搜索成功率也较理想,但所需的迭代次数同样很大;而改进的分类觅食人工鱼算法对4个测试函数都有较高的搜索成功率,且所需的迭代次数相比较其它算法有了较大的减少。从总体上说,改进后的人工鱼群算法(AFAFSA)在收敛速度上有很大的提高。 表2 在目标精度下独立运行20次的迭代次数 3.2.2迭代次数固定时的收敛速度和精度 迭代次数固定为100次,4个测试函数的进化曲线如图1所示,为了方便观察,对函数f1,f2的适应度取对数后绘制进化图,为了防止产生对数无意义的现象,以10-6为最小值来限制适应度的对数值,绘制结果如图 (a),(b)所示;函数f3和f4 直接绘制100次迭代的进化图如图(c),(d) 所示。其中横轴为迭代次数,纵轴为适应度值(或适应度的对数值),2支曲线分别表示AFSA和AFAFSA对4个测试函数的进化曲线。 在上面(a),(b)两图中,由于函数f1和f2的适应度值数据跨度比较大,因此对适应度取以10为底的对数,方便观察。由图中的曲线可以看出,AFAFSA比AFSA在收敛精度和收敛速度上都有非常大的提高,AFSA对4个测试函数在30维下都搜索不到最优解,而AFAFSA对4个函数的搜索精度和搜索速度都非常好,说明AFAFSA算法搜索速度快且精度高,而且对于很多优化算法不能处理的高维问题也有非常好的搜索速度和精度。 图1 迭代100次时的收敛速度和精度Fig.1 The convergence speed and accuracy of 100 times'iteration 3.2.3与文献报道的数据比较分析 表3是本文中的算法在进化200次下,同文献[12]和[13]中提出的改进算法在30维下搜索到的平均最优值的比较,由表3可以看出,AFAFSA比文献中的算法有更高的收敛精度,且对函数3和4甚至可以搜索到理论最优值。 表3 一些改进粒子群算法性能比较 4结论 研究提出的改进人工鱼群算法,对鱼群算法中的觅食行为进行改进,充分利用觅食行为的自由性,加快个体移动速度,同时通过加强自由游动增强种群多样性,以提高算法搜索速度和精度。从实验结果可以看出:改进人工鱼群算法相对于基本人工鱼群算法和一些文献中的提出的算法,在搜索精度和速度上都有很大的提高。不论是对单极值函数还是对多极值函数,甚至高维问题,算法都有很好的寻优能力,并且该改进算法搜索机制简单,稳定性强,便于操作应用,总体来说,该算法性能较好、实用性很强。 参考文献: [1] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002(22):32-38. [2] 李晓磊.一种新型的智能优化算法——人工鱼群算法[D/OL].杭州:浙江大学, 2003:35-62[2013-11-12].http://www.cnki.net/KCMS/detail/detail.aspx?QueryID=1&CurRec=1&recid=&filename=2003051212.nh&dbname=CDFD9908&dbcode=CDFD&pr=&urlid=&yx=&v=MDA0OTFOclpFYlBJUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTHlmWnVkdEZ5N2dVTHpMVjEyN0hiTzlIOVA=. [3] 高尚,杨静宇.群智能算法及其应用[M].北京:中国水利水电出版社,2006. [4] 马建伟,张国立,谢宏,等.利用人工鱼群算法优化向前神经网络[J].计算机应用,2004,24(10):21-23. [5] 王正初,周慕逊,李军,等.基于人工鱼群算法的水库优化调度研究[J].继电器,2007,35,11(21):43-47. [6] 王会颖,倪志伟,陈祥生.基于鱼群算法的多维背包问题研究[J].安徽农业科学, 2011,39(10):6114-6117. [7] 刘佳,刘丽娜,李靖,等.基于模拟退火算法的改进人工鱼群算法研究[J].计算机仿真,2011,28(10):195-198. [8] 许恒迎,孙伟斌,张霞,等.自适应视野和步长的局部邻域人工鱼群算法[J].计算机工程与设计,2012,33(7):2815-2821. [9] 祁俊,赵慧雅,李明.基于双混沌映射改进的人工鱼群算法[J].计算机应用与软件,2012,29(9):230-233. [10]张严,楚晓丽.一种改进的人工鱼群算法[J].计算机系统应用,2011,20(5):199-201 [11]王国联,洪毅,赵付青,等.一种简化的人工鱼群算法[J].小型微型计算机系统,2009,30(8):1663-1667. [12]WANG L G,HONG Y,SHI Q H.Global edition artificial fish swarm algorithm[J].Journal of System Simulation,2009,21,12(23):7483-7502. [13]ZHAO P J,LIU S Y.Shuffled frog leaping algorithm for solving complex functions[J].Application Research of Computers,2009,26(7):2435-2437. 文章编号:1004—5570(2016)01-0093-05 收稿日期:2015-06-15 作者简介:李辉(1981-),女,讲师,硕士,研究方向:基础数学教学及智能优化算法方面的研究,E-mail:huili_0102@163.com. 中图分类号:O224 文献标识码:A Assorted foraging artificial fish swarm algorithm LI Hui (Fujian College of Water Conservancy and Electric Power,Yong’an, Fujian 366000,China) Abstract:As the search speed and accuracy of the basic artificial fish swarm algorithm is not high and the optimization for high-dimensional problems is poor, a new improved artificial fish swarm algorithm which is called assorted foraging artificial fish swarm algorithm is proposed. The algorithm updates individuals which implement the foraging behavior assorted. This can maintain the diversity of the population and accelerate the search speed of the algorithm. The taboo idea is also added to help the algorithm escape from local optima and to improve the performance of the algorithm. A series of tests reveal that the assorted foraging artificial fish swarm algorithm is better than basic artificial fish swarm algorithm in convergence velocity and convergence precision. It also has high optimization ability for high-dimensional problems. Key words:AFSA; foraging behavior; convergence velocity; convergence precision