LDGMI测试线圈等效电路模型研究

张建强，何林芳

(天水师范学院 电子信息与电气工程学院，甘肃 天水　741001)



LDGMI测试线圈等效电路模型研究

张建强，何林芳

(天水师范学院 电子信息与电气工程学院，甘肃 天水741001)

摘要：为便于理解纵向驱动巨磁阻抗(LDGMI)效应的物理机制，对HP4294A阻抗仪的驱动线圈进行了讨论，忽略线圈漏磁场(LMF)的影响，在低频信号下可将磁芯线圈等效为RL串联电路模型，在高频信号下可等效为RLC并联电路模型。

关键词：LDGMI；驱动线圈；RL串联；RLC并联

0引言

巨磁阻抗效应(GMI)是指磁性材料的交流阻抗随外加直流磁场的变化而发生显著变化的现象，受材料磁性能、磁结构、交流驱动场和外加磁场的影响，反映的是材料的交流弱场磁化随外加直流磁场变化的一种物理现象。自1992年Mohri[1]等第一次在Co基非晶合金丝中发现了巨磁阻抗效应后，由于GMI效应能实现磁电信号的转换，并具有灵敏度高、响应快和稳定性好等特点，所以在传感器和磁记录等工程技术领域具有巨大的应用潜能，特别是在研制灵敏度高、稳定性好、功耗低、微型化的磁敏传感器[2]方面应用广泛。此后，人们在非晶薄膜、非晶玻璃包裹丝、纳米晶合金带等材料中相继发现了GMI效应，以提高GMI效应和改善材料性能为目的，开展了深入而广泛的研究。

一般而言，GMI效应根据驱动方式的不同可分为2类：横向巨磁阻抗(Transverse Driven Giant Magneto-Impedance，简称TDGMI)效应，TDGMI采用横向驱动方式，使交变驱动电流直接通过被测试样产生环向或横向交变驱动场，其与外加直流磁场相互垂直，测试引线与试样间的焊接无疑是本驱动方式的难点；纵向驱动巨磁阻抗(Longitudinally Driven Giant Magneto-Impedance，简称 LDGMI)效应， LDGMI 效应是由华东师范大学杨燮龙等于1998年首次报道[3]，其特点是采用纵向驱动方式，即交变电流通过磁芯线圈产生交变驱动磁场作用于磁性材料，且交变驱动场和外加直流磁场平行，优点是避免了GMI 效应载流导体与被测试样间的焊接难题以及试样的焦耳热损耗等问题，同时LDGMI 效应获得了比横向驱动巨磁阻抗效应高2个数量级以上的灵敏度[4]。认为LDGMI 效应和TDGMI 效应的区别在于工作模式不同，而基本物理机制相同，在应用开发中两者各有优缺点，相互形成互补关系，而LDGMI 效应相比TDGMI 效应具有灵敏度更高、可靠性更高、适应性更灵活等优点，在新型磁敏传感器和高性能测量仪器中会发挥独特的优势。随着电子测量技术的迅速发展，其测量技术和方法呈现出多样性，如有电桥法、谐振法、伏安法、自动电桥平衡法等。在测量过程中，根据对测试参数的不同要求选择不同的测量方法，本文在室温和大气环境下，使用HP4294A型精密阻抗分析仪检测磁性材料的纵向驱动巨磁阻抗效应。由于LDGMI效应测试系统测量获得的阻抗为被测试样和测试驱动线圈的等效阻抗[3]，为了便于理解LDGMI效应的产生机理，讨论了LDGMI驱动线圈在高、低频信号下的等效电路模型。

1LDGMI测量原理

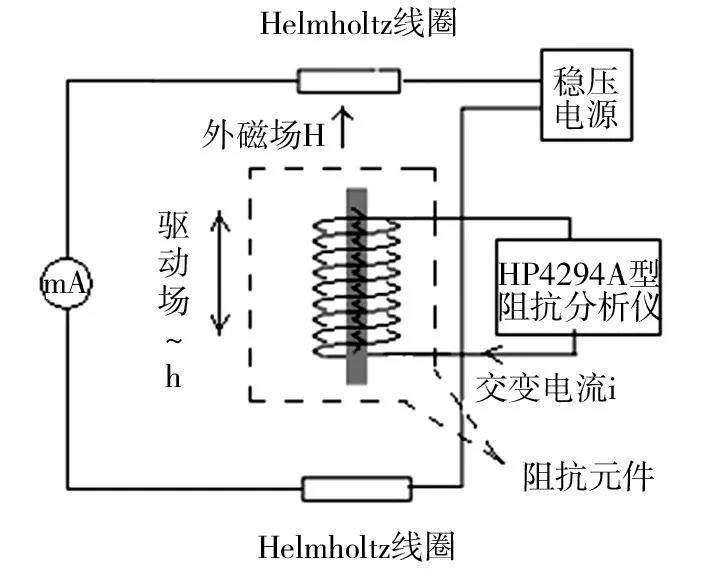
图1　GMI测试电路Fig.1　Test circuit of GMI

LDGMI效应的测量电路如图1所示，将检测试样放入密绕的驱动线圈中组成一个等效的阻抗元件。由HP4294A精密阻抗分析仪提供幅值10mA的交变电流通过驱动线圈，产生一个与试样轴向平行的交流驱动场，外加直流磁场由直径Φ=200mm的Helmholtz线圈(Helmholtz线圈由Φ=0.29mm漆包线绕制650匝而成)产生，方向沿试样的长轴方向，为减小地磁场的影响，直流外加磁场与地磁场方向垂直，测量时样品置于Helmholtz线圈中心均匀磁场区(其中心匀强磁场区的磁场强度公式Hex=58.446×I(Oe)，1Oe约为79.577 47Am-1)。通常情况下，巨磁阻抗比定义为：

(1)

式中ZHex和ZHmax分别表示任意外加直流磁场和最大磁场时的阻抗值。该测试系统中的HP4294A型阻抗仪采用自动电桥平衡技术，其基本原理如图2所示，可将平衡电桥看作一个放大器电路。被测试样通过一个交流源驱动，它的电压就是在高端H监测到的，低端L为“虚地”端，电压为0V，通过电阻器R2的电流I2跟通过被测试样的电流I1相等。因此，输出电压和通过被测试样的电流成正比，电压和电流自动平衡，这也就是它的名字的由来。在实际应用中，为了覆盖更加大的频率范围，通常用一个null-detector和modulator来代替电路中的放大器。

2测试线圈等效电路

该测试系统中的HP4294A型阻抗仪提供的交流驱动电流的频率范围为40Hz～110MHz，同一结构的磁芯材料，其LDGMI效应随频率具有很大的差别。为了减小线圈漏磁效应和分布电容的影响，密集绕制线圈并要求其尺寸和磁芯材料相当。本文忽略漏磁效应对线圈电磁参数的影响，讨论驱动磁芯线圈的等效电路模型。

2.1低频线圈等效电路模型

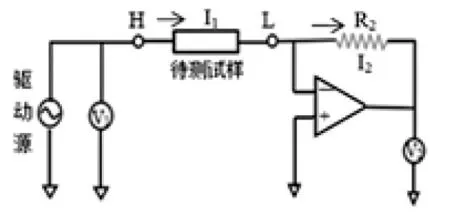
图2　HP4294A型阻抗仪原理电路图Fig.2　Circuit principle diagram of HP4294A impedance instrument

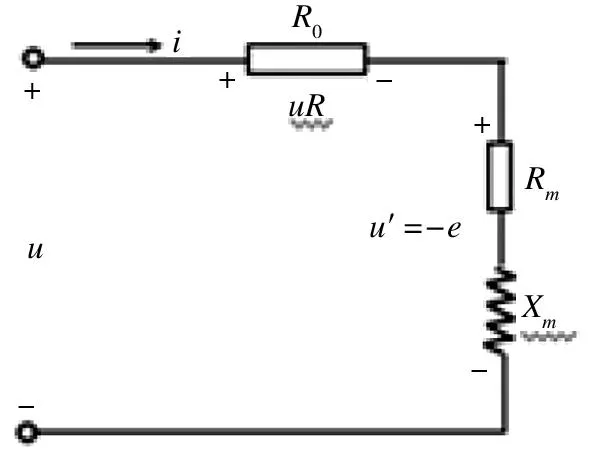
图3　低频线圈等效电路Fig.3　Effective circuit of low frequency coil

在低频(40Hz～2MHz)信号下，交变驱动电流通过磁芯线圈，在线圈中产生交变驱动场磁化磁芯材料，这种磁化行为在外加直流磁场的作用下进行。在此过程中，交变电流提供的电场能一部分转化为磁化磁芯材料的磁场能，而另一部分以热量的形式耗散，这部分耗散掉的能量主要来源于线圈电阻热效应和磁芯材料中的涡流损耗，又由于磁芯线圈具有较小的磁滞效应和较大的容抗，所以忽略磁滞损耗和分布电容的影响[5]。其等效电路模型如图3所示，将磁芯线圈等效为线圈导线直流电阻R0和没有电阻的理想磁芯线圈，但磁芯线圈中仍有能量的耗散(涡流损耗)和能量的储放，所以将理想的磁芯线圈交流电路用具有电阻Rm和感抗Xm的电路等效代替。其中R0为线圈铜导线的电阻，电流流过所产生的能量损耗称之为铜损，Rm是和磁芯材料中能量损耗(铁损)所对应的等效电阻，Xm是和磁性材料中能量的储放(与电源发生能量互换)相对应的等效感抗。由电路的基尔霍夫定律可知：

u=uR+u′=uR-e，

(2)

则电路阻抗为

Z=(R0+Rm)+jXm。

(3)

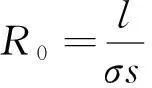
(4)

依电磁学原理，计算空芯线圈电感的经验公式为

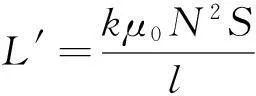
(5)

其中k为线圈半径与长度比值，μ0为真空磁导率，N为线圈扎数，S为其截面积。设磁芯材料截面积为Sm，所以含芯线圈电感为

Lm=kμ0N2(S-Sm)/l+kμ0μrN2Sm/lm=kμ0N2[(S-Sm)/l+μrSm/lm]。

(6)

若设线圈线绕密度n=N/l，则有：

Lm=kμ0n2[(S-Sm)l+μrSmlm]。

(7)

令A=kμ0n2(S-Sm)l，B=kμ0n2Smlm，低频线圈等效总阻抗

ZL=(L/σs+rlm)+jω(A+μrB)

(8)

当外加直流磁场Hex发生变化时，视线圈、磁芯材料的尺寸保持不变，则总阻抗的变化为

ΔZL=Δr+jωΔμr。

(9)

上式反映了磁芯材料直流电阻和磁导率随外加直流磁场的变化特性，即磁性材料的磁结构随外加磁场的变化而变化的物理机制。

2.2高频线圈等效电路模型

在高频(2MHz～110MHz)信号下，由于显著的趋肤效应，线圈磁芯的有效截面积减小，电阻值增大，此时线圈的分布电容不能忽略，其主要来源于以下几方面[7]：1)邻近线匝间分布电容；2)非邻近线匝间分布电容；3)线匝与磁芯之间分布电容；4)磁芯与地之间分布电容。如图4所示，将磁芯线圈等效为线圈电阻、磁芯涡流损耗等效电阻和理想线圈电感的串联，在其两端并联一个等效分布电容就是高频线圈等效电路模型。其等效阻抗表示为

(10)

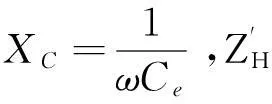
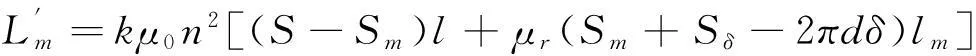
(11)

令Sδe=Sm+Sδ-2πdδ，其中Sm=πd2，Sδ=πδ2，将Sδe称为磁芯材料有效截面积，所以，

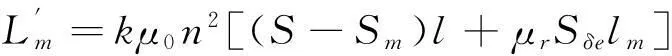
(12)

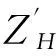
(13)

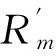
(14)

综上所述，在低频信号下可将LDGMI测试线圈等效为绕线电阻、磁芯涡流损耗等效电阻与理想磁芯线圈电感构成的RL串联电路模型；在高频信号下线圈可视为线圈绕线电阻、磁芯涡流损耗等效电阻与理想磁芯线圈电感构成的RL串联电路与线圈等效分布电容并联形成的RLC并联电路模型。

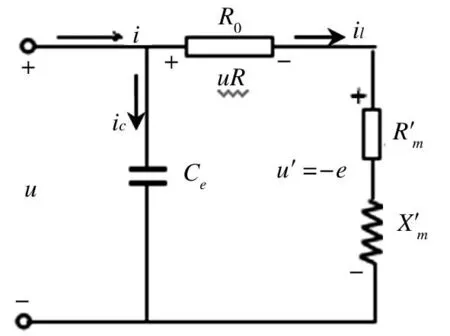
图4　高频线圈等效电路Fig.4　Effective circuit of high frequency coil

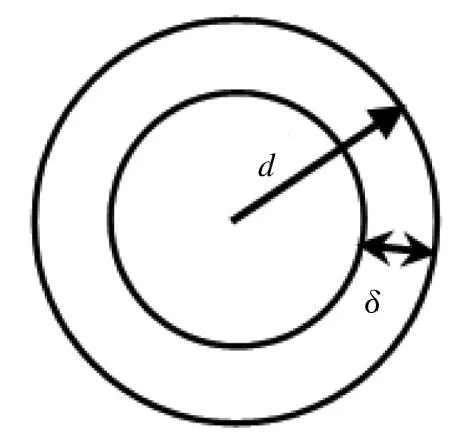
图5　磁芯材料截面Fig.5　Cross section of magnetic core materials

3结论

讨论了LDGMI测试驱动线圈的等效电路模型，在低频信号下可等效为RL串联电路模型来分析磁芯线圈特性，在高频信号下可等效为RLC并联电路模型，该电路模型的提出对解释纵向驱动GMI效应的产生机理有一定的理论指导意义。

参考文献：

[1] MOHRI K,KOHZAWA T,KAWASHIMA K,et al.Magneto-induced effect in amorphous wires[J].IEEE Transactions on Magnetics,1992,28(5):3150-3152.

[2] PHAN M H,PENG H X.Giant magneto-impedance materials: fundamentals and applications[J].Progress in Materials Science,2008,53(2):323-420.

[3] 杨介信,杨燮龙,陈国,等.一种新型的纵向驱动巨磁阻抗效应[J].科学通报,1998,43(10):1051-1053.

[4] 范晓珍,方允樟,何兴伟,等.纵向驱动巨磁阻抗效应的研究进展[J].浙江师范大学学报(自然科学版),2014,37(2):135-141.

[5] 秦增煌,韩三勇.电工学(上册)[M].第七版.北京：高等教育出版社,2009:196-197.

[6] 方允樟,许启明,郑金菊,等.FeCo基磁芯螺线管巨磁阻抗效应与磁芯长度关系的研究[J].物理学报，2011,60(12):127501-6.

[7] 袁义生.电感器分布电容的建模[J].华东交通大学学报,2006,23(5):90-93.

文章编号：1004—5570(2016)01-0077-04

收稿日期：2015-09-10

基金项目：天水师范学院中青年教师科研资助项目(No.TSA1324)

作者简介：张建强(1983-)，男，讲师，硕士，研究方向：磁性材料及器件，E-mail:zhjian8386@163.com.

中图分类号：TM12

文献标识码：A

A equivalent circuit model for measurement coil longitudinal driven giant magneto-impedance effect

ZHANG Jianqiang,HE Linfang

(School of Electronic Information and Electrical Engineering, Tianshui Normal University, Tianshui, Gansu 741001, China)

Abstract:For ease to understand the mechanism of longitudinal driven giant magneto-impedance (LDGMI) effect,a driven coil of HP4294A impedance instrument is discussed.Ignore the influence of leakage magnetic field (LMF),we suggest that at the low frequency range,the coil can be equivalent to RL series circuit model, but at the high frequency range, it can be equivalent to RLC parallel connection circuit model.

Key words:LDGMI; driven coil; RL in series model; RLC parallel model