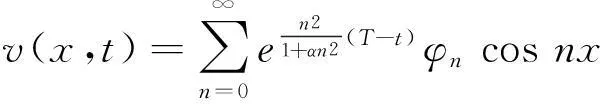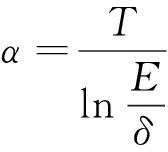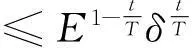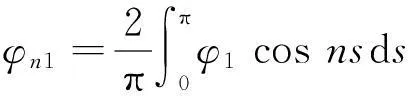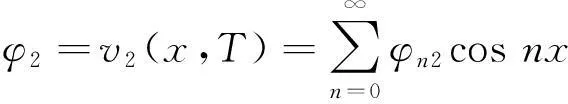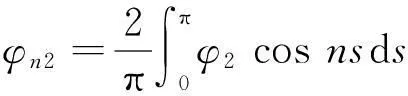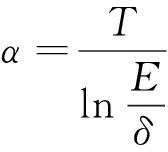反向热传导问题的拟可逆正则化方法

刘利平

(甘肃政法学院 信息工程学院，甘肃 兰州　730070)



反向热传导问题的拟可逆正则化方法

刘利平

(甘肃政法学院 信息工程学院，甘肃 兰州730070)

摘要：反向热传导问题是一类严重的不适定问题，它给数值处理带来了很大的不便。通过拟可逆正则化方法，恢复了解对数据的连续依赖性，并给出误差估计。通过提高先验光滑性假设得到了t=0时的收敛性。

关键词：反向热传导问题；不适定问题；拟可逆方法；误差估计

0引言

由热导体在某一时刻t=T>0时的温度测量值来确定物体在0≤t

考虑如下反向热传导问题：

(1)

以下用‖·‖和(·)分别表示L2(R)空间中的范数和内积，本文将通过拟可逆正则化方法，恢复解对数据的连续依赖性。

对方程(1)利用分离变量法得到该问题的精确解为：

(2)

‖w(·,0)‖≤E

(3)

1拟可逆正则化及其误差估计

考虑对应于问题(1)，正如文献[9,10]提出的问题：

(4)

同样利用分离变量法可以求得问题(4)解的为：

(5)

(6)

证明由(5)式，有

(7)

(8)

由‖φ1-φ2‖≤δ，即

(9)

(10)

于是可以得到

‖v1(·,t)-v2(·,t)‖2

(11)

(12)

证明由(3) (5)式，有

(13)

和

‖w(·,t)-v(·,t)‖=

(14)

(15)

注意到(n2-θ2)(T-t)≥0,n=0,1,2,…，于是

利用不等式1-e-r≤r(r≥0)可得

A(n)≤e-n2t(n2-θ2)(T-t)

(16)

(17)

于是A(n)≤e-n2tn4α(T-t)，对于函数h(n)=e-n2tn4，令h′(n)=0求得其最大值为：

(18)

从而得到这一节的主要结果。

(19)

证明设v(·,t)是由(5)式给出的问题(4)对应于精确数据φT(x)的解，则

‖w(·,t)-vδ(·,t)‖≤‖w(·,t)-

v(·,t)‖+‖v(·,t)-vδ(·,t)‖。

(20)

结合定理1，定理2以及式子 (13)，(20)可以得到估计(19)。

2零点处理

然而注意到当t=0时上面的收敛性将不再成立。因而为了得到t=0时正则解的收敛性，我们务必需要更强的先验假设条件：

(21)

其中p>0为整数。

(22)

(23)

设v(·,0)是由式(5)给出的问题(4)对应于精确数据φT(x)的解。由(2)和(5)式有：

‖w(·,0)-vδ(·,0)‖≤‖w(·,0)-v(·,0)‖+‖v(·,0)-vδ(·,0)‖

(24)

(25)

(26)

当n≥1时，分情况考虑如下2种情况：

(27)

(28)

(29)

(b)当p≥2，注意到n2≥1有B(n)≤αT。

(30)

综合(27)、(28)、(29)以及(30)式，容易得到

(31)

结合(24)、(25)和(31)式，就得到了(22)。

(32)

3小结

反向热传导问题是一类严重的不适定性问题，已经出现了大量的方法用来解决此问题。研究考虑了利用拟可逆正则化方法去解决这个问题，恢复了解对初始数据的连续依赖性。

参考文献：

[1] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005:108-109.

[2] PAYNE L E.Improperly posed problems in partial differential equations[C/OL]. Philadelphia: SIAM,1975,187-189.[2015-08-25].https://books.glgoo.com/books?hl=zh-CN&lr=&id=JgmRU0DO2soC&oi=fnd&pg=PP2&dq=Improperly+posed+problems+in+partial+differential+equations&ots=Xgdq9TItIM&sig=b7uZKf7WKvoe2HjE_67h6G9udZc&redir_esc=y#v=onepage&q=Improperly%20posed%20problems%20in%20partial%20differential%20equations&f=false.

[3] HADAMARD J.Lectures on Cauchy’s problem in linear partial differential equations[M/OL].Courier Corporation,New Heavens:Yale University Press,2014,96-97.[2015-08-22].https://books.glgoo.com/books?hl=zh-CN&lr=&id=9RNeBAAAQBAJ&oi=fnd&pg=PA3&dq=Lectures+on+Cauchy+problems+in+linear+partial+differential+equations&ots=EpbmEem6iM&sig=5MKE0tKkJi8_dixvp_2cdSZS0PQ&redir_esc=y#v=onepage&q=Lectures%20on%20Cauchy%20problems%20in%20linear%20partial%20differential%20equations&f=false.

[4] MERA N S,ELLIOTT L,INGHAM D B,et al.An iterative boundary element method for solving the one dimensional backward heat conduction problem[J].International Journal of Heat and Mass Transfer,2001,44(10):1973-1946.

[5] MIRANKER W L.A well posed problem for the backward heat equation[J].Proceedings of the American Mathematical Society,1961,12(2):243-247.

[6] LESNIC D,ELLIOTT J,INGHAM D B.An iterative boundary element method for solving the backward heat conduction problem using an elliptic approximation[J]. Inverse Problems in Engineering,1998,6(4):255-279.

[7] LIU C S.Group preserving scheme for backward heat conduction problems[J]. International Journal of Heat and Mass Transfer,2004,47(12):2567-2576.

[8] JOURHMANE M,MERA N S.An iterative algorithm for the backward heat conduction problem based on variable relaxation factors[J].Inverse Problems in Engineering，2002,10(4):293-308.

[9] QIAN Z,FU C L,XIONG X T.Fourth-order modified method for the Cauchy problem for the Laplace equation[J].Journal of Computational and Applied Mathematics,2006,192(2):205-218.

[10]KIRSCH A.An introduction to the mathematical theory of inverse problem[M/OL].Springer Science & Business Media,2011,110-112. [2015-09-03].https://books.glgoo.com/books?hl=zh-CN&lr=&id=RTo9ZFaSSugC&oi=fnd&pg=PR3&dq=An+Introduction+to+the+Mathematical+Theory+of+Inverse+Problem&ots=hOWY_HHIn2&sig=aNlhPmZu0jlCl2nNcy-cfAGUl1k&redir_esc=y#v=onepage&q=An%20Introduction%20to%20the%20Mathematical%20Theory%20of%20Inverse%20Problem&f=false.

文章编号：1004—5570(2016)01-0073-04

收稿日期：2015-10-06

作者简介：刘利平(1984-)，女，讲师，理学硕士，研究方向：数学物理反问题理论及计算研究，E-mail: 13494766@qq.com.

中图分类号：O551.3；O175

文献标识码：A

The perturbation method for a backward heat equation

LIU Liping

(School of Information Engineering, Gansu Institute of Political Science and Law University,Lanzhou, Gansu 730070, China)

Abstract:The backward heat conduction problem (BHCP) is a severely ill-posed problem and it seems impossible to compute numerically on the data does not depend the solution when it continuously. In this paper, the stability of this problem is recovered by a perturbation method and the error estimates is given. The other improved by prior smoothness assumptions.

Key words:backward heat conduction problem; ill-posed problem; the perturbation method; error estimate