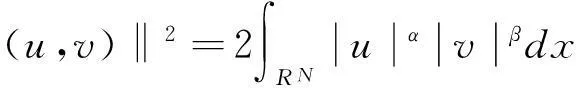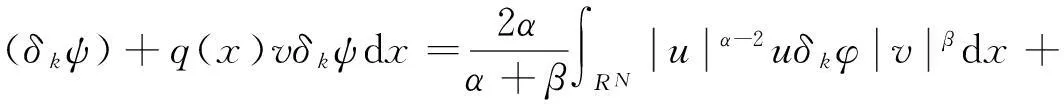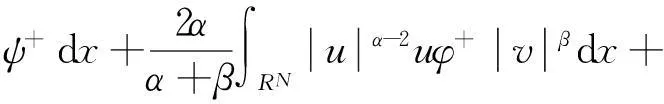全空间中椭圆方程组解的存在性

郝悦斌,李鸿翔

(山西大学 数学科学学院,山西 太原　030006)



全空间中椭圆方程组解的存在性

郝悦斌,李鸿翔

(山西大学 数学科学学院,山西 太原030006)

摘要：研究了下面椭圆方程组解的存在性问题

通过Nehari流形法证明了以上方程组具有非平凡解。

关键词：椭圆方程组;能量泛函;Nehari流形

0引言

在这篇文章中，我们主要研究RN(N≥3)中，以下一类椭圆方程组非平凡解的存在性问题

(1)

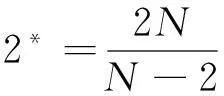
20世纪80年代，Mckenna和Walter提出了悬索桥的一维振动模型方程，通过分析，此模型的研究可归结为研究一类非线性椭圆方程(方程组)的问题。为此，许多学者投入到它的研究当中，而且许多重要的成果已经被证明。当α=β，u=v时，则(1)将简化为椭圆方程问题，即

(2)

(3)

许多学者也在不同条件假设下进行了研究。对于与(3)类似的研究可以参考文献[6-13]及其相关文献。例如，当q=0时，方程组(3)将转化为下面的形式

(4)

Mitidieri在文献[7]中在具体了f,g的函数形式时，证明了(4)存在有界的径向古典解。而Ma和Liu在文献[8]中通过应用Alexandrov-Serrin的移动平面方法进一步证明了(4)的衰弱正解关于一些点径向对称的性质。而当q=1时,方程组(3)将转化为

(5)

李工宝和王春花在文献[9]中通过对f,g进行了适当假设并证明了(5)至少存在一个正解。而对于f,g是自治的这一类问题,我们可以在拥有紧性的径向对称函数空间中研究，如文献[10，11]。

进行了讨论，作者首先对a(x)，b(x)进行适当的衰退假设，通过临界点理论，在有界球内找到近似解，通过分析近似解的结构并取极限，证明了方程组(6)有无穷多的正能量解。由于我们是在RN上进行研究，因此我们可能会遇到紧性缺失的问题。在前面相关文献的启发下，我们在本文将给出一个关于q的不同假设来解决紧性缺失这一问题，并证明在这一假设下(1)解的存在性。首先给出q的假设：

(Q):infx∈RNq(x)≥0

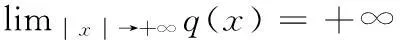
我们的主要结果如下：

定理1假设N≥3，α>1，β>1，α+β∈(2,2*)，且q满足假设Q，则问题(1)存在非平凡解。

1预备知识

定义H1(RN)的子空间X如下：

易知x仍是希尔伯特空间，而且可以在x上定义新的内积为：

(u1,u2)=∫RN▽u1·▽u2+q(x)u1·u2dx

∀u1,u2∈X，对应的范数为：

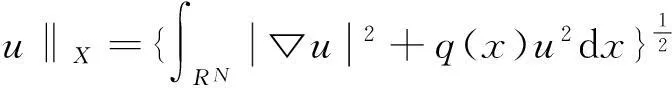
现在考虑空间Y=X×X，则Y也是一个希尔伯特空间，对应的范数为：

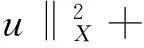
∀(u,v)∈Y。我们将在空间Y上对问题(1)进行研究。首先其对应的能量泛函为：

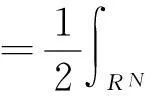
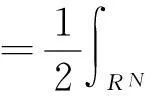
(u,v)∈Y。问题(1)的一个弱解就相当于泛函I(u,v)的一个临界点,也就是说对任意的(φ,ψ)∈Y都有

〈I′(u,v),(φ,ψ)〉=0

成立。即对(u,v)∈Y任意的(φ,ψ)∈H1(RN)×H1(RN)都有

(7)

对于对于泛函I(u,v)来说，容易知道I没有下界，因此我们将把I限制到Nehari流形上，其定义如下：

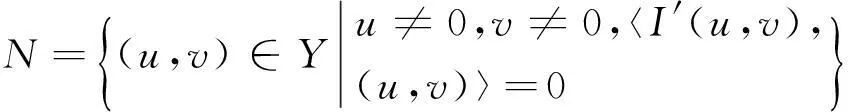
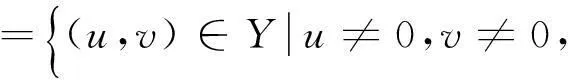
如果 (u,v)∈N，则相应的能量泛函为

(8)

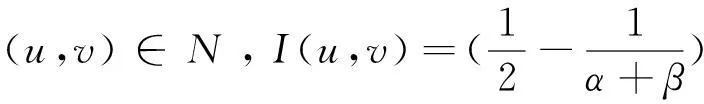
定义m=inf(u,v)∈NI(u,v)

2定理1的证明

引理1对于所有的p∈[2,2*)，X到LP(RN)的嵌入是紧嵌入。

证明证明过程可以参考文献[15]引理3.2.1。

引理2N是非空集。

容易解的

引理2得证。

引理3m>0成立。

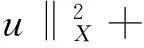
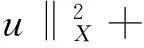
(9)

因此,从(9)可知

1≤C‖(u,v)‖α+β-2

所以,对于所有的(u,v)∈N，我们有

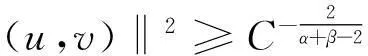
(10)

由上可知，当(u,v)∈N，有

成立。因此，引理3得证。

引理4存在(u,v)∈N，使得I(u,v)=m。

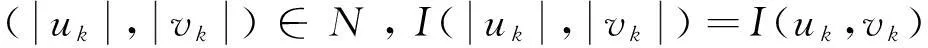
已知I(uk,vk)→m且有(8)成立，所以在X中{uk}k，{vk}k有界，即存在子列，不失一般性，仍将其定义为{uk}k，{vk}k使得在X中有uk弱收敛到u，vk弱收敛到v。由于α+β∈(2,2*)，由引理1可知在Lα+β(RN)

uk→u，vk→v

而且当x∈RN时

uk(x)→u(x)a.e.，vk(x)→v(x)a.e.

通过文献[16]引理A.1，我们还可知存在w1,w2∈Lα+β(RN)使得对于所有的k，在x∈RN有

由上可知x∈RN时，

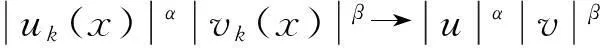
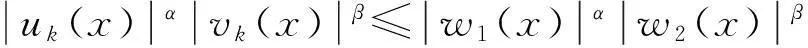
成立。通过应用Hölder不等式

因为w1,w2∈Lα+β(RN)，则函数

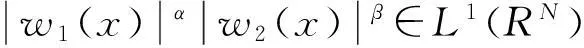
下证(u,v)∈N，且有I(u,v)=m。

首先，由(10)知

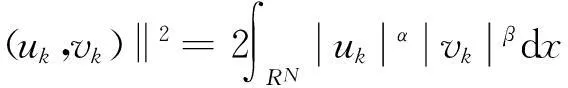
(11)

因此当k→∞时，

这表明了u≠0，v≠0。而从(11)我们还可得

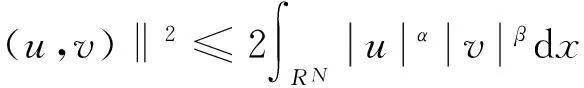
否则

(12)

在这种情形下，由引理2知，存在t>0使得 (tu,tv)∈N，这时

由(12)式知，t∈(0,1)。这时，我们有

0≤m≤I(tu,tv)

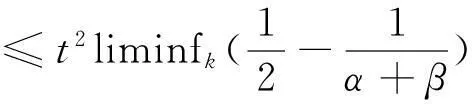
=t2liminfkI(uk,vk)=t2m

这一矛盾说明了

I(u,v)≤liminfkI(uk,vk)=m

引理4证毕。

引理5假设(u,v)∈Y，u≥0，v≥0是由引理4找到的极小值点，则(u,v)是I的临界点,即对任意的(φ,ψ)∈Y满足(7)式。

证明首先因为(u,v)是由引理4找到的极小值点,则(u,v)∈N。然后假定(φ,ψ)∈Y并且ε>0使得对任意的s∈(-ε,ε)，有

u+sφ≠0，v+sψ≠0

由引理2知，存在

使得t(s)(u+sφ,v+sψ)∈N。显然，函数t(s)是由可微函数构成，因此它是可微的，但t′的具体表达在证明中是无关紧要的。因为(u,v)∈Y，易知t(0)=1。显然的，映射

s|→t(s)(u+sφ,v+sψ)是定义在N上的一条曲线。接下来在其上估计I,定义γ:(-ε,ε)→R通过

γ(s)=I(t(s)(u+sφ,v+sψ))

由γ(s)的构造知，当s=0时,可以取到γ的最小值。因此

0=γ′(0)=〈I′(t(0)(u,v)),t′(0)(u,v)+t(0)(u+φ,v+ψ)〉

=(t′(0)+1)〈I′(u,v),(u,v)〉+〈I′(u,v),(φ,ψ)〉=〈I′(u,v),(φ,ψ)〉

由 (u,v)∈N得〈I′(u,v),(u,v)〉=0所以最后一行等式成立.因此我们得到了对任意的(φ,ψ)∈Y都有

〈I′(u,v),(φ,ψ)〉=0成立,即(u,v)满足(7)式.引理5证毕。

引理6如果对任意的(φ,ψ)∈Y，(u,v)满足(7)式，则对任意的(φ,ψ)∈H1(RN)×H1(RN)，(u,v)满足(7)式。

证明假定(φ,ψ)∈H1(RN)×H1(RN)且有φ≥0，ψ≥0。令{δk}k是一个C∞函数列且对任意x满足

0≤δk(x)≤1

易证

(δk(x)φ,δk(x)ψ)∈H1(RN)×H1(RN)且当k→∞时

(δk(x)φ,δk(x)ψ)→(φ,ψ)

上述强收敛在空间

Lα+β(RN)×Lα+β(RN)仍成立。因为q是局部有界的,(δk(x)φ,δk(x)ψ)具有紧支集，则(δk(x)φ,δk(x)ψ)∈Y成立。因此

(13)

通过强收敛可知

limk∫RN▽u▽(δkφ)dx=∫RN▽u▽φdx

limk∫RN▽v▽(δkψ)dx=∫RN▽v▽ψdx

因此由(13)可得

另一方面，对任意的k和几乎每一个x都有

0≤q(x)(uδkφ+vδkψ)

≤q(x)(uδk+1φ+vδk+1ψ)

利用BeppoLevi's单调收敛定理可知

limk∫RNq(x)(uδkφ+vδkψ)dx

=∫RNq(x)(uφ+vψ)dx

总之，我们可得：当

(φ,ψ)∈H1(RN)×H1(RN)，φ≥0，ψ≥0时，下式成立。

(14)

而对任意(φ,ψ)∈H1(RN)×H1(RN)，因为φ+≥0，φ-≥0，ψ+≥0，ψ-≥0则(φ+,ψ+)，(φ-,ψ-)满足(14)式,即

(15)

及

(16)

成立。因为有φ=φ+-φ-，ψ=ψ+-ψ-，用(15)-(16)可得，对任意(φ,ψ)∈H1(RN)×H1(RN)有(7)式成立。

由引理5和引理6可得到定理1的证明。

参考文献：

[1]BAHRIA,LIONSPL.Ontheexistenceofapositivesolutionofsemilinearellipticequationsinunboundeddomains[J].AnnInstH.Poincar’eAnalNonLinéaire,1997(14):365-413.

[2]BARTSCHT,WANGZQ.SignchangingsolutionsofnonlinearSchrödingerequations[J].TopolMethodsNonlinearAnal,1999(13):191-198.

[3]COTIZelatiV,RabinowitzP.HomoclinictypesolutionsforasemilinearellipticPDEinthewholespace[J].CommPureApplMath,1992(10):1217-1269.

[4]CERAMIG,DEVILLANOVAG,SOLIMINIS.Infinitelymanyboundstatesforsomenonlinearscalarfieldequations[J].CalcVarPartialDifferEqu,2005(23):139-168.

[5]ADIMURTHYF,PACELLAL,YADAVA.OnthenumberofpositivesolutionsofsomesemilinearDirichletproblemsinaball[J].DifferIntegralEqu,1997,10(6):1157-1170.

[6]CLEMENTP,FIGUEIREDO,MITIDIERIE.Positivesolutionsofsemilinearellipticsystems[J].CommPartialDifferEqu,1992(17):923-940.

[7]MITIDIERIE,Non-existenceofpositivesolutionsofsemilinearellipticsystemsinthewholespace[J].DifferentialIntegralEquations,1996(9):465-479.

[8]MAL,LIUB.Symmetryresultsfordecaysolutionsofellipticsystemsinthewholespace[J].Math,2010(225):3052-3063.

[9]LIG,WANGC.TheexistenceofnontrivialsolutionstoasemilinearellipticsystemsinthewholespacewithouttheAmbrosetti-Rabinowitzcondition[J].ActaMathematicaScientia，2010,30B(6):1917-1936.

[10]SIRAKOVB.OntheexistenceofsolutionsofHamiltonianellipticsystemsinthewholespace[J].AdvDifferEqu,2000(5):1445-1464.

[11]FIGUEIREDOD,YANGDG,DECAYJ.Symmetryandexistenceofsolutionsofsemilinearellipticsystems[J].NonlinearAnal,1998(33):211-234.

[12]LIG,YANGJ.Asymptoticallylinearellipticsystems[J].CommPartialDifferEqu,2004(29):925-954.

[13]AVILAAI,YANGJ.Multiplesolutionsofnonlinearellipticsystems[J].NonlinearDifferEquAppl,2005(12):459-479.

[14]LIUZ.InfinitelymanySolutionsforsomenonlinearscalarsystemoftwoellipticequations[J].MathAnalAppl,2011(382):731-747.

[15]BADIALEM,SERRAE.SemilinearEllipticEquationsforBeginners[M].NewYork:Springer-Verlag,2011:105-106.

[16]WILLEMM,MinmaxTheorems[M].Boston:Birkhäuser,1996:133.

文章编号：1004—5570(2016)01-0040-05

收稿日期：2015-10-22

基金项目：国家自然科学基金资助项目(61374089);山西自然科学基金资助项目(2014011005-2)

作者简介：郝悦斌(1989-),男,硕士研究生,研究方向:非线性泛函分析,E-mail:980223427@qq.com.

中图分类号：O175.25

文献标识码：A

Existence of solutions for elliptic system in the whole space

HAO Yuebin,LI Hongxiang

(School of Mathematical Sciences,Shanxi University,Taiyuan,Shanxi 030006,China)

Abstract:By using the method of Nehari manifold,we are able to obtain the existence of nontrivial solutions for the following elliptic system.

Key words:elliptic system; energy functional; Nehari manifold