基于牛顿迭代法的分形图像研究
任 露, 黄颖为
(西安理工大学 印刷包装与数字媒体学院, 陕西 西安 710048)
基于牛顿迭代法的分形图像研究
任露, 黄颖为
(西安理工大学 印刷包装与数字媒体学院, 陕西 西安 710048)
通过调用牛顿迭代法绘制分形图像,利用绘图参数和运算法则构造着色方案,研究复平面分形图像结构特征并提供多个新的着色方案,发现复平面分形图像结构有规律可循,图像色彩难以揣测。
牛顿迭代法; 分形图像; 结构特征; 着色方案
分形[1],通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”。即分形具有自相似特征,可利用计算机迭代来生成。牛顿迭代法作为计算机迭代的主要方法之一,绘制的分形图像结构具有对称性且有一定规律可循,图像像素点色彩和迭代次数相对应。相比于实数迭代分形集,在二维平面上,牛顿迭代法生成的复迭代分形集结构更加复杂,色彩更加丰富,包含更多信息,也具有更强的防伪特征[2-3]。本文利用牛顿迭代法绘制基于复迭代公式f(Z)=Zn-1(其中Z为复平面上的点,n为实数且n≥2)的广义Julia集,研究实数n对图像结构的影响,迭代参数及迭代参数与运算符的组合方式对图像色彩的影响,为实现分形图像的个性化和多样化设计提供参考。
1 牛顿迭代法绘制复平面分形图像
根据牛顿迭代法[4]求解复平面方程f(Z)=0,f(Z)的牛顿迭代函数为:
(1)
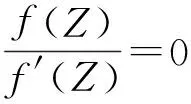
(2)
此时f(Z)的零点也是φ的超吸引不动点。当|Z|较大时,φ(Z)~Z(1-1/n),n为f(Z)的阶,∞是f(Z)的斥性点,则记A(ω)={Z0:φ(Zk)→ω},其中A(ω)表示零点ω的吸引域,即在牛顿迭代法下收敛于ω的初始点集。
牛顿迭代法绘制复平面分形图像的流程[5]如图1所示。首先设置迭代方程,然后在复平面上选择一点Z0作为迭代初始点,再进行着色处理,最终生成分形图像。
具体过程[6]如下。
设显示器的分辨率为A×B点,可显示的颜色为k+1种,分别用0,1,2,…,k表示。
1) 设置迭代方程f(Z)=zn-1中n的取值;
2) 选择绘图区域坐标xmax=2,ymax=1.5,xmin=-2,ymin=-1.5,设当前迭代次数为M,最大迭代次数为N,迭代精度为ε,dx=(xmax-xmin)/(A-1),dy=(ymax-ymin)/(B-1);
3) 设定迭代初始点值Z0=x0+y0i,x0=xmin+mx*dx,y0=ymin+my*dy,其中mx=0,1,…,A-1,my=0,1,…,B-1。
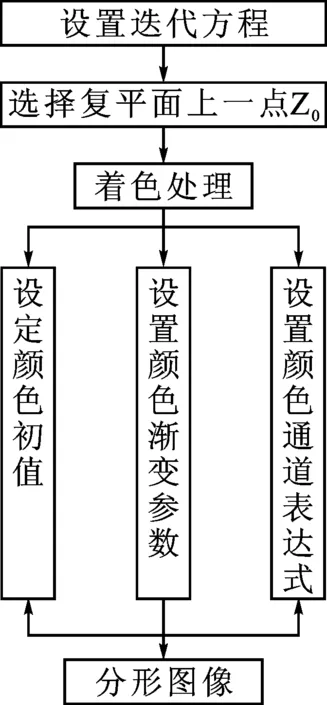
图1 分形图像绘制流程Fig.1 The procedure of fractal images generated
对所有点作如下循环:
for (x=0;x for (y=0;y { xk=xmin+x*dx; yk=ymin+y*dy; M=0; do { mod=|Zk+1-Zk|; Zk+1=Zk;k++; } while (mod≥ε&&k if (mod<ε)用颜色k显示点(xk,yk); else if (M==N)用某一固定颜色显示点(xk,yk); } 用牛顿迭代法求f(Z)=Z3-1=0的特解,根据式(1),该方程迭代函数为: 设ρ(Z)=Ze2πi/3,ρ(Z)是绕原点转动120°的旋转变换,则: 根据牛顿迭代法绘制的f(Z)=Z3-1的Julia集如图2所示,可以很明显地观察到图像有关于原点对称的3个部分,3条“链”分别对应f(Z)的3个零点,且每条“链”本身又具有无限精细结构。 图2 牛顿函数φ(Z)=(2Z3+1)/(3Z2)的Julia集Fig.2 Julia set of Newton-Raphson fuction φ(Z)=(2Z3+1)/(3Z2) 图2采用的是图像迭代点色彩与迭代次数相对应的传统着色方案,图像呈现出“链”结构特征。本文将分形图像迭代参数与各种运算符组合构造新型着色方案,图3(a)~(j)所示为其中一种着色方案下,n取不同值时,方程f(Z)=Zn-1=0分别对应的分形图像。 经大量计算机试验后,观察发现:当n=4t时(t为正整数),图像左右两部分各有2t条链,且每条链结构相似;当n=4t-1时,图像左右两部分各有(2t-2)条独立的链,垂直中心线处有两条交融链(由左右两部分链交融形成);当n=4t+1时,图像左右两部分各有2t条完整的链,垂直中心线处有两小段链;当n=4t+2时,图像左右两部分各有2t条链,垂直中心线处有两条完整的链。 由此可知,复多项式f(Z)=Zn-1中n的取值影响图像结构。按照上述规律绘制的分形图像可用于系列化产品包装,实现装潢图形与图形之间的迭代变换和推移组合,这种“自相似”的“重复”结构可强化包装设计的序列视觉变化效果[7]。 图3 不同n值的分形图像Fig.3 Images according to different values of n M=11; C=RGB(255-abs((int)fabs(C1-(2*C2- 255)*pow((log(fabs(l1+l3+ 0.01)))*2,a))%510-255), 255- abs((int)fabs(C2-(3*C3-255)* pow((log(l2*0.1))*4,a)+N)%510- 255), 255-abs((int)fabs(C3- (5*C1-255)*pow((log(fabs(l4+ 0.001)))*3+M,a))%510-255)); 1.1.4 结局指标 ①中央角膜厚度(CCT);②顶端角膜厚度(ACT);③最薄角膜厚度(TCT);④眼压。 break; 由上述代码可知,影响图像着色方案的因素分别为迭代初始参数N和M、颜色初始值(C1,C2,C3)、颜色渐变参数a和颜色通道表达式。现以多项式f(Z)=Z6-1为例,探讨这5个因素对着色效果的影响。 1) 迭代初始参数N不同,其他参数相同。 当颜色初始值RGB为(118,158,108),颜色渐变参数a为5,M为11,颜色通道表达式同图3,N分别为25和26时,对应图像如图4(a)和(b)所示。 2) 迭代初始参数M不同,其他参数相同。 当颜色初值RGB为(118,158,108),颜色渐变参数a为5,N为24,颜色通道表达式同图3,M分别为9和10时,对应图像如图5(a)和(b)所示。 3) 颜色初始值不同,其他参数相同。 当N为24,M为10,颜色渐变参数a为6,颜色通道表达式同图3,颜色初值RGB分别为(118,158,108)和(100,210,140)时,对应分形图像如图6(a)和(b)所示。 图4 不同迭代初始参数N对应的分形图像Fig.4 Images according to different initial iterative parameter N 图5 不同迭代初始参数M对应的分形图像Fig.5 Images according to different initial iterative parameter M 图6 不同颜色初始值对应的分形图像Fig.6 Images according to different initial values of RGB 4) 颜色渐变参数不同,其他参数相同。 当N为24,M为11,颜色初值RGB为(118,158,108),颜色通道表达式同图3,颜色渐变参数a分别为5和6时,对应图像如图7(a)和(b)所示。 5) 颜色通道表达式不同,其他参数相同 当N为25,M为11,颜色初始值RGB为(118,158,108),颜色渐变参数a为6时,颜色通道表达式不同,对应图像分别如图8(a)~(d)所示。 由图4~8可知,对于同一多项式,迭代初始参数、颜色初始值、颜色渐变参数或颜色通道表达式任何一个发生变化都会引起分形图像色彩变化。参数集与运算符的组合形式决定了着色方案,几乎所有的运算符都可使用,如取三角函数、取反三角函数等,并且同一方案中各参数的取值又影响着具体的着色效果。利用上述结论,将分形理论与计算机创作结合,可实现分形图像的数字化和多样化设计[9]。 图7 不同颜色渐变参数a对应的分形图像Fig.7 Images according to different values of color gradient parameter a 图8 不同颜色通道表达式对应的分形图像Fig.8 Images according to different coloring programs 试验证明,牛顿迭代法绘制的复多项式f(Z)=Zn-1的分形图像结构与n的取值有关,且有一定规律可循,借用此规律可设计系列产品包装装潢图案,建立个性化图像素材库;着色方案中参数集或颜色通道表达式的变化均会引起图像色彩变化,开发者可选择不同参数和运算符构造不同着色方案,实现多样化设计,最终将绘制的分形图像用于产品商标或包装以实现防伪。 [1] MANDELBROT B B. The fractal geometry of nature[M].New York: W.H. Freeman and Company,1982. [2]王文,刘夏.广义Julia集在防伪设计中的应用[J].山东建筑大学学报,2013,28(4):386-389. WANG Wen, LIU Xia. Application of Julia set to anti-counterfeiting design[J].Journal of Shandong Jianzhu University, 2013,28(4):386-389. [3]张静,王化雨.基于实数分形的图案设计[J]. 信息技术与信息化,2010,(6):24-26. ZHANG Jing, WANG Huayu. The design of pattern based on real fractal[J]. Information Technology & Informatization, 2010,(6):24-26. [4]叶家鸣,蒋永花.基于牛顿迭代算法的分形艺术图形设计[J].计算机技术与发展,2008,18(4):88-91. YE Jiaming,JIANG Yonghua. Design of fractal art graphics based on Newton iterative algorithm[J]. Computer Technology and Development, 2008,18(4):88-91. [5]田兴彦,邓基园,朱永娇.基于VS的分形图形绘制[J]. 微计算机信息,2012,28(1):1-3. TIAN Xingyan, DENG Jiyuan, ZHU Yongjiao. Use Visual Studio to draw fractal graphic[J]. Microcomputer Information, 2012,28(1):1-3. [6]孙博文.分形算法与程序设计:Visual C++实现[M].北京:科学出版社,2004:118-133. [7]熊承霞.解读当代包装设计中的分形结构创意[J].包装工程,2012,33(18):1-4. XIONG Chengxia. Interpretation of the fractal structure creativity in contemporary packaging design[J].Packaging Engineering, 2012,33(18):1-4. [8]侯思松.牛顿法解方程之混沌情况[EB/OL].( 2014-06-06)[2015-07-20]. http://www.fractal.cn/supply/read.asp?supplyid=134. [9]靳晓晓,陈晨.分形开拓数字化图形设计新思路[J].包装工程,2013,34(22):9-12,23. JIN Xiaoxiao,CHEN Chen.New thinking of digital graphic design of fractal expanding[J]. Packaging Engineering, 2013,34(22):9-12,23. (责任编辑王卫勋,王绪迪) Research on the fractal image of Newton-Raphson method REN Lu, HUANG Yingwei (School of Printing, Packaging Engineering and Digital Media Technology,Xi’an University of Technology, Xi’an 710048,China) The fractal image is mapped through Newton-Raphson method. The graphic parameters and operational rules are used to construct the coloring scheme. The structure characteristics of the fractal image on the complex plane are studied, and a number of new coloring schemes are provided in this paper. The research results indicate that on the complex plane, the structure of fractal images have laws to follow and colors of fractal images are difficult to estimate. Newton-Raphson method; fractal image; structure feature; coloring scheme 1006-4710(2016)02-0247-06 10.19322/j.cnki.issn.1006-4710.2016.02.019 2015-06-02 任露,女,硕士生,研究方向为印刷质量控制与防伪。E-mail :renlu_lenka@163.com 黄颖为,女,教授,研究方向为印刷质量控制与防伪。E-mail :huangyw12@163.com TP391.41 A2 复多项式f(Z)=Zn-1牛顿迭代分形图像结构特征

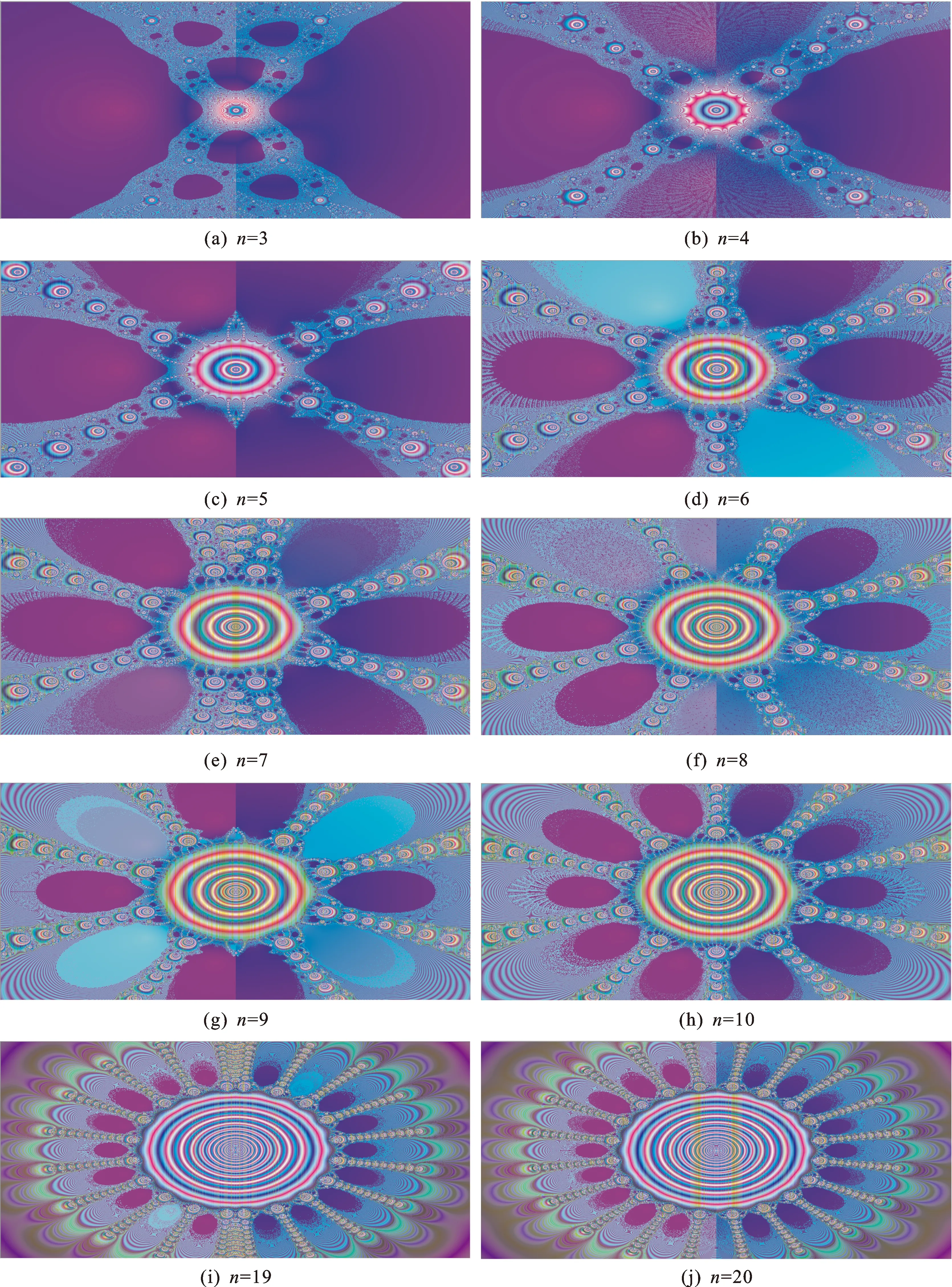
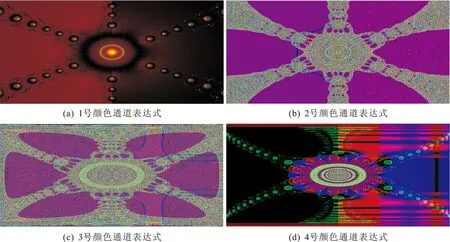
3 复多项式f(Z)=Zn-1牛顿迭代分形图像着色方案
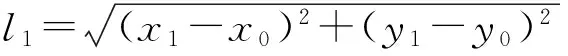
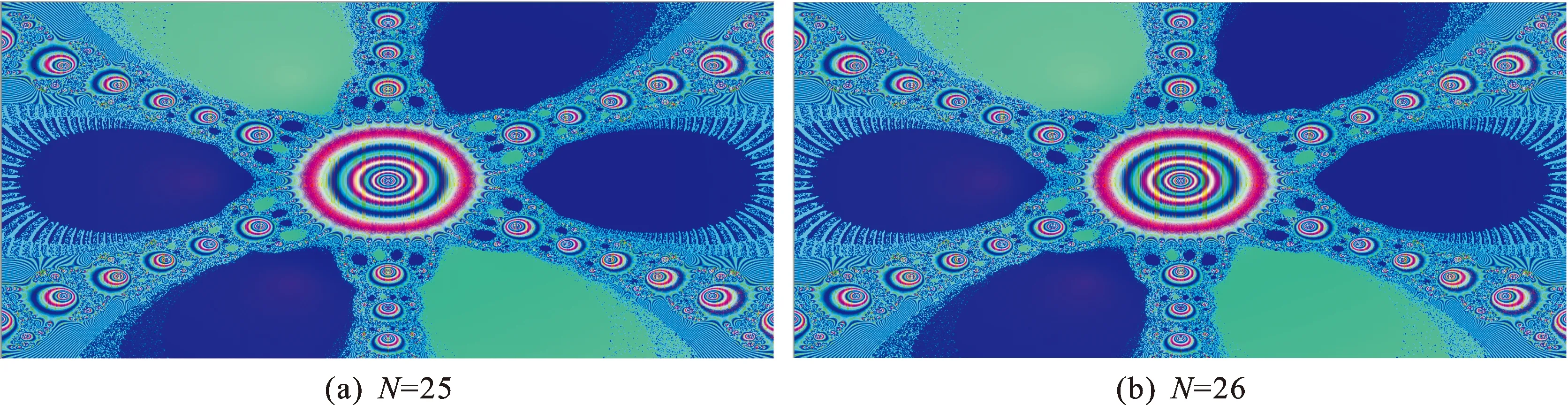


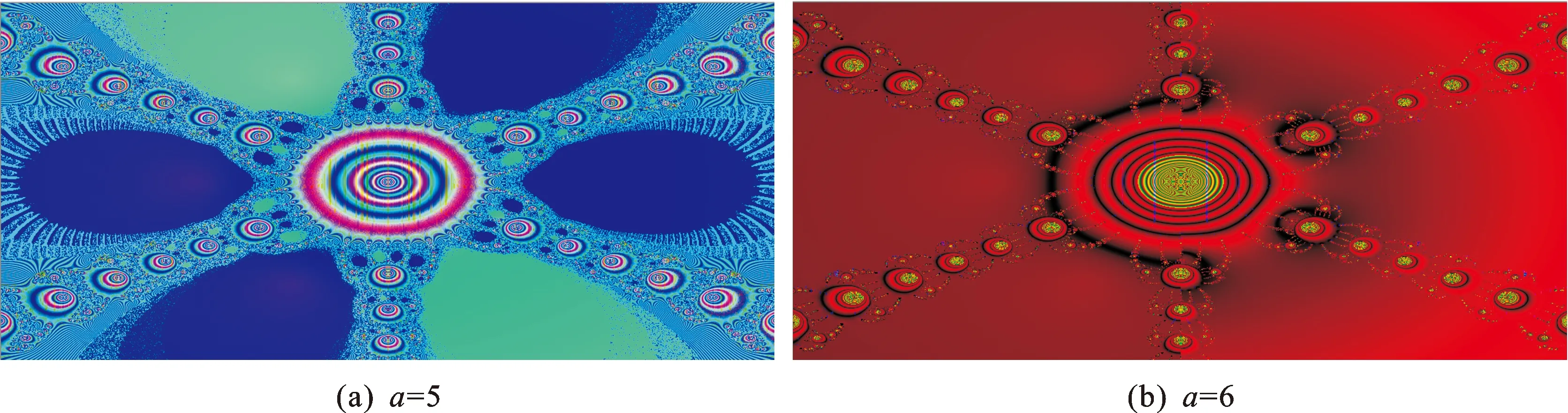
4 结 语

