Comparison of Nonlinear Local Lyapunov Vectors with Bred Vectors, Random Perturbations and Ensemble Transform Kalman Filter Strategies in a Barotropic Model

Jie FENG,Ruiqiang DING,Jianping LI,and Deqiang LIUState Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 00029

2College of Earth Science,University of Chinese Academy of Sciences,Beijing 100049

3Global Systems Division,Earth System Research Laboratory/Oceanic and Atmospheric Research/National Oceanic and Atmospheric Administration,Boulder,CO,80305,USA

4Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology,Chengdu 610225

5College of Global Change and Earth System Sciences,Beijing Normal University,Beijing 100875

6Joint Center for Global Change Studies,Beijing 100875

7Fujian Meteorological Observatory,Fuzhou 350001

Comparison of Nonlinear Local Lyapunov Vectors with Bred Vectors, Random Perturbations and Ensemble Transform Kalman Filter Strategies in a Barotropic Model

Jie FENG1，2，3,Ruiqiang DING1，4,Jianping LI∗5，6,and Deqiang LIU1，2，71
1State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics,Chinese Academy of Sciences,Beijing 100029

2College of Earth Science,University of Chinese Academy of Sciences,Beijing 100049

3Global Systems Division,Earth System Research Laboratory/Oceanic and Atmospheric Research/National Oceanic and Atmospheric Administration,Boulder,CO,80305,USA

4Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology,Chengdu 610225

5College of Global Change and Earth System Sciences,Beijing Normal University,Beijing 100875

6Joint Center for Global Change Studies,Beijing 100875

7Fujian Meteorological Observatory,Fuzhou 350001

(Received 4 January 2016;revised 13 April 2016;accepted 4 May 2016)

The breeding method has been widely used to generate ensemble perturbations in ensemble forecasting due to its simple concept and low computational cost.This method produces the fastest growing perturbation modes to catch the growing components in analysis errors.However,the bred vectors(BVs)are evolved on the same dynamical fl ow,which may increase the dependence of perturbations.In contrast,the nonlinear local Lyapunov vector(NLLV)scheme generates fl ow-dependent perturbations as in the breeding method,but regularly conducts the Gram–Schmidt reorthonormalization processes on the perturbations.The resulting NLLVs span the fast-growing perturbation subspace efficiently,and thus may grasp more components in analysis errors than the BVs.

In thispaper,the NLLVsare employed togenerate initial ensemble perturbations in abarotropic quasi-geostrophic model. The performances of the ensemble forecasts of the NLLV method are systematically compared to those of the random perturbation(RP)technique,and the BV method,as well as its improved version—the ensemble transform Kalman filter(ETKF) method.The results demonstrate that the RP technique has the worst performance in ensemble forecasts,which indicates the importance of a fl ow-dependent initialization scheme.The ensemble perturbation subspaces of the NLLV and ETKF methods are preliminarily shown to catch similar components of analysis errors,which exceed that of the BVs.However,the NLLV scheme demonstrates slightly higher ensemble forecast skill than the ETKF scheme.In addition,the NLLV scheme involves a significantly simpler algorithm and less computation time than the ETKF method,and both demonstrate better ensemble forecast skill than the BV scheme.

ensemble forecasting,bred vector,nonlinear local Lyapunov vector,ensemble transform Kalman filter

1. Introduction

In the past two decades,ensemble forecasting has been substantially developed to become a powerful approach that improves numerical weather prediction(NWP).The basic principle of the generation of initial ensemble members is to sample the uncertainties related to the initial analysis (Epstein,1969;Leith,1974).Various ensemble generation schemes based on dynamical error growth theory have been tested and used in weather prediction centers;for example, the bred vector(BV)method(Toth and Kalnay,1993,1997) used at NCEP,and the singular vector(SV)method(Lorenz, 1965;Molteniet al.,1996)at ECMWF.Afterwards,dataassimilation(DA)schemes were further combined with the dynamical methods to better sample the analysis uncertainties,such as in the ensemble transform Kalman filter(ETKF) scheme(Bishop et al.,2001;Wang and Bishop,2003;Weiet al.,2006,2008)which is an improved version of the BV method,and in the introduction of advanced DA schemes in the SV method(Lawrence et al.,2009).

Numerous studies have been carried out to compare the BV and ETKF approaches(Wang and Bishop,2003;Bowler, 2006;Weiet al.,2006,2008;Descamps and Talagrand, 2007),from which is has been found that the better forecast skill of the ETKF scheme than the breedingscheme is mainly associated with two specific features.One is that the ensemble perturbations of the ETKF scheme can better re fl ect the geographical variations of analysis error variance than those of the breeding scheme.This may be because the BV perturbations are tuned by a time-invariant estimate of analysis error variance(“mask”;Toth and Kalnay,1997),while the ETKF perturbations at each time are updated through the DA algorithm.The other is that the ETKF perturbations are more independent and uncorrelated than the BVs.The BVs arenaturallyevolvedperturbationsthat representthe unstable modes associated with the day-to-day dynamical fl ow.However,dynamical fl ow would drive the BVs to project on the growing type of directions and thus increase the similarity of BVs,especially in local regions.Such similarities are reduced by the nonlinear error growth in NWP models,but can also be seen by the eigenvalue spectrum for BVs(Wang and Bishop,2003;Bowler,2006).In contrast,the ETKF ensemble perturbations are orthogonal in observation space(Wang and Bishop,2003;Weiet al.,2006).

In view of the interdependence among BVs,Feng et al. (2014)developed the nonlinear local Lyapunov vectors(NLLVs),which are the nonlinear extension of the linear Lyapunovvectors(LVs).The traditional LVs de fine a set of timedependent orthogonal perturbation structures(Kalnay,2002; Trevisan and Palatella,2011).These perturbations point to the directions with diff erent growth rates in phase space specified by positive,null and negative Lyapunov exponents (Benettin et al.,1980;Wolf et al.,1985;Fraedrich,1987; Trevisan and Legnani,1995;Vannitsem and Nicolis,1997). Therefore,the LVs can be used to identify the unstable,neutral and stable subspaces.In reality,on the one hand,the unstable perturbation subspace has a significantly smaller dimension than the stable subspace,and thus is much easier to besampled(TothandKalnay,1997);whileontheotherhand, any perturbation,through model integration,will eliminate the non-growing components in it,and project onto the fastgrowing subspace with relatively small dimension.Therefore,the identification of unstable perturbations is critical to the improvementof NWP(Zhang et al.,2015),like the accurate estimation of error variances in the backgroundforecasts of DA(Trevisan and Uboldi,2004;Carrassiet al.,2007), and the generation of ensemble perturbations in ensemble forecasting(Toth and Kalnay,1997),etc.This is also why the LVs are gradually developed and applied in DA,ensemble generation and other areas in numerical forecasting.The NLLVs bear some similarities to the LVs;for example,they are orthogonal to each other and have diff erent error growth rates from the largest to the smallest.However,they also have significant diff erences.The LVs are generated through a long-term integration using the tangent linear model and the direction of the leading LV is independent of the initial perturbation(Kalnay,2002).In comparison,the NLLVs are obtained by integrating the nonlinear model from both the perturbed and unperturbed initial conditions,and represent diff erent types of instabilities with diff erent rescaling amplitudes of perturbations.

Both the BVs and the NLLVs are nonlinear extensions of LLVs,and can be dynamically produced by a sequence of two nonlinear model integrations with a periodic rescaling of their diff erence.BVs are random samples in the small fastest growing space,and have consistently large projection on the leading LLV(Magnusson et al.,2008).However,NWP models usually have a multidimensional growing subspace.Various independent fast growing directions should be comprehensively considered to span the unstable subspace(Duan and Huo,2016).The fastest growing directions captured by the BVs have limited diversity and may not contain sufficient information to represent the development of analysis errors.In contrast,apart from the leading NLLV(LNLLV)being similar to the BVs,which tend to the fastest growing direction,other successively orthogonalized NLLVs point to additional fast growing directions in phase space.The NLLVs have larger diversity than the BVs and may capturea largeramountof componentsin analysis errors (Feng et al.,2014).

The NLLV method is related to the ETKF method,both of which are designed to orthogonalize perturbations.In the ETKF approach,the ensemble perturbation matrix is transformed by the matrix TTT associated with the covariance matrixofforecastmembersandobservations(WangandBishop, 2003).In comparison,the NLLVs are orthogonalized using the Gram–Schmidt reorthonormalization(GSR)technique. Given that the ETKF scheme has been successfully implemented in operational forecast centers,it is worthwhile comparing the NLLV approach with the ETKF approach.The results of the BV and the random perturbation(RP)approaches are also given as reference,and all the comparisons are presented in a barotropic model.To clarify the diff erences between these four initialization methods,the experiments are implemented in a perfect model environment,and by using the same analysis and the same forecast model.An assimilation scheme independent of each ensemble initialization scheme—namely,the ensemble Kalman filter(EnKF; Houtekamer and Mitchell,1998;Evensen,2003,2004)—is used to produce the initial analysis states.

This paper is organized as follows:Section 2 describes the BV,ETKF and NLLV ensemble generation schemes.An introduction to the barotropic model and the basic setup of the numerical experiments is provided in section 3.Section 4 presents the results of the quantitative comparison of the four ensemble methods.Section 5 provides a discussion and conclusions.

2. Initial perturbation schemes

2.1. BV scheme

The breeding method proposed by Toth and Kalnay (1993,1997)is used to simulate the error evolution in each analysis cycle.RPs are superposed on the analysis state to grow as a perturbation between two model integrations.At the end of each breeding cycle(12 hours in our experiments), the perturbations are rescaled by an appropriate factor.This, w ithout the insertion of further random noise,de fines a new set of perturbations that are used to generate the next perturbed initial states.This process is repeated and,as the effect of the particular initial RP dim inishes,the resulting perturbationsbecome the BVs.Initially,Toth and Kalnay(1993) used a global rescaling factor that is close to the empirically estimated global analysis RMSE.However,to ensure that the ensembleperturbationmagnitude re fl ects the regionally varying uncertainties in the analysis,the breeding method used at NCEP includes an estimated mask as a constraint of BVs (Toth and Kalnay,1997).Ow ing to our experiments having observationsoneverygrid over thewhole fieldandhaving the same precision,the distribution of analysis error variances is mainly determ ined by the forecasterrorvariances.Therefore, only a simple global rescaling factor is applied in this study. The BVs are calculated using a Euclidean norm.Through a five-day breeding process,the generated BVs are tuned to the amplitude of the global analysis RMSE to use as the initial ensemble perturbations.

2.2. ETKF scheme

The ETKF perturbations are generated based on an en-perposed on the control analysis.Forecast perturbations are listed as columns in the matrixand analysis perturbations are listed as columns in the matrixThe scheme is created to calculate a transformationmatrix,TTT,which transforms the forecast perturbations according to

In this expression,TTTis anN×Nmatrix,and can becalculated as

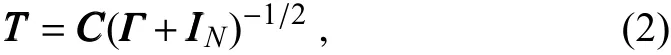
where columns of the matrixCCCcontain the eigenvectors ofthe corresponding eigenvalues.HHHdenotes the mapping from themodelspace to theobservation space.RRRis theobservation error covariance matrix.The ETKF ensemble perturbations can be proved orthogonal to each other in the space of the observations(Wang and Bishop,2003).

The forecast perturbationsin each cycle are multiplied by an in fl ation factor of 7%to maintain su fficient spread.The updated ensemble perturbations w ill be added to the control analysis to generate the initial conditions for the next filter step.The length of a cycle is 12 hours and the process is continued over 5 days to the initial analysis for forecasting.Each model grid has the same observation error variance of 0.02, i.e.the observation error covariance matrixRRRis a diagonal matrix w ith 0.02 entries.

2.3. NLLV scheme

Let us consider ann-dimensional nonlinear dynam ical system:

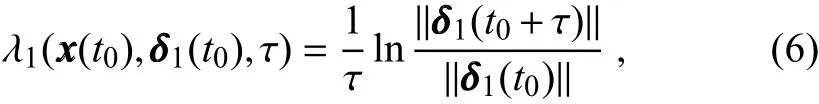
While the LNLLV tends to the fastest grow ing direction, the rest of the NLLVs can be derived via a periodic reorthogonalization by the GSR process(Wolf et al.,1985;Liand Wang,2008,Feng et al.,2014).The orthogonalized perturbations are then globally rescaled to the initial size and again superposed on the new analysis to integrate(see Fig.1).The process is performed for five days w ith a 12-hour cycle to acquire the NLLVs denoted byThis 5-day period is basically close to that used in Vannitsem and Nicolis(1997)to generate LVs in a quasigeostrophic model. The NLLVs are orthogonal to each other,representing thevectors along the directions from the fastest growing direction to the fastest shrinking direction in local phase space. The resulting NLLV perturbations are tuned to the amplitude of the global analysis RMSE and superposed on the analysis to generate ensemble members.

Fig.1.Creation of NLLVs.A group of RPs is initially introduced on the analysis state,and integrated to the end of a breeding cycle.The orthogonalization processes are conducted regularly.The red solid curve represents the leading perturbed forecast during each cycle,and the black solid curves represent other perturbed forecasts from the second to the nth fastest.The direction of the fastest growing mode(LNLLV,red dashed line)is kept,and the other directions (black dashed lines)are orthogonalized successively to acquire NLLV2to NLLVn(blue dashed line).These perturbations are then rescaled to the same size as the initial perturbations,and added to the new analysis.After several days of cycling,the perturbations are dominated by growing components[modified from Feng et al.(2014)].

Once the NLLVs are obtained,the growth rate of perturbations along each direction can be estimated by the NLLEs, which are de fined by

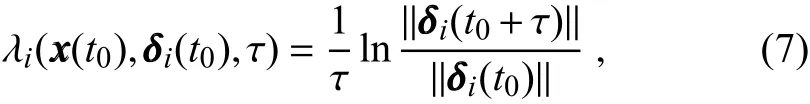
Thebackgroundforecasterrorsinsertedintheanalysiserrors are the combined e ff ects of the multidimensional growing subspace(Palatella and Trevisan,2015)spanningthe NLLVs.Therefore,to better sample the analysis errors,the initial ensemble perturbations are constructed by a simple random linear combination of the first N NLLVs(N=10).The NLLVs are denoted bythen the orthogonal ensemble perturbations Δ can be calculated by

whereβis an N×N matrix.The column vectors ofβare constructed by random numbers of a standard normal distribution and are independent from each other.The resulting ensemble perturbations are rescaled to the amplitude of the global analysis error and superposed on the analysis to generate ensemble members.

3. Experimental setup

The two-dimensional quasi-geostrophic model is governed by the following system of dimensionless diff erential equations:

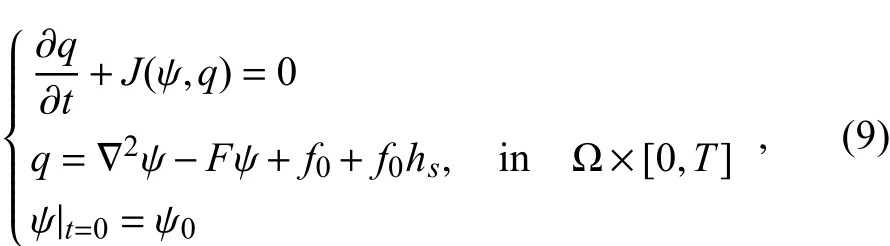
where the variables q and ψ are the potential vorticity and the stream function,respectively;andare the Laplacian operator and the horizontal Jacobian operator,respectively;k and l represent the zonal and meridional coordinates;and t denotes time.The planetaryFroudenumberF=0.102,andtheCoriolisparameter f0=10.0.A double periodical boundaryconditionis used for Ω=[0，K]×[0，L].The barotropic model has been used in various studies of predictability and ensemble forecasts (Barkmeijer,1992;Cheung and Chan,1999;Mu and Zhang, 2006;Mu and Jiang,2008;Durran and Gingrich,2014).

All the experiments below are performed on a 32×16 latitude–longitude horizontal grid.The grid spacing d= 0.2 corresponds to a dimensional length of 200 km,and the time step dt=0.006 corresponds to 10 min.The basic fl ow is obtained by integrating(10)with an initial state=0.5sin(πk/6.4)+sin(πl/3.2)+0.5,as used by Mu and Jiang(2008).For simplicity,the topography is only a func-tion of the l-direction hs=h0×[sin(2πl/3.2)+1].

The quasi-geostrophic model is integrated for 800 days as a“truth run”,after a first“spin-up”run of 100 days. The quality of the forecasts are assessed by comparing with the truth run.For a fair comparison,the EnKF assimilation method,which is irrelevant to the ensemble generation schemes,is used to generate the control analysis.The observationsare distributedat each gridpoint,andare producedby addinga randomnoise to the true state.The assimilation process is implemented every 12 hours on the stream function. The details of the EnKF assimilation steps are described in Appendix A.

Once the analysis states have been obtained,10-day ensemble forecasts initialized from the four ensemble generation methods,respectively,are implemented.All the initial ensemble perturbations are produced using the Euclidean norm.The RP perturbations are simply generated by random numbers with a standard normal distribution,and then rescaled to the amplitude of initial analysis errors.The ensemble perturbations of the RP scheme are fl ow-independent and thus can provide a proper reference for the other theorybased schemes(Magnusson et al.,2009).To clarify the differences of the four initialization schemes in a simple way, in this study,the N=10 ensemble perturbations for the four schemesaredirectlysuperposedontheanalysisstate,without being centered,to generate ensemble members.The statistical quality of the forecasts is assessed by averaging a set of 100 diff erent experiments,each corresponding to a diff erent initial state randomly chosen from the 800-day truth run.All experimentsare“perfectmodel”experimentsinwhichtheassimilation and forecasts are performed with the same model used for producing the truth run.

4. Results

4.1. NLLEs of the barotropic model

Before using the barotropicmodel to computethe NLLEs and NLLVs,it should be ensured that this model is a nonlinear dynamical system and has a chaotic attractor(Liand Chou,1997).Figure 2 shows the temporal evolution of the stream function at one grid point for 800 days.It can be seen that the trajectory presents a chaotic behavior,which indicates the model is suitable for the research on nonlinear error growth.

To see if diff erent growing directions can be e ff ectively captured by the NLLVs,the transient error growths of NLLVs are measured by the NLLEs.Figure 3 shows the first 50 NLLEs averaged over 800 initial conditions with a oneday interval.The NLLEs are calculated for the error growth during the initial τ=12 h and the initial amplitude of perturbations is 0.01.It can be seen that the first 50 NLLEs are consistently positive and continuously arranged in a decreasing order.The results demonstrate that the barotropic model has a high-dimensional growing subspace.The development of the analysis error is a combined e ff ect of various independent growing directions,and the NLLVs may be capable of capturing the unstable subspace e ff ectively.

4.2. Independence of perturbations

Since analysis errors are poorly known,the initial ensemble perturbations should be as independent as possible to samplethe possibledirectionofanalysis errors.To see the independenceof the globalperturbations,the averagevariances explainedbytheeigenvectorsoftheensemblecovariancematrix are calculated for the four schemes,respectively(Wang and Bishop,2003;Bowler,2006).The assessments for the ensemble perturbations superposed on the control forecasts at the diff erent lead times are shown in Fig.4.A fl atter distribution of the explained variance indicates better perturbation independence.At day 0,the explained variances for the NLLVandETKF perturbationsarestrictly evenlydistributed, which can be induced by their theoretical concepts.The RP perturbationsareveryclose tobeingorthogonaltoeach other. However,the first eigenvector of the BVs explains almost 30%of the error variance when 10 perturbations are used, indicating that there is certain similarity among the perturbations.That is to say,the e ff ective number of ensemble perturbations for the BV method is lower than its actual number.With the increase in lead time,the similarities among the ensemble perturbations for the four schemes gradually increase due to the dynamical evolution on the same basic fl ows.The performances of the four initialization schemes tend to be similar after about day 6.

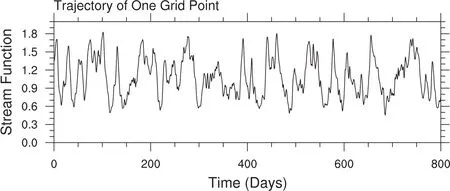
Fig.2.The evolution of the stream function at one grid point of the barotropic model for 800 days.

Fig.3.The first 50 NLLEs for the barotropic model with the evolution time τ equal to 12 hours and a finite initial amplitude of 0.01.

Initial ensemble perturbations are created to sample the possible forecast errors.Therefore,the variance of forecast errors explainedby the subspaceof ensemble perturbationsis an important assessment of the quality of perturbations.For a fair comparison of the four schemes,the ensemble forecast errors are de fined as the diff erence between each ensemble forecast member and the control forecast,while the control forecast error is the diff erence between the true state and the control forecast.Let us assume the normalized ensemble forecast errors are denoted by EE = ee1， ee2，...， eeN,and the control forecast error is ee0.The projection of the control forecast error on the subspace of ensemble forecast errors would be derived byThen,the error variance of the controlforecastexplainedbytheensembleperturbationsubspace can be calculated through the correlation between pp and ee0.

Figure 5 illustrates the variance of analysis errors explainedbytheensembleperturbationssuperposedonthecontrol forecasts as a function of lead time for the four methods. At the initial time,the RP approach performs the worst in terms of capturing the analysis error direction,as the RPs are independent of the fl ow at initial time.The NLLV and ETKF perturbationshave similar explainedvariance,whichis larger than that of the BV perturbations.This may be due to the moreindependentperturbationsoftheformertwoapproaches than thelatterone(seeFig.4).Theinitialexplainedvariances ofthefourschemesmay also causetheirrelativeperformance afterwards.The ETKF and NLLV techniques basically remain similar and the best from day 0 to 10.The BV approach always has a lower score compared to the ETKF and NLLV approaches during the 10 days.The explained variance for the RP,despite exhibiting the fastest increase among the four schemes,has the worst performance throughout.

Fig.4.Mean explained variances of the eigenvectors of forecast covariance matrices measured from day 0 to 10.The BV,NLLV,RP and ETKF methods are denoted by triangles,open circles,squares and crosses,respectively.

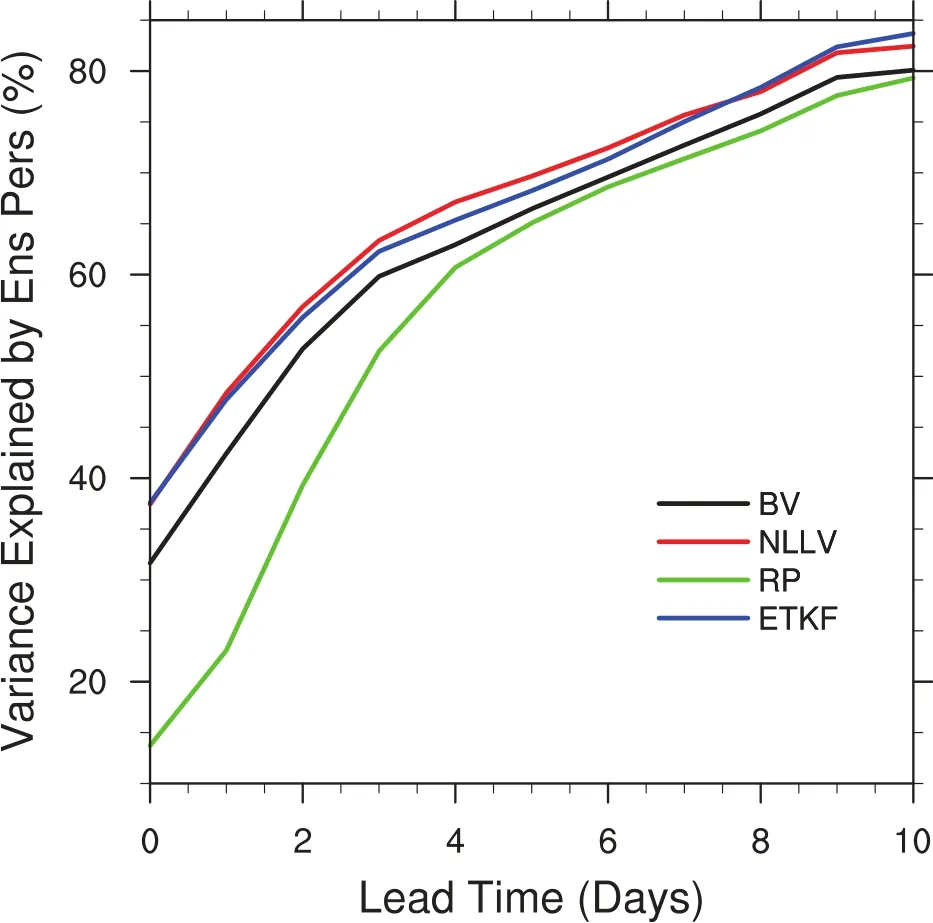
Fig.5.Evolution of mean error variance of the control run explainedbytheensemble perturbations asafunctionof leadtime.

4.3. Skill of the ensemble mean

The RMSE and the pattern anomaly correlation(PAC) of the ensemble mean are often used to measure the overall forecast performance of ensemble forecasts.Figure 6 illustrates the RMSE and PAC as a function of time for the four schemes.The ensemble spread,calculated as the standard deviation of ensemble members,is also given as a reference. The ensemble spread of a statistically reliable ensemble system is usually close to the RMSE of the ensemble mean for all lead times(Buizza et al.,2005).From Fig.6a,it can be seen that for the first 4 days the NLLV,RP and ETKF ensembles have similar RMSE scores,which are slightly smaller than that of the BV scheme.This may because the BVs are constrained to a smaller perturbation subspace compared to the other three types of initial perturbations(see Fig.4).Note that the ensemble spread of the RP approach is smaller than the other three for 0–4 days.This is due to the RPs pointing to non-growing directions and will shrink initially(Toth and Kalnay,1997).From day 4 to 10,the NLLV has slightly smaller RMSE and similar ensemble spread compared with ETKF,while the BV scheme has somewhat larger RMSE and smaller spread than both the NLLV and ETKF schemes. This is because the NLLV perturbations,which consider the nonlinear interactions of growing directions,have a better sampling of the development of the analysis errors than the ETKF perturbations,and both of them span more orthogonal and uncorrelated subspaces than do the BVs.Although the RP approach has the largest ensemble spread,its forecast skill decreasesrapidlyand remainsthe lowest amongthe four schemes.This can be explained by the RPs having very limited ability to capture the evolution of initial analysis errors. The ensemble spread for both the NLLV and ETKF methods are closer to their respective ensemble mean errors than the BV method,which implies that the former two have better statistical reliability than the latter one.The PAC score in Fig.6b presentssimilar relative performanceof the ensemble mean skill as the RMSE.

Figure 7 shows the ratio of the highest ensemble mean skill among the four initialization schemes for each of them as a function of lead time.It can be seen that the ETKF and NLLV approaches basically have similar ratios to reach the highest forecast skill,which is evidently higher than that of the BV andRP approaches.TheRP approachperformsbetterthan the BV approachfromday 1 to 4.Thereafter,the ratioof the RP scheme remains the lowest amongthe fourschemes to the end of the lead time.The statistical results for each case basically correspond to the sample mean results.

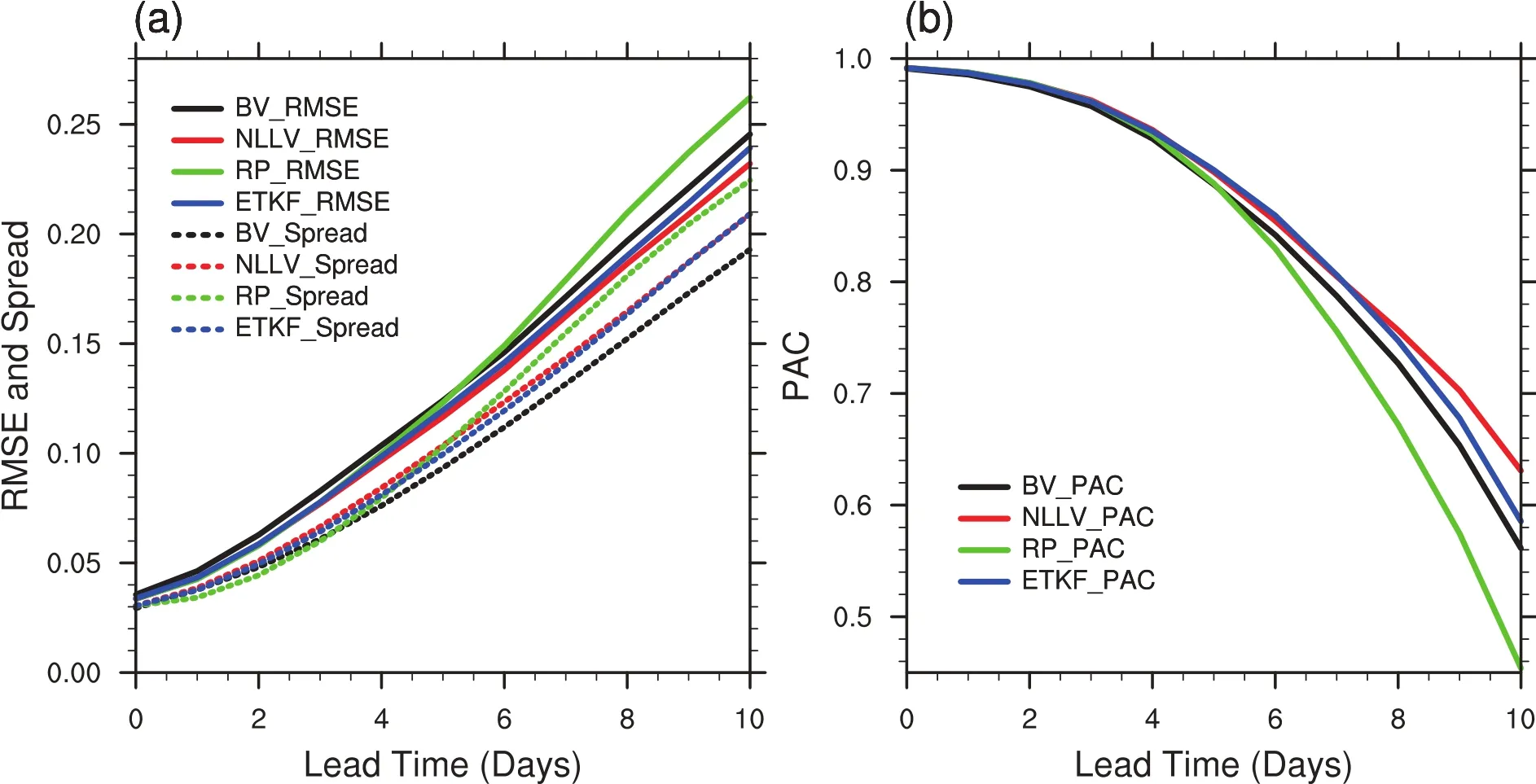
Fig.6.Evolution of the(a)mean RMSE(solid lines)and ensemble spread(dashed lines)and(b)PAC(solid lines)for the BV, NLLV,RP and ETKF schemes as a function of lead time.

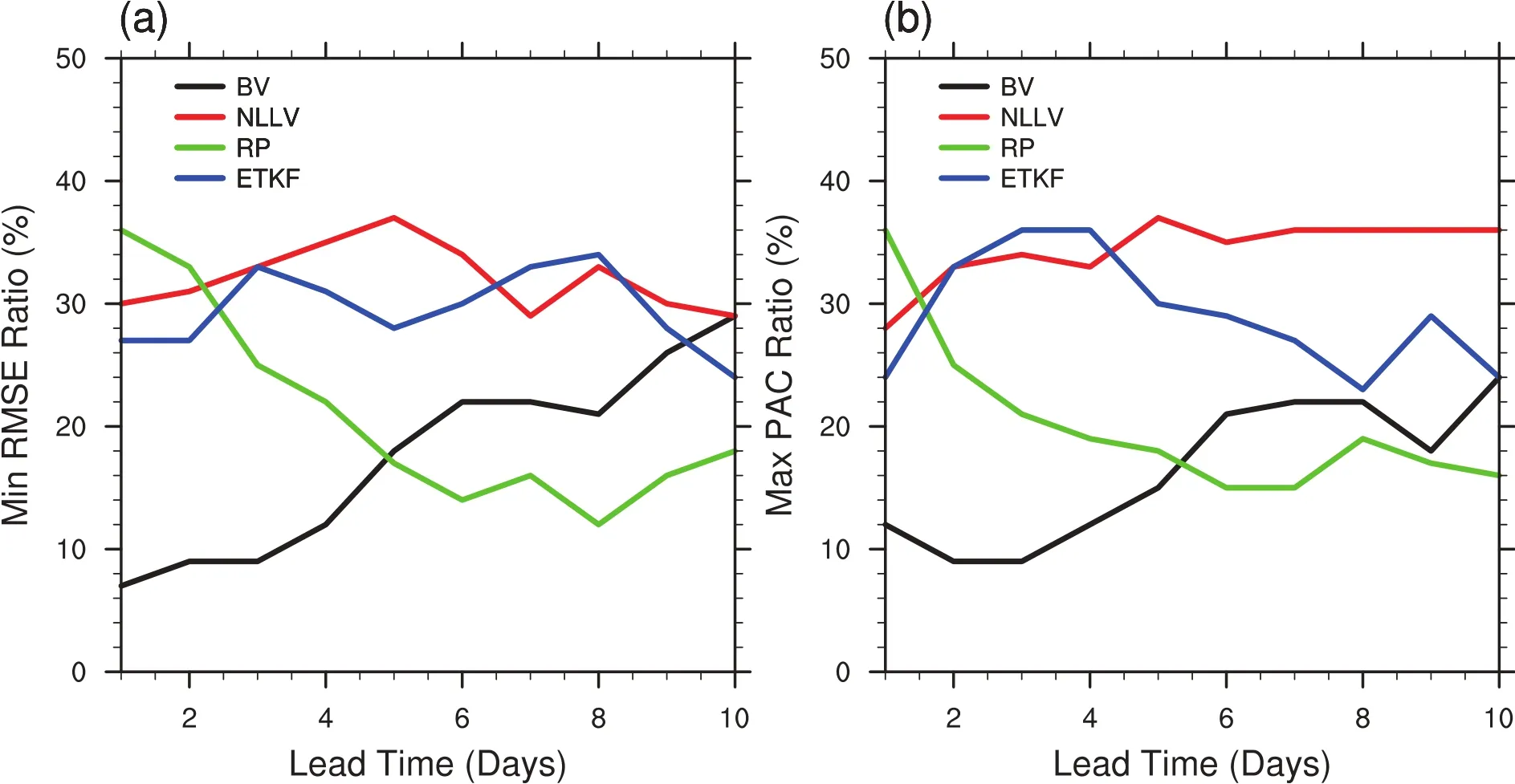
Fig.7.Evolution of the ratio of the(a)smallest RMSE and(b)highest PAC among the BV,NLLV,RP and ETKF initialization schemes for each of them as a function of lead time.

4.4. Brier skill score

A commonly used measure in probabilistic forecasts is the Brier score(BS),which can be used to evaluate the reliability(BSrel)and resolution(BSres)of an ensemble forecast system(Murphy,1973;Descamps and Talagrand,2007; Stephenson et al.,2008).The score assesses the performance of the probability forecast of the occurrence of an event Φ. Further details are given in,for example,Descamps and Talagrand(2007)and Stephenson et al.(2008).In this paper, Φ is de fined as the eventψ＞ψc,whereψcis the climatological mean at each grid point.A smaller value of BS and BSrelindicates a better forecast skill;while the BSresacts in an opposite way.Another event interval(ψ＞ψc+σ,where σ is the standard deviation ofψ)is also introduced for diagnostics,but does not appear to a ff ect the relative performance of the ensemble forecasts.Only the results of the event Φ are shown in this paper.

Figure 8a shows the basic BS evaluatedfor the fourmethods as a function of lead time.The four methods have similar basic BS scores during days 0–4.The NLLV scheme shows slightly better performance than the ETKF scheme.The BV scheme has a lower basic BS than the RP scheme for days 4–10,and both of them perform worse than the ETKF and NLLV schemes.Their diff erences in BS performance mainly come from the BSresand the BSrelcomponents,as shown in Fig.8b.After 4 days,the higher BSresof the NLLV and the ETKF schemes than the BV scheme may be attributable to the worse sampling of the analysis errors by the BV approach.Meanwhile,the former two approaches have better independence and larger ensemble spread than the BV approach,which may result in a lower BSrelrelative to the BV approach.The RP scheme performs worst among the four schemes generally.This is because the RP ensemble is randomly generated,and thus is less likely to describe the probability distribution of the truth relative to the other three schemes.

5. Discussion and conclusions

The NLLV ensemble generation scheme retains the advantage of the BV scheme,which uses the breeding cycles to capture the development of analysis errors in the assimilation cycles and is very simple and cheap to implement. Diff erent from the BVs,the NLLV perturbations are periodically orthogonalized by the GSR process to identify various distinguished growing perturbations,and thus have more diversity and independence.In this paper,the application of the NLLV method introduced by Feng et al.(2014)for the generation of ensemble perturbations is further extended to a moderately complex barotropic model.Except for the BV and RP approaches,the performance of the NLLV scheme for ensemble forecasting is further compared with that of the ETKF scheme,which is one of the most advanced ensemble initialization schemes.It is found that the NLLV scheme performs slightly better overall than the ETKF scheme for various scores when the observationsto be assimilated are evenly distributed at each grid.This may because the development of analysis errors can be e ff ectively sampled by the unstable perturbations acquired by the NLLVs.The BV approach performs worse than the ETKF and NLLV approaches dueto the dependenceamongperturbations,but still dramatically exceeds the RP approach.

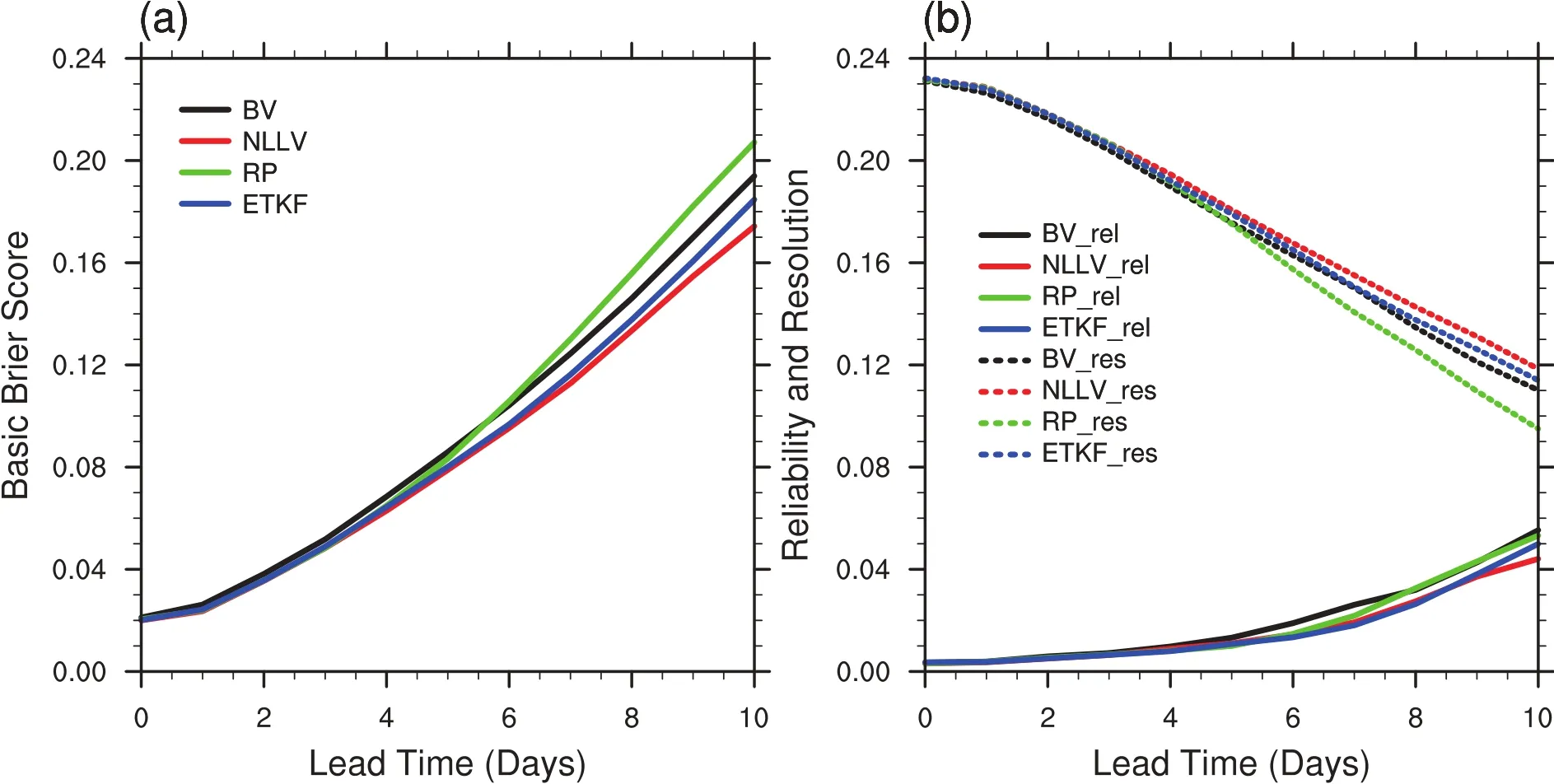
Fig.8.Evolution of(a)average basic BS asa function of lead timefor the BV,NLLV,RP and ETKF schemes;and(b)resolution (dotted lines)and reliability(solid lines)contributions to the BS.

This study simply uses a barotropicmodel without model error,and the model size is less than that of operational forecasts.However,the quasi-geostrophic model is sufficiently large to demonstrate the relative performance of the ensemble schemes accurately.Despite the similar forecast skills of the NLLV and ETKF schemes,the generation of the NLLVs is significantly time-saving and easy to implement,compared to the ETKF scheme.The computational expense of the former is only about one third of the latter in the experimental environment of this paper.Meanwhile,the quality of ETKF perturbations largely depends on the estimation of the background and observation covariance matrices,while an accurate estimate of theforecast errorcovarianceis verychallenging due to such problems as ensemble“collapse”(Anderson and Anderson,1999)and spurious correlations at large distances(Houtekamer and Mitchell,2001).In a real world situation where the observations are irregularly distributed, a prior knowledge of the regional rescaling factors could be used to modulate the NLLV perturbations to better sample the analysis error variances.Several current approaches can provide the estimated masks,like the error growth statistical method(Pe˜na and Toth,2014).Introducing the estimation of analysis error variances in tuning the NLLV perturbations may further improvethe ensemble forecast skill of the NLLV scheme.

Acknowledgements.Wewould like tothank Dr.Zhina JIANG for providing the Barotropic Quasi-geostrophic Model and Dr.SiSHEN for discussions on EnKF DA.This research was jointly supported by NSFC projects(Grant Nos.41375110 and 41175069) and the 973 projects of China(Grant Nos.2012CB955200 and 2010CB950400).

Appendix A

The Ensemble Kalman Filter

The true state is denoted by xxxtrue,which is derived from a long-term model integration.The simulated observations yyy are generated based on the true state using

whereHHprovides a mapping from the model space to the observation space,and ε represents independent realizations of the noise with a Gaussian distribution N(0，0.02).The ensembleofforecaststates isadoptedasbackgroundstates.The ensemble matrix is then de fined as

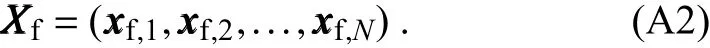
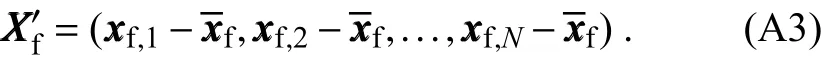
The covariance matrix of the ensemble XXXfis:

The background forecast ensemble is to be updated by the observations.The set yyyi(i=1，2，...，N)is a set of perturbed observations that are associated with each previous forecast of the ensemble.They are de fined as:

The RPs εifollow the same distribution as ε.The observations are assimilated to produce a new analysis of the state:

The Kalman gainKis calculated by:

This is actually a weight measuring the ratio of the forecast and observational error covariance.RRis the observational error covariance matrix.

To overcome the problem of undersampling,a 7%variance in fl ation factor is applied toin this barotropicmodel. Moreover,the number of the ensemble is 100,which is much smaller than the model dimension.Therefore,the localization technique is applied to the matrixPPfto prevent spurious correlations at large distances.This is realized by the fifthorder function of Gaspariand Cohn(1999)with a distance of zero correlation equal to 800 km(four grids).The assimilation cycles are repeated for 30 days in each case to generate the analysis ensemble.The meanof the analyzed ensembleis regarded as the initial analysis state when performing the forecasts.

REFERENCES

Anderson,J.L.,andS.Anderson,1999:AMonte Carloimplementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts.Mon.Wea.Rev.,127,2741–2758.

Barkmeijer,J.,1992:Local error growth in a barotropic model.Tellus A,44,314–323.

Benettin,G.,L.Galgani,A.Giorgilli,and J.M.Strelcyn,1980: Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems;a method for computing all of them.Part 1:Theory.Meccanica,15,9–20.

Bishop,C.H.,B.J.Etherton,and S.J.Majumdar,2001:Adaptive sampling with the ensemble transform Kalman filter.Part I: theoretical aspects.Mon.Wea.Rev.,129,420–436.

Bowler,N.E.,2006:Comparison of error breeding,singular vectors,random perturbations and ensemble Kalman filter perturbation strategies on a simple model.Tellus A,58,538–548.

Buizza,R.,P.L.Houtekamer,Z.Toth,G.Pellerin,M.Z,Wei,and Y.J.Zhu,2005:A comparison of the ECMWF,MSC,and NCEP global ensemble prediction systems.Mon.Wea.Rev.,133,1076–1097.

Carrassi,A.,A.Trevisan,and F.Uboldi,2007:Adaptive observations and assimilation in the unstable subspace by breeding on the data assimilation system.Tellus A,59(1),101–113.

Cheung,K.K.W.,and J.C.L.Chan,1999:Ensemble forecasting of tropical cyclone motion using a barotropic model.Part I: perturbations of the environment.Mon.Wea.Rev.,127,1229–1243.

Descamps,L.,and O.Talagrand,2007:On some aspects of the de finition of initial conditions for ensemble prediction.Mon.Wea.Rev.,135,3260–3272.

Ding,R.Q.,and J.P.Li,2007:Nonlinear finite-time Lyapunov exponent and predictability.Physics Letters A,364,396–400.

Ding,R.Q.,J.P.Li,and K.-J.Ha,2008:Trends and interdecadal changes of weather predictability during 1950s-1990s.J. Geophys.Res.,113,D24112,doi:10.1029/2008JD010404.

Ding,R.Q.,J.P.Li,and K.-H.Seo,2010:Predictability of the Madden-Julian oscillation estimated using observational data.Mon.Wea.Rev.,138,1004–1013.

Ding,R.Q.,J.P.Li,and K.-H.Seo,2011:Estimate of the predictability of boreal summer and winter intraseasonal oscillations from observations.Mon.Wea.Rev.,139,2421–2438.

Duan,W.S.,and Z.H.Huo,2016:An approach to generating mutually independent initial perturbations for ensemble forecasts:orthogonal conditional nonlinear optimal perturbations.J.Atmos.Sci.,73,997–1014,doi:10.1175/JAS-D-15-0138.1.

Durran,D.R.,and M.Gingrich,2014:Atmospheric predictability: Why butter fl iesare not of practical importance.J.Atmos.Sci.,71,2476–2488.

Epstein,E.S.,1969:Stochastic dynamic prediction.Tellus,21, 739–759.

Evensen,G.,2003:The ensemble Kalman filter:theoretical formulation and practical implementation.Ocean Dynamics,53, 343–367.

Evensen,G.,2004:Sampling strategies and square root analysis schemes for the EnKF.Ocean Dynamics,54,539–560.

Feng,J.,R.Q.Ding,D.Q.Liu,and J.P.Li,2014:The application of nonlinear local Lyapunov vectors to ensemble predictions in the Lorenz systems.J.Atmos.Sci.,71(9),3554–3567.

Fraedrich,K.,1987:Estimating weather and climate predictability on attractors.J.Atmos.Sci.,44,722–728.

Gaspari,G.,and S.E.Cohn,1999:Construction of correlation functions in two and three dimensions.Quart.J.Roy.Meteor.Soc.,125,723–757.

Houtekamer,P.L.,and H.L.Mitchell,1998:Data assimilation using an ensemble Kalman filter technique.Mon.Wea.Rev.,126,796–811.

Houtekamer,P.L.,and H.L.Mitchell,2001:A sequential ensemble Kalman filter for atmospheric data assimilation.Mon.Wea.Rev.,129,123–137.

Kalnay,E.,2002:Atmospheric Modeling,Data Assimilation and Predictability.Cambridge University Press,221 pp.

Lawrence,A.R.,M.Leutbecher,and T.N.Palmer,2009:The characteristics of Hessian singular vectors using an advanced data assimilation scheme.Quart.J.Roy.Meteor.Soc.,135, 1117–1132.

Leith,C.E.,1974:Theoretical skill of Monte Carlo forecasts.Mon.Wea.Rev.,102,409–418.

Li,J.P.,and J.F.Chou,1997:Existence of the atmosphere attractor.Science in China Series D:Earth Sciences,40(2),215–220.

Li,J.P.,and S.H.Wang,2008:Some mathematical and numerical issues in geophysical fl uid dynamics and climate dynamics.Communications in Computational Physics,3,759–793.

Li,J.P.,and R.Q.Ding,2011:Temporal-spatial distribution of atmospheric predictability limit by local dynamical analogs.Mon.Wea.Rev.,139,3265–3283.

Li,J.P.,and R.Q.Ding,2013:Temporal-spatial distribution of the predictability limit of monthly sea surface temperature in the global oceans.Int.J.Climatol.,33,1936–1947.

Li,J.P.,R.Q.Ding,and B.H.Chen,2006:Review and Prospect on the Predictability Study of the Atmosphere.Review and Prospects of the Developments of Atmosphere Sciences in Early 21st Century.China Meteorology Press,96–104.(in Chinese)

Lorenz,E.N.,1965:A study of the predictability of a 28-variable atmospheric model.Tellus,17,321–333.

Magnusson,L.,E.K¨all´en,and J.Nycander,2008:Initial state perturbations in ensemble forecasting.Nonlinear Processes in Geophysics,15,751–759.

Magnusson,L.,J.Nycander,and E.K¨all´en,2009:Flow-dependent versus fl ow-independent initial perturbations for ensemble prediction.Tellus A,61(2),194–209.

Molteni,F.,R.Buizza,T.N.Palmer,and T.Petroliagis,1996:The new ECMWF ensemble prediction system:methodology and validation.Quart.J.Roy.Meteor.Soc.,122,73–119.

Mu,M.,and Z.Y.Zhang,2006:Conditional nonlinear optimal perturbations of a two-dimensional quasigeostrophic model.J.Atmos.Sci.,63,1587–1604.

Mu,M.,and Z.N.Jiang,2008:A new approach to the generation of initial perturbations for ensemble prediction:Conditional nonlinear optimal perturbation.Chinese Science Bulletin,53, 2062–2068.

Murphy,A.H.,1973:A new vector partition of the probability score.J.Appl.Meteor.,12,595–600.

Palatella,L.,and A.Trevisan,2015:Interaction of Lyapunov vectors in the formulation of the nonlinear extension of the Kalman filter.Physical Review E,91,042905.

Pe˜na,M.,and Z.Toth,2014:Estimation of analysis and forecast error variances.Tellus A,66,21767.

Stephenson,D.B.,C.A.S.Coelho,and I.T.Jolliff e,2008:Two extra components in the Brier Score decomposition.Mon.Wea.Rev.,23,752–757.

Toth,Z.,and E.Kalnay,1993:Ensemble forecasting at NMC: The generation of perturbations.Bull.Amer.Meteor.Soc.,74, 2317–2330.

Toth,Z.,and E.Kalnay,1997:Ensemble forecasting at NCEP and the breeding method.Mon.Wea.Rev.,125,3297–3319.

Trevisan,A.,and R.Legnani,1995:Transient error growth and local predictability:A study in the Lorenz system.Tellus A,47,103–117.

Trevisan,A.,and F.Uboldi,2004:Assimilation of standard and targeted observations within the unstable subspace of the observation-analysis-forecast cycle system.J.Atmos.Sci.,61, 103–113.

Trevisan,A.,and L.Palatella,2011:Chaos and weather forecasting:the role of the unstable subspace in predictability and state estimation problems.International Journal of Bifurcation and Chaos,21(12),3389–3415.

Vannitsem,S.,and C.Nicolis,1997:Lyapunov vectors and error growth patterns in aT21L3quasigeostrophic model.J.Atmos.Sci.,54,347–361.

Wang,X.,and C.H.Bishop,2003:A comparison of breeding and ensemble transform Kalman filterensemble forecast schemes.J.Atmos.Sci.,60,1140–1158.

Wei,M.Z.,Z.Toth,R.Wobus,Y.J.Zhu,C.H.Bishop,and X.G. Wang,2006:Ensembletransform Kalman filter-basedensemble perturbations in an operational global prediction system at NCEP.Tellus A,58,28–44.

Wei,M.Z.,Z.Toth,R.Wobus,and Y.J.Zhu,2008:Initial perturbations based on the ensemble transform(ET)technique in the NCEP global operational forecast system.Tellus A,60, 62–79.

Wolf,A.,J.B.Swift,H.L.Swinney,and J.A.Vastano,1985:Determining Lyapunov exponents from a time series.Physica D,16,285–317.

Yoden,S.,and M.Nomura,1993:Finite-time Lyapunov stability analysis and its application to atmospheric predictability.J. Atmos.Sci.,50,1531–1543.

Zhang,J.,W.S.Duan,and X.F.Zhi,2015:Using CMIP5 model outputs to investigate the initial errors that cause the“spring predictability barrier”for El Ni˜no events.Science China Earth Sciences,58(5),685–696.

Ziehmann,C.,L.A.Smith,and J.Kurths,2000:Localized Lyapunov exponents and the prediction of predictability.Physics Letters A,271,237–251.

:Feng,J.,R.Q.Ding,J.P.Li,and D.Q.Liu,2016:Comparison of nonlinear local Lyapunov vectors with bred vectors,random perturbations and ensemble transform Kalman filter strategies in a barotropic model.Adv.Atmos.Sci.,33(9), 1036–1046,

10.1007/s00376-016-6003-4.

∗Corresponding author:Jianping LI

Email:ljp@bnu.edu.cn