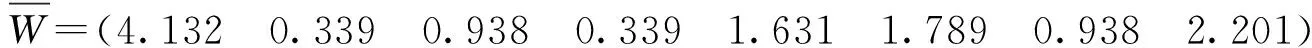基于组合权重模糊综合评价的建筑工程安全评价研究

刘志胜，王宏辉

(兰州交通大学 土木工程学院，甘肃 兰州　730071)



基于组合权重模糊综合评价的建筑工程安全评价研究

刘志胜，王宏辉

(兰州交通大学 土木工程学院，甘肃 兰州730071)

摘要：通过建筑施工过程安全管理分析，建立建筑施工安全评价指标体系，并结合层次分析法和熵权法形成组合权重，将与模糊综合评价法相结合建立模糊建筑工程安全评价模型，对建筑工程施工过程安全管理进行评价。评定工程施工管理安全等级，找出主要因素指标，提出安全管理意见。研究表明，该方法具有一定的客观性，有利于促进建筑安全管理目标的实现。

关键词：建筑工程；层次分析法；熵权法；安全评价；模糊综合评价法

1建筑安全评价体系的建立

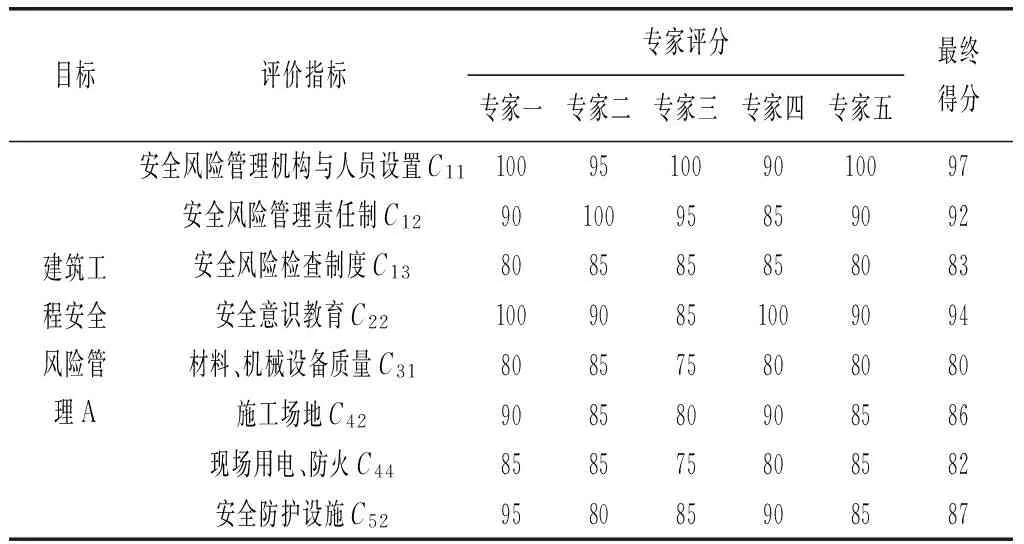
建立一个合理的评价指标体系是对建筑工程安全评价的基础，指标的选取是否合理，将直接关系到评价结果。为了了解全面的对建筑工程安全管理效果进行评价，对建筑工程安全风险管理效果进行评价，对建筑工程安全风险管理的主要内容和影响因素的具体分析，在参阅大量参考文献和施工单位安全管理文件资料以及与建设单位安全管理人员的交流探讨的基础上，将安全评价指标分为一级指标5个，二级指标18个，具体如表1所示。

表1　安全评价指标体系

较多的指标可以避免信息的遗漏并且更加全面的对建筑工程安全进行评价，但是较多的指标会增加了问题的复杂性，同时由于各个指标是对同一个事物的反映，所以存在不可避免的造成大量信息的重叠。故有必要对上述18个指标进行简化处理，精选出安全评价的最佳指标体系，共8个指标，具体见表2。

表2　简化后安全评价指标体系

2组合权重模糊评价法

2.1组合权重法确定权重

2.1.1层次分析法(AHP)确定主观权重向量

具体计算步骤如下所示。

(1)计算判断矩阵A每一行元素的乘积Wij：

(1)

(2)计算Wij的n次方根：

(2)

(3)对Wij归一化处理，可得：

(3)

则W=(w1,w2,…,wn)T即为所求的特征向量。

(4)计算判断矩阵的最大特征根λmax：

(4)

(5)一致性检验，先计算CI，即CI=(λ-n)/n-1。计算一致性比例，CR=CI/RI，当CR<0.10时，则可认为判断该矩阵的一致性是可以接受的，否则需对判断矩阵进行修改。

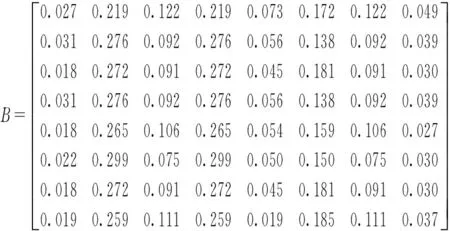
2.1.2熵权法确定客观向量。

在信息论中熵值可以表示信息量大小和反映信息的无序化程度等。其公式为

(5)

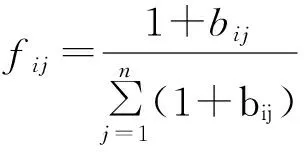
(6)

式中可以看出：熵值Hi越大，熵权Wd越小。

2.1.3确定组合权重W

组合权重计算公式为

(7)

式中：Wbm为熵权法各指标权重；Wdm为层次分析法各指标权重；Wzm为组合权重各指标权重。

2.2模糊数学法确定模糊矩阵

2.2.1评价因素集的建立

根据表2安全评价指标选取，建立综合评价因素U，U={u1，u2，…，un}

2.2.2评价集的建立

评价集为评价者对所评价对象可能做出的各种评价的集合V，即V={v1，v2，…，vn}。根据建筑施工安全实际情况，本文为安全评价中取n=4，即评价结果共有四种：①建筑安全管理体系完善为“优”；②安全管理体系建设基本完善为“良”；③安全管理体系中存在些问题为“中”；④安全管理体系中存在许多漏洞为“差”，故评价集V={优；良；中；差}。

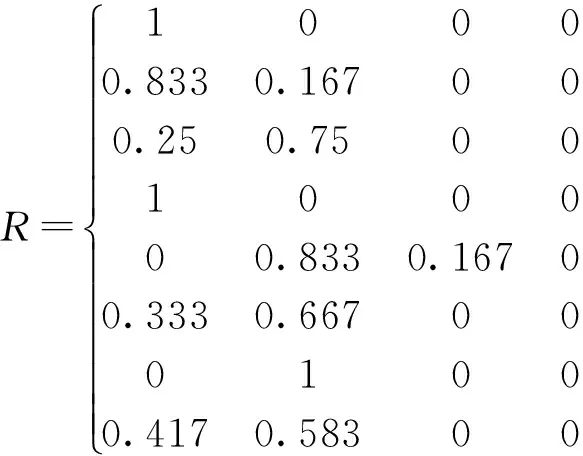
2.2.3隶属度函数的建立

矩阵R中元素Rij表示从第i个因素出发，对评价问题做出第j中评语的可能程度。

当j=1时，隶属函数为：

当1

当j=n时，隶属函数为

(8)

根据上列公式可求出隶属度，其表示为Rnm，结果为一个模糊集合R，由此得到评价矩阵为：

2.2.4综合评价

将组合权重Wzm与R进行综合运算，即可得到模糊综合评价结果为B=Wzm·R。最大综合隶属度所在的级别即为安全等级。

3实例分析

3.1确定评价指标评分值

为每一个评价指标设计一个评分表，请五位评估专家根据工程的实际情况对评价指标进行评分，其中最终得分为每个专家评分的平均值，如表3所示。

表3　评价指标评分值

3.2层次分析法确定权重

根据施工单位安全生产评价标准和施工安全数据统计，利用1～9级及其倒数的评定标度来构造判断矩阵，见表4。

表4　判断矩阵

根据公式(1)、(2)可得

归一化处理后得特征向量

Wbm=(0.3350.0280.0760.0280.1330.1450.0760.179)

3.3熵权法确定权重

对判断矩阵A归一化处理后，得到判断矩阵B为：

根据公式(5)、(6)计算权重向量为：

Wdm=(0.1750.1070.1160.1070.0980.1370.1160.144)

3.4确定组合权重

根据公式(7)可计算组合权重为：

Wzm=(0.2540.0580.0980.0580.1190.1470.0980.168)

3.5模糊数学法建立模糊矩阵

3.5.1建立模糊矩阵

根据建立的因素集和评价集以及隶属度计算公式(8)，可得模糊矩阵R，即

3.5.2综合评价

根据组合权重Wzm和模糊矩阵R进行运算，综合评价选区的隶属度为

B=Wzm·R=(0.5040.4760.020)

由综合评价结果B可以看出，安全评价的隶属度最大0.504，则该工程的模糊评价结果为优。但0.504与0.476相差无几，说明该工程安全管理有进一步改进和加强的必要。由于安全风险管理机构与人员设置和安全防护设施的组合权重值大，故应加强这两方面的规范管理，进一步提高施工安全保障。

参考文献：

[1]刘伟.赣南建筑工程安全事故致因分析及安全水平模糊综合评价的研究与实践[D].江西理工大学,2011:1-2.

[2]袁宁，杨立兵.基于粗糙集-人工神经网络的建筑施工安全评价及应用[J].安全与坏境工程,2012,19(1):59-64.

[3]李丽.高层建筑施工安全管理评价研究[J].工程管理,2015,14(1),50-53.

[4]乔雨，梁秀娟.组合权重模糊数学法在水质评价中的应用[J].人民黄河,2015,37(5):77-79

收稿日期：2015-11-05

作者简介：刘志胜(1988-)，男，硕士研究生，研究方向：工程造价。

中图分类号：U492

文献标识码：C

文章编号：1008-3383(2016)06-0167-02