基于弱匹配典型相关性分析的阿尔茨海默病识别

郝　杰　张　博　朱　红　马金凤　张昌明

(徐州医科大学医学信息学院，江苏　徐州　221000)



基于弱匹配典型相关性分析的阿尔茨海默病识别

郝杰张博1，2，3朱红马金凤张昌明

(徐州医科大学医学信息学院，江苏徐州221000)

〔摘要〕目的为了增强阿尔茨海默病(AD)的识别能力。方法该文采用多模态异构生物标志物数据在统计意义上潜在的相关性，利用互补原理，最大化不同模态数据之间的相关性，并在典型相关性分析的基础上，引入流形正则化技术提出了弱匹配典型相关性分析算法。结果解决了弱匹配多模态数据相关性建模问题。结论多模态异构生物标志物数据融合方法的预测性能优于单模态，能对AD的发病和病理研究提供更准确的信息。

〔关键词〕阿尔茨海默病；多模态数据融合；典型相关性分析；弱匹配多模态数据

老年认知障碍逐年增多，其中最常见的阿尔茨海默病(AD)，AD是一种进行性发展的致死性神经退行性疾病，通常被认为是由于脑疾病等原因造成神经细胞和神经元突触的大量丧失所导致〔1，2〕。轻度认知障碍(MCI)被广泛认为是AD与正常老龄化之间的一种过渡状态〔3～5〕。MCI状态并不是一个稳定的中间状态，病情有可能好转，也有可能发展成为完全的AD。有研究报道，每年由MCI转化成AD的比例约为10%～15%〔6〕。因此，对MCI的早期诊断与早期干预是临床诊疗工作的关键，延缓MCI向AD的转化速度，可降低患病率、死亡率，有效地提高患者的存活率和患者的生活质量。目前，大部分研究使用单模态分析法研究神经影像数据或其他生物标志物。所谓的单模态分析是指利用从单一信息渠道获得的观察样本进行识别的技术，如使用主成分分析(PCA)分析正电子发射断层扫描(PET)脑显像，使用独立成分分析(ICA)分析功能磁共振成像(MRI)数据。这些研究都是将AD群体和MCI群体的脑结构与正常老年人的脑结构相比，分析其脑结构的异常，评价从正常的认知老龄化到MCI、从MCI到轻度的AD和从轻度到重度痴呆这一过程的进展，以及利用这些标记物做早期诊断。然而，单模态数据的统计分析存在以下问题①许多生物标志物研究是基于以往临床标准诊断的病例，病例选择的准确性直接关系到单一标志物验证的准确性；②部分生物标志物在许多非AD人群也会出现，如斑块和缠结，需要大量纵向观察才能得出这些标志物在认知正常者中存在的意义和预测价值的客观结论，这需要付出大量的资金和人力成本。不同类型的生物标志物特征之间存在着关联信息。这些信息作为一种附加特征是有效且重要的，它们能在对AD预测和诊断的过程中有效地完成信息的互补和增强。本文采用多模态异构生物标志物数据在统计意义上潜在的相关性，如MRI与PET的融合、MRI与脑脊液(CSF)或蛋白质组等非影像生物标志特征融合。利用互补原理，最大化不同模态数据之间的相关性，减少数据之间的不确定性，从而达到增强识别能力的目的。由于在生物标记物的开发使用中，多个指标联合使用会比单个指标更有优势，所以通过多模态异构数据源的融合，可以对AD的发病和病理研究提供更准确的信息，同时也能在发病前，至少是发病的早期阶段预测到认知功能的下降。

1资料与方法

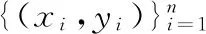
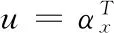
其中，

cxx=XXT∈Rp×Rp和cyy=YYT∈Rq×Rq

表示集合内协方差矩阵，cxy=XYT∈Rp×Rq表示集合间协方差矩阵，且Cyx=CxyT。

常将CCA问题等价地描述为以下特征值问题：

1.2弱匹配多模态数据的相关性建模在生物医学研究中，数据不完整的样本无处不在。如本文实验中使用的ADNI数据库，超过一半的受试者缺少CSF数据，还有很多的受试者没有FDG-PET或蛋白质组学数据。如图1所示，819组样本中，只有203份数据完整的样本，1～199号样本缺少CSF数据，403～819号样本缺少PET数据，609～819号样本只有MRI数据。数据缺失的原因很多，可能是由于某些检查的成本过高(如PET扫描)或属有创性检查(如CSF需要腰椎穿刺)，不是所有的研究参与者都愿意参与，也可能是一些长期的纵向随访研究中，研究参与者可能会错过定期评价中的一些科目或者受试者中途退出等。

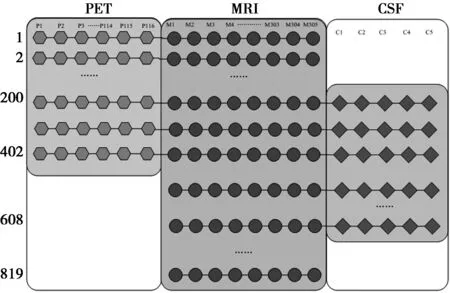
图1　ADNI数据库——819组患者样本

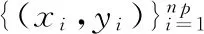
CCA中两组相关的随机变量可以来自多种信息来源(如同一个人的声音和图像)，也可以是从同一来源的信息中抽取的不同特特征(如图像的颜色特征和纹理特征)，但训练数据必须一对一严格匹配。面向弱匹配多模态数据的CCA有两种基本的方法：①丢弃未匹配数据，只使用CCA处理严格匹配的多模态数据；②根据特定准则，匹配多模态数据。但这两种方法都无法获得理想的结果。

为了解决弱匹配多模态数据相关性建模问题，本文使用流形正则化技术改进CCA，提出了弱匹配算法。弱匹配CCA算法构造了以下优化问题：

(1)

s.t.

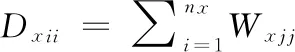
1.3弱匹配CCA求解方法弱匹配CCA算法的求解过程描述如下。为解式(1)，使用Lagrange乘子法。令：

(2)

(3)

用αT和βT分别乘以式(3)两边，得：

(4)

由式(4)得：

λ2=λ1

记λ2=λ1=λ，式(3)表示为以下矩阵形式：

(5)

式(5)是一个典型的广义特征值问题，可以直接进行求解。只要对矩阵进行特征值分解，依次取大特征值对应的特征向量，便可得到最终的典型(投影)向量。

求得d阶典型(投影)向量和后，对于任意样本，即可用如下方式进行特征融合：

ATx+BTy

(6)

(7)

其中A=〔α1,α2,···,αd〕,B=〔β1,β2,···,βd〕,d≤min(p,q)。基于式(6)和式(7)的特征组合方法分别简称为“并行组合”与“串行组合”。组合后的特征可用于任何分类器进行分类，本文中采用随机森林算法。

2结果

本文首先通过一个简单的模拟数据实验直观地考察经过弱匹配CCA算法降维后的组合特征对分类效果的影响，然后在ADNI数据库上检验弱匹配CCA算法降维后对正常老年人、MCI群体和AD群体识别能力的影响。

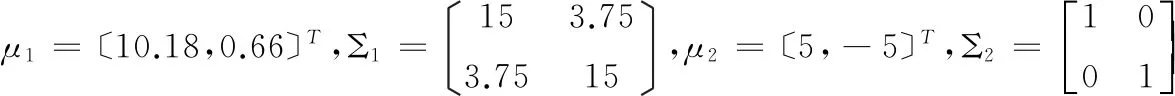
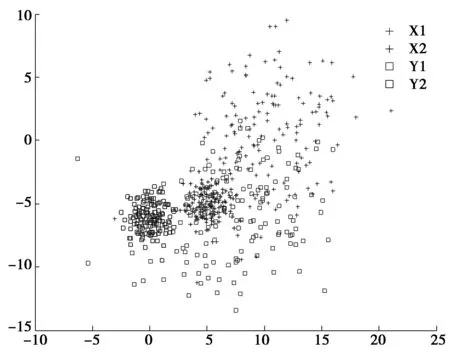
+：第一类样本；□第二类样本，下图同图2　二维样本的分布情况

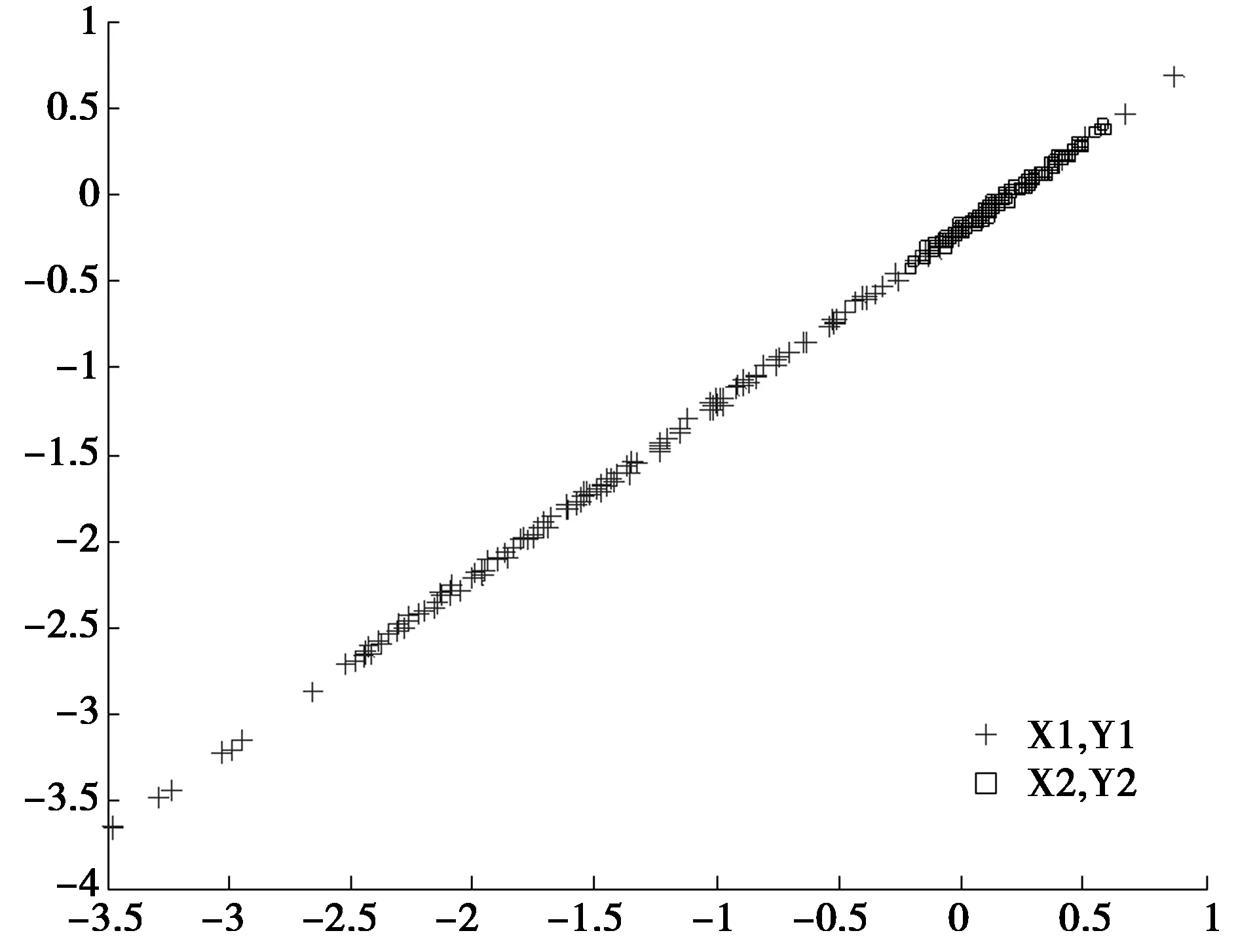
图3　原始数据集与经CCA降维后对组合特征的分布

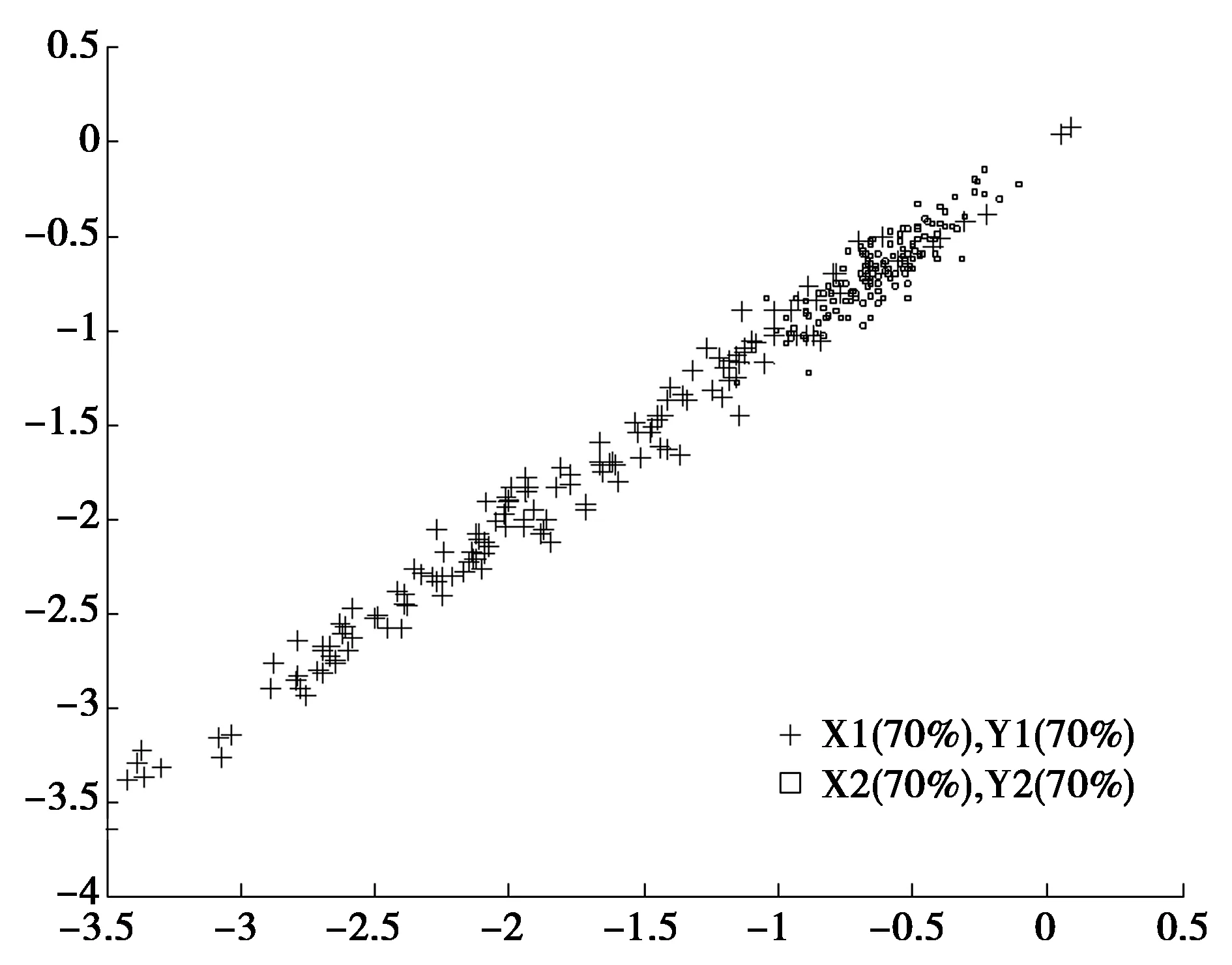
图4　CCA提取第一对组合特征的分布

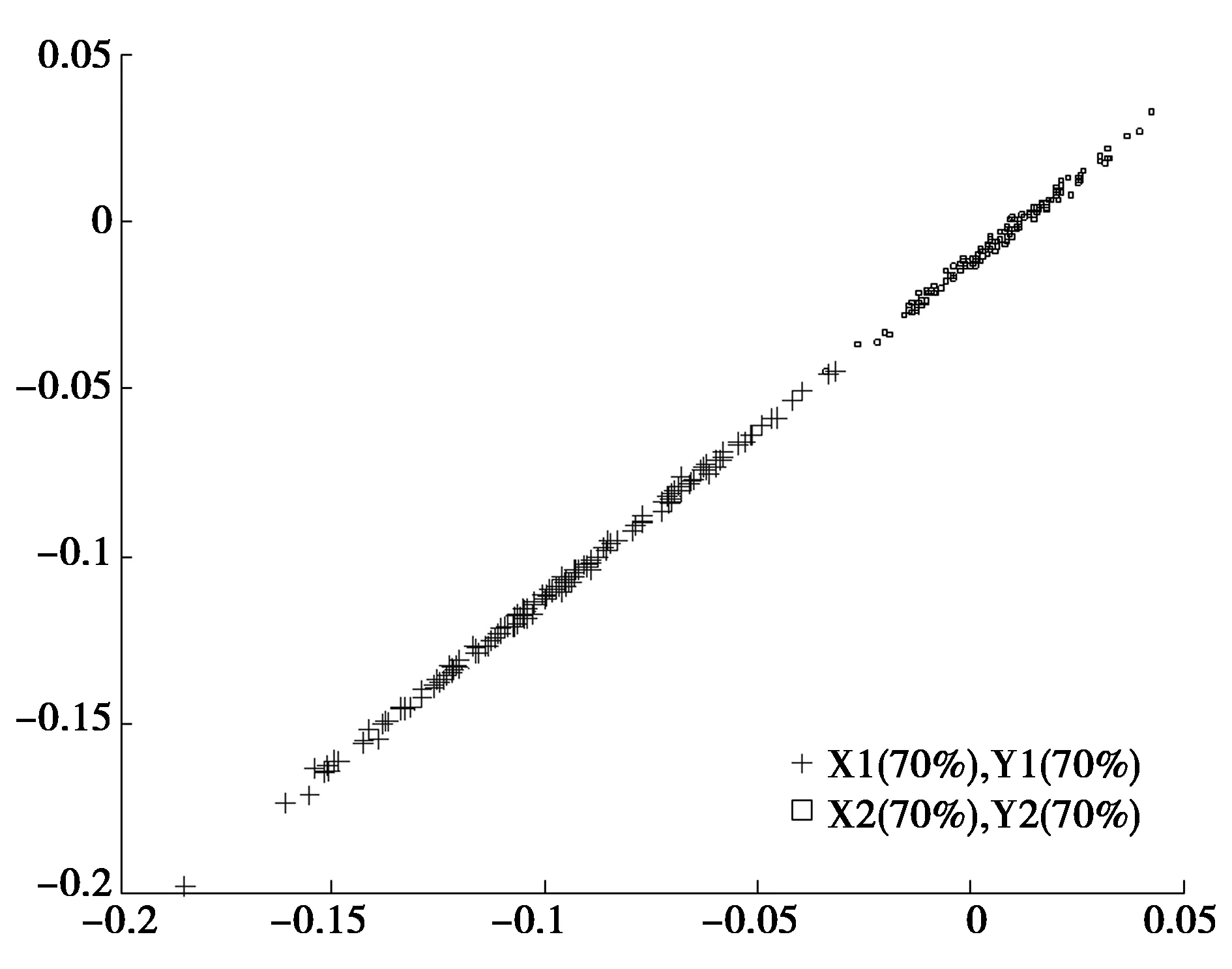
图5　弱匹配CCA提取第一对组合特征的分布

可以看出：①CCA揭示了特征之间的线性关系，但降维后两类之间存在一定程度的重叠，不利于分类；②在缺少30%样本的情况下，CCA出现了过拟合现象，样本间的相关程度降低；③在弱匹配CCA算法实验中，由于引入了各模态全部样本集合中蕴含的内部结构信息，获得了较为理想的结果，同时WXij的计算过程使得同类样本尽可能地靠近，不同类样本尽可能远离，所以两类样本可以被较好地分开。实验结果表明，弱匹配CCA算法提取的特征有利于分类。

2.2AD识别实验本文中，实验数据都是来自于ADNI数据库。ADNI是有史以来规模最大的医学影像学项目之一，其数据库涉及正常老年人、MCI群体和AD群体的结构磁共振成像(sMRI)，功能磁共振成像(fMRI)和PET等脑影像数据和血液、脊髓、年龄、性别、患病时间和临床评分等各种生物指标。ADNI项目始于2004年10月，其数据库不断更新。ADNI项目的主要目的是通过脑影像的综合研究来了解MCI与早期AD的发病历程，试图找出有效的临床治疗方案和预防措施。有关ADNI数据库的具体介绍请登录网站查询(其网站链接为http://adni.loni.ucla.edu/)。

2.2.1特征提取实验中使用ADNI数据库提供的819份样本(193例AD患者，397例MCI患者，229例正常人)建立AD分类模型。MRI脑影像数据的预处理使用基于Ubuntu操作系统的Maltab 7.0平台下的Statistical Parametric Mapping(SPM5，http：//www.fil.ion.uel.ae.uk/spm)软件包，对原始数据进行空间标准化，把原始的结构脑影像配准到标准空间中，然后对配准好的图像进行组织分割，去除非脑组织后，把脑组织分割成灰质、白质和脑脊液三部分，提取305为特征向量。对PET图像，使用AAL(Automated Anatomical Labeling)算法提取116维ACOI兴趣点作为特征向量。CSF数据提取Aβ1～42浓度、t-tau和p-tau水平以及t-tau/Aβ1～42、p-tau/Aβ1～42组成5维特征向量。见图6。

图6　特征向量提取

2.2.2实验设置和结果分析MRI特征集和PET特征集，分别使用PCA降维至50维，典型向量的阶数设置为5，10，15，…50。使用“串行”融合策略生成最终的分类特征。分类基于随机森林算法(Random Forests)〔9〕，直接使用Random forest-matlab软件包 。

为了对比分析，本文选取了3种比例的数据作为训练集，剩余进行测试，进行50次实验取均值。实验结果如表1～表3所示，列出了单特征方法，两组和三组异构特征融合方法、弱匹配CCA融合分类结果。对该组实验结果的分析：①由于多个指标联合使用会比单个指标更有优势，所以较之单特征方法，两组或三组异构特征融合的方法具有一定的识别优势。②相对于单特征方法与异构特征融合的方法，弱匹配CCA融合的方法具有显著的识别优势。而且，这表明，弱匹配CCA直接提取了各异构特征间的综合相关特征，最大化了不同模态数据之间的相关性，同时减少数据之间的不确定性，使相同类型的样本尽可能靠近，不同类型的样本尽可能远离，从而达到增强识别能力的目的。因此具有更高的分类精度。③整体而言，各方法分类精度随着训练集中样本数量的增加而提高。

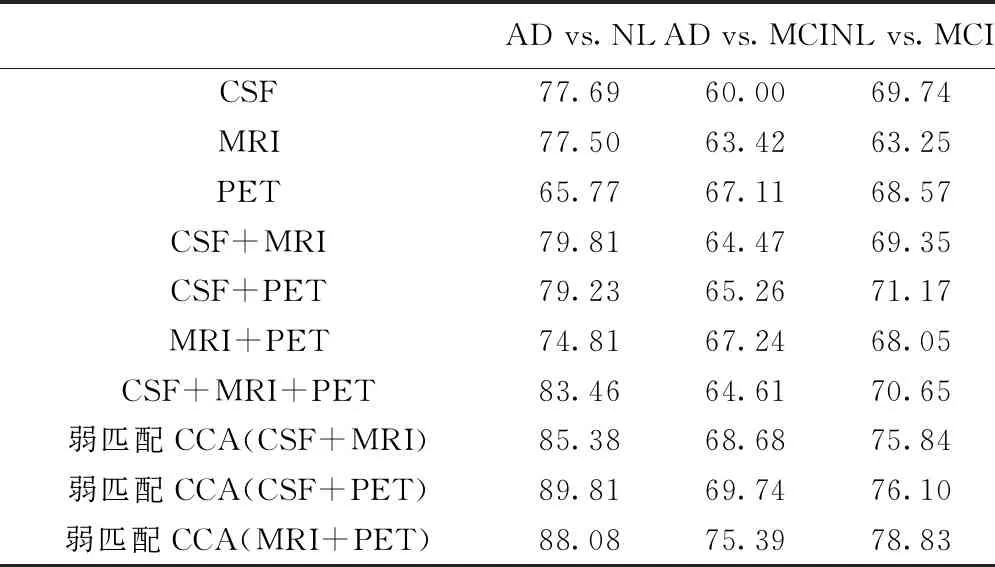
表1　训练集大小50%的分类准确率(%)

AD：AD患者；NL：正常人群；MCI：MCI患者，下表同

表2　训练集大小66.7%的分类准确率(%)

表3　训练集大小75%的分类准确率(%)

3讨论

与传统单模态分析法研究神经影像数据或其他生物标志物的方法不同，本文使用弱匹配CCA方法分析多模态异构生物标志物数据在统计意义上潜在的相关性，最大化不同模态数据之间的相关性，同时减少数据之间的不确定性，使相同类型的样本尽可能靠近，不同类型的样本尽可能远离，从而达到增强识别能力的目的。本实验表明，在生物标记物的开发使用中，多个指标联合使用会比单个指标更有优势，而且通过弱匹配CCA方法对各模态异构数据源的融合，可以对AD的发病和病理研究提供更准确的信息，同时也能在发病前，至少是发病的早期阶段预测到认知功能的下降。多重集典型相关性分析(MCCA)是CCA向多个数据集的自然推广，用于分析多个(多于2个)数据集合变量间的线性关系。1971年Kettenring〔10〕提出了一系列的MCCA，并给出了迭代解法。2003年Yamanishi等〔11〕提出了多重集的核典型相关性分析(MKCCA)，用于提取多基因组的相关性。

4参考文献

1Terry RD，Masliah E，Salmon DP，etal.Physical basis of cognitive alterations in Alzheimer′s disease：synapse loss is the major correlate of cognitive impairment〔J〕.Ann Neurol，1991；4(30)：572-80.

2Wenk GL.Neuropathologic changes in Alzheimer′s disease〔J〕.J Clin Psychiatry，2003；(64)：7-10.

3Petersen RC，Smith GE，Waring SC，etal.Mild cognitive impairment：clinical characterization and outcome〔J〕.Arch Neurol，1999；56(3)：303-8.

4Morris JC，Storandt M，Miller JP，etal.Mild cognitive impairment represents early-stage Alzheimer disease〔J〕.Arch Neurol，2001；58(3)：397-405.

5Rombouts SARB，Barkhof F，Goekoop R，etal.Altered resting state networks in mild cognitive impairment and mild Alzheimer′s disease：An fMRI study〔Z〕.Wiley Subscription Services，Inc.，A Wiley Company，2005:231-9.

6Grundman M，Petersen RC，Ferris SH，etal.Mild cognitive impairment can be distinguished from Alzheimer disease and normal aging for clinical trials〔J〕.Arch Neurol,2004；61(6)：59-66.

7Belkin M，Niyogi P，Sindhwani V.Manifold regularization：a geometric framework for learning from labeled and unlabeled examples〔J〕.J Mach Learning，2006；7：2399-434.

8彭岩，张道强.半监督典型相关分析算法〔J〕.软件学报，2008；19(11)：2822-32.

9Liaw A，Wiener M.Classification and regression by random forest〔J〕.R News，2002；2(3)：18-22.

10Kettenring J.Canonical analysis of several sets of variables〔J〕.Biometrika，1971；(58)：433-51.

11Yamanishi Y，Vert JP，Nakaya A，etal.Extraction of correlated gene clusters from multiple genomic data by generalized kernel canonical correlation analysis〔J〕.Bioinformatics,2003；19(Suppl 1)：i323-30.

〔2014-12-06修回〕

(编辑赵慧玲/曹梦园)

通讯作者：朱红(1970-)，女，副教授，博士，主要从事属性约简、聚类分析、粒度计算研究。

〔中图分类号〕TP391

〔文献标识码〕A

〔文章编号〕1005-9202(2016)13-3259-05；

doi：10.3969/j.issn.1005-9202.2016.13.081

1中国科学院计算技术研究所智能信息处理重点实验室

2中国矿业大学计算机科学与技术学院3中国科学院研究生院

第一作者：郝杰(1980-)，女，副教授，硕士，主要从事人工智能、机器学习研究。