基于改进遗传算法的带时间窗车辆路径问题研究*

黄务兰，张　涛

(1.上海财经大学 信息管理与工程学院,上海 200433； 2.常州大学 商学院, 江苏 常州 213164；3.上海财经大学 上海市金融信息技术研究重点实验室，上海 200433)



基于改进遗传算法的带时间窗车辆路径问题研究*

黄务兰1,2，张涛1,3

(1.上海财经大学 信息管理与工程学院,上海 200433； 2.常州大学 商学院, 江苏 常州 213164；3.上海财经大学 上海市金融信息技术研究重点实验室，上海 200433)

摘要：该文以最小化配送时间为目标，研究带时间窗的车辆路径问题，建立整数规划模型。为了加快遗传算法的收敛速度和寻优能力，提出一种改进遗法算法IGALS (Improved Genetic Algorithm with Local Search)。改进算法借用精英保留策略，采用点交叉和段交叉算子结合的交叉算子；提出路段允许延迟时间概念，并以此为依据使用局部搜索策略进一步提高解的质量。通过Solomon标准算例测试，验证了改进算法(IGALS)较简单遗传算法(GA)具有更好的全局寻优能力和更快的收敛速度。

关键词：带时间窗车辆路径问题；遗传算法；交叉算子；局部搜索；整数规划

引用格式：黄务兰，张涛. 基于改进遗传算法的带时间窗车辆路径问题研究[J].微型机与应用，2016,35(13)：21-24.

0引言

车辆路径问题(Vehicle Route Problem，VRP)的研究最早由DANTZIG G和RAMSER J于1959年提出[1]，近60年来始终是运筹学与组合优化领域的研究热点，受到了国内外研究者的广泛关注。为了满足实际需求，学者对VRP问题逐步进行了扩展和变形。其中带时间窗车辆路径问题(Vehicle Route Problem with Time Windows，VRPTW)是在车辆路径问题的基础上加入了时间窗约束。加入时间窗后，极大地增加了VRP问题计算难度和复杂度，除了考虑VRP问题空间方面的路径之外，还必须考虑时间上的排程，因此吸引了许多国内外学者对其进行研究，成为VRP问题研究领域最热门的研究方向之一[2-4]。本文研究带时间窗路径优化问题，以最小化配送时间为目标建立路径优化数学模型，借用精英策略思想设计交叉算子提高遗传算法的寻优性能，并使用基于延迟时间的局部搜索策略进一步提高解的质量。

1问题描述和数学建模

带时间窗车辆路径优化问题描述为：某快递配送中心拥有M辆型号相同且载重量为Q的配送车辆，为N个已知客户做派发快件服务。每个顾客服务位置和需求量已知，客户具有服务时间窗[ETi,LTi]，即最早和最迟开始服务时间，以及持续服务时间STi，如果车辆到达客户i的时间早于ETi，车辆需要在客户i处等待。现要求对该问题进行路径规划，要求在最小化成本的前提下配送完所有客户所花费的总时间最少。为了能更准确地表述模型，引入如下符号体系:M表示可供使用的最大车辆数；N表示客户数目；Q表示车辆的最大载重量；tij表示顾客i到顾客j的路由时间； [ETi,LTi]表示节点i的时间窗；ATi表示车辆到达节点i的时间；Si表示车辆k开始服务节点i的时间；WTi表示车辆在客户i处的闲置等待时间；STi表示顾客i持续服务时间，为已知量。

定义如下决策变量：

本文目标是合理安排配送路径，力求配送完所有客户所花费的总时间最少。其中，配送时间分为三部分：车辆的路由时间，可由式(1)表述；车辆因时间窗未开在客户处的等待时间，可由式(2)表述；服务客户的时间，因该时间是一已知量，与决策安排无关，因此不列入目标函数中。

(1)

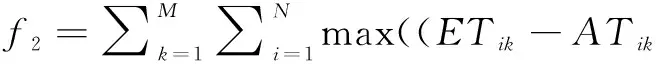
(2)

因此，总目标函数为:

Z=min(f1+f2)

(3)

并且满足:

(4)

(5)

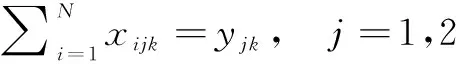
(6)

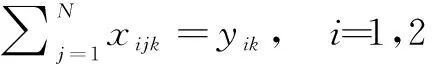
(7)

(8)

AT0=S0=ST0=0

(9)

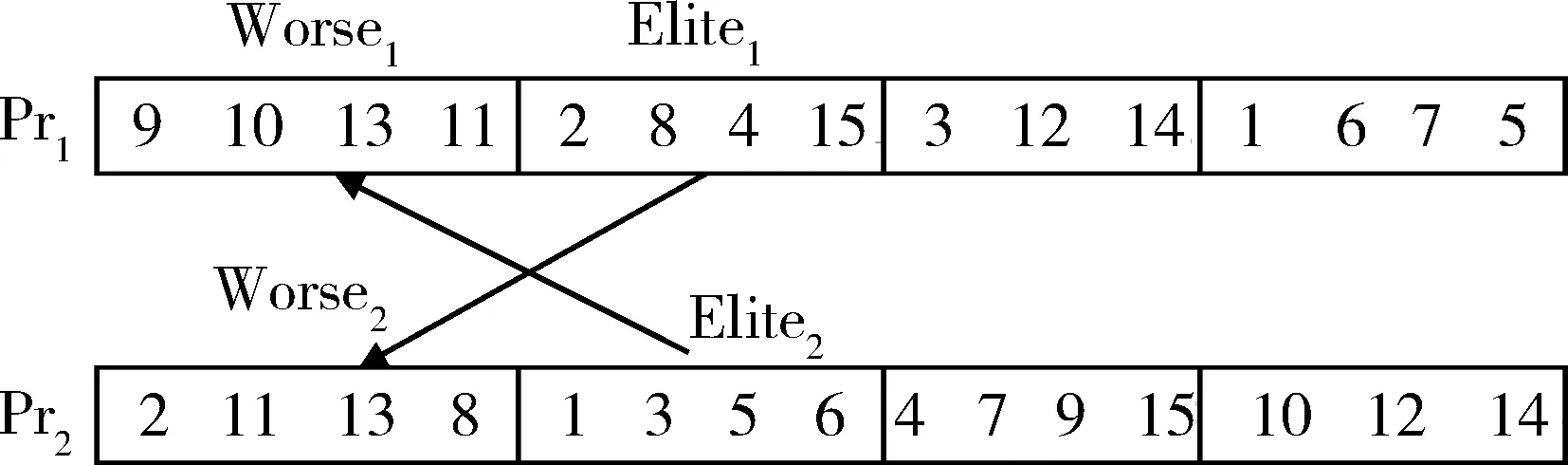
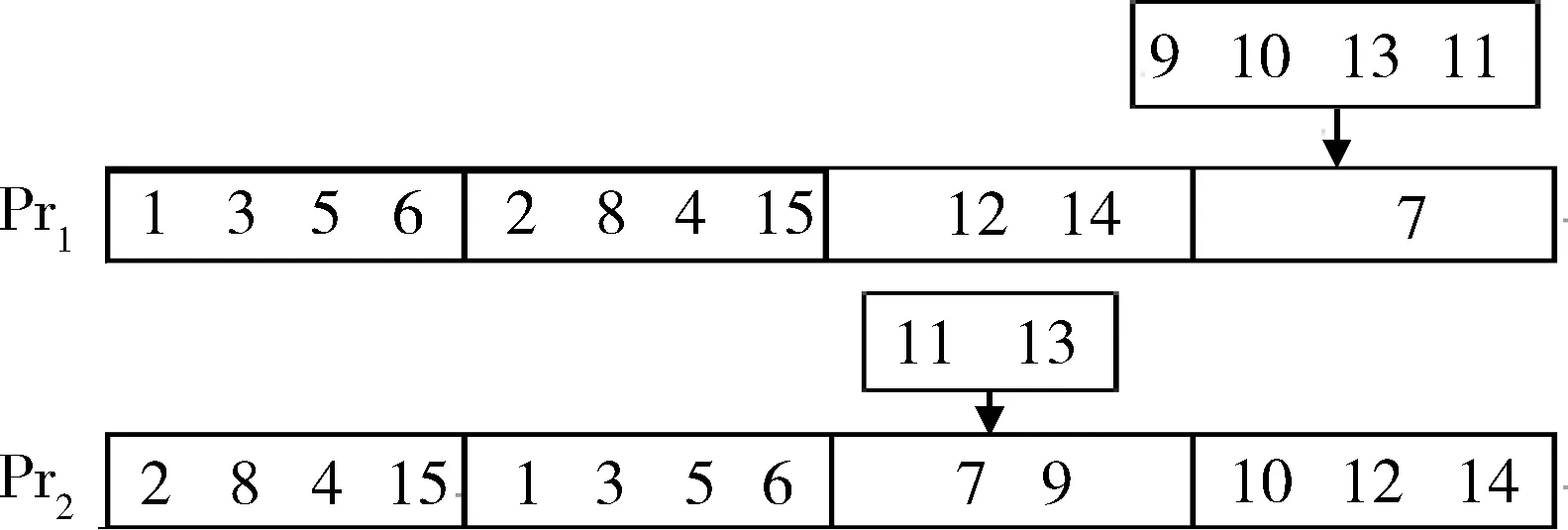
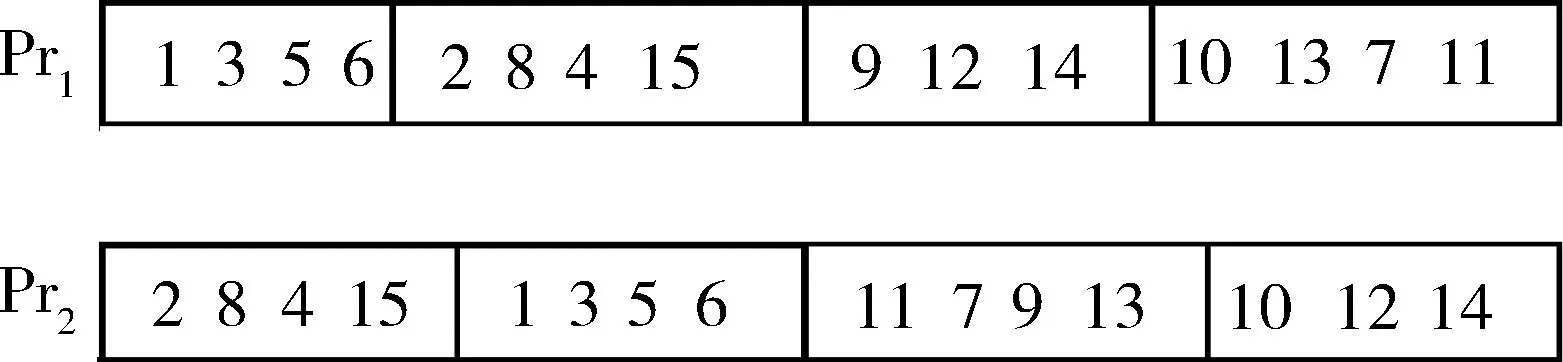
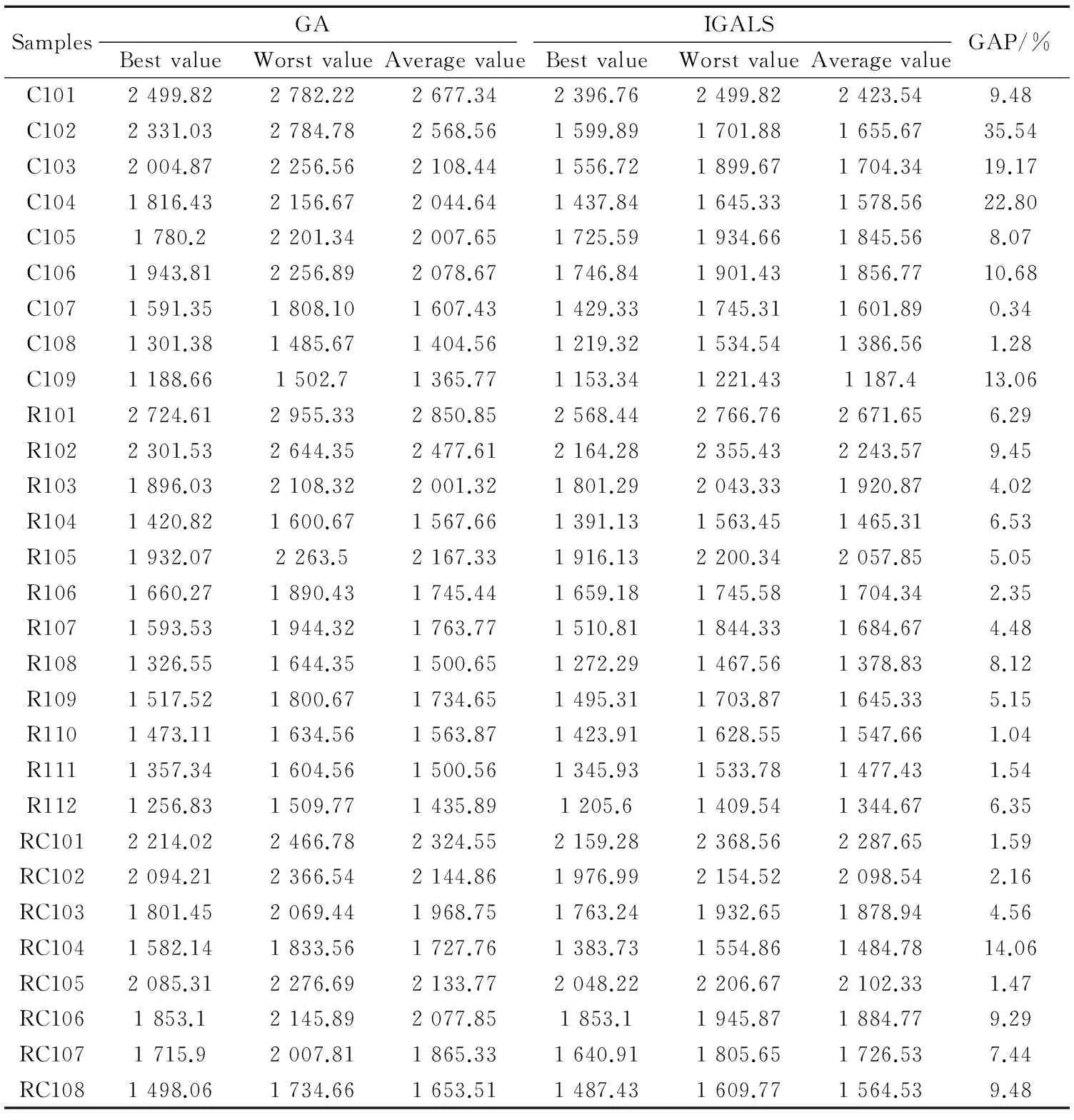
0

(10)

STi>0，i=1,2,...,N

(11)

(Si+STi+tij).xijk≤ATj，i=1,2,...,N,j=1,2,...,N,i≠j

(12)

ETi≤Si≤LTii=1,2,...N

(13)

(14)

xijk∈{0,1}i,j=0,1,2,...,N;k=1,2,...,M

(15)

yik∈{0,1}i=1,2,...,N;k=1,2,...,M

(16)

式(4)表示客户i只能由一辆车为其配送服务；式(5)表示配送中心最多发出M辆车；式(6)和式(7)表示两个变量之间的关系；式(8)确保每辆车承载的货物总量不超过其最大容量，且不为负；式(9)初始化到达配送中心时间、开始服务时间与持续服务时间都为0；式(10)表示车辆到达客户i的时间先于或等于开始服务时间，且为非负时间；式(11)表示顾客i的持续服务时间为正数；式(12)表示车辆由客户i到达客户j的时间计算公式，即前驱点与后继点的时间关系；式(13)表示服务客户i的时间应满足时间窗约束；式(14)表示实际开始服务客户i的时间计算方法； 式(15)和式(16)分别表示变量xijk和yik的取值范围为0或1。

2求解算法设计

2.1改进的交叉算子

遗传算法是由美国的HLLAND J H教授[5]最早提出的，是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法。本文结合实际问题，提出一种改进的遗传算法，称之为IGALS (Improved Genetic Algorithm with Local Search)。

本文采用点交叉和段交叉结合的方式，保证遗传算法种群的多样性。其中点交叉采用循环交叉方法，段交叉方法借用精英策略的思想。它将每辆车的行驶线路划分为一段，对每一段线路计算目标值。将单个种子某趟车目标值优的路线保留不变，同时借鉴参与交叉的另一种子中目标值优的某趟车路线来替换目标种子中目标值劣的某车辆路段，交换之后去掉重复节点，这样可以有目的地进一步优化目标种子的解。

设有15个节点，参与交叉的父代种子Pr1和Pr2，其中每个种子按单趟车辆线路划分为4段，种子内部适应值最优车辆线路标识为Elite1和Elite2，最坏适应值车辆路段分别标识为Worse1和Worse2，如图1所示。

图1　交叉种子示例

交叉过程中种子内部次序调整如下，即将最坏路段置为第一段，精英路段置为第二段，如图2所示。

图2　交叉过程1

最后，将交叉种子精英路段替换掉目标种子最坏路段，并去掉后面重复节点。交叉后的两种子如图3所示，其中“*”号表示去掉重复种子留下的空位。去掉目标种子的最坏路段节点，Pr2中的11、13节点是有待进行重新插入的节点，必要时进行重新排序的操作，交叉后的两种子如图4所示。

图3　交叉过程2

图4　交叉结果

2.2局部搜索策略

局部搜索算法也称大规模邻域搜索(Large Neighborhood Search，LNS)，是一类改正型算法，它是1998年由SHAW P[6]提出的，算法的每一步迭代都是通过搜索当前解的邻域得到一个改进的解。因时间窗约束，种子在迭代过程中解的质量并不十分理想。基于此，本文设计一种局部搜索(Local Search)策略，提出路段允许延迟时间概念，依据该指标，在可行线路中进行局部搜索，最大限度地减少节点等待时间，进一步优化遗传算法的求解性能，找到使目标值更优的解。

设有一条可行线路Routek(v0,v1,…,vi-1,vi,vi+1,…,vn,v0)，其中v0为配送中心，vi(i=1,2,3…n)为车辆要配送货物的客户点，已知客户i的时间窗[ETi，LTi]和配送中心时间窗[0,H]，车辆在vi点的持续服务时间STi，tij为车辆从i到j的时间，WTi为车辆在vi点的等待时间。

定义每个节点的最早完成时间Vei和最迟开始时间Vli，最早完成时间Vei表示车辆完成从v0到vi配送任务的最早时间，而最迟开始时间Vli表示车辆顺利完成vi到vn各点的配送任务，应在vi点开始作业的最晚开始时间。

表1　GA与IGALS的计算性能比较

Vei和Vli的计算方法如下：

Vei=max(ETi+STi,Vei-1+ti-1,i+STi)

(17)

Vli=min(LTi,Vli+1-ti,i+1-STi)

(18)

因车辆在配送中心无配送任务，ST0=0，故Ve0=ET0=0，Vl0=LT0=H，从Ve0=0开始依次计算Ve1、Ve2、…、Ven的值。从Vl0=H开始依次计算Vln，Vln-1，…，Vl1的值。

定义：相邻节点(vi,vj)即某一路段的允许延迟时间用DTij表示:

DTij=Vlj-Vei

(19)

(1)移除策略

①移除路由时间tij比较大的客户节点j将其从原始路线中移出；②移除等待时间WTj较大的客户节点j；③移除tij+WTj值较大的客户节点。

(2)重插策略

①将违反时间窗和载重量的位置排除，这些位置不能插入；②设有可行线路(v0,v1,…,vi-1,vi,vi+1,…，vn,v0)，将vj点插入vi-1到vi之间的充要条件是:

DTi-1,i≥ti-1,j+tji-ti-1,i+STj

(20)

很明显，采用该局部搜索策略会明显降低目标值中的等待时间，充分发挥寻优作用。

3仿真实验和数据分析

本文采用Solomon标准测试算例C1、R1、RC1型数据进行测试，它们具有时间范围较短，车辆容量较小的特点，适合模拟本文描述问题。

实验采用C++语言，在Visual Studio 2010集成开发环境中编写，程序运行在Win 7系统中的Intel Core-i5，2.5 GHz主频(6 GB内存)，64位的Laptop机上。车辆路由速度为单位速度，交叉概率pc=0.75，变异概率pm=0.10，种群规模设为100，表1是两种算法每个算例运行10次的结果，平均目标值为10次取平均的结果。可见，29组测试数据中，改进的混合遗法算法平均目标值全部优于简单遗传算法，最大改进率高达35.54%。改进的混合遗传算法使用局部搜索策略和精英交叉策略，加快了寻优速度，并能有效地避免算法陷入局部最优。

图5　R101算例最优解收敛曲线

算例R101最优结果的迭代过程如图5所示，横轴代表算法迭代次数，纵轴代表最优解的值。简单遗传算法在迭代20 000次左右陷入了局部最优解，最优值为2 724.61，可以看出算法的最大缺陷是“早熟”。改进的混合遗传算法前段收敛速度较快，其中迭代到16 000次左右遇到一个局部较优解，目标值为2 704.58，但是算法很快就跳出该解，最后求得一个更优解，目标值降到2 568.44。改进的混合遗传算法在后段能够跳出局部最优解，主要是局部搜索算法进一步寻优的结果。说明改进的混合遗传算法能够较好地避免“早熟”并有较快的收敛速度。

4结论

当前电子商务的快速发展带动了快递物流业的发展，影响快递服务质量的关键因素之一为快递配送时效。本文以最小化快递配送时间为目标，研究带时间窗的车辆路径问题，建立数学模型；为克服遗传算法收敛速度慢和早熟的缺陷，设计并采用了一种段交叉算子和基于延迟时间的局部搜索策略。通过Solomon标准算例测试表明，改进的混合遗传算法较简单遗传算法有较好的全局寻优能力，验证了本文算法的有效性。

参考文献

[1] DANTZIG G, RAMSER J. The truck dispatching problem[J].Management Science,1959, 6 (1): 80-91.

[2] SOLOMON M, DESROSIERS J.Time window constrained routing and scheduling problems: a survey[J].Transportation Science,1988,22(1):1-13.

[3] NAZIF H, LEE L S. Optimized crossover genetic algorithm for vehicle routing problem with time windows[J].American Journal of Applied Sciences,2010,7(1):95-101.

[4] 王君.带时间窗车辆路径问题的差分进化混合算法[J]. 计算机工程与应用, 2013，49(2):24-28.

[5] HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificialintelligence[M].Cambridge: University of Michigan Press,1975.

[6] SHAW P. Using constraint programming and local search methods to solve vehicle routing problem[M]. Springer Berlin Heidelberg, 1998, 1520:417-431.

*基金项目：国家自然科学基金(71171126)；教育部高等学校博士学科点专项科研基金(20130078110001)

中图分类号：TP301.6

文献标识码：A

DOI：10.19358/j.issn.1674- 7720.2016.13.007

(收稿日期：2016-03-01)

作者简介：

黄务兰(1979-)，通信作者,女，博士生，讲师，主要研究方向：智能优化算法,物流优化。E-mail:huangwulan@163.com。

张涛(1970-)，男，博士，教授，博导，主要研究方向：物流优化，金融大数据。

Vehicle routing problem with time windows based on improved genetic algorithm

Huang Wulan1,2，Zhang Tao1,3

(1.School of Information Management and Engineering, Shanghai University of Finance and Economics,Shanghai 200433,China；2. Business School of Changzhou University, Changzhou 213164,China； 3. Key Laboratory of Financial Information Technology,Shanghai University of Finance and Economics, Shanghai 200433, China)

Abstract:This paper studied the VRPTW (Vehicle Routing Problem with Time Windows). An integer programming model is constructed, its objective is to minimize the delivery time. To further improve the convergence speed and optimization capability of the genetic algorithm, an improved genetic algorithm with local search (IGALS) is proposed, which is based on a hybrid crossover operation with elitist strategy and a local search using the thought of allowed delay time. Testing by Solomon Benchmarks instances, the results show that the proposed hybrid genetic algorithm has better performance and faster convergence speed than simple genetic algorithm.

Key words:vehicle routing problem with time windows (VRPTW); genetic algorithm; crossover operator; local search; integer programming