208 000 DWT散货船机舱总段整体吊装强度有限元分析
刘 锐, 王 铭, 张 健, 何文心
(1.武昌船舶重工集团有限公司, 湖北 武汉 430060; 2. 上海外高桥造船有限公司, 上海 200137;3.江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003)
208 000 DWT散货船机舱总段整体吊装强度有限元分析
刘锐1, 王铭2,3, 张健3, 何文心3
(1.武昌船舶重工集团有限公司, 湖北 武汉 430060; 2. 上海外高桥造船有限公司, 上海 200137;3.江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003)
摘要整体吊装是船舶建造中的一项重要工艺。考虑到208 000 dwt散货船机舱总段结构本身的复杂性及船厂的需求,整体吊装时的结构响应只能以三维有限元方法进行模拟。本文在研究大型散货船机舱总段整体吊装工艺的基础上,分析了不同区域的吊码载荷历程曲线,运用有限元法对该吊装过程在起吊上升、移位运输以及下降三个不同阶段进行了动态数值仿真分析,得到了吊装引起的机舱总段应力及变形水平。通过有限元计算分析得到的相关结果可用于指导船舶机舱总段吊装方案的设计及优化,同时对吊码类型的选择和结构变形控制具有参考意义。
关键词机舱总段吊装强度吊码载荷有限元分析
0引言
现代造船模式的船体建造采用分段和总段建造法,分段吊装是船体总段进行船坞搭载的关键步骤,提高船体总段吊装技术对分段的完整性、缩短船坞周期、提高船舶建造质量有着重要的意义。
近几年来国内外学者对吊装技术研究主要是在上层建筑整体吊装方面,利用有限元软件进行强度校核计算,根据计算结果采取相应的加强措施。相应的研究都取得了较大的成果并应用到实际生产中,极大地提高了上层建筑吊装工艺水平,产生了一定的经济效益。机舱总段直接关联到主机的吊装,对分段预舾装水平、分段的完整性都有较高的要求。
以往研究所使用的有限元计算只能模拟仿真分段吊装的单一工况,无法对吊装的全程进行模拟仿真计算,如需要计算任意吊装工况,只能重新设置载荷、边界条件、约束等,给实际生产带来一定的不便。一般有限元软件计算都需要重新建模,而机舱总段存在很大的线型,建模需要花费大量的时间。本文所采用的软件不需要直接建模,从相应的软件中导入计算即可,节省了大量时间并提高了工作效率。
1机舱总段吊装情况概述
本文研究对象为208 000 dwt散货船机舱10A总段的搭载过程。10A总段由7个分段总组而成,沿船长方向长度为29.8 m,宽度为36.2 m,高7.8 m。其重量以及重心的具体信息如表1所示。由表可知,总段搭载阶段的舾装重量为131.3 t, 10 A搭载阶段的总重为715.80 t。

表1 10A总段重量及重心统计
根据总段的估算重量715.80 t超过了单台龙门吊吊装能力,集合生产场地的实际情况,采用两台600 t龙门吊抬吊的方式进行吊装。吊码布置形式及龙门起重机布置如图1所示。
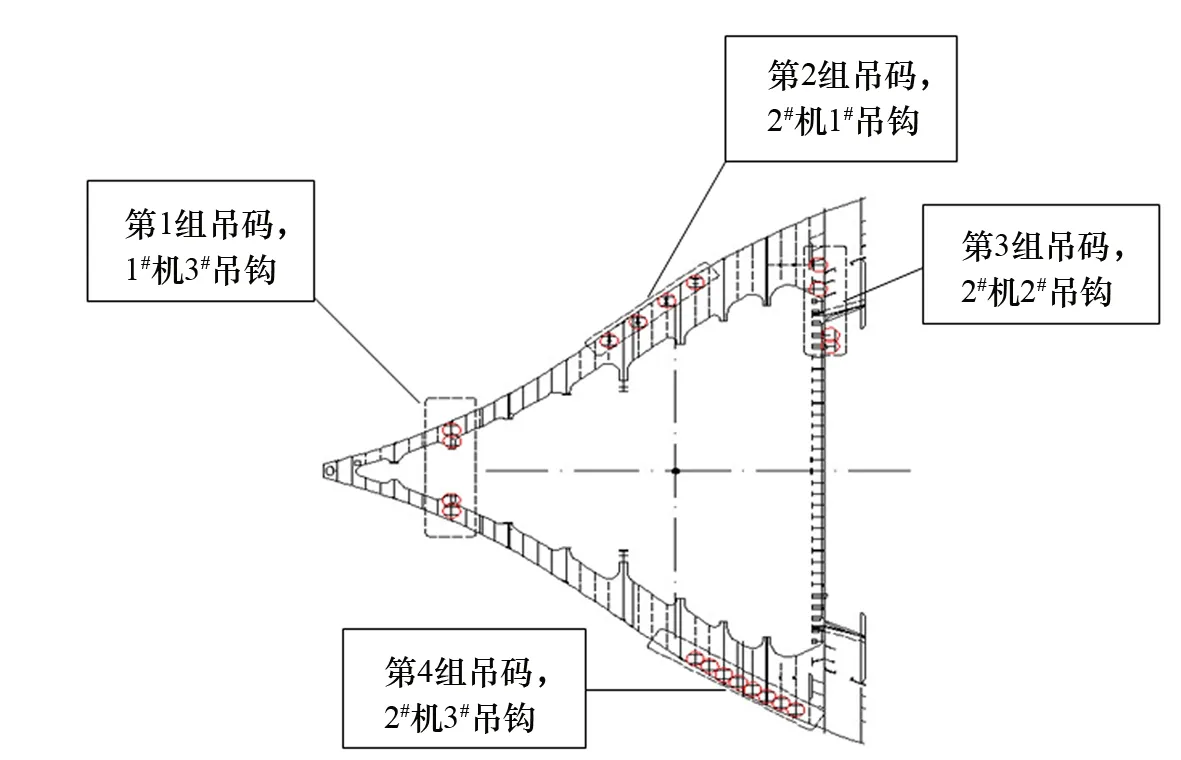
图1 10A总段吊码布置图
第1、4两组吊码编码由上至下依次进行,第2、3组吊码是由左向右依次进行编号,总段吊装过程如图2所示。两台600 t龙门吊抬吊分段最大重量为830 t(已扣除吊具重量)。抬吊时,两台龙门吊车大梁中线之间(沿船坞长度方向)最小距离为18 m,同时两台龙门吊上、下小车之间沿主梁方向(船坞宽度方向)最小距离必须大于11 m[2]。
2分段吊装计算方法研究
在吊装过程中,船舶分段在自身重力和钢丝绳拉力的共同作用下实现起升、下落和翻转等空间位置移动、姿态变化。考虑到吊装作业过程缓慢,被吊物体运动速度、加速度较小,再考虑到吊码、卸扣、钢丝绳存在一定的承载裕度,能够吸收一定的惯性力,因此对吊装过程中的动载荷给予忽略,仅对船舶分段在整个吊装过程中作静力平衡分析计算和校核[3]。

图2 10A总段吊装过程中的移位及落坞
一个物体在空间的活动具有六个自由度,其保持静力平衡的条件是在每一个自由度上所受的合力以及合力矩为零。在三维空间直角坐标系下,须满足以下平衡方程:
(1)
(2)
式中:FXi、FYi、FZi分别为Fi力在X、Y、Z轴方向上的分量;MXi、MYi、MZi分别为Mi弯矩在X、Y、Z轴方向上的分量。
设X、Y、Z轴位于水平面内,Z轴竖直向上,对船舶分段的吊装作业而言,通常在水平面内无沿X、Y方向的作用力,也无绕Z轴的作用力矩,因此船舶分段吊装过程的静力平衡方程简化为
(3)
若船舶某分段的重量为G,采用最常用的三钩起吊,以重心为原点建立坐标系,三个吊钩在水平面内距Y轴、X轴的距离(即吊钩的X、Y坐标)分别为X1、Y1、X1、Y1、X3、Y3(根据所在象限区分正负值),设三个吊钩所承受来自分段的拉力(不包含吊排重量)分别为F1、F2、F3,则受力平衡方程
(4)
该方程为关于F1、F2、F3的三元线性方程组,求解可解得各力。然后根据吊码数量以及吊码与钢丝绳的链接方式,再同样运用上述平衡方程即可求得每个吊码或卸扣所承受的拉力。
除最常用的三钩起吊方式外,船体结构件建造过程中还用到两钩起吊、四钩起吊方式。对于两钩起吊,受力状态简化为平面受力,用于求解三钩起吊问题的三元线性方程组退化为二元线性方程组,如下:
(5)
对于四钩起吊,拉力的数量变为四个,设各拉力为F1、F2、F3、F4,各自在水平面内距Y轴、X轴的距离(即吊钩的X、Y坐标)分别为X1、Y1、X2、Y2、X3、Y3、X4、Y4(根据所在象限区分正负值),受力平衡方程为
(6)
上述式(4)、(5)、(6)为船舶分段吊装设计力学计算的基本理论。三个方程式不仅可用于吊装方案设计初期的计算,也可用于对调整、优化后方案进行受力校核。
3机舱总段吊装有限元计算
3.1有限元模型
该分段模型为机舱总段模型,钢板材质为AH32,根据不同的板厚和加强形式分别赋予不同的属性。图3为有限元模型和厚度分布云图。应用MPC法对吊码受力进行模拟。
将龙门吊键入模型,并将吊点分布情况显示出来。通过观察模型的运动姿态,选取三个动态工况下的载荷,分别将三种载荷加载到模型中进行计算。求得三种工况下的模型应力与变形情况。

图3 有限元模型和板厚分布云图
3.2不同工况下的机舱总段吊装模拟计算
利用有限元软件动态模拟机舱10A吊装过程,选取模型的上升LC1、移位LC2、下降LC3三种工况下的不同姿态进行计算。
(1) LC1工况下模型模拟计算。
① 吊码载荷计算。
首先根据模型吊装上升阶段过程,随机选取17组时间点计算出吊码的载荷,分析不同区域吊码受力情况。具体负荷如图4所示。

图4 LC1工况下吊码的时间—载荷历程曲线
根据历程曲线分析可知:起吊上升阶段,第1组和第3组、第2组与第4组的吊码载荷变化基本一致,说明了对称区域内的吊码载荷历程曲线变化趋势基本一致。此工况下最大载荷发生在205 s时的第1组吊码上,此时最大载荷值为43.19503×104N,考虑到安全系数,吊码类型选择为Z-60,共4只承重168.5 t。在实际搭载过程中,分段吊装运动轨迹是由一个个断断续续的时间点构成。前30 s内没有控制好速度的变化,从而导致曲线的斜率较大。
② 结构变形与应力计算结果分析。
通过数值模拟计算,上升阶段总段结构响应情况如图5所示。
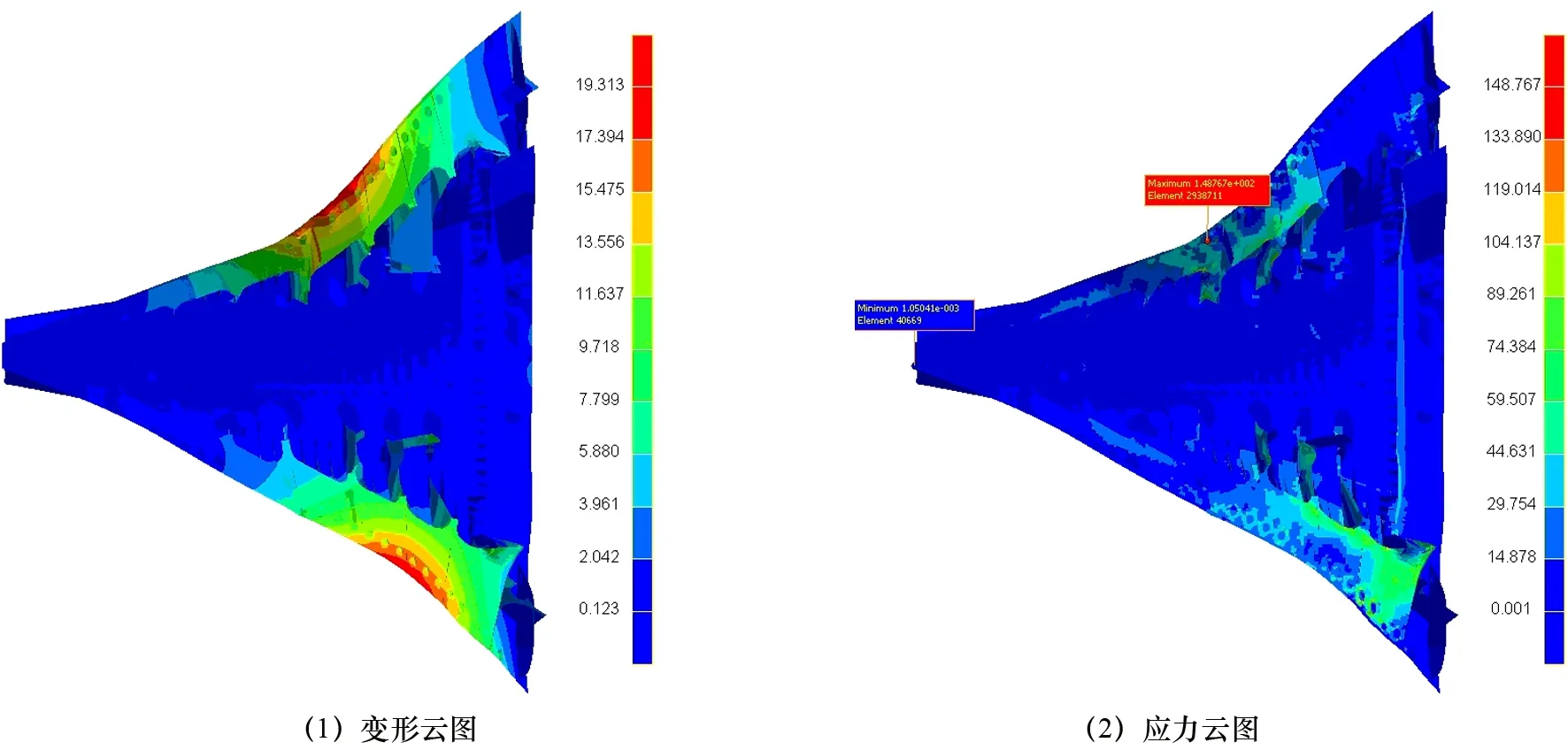
图5 LC1工况下机舱总段的应力和变形云图
根据计算结果分析可知:总段起吊阶段最大变形为19.31 mm,发生在42#肋位处的右舷结构边缘处,属于弹性变形,吊装结束可自行恢复。分段上升阶段板材的最大应力为148.77 MPa,发生于安装吊码的结构单元上。考虑1.5倍安全系数,结构许用应力为156 MPa,满足要求。
(2) LC2工况下模型模拟计算。
① 吊码载荷计算。
选取移位阶段若干组时间点,计算出对应吊码载荷数值,形成变化曲线,如图6所示。
第1、3组吊码随着时间推移而减小,而第2、4组吊码则恰好相反。这两组吊码载荷曲线走势证明了上升阶段得出的结论:对称区域内的吊码载荷历程曲线变化趋势基本一致,此结论是正确的。其中该阶段最大载荷为第2组区域的吊码,最大值为65.86 t,远大于其他组。这是由于第2组吊码在吊装移动方向上,吊装移位过程中总段发生轻微前倾,吊绳牵引力在Y方向分力较大,从而引起吊码载荷普遍高于其他区域吊码负荷。
在移位的前期,模型尚未处在平衡状态中,加速度较大,因此承受载荷较大。随着时间的推移达到平衡,数值缓慢地降下来,变化幅度减小。在实际的移位过程中,必须控制好前期的进度,不断根据吊钩的载荷变化幅度,控制好位移速度,从而控制载荷[5]。
② 结构变形与应力计算结果分析。
根据图7历程曲线可知:总段吊装运输阶段,结构最大变形、应力分布情况与吊装上升阶段基本一致。最大结构变形也是发生在42#肋位处的右舷结构边缘处,大小为24.45 mm,在弹性变形范围内,在外力消除后变形即消失。最大应力为185.46 MPa,考虑1.5倍的安全系数,应力值超出材料许用应力范围,需采取控制应力措施。
(3) LC3工况下模型模拟计算。
① 吊码载荷计算。
通过对四组吊码的载荷数值分析,形成各自区域的载荷历程曲线,如图8所示。

图6 LC2工况下吊码的时间—载荷历程曲线

图7 LC2工况下机舱总段的应力和变形云图
模型吊装的下降阶段,第1、3组的曲线走势相近,而第2、4组相差较大,两组数值起伏较大。下降阶段的载荷变化起伏较大,波谷值与波峰值之间最大相差达到24.25 t,这说明在模拟吊装过程中下降速度较快,没有掌控好速度,从而导致载荷波动较大。从该模拟结果得出吊装作业时必须控制好速度,使其达到匀速升降及移位。吊码最大载荷出现在635 s下的第2组吊码上,最大值为56.26 t,下降阶段内的应力势必也在不断变化,该区域结构强度要求较高,应给予重点关注。
② 结构变形与应力计算结果分析。
模拟计算吊装过程中下降阶段的某一时间点,得出结构变形和应力云图,结果如图9所示。

图8 LC3工况下吊码的时间—载荷历程曲线
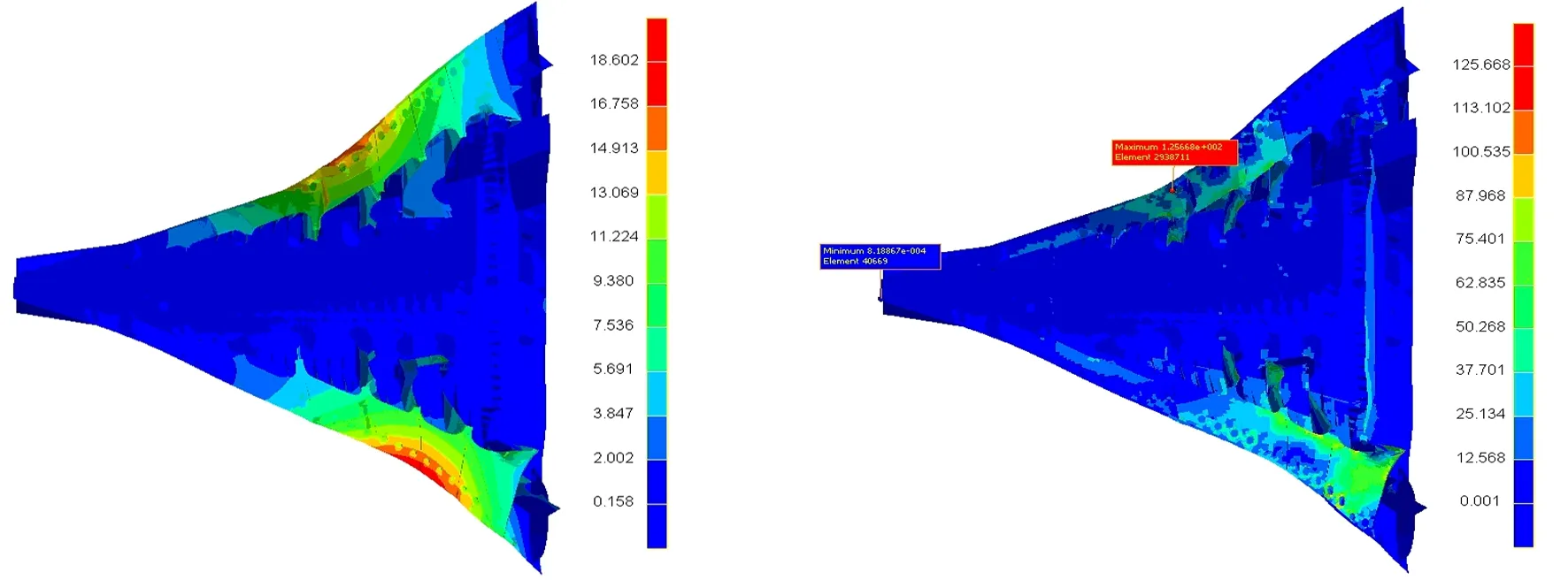
图9 LC3工况下吊码区域的最大变形、应力云图
对模拟计算结果分析可知:分段起吊阶段最大变形为18.60 mm,发生在42#肋位处的左、右舷结构边缘处,在弹性变形范围内,取消受力后结构可自行恢复。最大应力出现在布置第2组吊码的结构单元上,最大值为125.67 MPa,小于1.5倍下的许用应力156 MPa。
4结论
本文通过对10A机舱总段整个吊装过程进行强度有限元研究,根据本文计算结果的分析,可得到以下结论。
[][]
(1) 10A总段整个吊装3个阶段发生的结构变形、应力基本在允许范围内,满足生产要求;移位阶段的第2组吊码所在的42#肋位处的右舷结构应力值较大,超出许用应力,因此在该处应设置加强构件以达到足够的强度。
(2) 吊装时吊码安装位置的应力较大,吊码下方应有良好的支撑结构,如可以加厚吊码处的下围壁板,将有利于力的传导,从而减小吊装时结构的应力及变形。
(3) 对实际工作中选择吊码类型有指导性作用。分析整个吊装过程中不同区域吊码负荷变化情况,可知移位阶段吊码载荷均高于其他两个阶段,故在确定吊码类型时主要以移位阶段的吊码载荷为依据。初步吊码选型:第1组为Z-35T,第2组为Z-70T,第3组为Z-30T,第4组为Z-30T。然后再根据总段总重及各分段重量、实际生产经验确定吊码类型。
参考文献
[1]刘玉君, 汪骥.船舶建造工艺学[M].大连:大连理工出版社, 2011.
[2]Rajasekaran S, Annet D, Sang Choo Y. Optimal Locations for Heavy Lifts for Offshore Platforms [J]. Asian Journal of Civil Engineering, 2008(9):605-627.
[3]徐柏鑫,龙映玲,袁辉.9 400TEU集装箱船上层建筑整体吊装技术研究[J].船舶工程,2014(5):96-98.
[4]程玉芹.上船建造吊装工艺研究[D].镇江:江苏科技大学,2013.
[5]王锋,汪家政.大型船舶上层建筑整体吊装技术研究及应用[J].造船技术, 2011(1):20-22.
作者简介:刘锐(1989-),男,硕士研究生,从事船舶设计工作。
中图分类号U662
文献标志码A
Finite Element Analysis of Integral Lifting Strength of 208 000 DWT Bulk Carrier's Cabin
LIU Rui1, WANG Ming2,3, ZHANG Jian3, HE Wen-xin3
(1.Wuchang Ship Heavy Industry Group Co., Ltd., Wuhan Hubei 430060, China; 2.Shanghai Waigaoqiao Shipbuilding Co., Ltd., Shanghai 200137, China;3.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang Jiangsu 212003, China)
AbstractIntegral lifting is an important process in shipbuilding. Considering the requirements of the shipyard and complexity of the cabin section of the 208 000 DWT bulk carrier, structural response during integral lifting must be simulated by 3-D finite element method. Based on the study of the whole lifting process of the large bulk carrier's cabin, the load history curves of different regions are analyzed in this paper. Using finite element method, dynamic numerical simulation analysis is carried out on the lifting process in lifting rise, shifting carriage and decline in three different stages, then stress and deformation of the cabin in the process are obtained. The relevant results obtained by the finite element analysis can be used to select the type of hanging code, control the deformation of the structures and optimization of the integral lifting scheme of carrier's cabin.
KeywordsGeneral section of carbin Lifting strengthHanging code loadFinite element analysis

