基于地磁传感器与陀螺仪的姿态测量法*
闫爱天,陈 雄,周长省,邹晗霆
(南京理工大学,南京 210094)
基于地磁传感器与陀螺仪的姿态测量法*
闫爱天,陈雄,周长省,邹晗霆
(南京理工大学,南京210094)
摘要:姿态测量系统是火箭弹简易制导领域不可或缺的一部分。文中基于地磁传感器与MEMS陀螺仪的姿态测量系统,对传统单点姿态测量方法进行了研究与改进。以MEMS陀螺仪解算所得的偏航角作为三轴地磁传感器输入,推导了姿态角测量方法。针对姿态测量方法,设计了三轴地磁传感器姿态测量模块,在三轴旋转平台上进行了半实物仿真实验。实验结果表明,改进后的方法可以满足火箭弹姿态解算,提高了姿态角解算精度。
关键词:姿态测量;地磁传感器;MEMS陀螺仪;半实物仿真
0引言
弹丸飞行姿态的获取对弹丸的设计及研究具有重要的意义。目前弹丸飞行过程姿态测量方法主要有GPS、太阳方位角法、加速度计法、光电测量法等。这些方法有的成本较高、有的精度不够,都限制了自身在制导领域的应用。随着微电子技术的发展和新型地磁传感器的出现,地磁探测技术取得很大的进步和提高,其在军事上的发展和应用也得到关注和研究。基于地磁传感器与MEMS陀螺仪的简易制导修正引信具有全天候、全地域、简易高效、性能稳定、抗冲击和过载能力强等特点,使其非常适合简易制导的应用[1]。同时地磁与MEMS陀螺相结合的姿态测量技术可解决地磁姿态测量不能独立求解的问题,可以大限度降低MEMS陀螺精度不足造成的影响。通过相关算法实现对弹丸飞行姿态角的实时测量,使得简易制导弹药能够根据其姿态信息实时对飞行弹道进行修正,实现精确打击[2]。但传统姿态测量方法或者未判别姿态角单值解[3],或者将俯仰角、滚转角作为地磁传感器输入从而造成较大误差[4],影响了姿态测量系统的精度。
文中对基于两轴陀螺仪与三轴地磁传感器姿态角测量方法进行了研究,通过两轴陀螺仪对偏航角进行解算,降低了解算俯仰角或以弹道偏角代替偏航角进行解算所造成较大误差。最后通过仿真结果对姿态角误差进行了分析,仿真结果表明较传统方法姿态角误差明显减小。
1姿态测量系统描述
地磁姿态角测量技术不能独立解算全部3个姿态角,必须已知至少一个姿态角才能解算另外两个姿态角,因此基于地磁传感器与MEMS陀螺仪的传统姿态测量方法主要通过MEMS陀螺仪得到一个姿态角,将所得姿态角作为磁阻传感器输入从而解算得到剩余两个姿态角。
基于三轴地磁传感器与MEMS陀螺仪的姿态测量系统整体架构图如图1所示,主要由C8051F系列单片机、三轴地磁传感器、两轴MEMS陀螺仪、E2PROM存储模块、上位机构成。系统首先利用MEMS陀螺仪测得偏航角速率,通过积分得到偏航角。其次利用三轴地磁传感器测得3个敏感轴方向的地磁矢量大小。最后将所得偏航角与三轴地磁传感器所测得3个地磁矢量大小传输给上位机,利用文中推导的姿态测量方法进行姿态角的解算,从而得到剩余姿态角,实现姿态角完全解算。
2传感器安装
描述弹丸运动涉及多个坐标系。其中OXtYtZt
为地理坐标系,三轴分别指向东北天,即:Xt指向地球表面切平面且指向东方,Yt轴指向北,Zt轴指向天。OXbYbZb为弹体坐标系(见图2),三轴方向分别为:Yb轴沿着弹体旋转轴指向运动方向,Xb轴和Zb轴沿弹体径向分别指向右、上。地磁传感器敏感轴分别沿着坐标系OXbYbZb三轴方向,陀螺仪两轴分别沿着OXb、OZb方向[5]。弹体坐标系下3个敏感轴的角速率记为ωbx、ωby、ωbz。由地理坐标系OXtYtZt到弹体坐标系OXbYbZb转换的3个欧拉角γ、θ、φ(γ为滚转角,θ为俯仰角,φ为偏航角)。

图2 弹体坐标系与姿态角
在简易制导应用中,通常利用GPS模块提供的弹丸在地理坐标系下的速度信息,求得弹丸在地理坐标系下的弹道偏角φ,一般认为偏航角φ为弹道偏角φ与射向角ψ的差值,从而可得转换矩阵[6]为:
(1)
3姿态测量算法研究
地磁矢量H在地理坐标系OXtYtZt上的投影分量分别为Hx、Hy、Hz,在弹体坐标系OXbYbZb上的投影分量分别为Hbx、Hby、Hbz,地磁矢量在两个坐标系分量之间的关系[3]为:
(2)
陀螺仪角速度矢量在两个坐标系之间的关系为:
(3)
式(2)无法提供独立的3个方程进行姿态解算,须利用陀螺仪给予一个姿态角输入,当利用陀螺仪得到偏航角,根据式(2)可以得到俯仰角θ与滚转角γ的表达式:
(4)
其中γ、θ、φ的取值范围分别为[0,2π)、(-π/2,π/2)、(-π,π]。对于式(4)正负号的选取用表1表示。
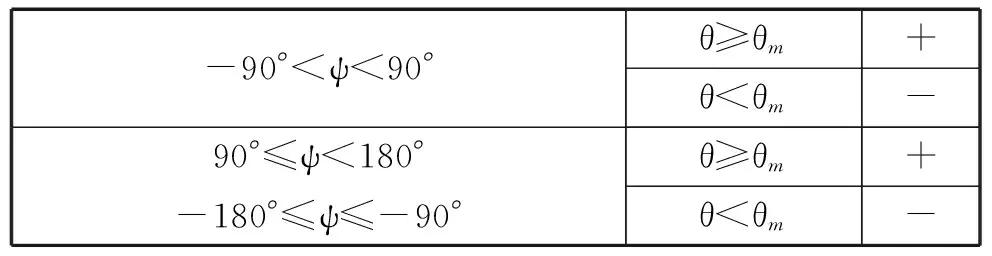
表1 地磁测量方程正负号选取表
其中,ψ为射向角,θ为俯仰角,θm为地磁俯仰角。
(5)
简易制导火箭弹发射为非垂直发射,由式(3)可得非垂直发射时关于偏航角与俯仰角的积分式分别为:
(6)
(7)
简易制导火箭弹飞行过程姿态角中,偏航角变化较小,因此时间积累引起的累计误差小,利用双轴陀螺仪为地磁传感器提供偏航角信息进行姿态解算的精度相对较高,偏航角积分方程为:
(8)
利用两轴MEMS陀螺仪每周期采集角速度信息,结合地磁传感器提供的另外两个姿态角,基于龙格库塔法综合式(4)、式(8)进行姿态角求解,具体步骤为:
1)P1=C(t)ωby(t)-S(t)ωbz(t);
2)P2=C(t)ωby(t+T/2)-S(t)ωbz(t+T/2)+
P1/2;
3)P3=C(t)ωby(t+T/2)-S(t)ωbz(t+T/2)+
P2/2;
4)P4=C(t)ωby(t+T)-S(t)ωbz(t+T)+P3;
5)P=(P1+2P2+2P3+P4)/2;
6)φ(t+T)=φ(t)+(T/6)P。
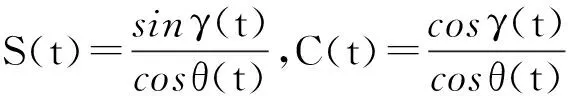
4半实物仿真实验
在理论算法研究的基础上,利用Honeywell公司的HMC1043三轴地磁传感器和C8051F310单片机设计了地磁姿态测量模块,硬件电路见图3,该硬件模块可实现以下功能:1)三轴地磁信号的测量;2)三轴地磁信号的采集与存储;3)与上位机进行数据通信。为了验证与考察算法的可行性与精度,针对前文推导的基于地磁传感器与MEMS陀螺仪姿态测量算法,设计了姿态测量算法的仿真实验。将地磁姿态测量模块安装在三轴旋转平台上,使得地磁传感器敏感轴与三轴平台转轴方向重合。

图3 地磁姿态测量模块
在不考虑陀螺仪误差的条件下,具体步骤如下:
1)以一种火箭弹为实例,利用Matlab建立六自由度外弹道方程程序。
2)通过弹道仿真得到弹体坐标系下角速度(分别得到俯仰角速率、偏航角速率)序列{ωθi}{ωφi},将定方差随机数序列生成的白噪声加至角速度序列并作为MEMS陀螺仪输出。
3)分别对角速率序列{ωθi}{ωφi}进行积分计算,得到俯仰角序列{θi}、偏航角序列{φi}。
4)转台以10r/s的速度匀速转动100s(系统作滚转运动)的同时,输入角相对应轴作来回摆动,地磁信号存储于地磁模块E2PROM中(地磁模块已预校正)。
5)将俯仰角序列{θi}、偏航角序列{φi}与地磁信号传送给上位机,上位机利用基于方程(4)的姿态测量程序进行剩余两个姿态角的计算。
三轴地磁传感器的输出电压曲线如图4。分别由俯仰角速率序列与偏航角速率序列积分得到俯仰角序列与偏航角序列,根据已知姿态角序列计算剩余两个姿态角,分别用以俯仰角序列、偏航角序列用两种方法解算滚转角和转台输出的滚转角作差,得到滚转角误差如图5(图5(a)是以俯仰角作为输入角时的滚转角误差,图5(b)是以偏航角作为输入角时的滚转角误差)。由图5可看出,以偏航角作为地磁模块输入所得到的滚转角误差明显小于以俯仰角作为输入所得滚转角误差。其中以俯仰角作为地磁模块输入的解算方法所得滚转角误差方差为0.1°,以偏航角作为地磁模块输入的解算方法所得滚转角误差的方差为0.05°。
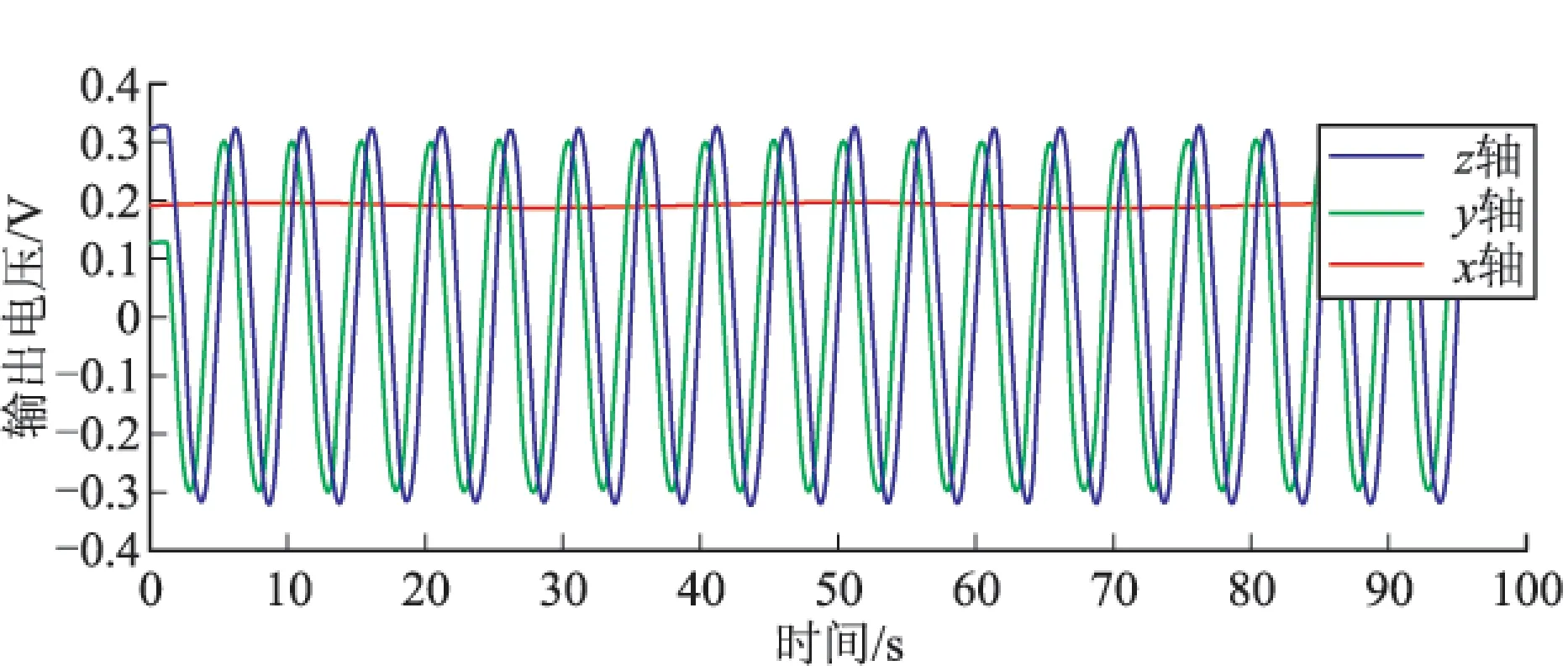
图4 三轴地磁传感器输出
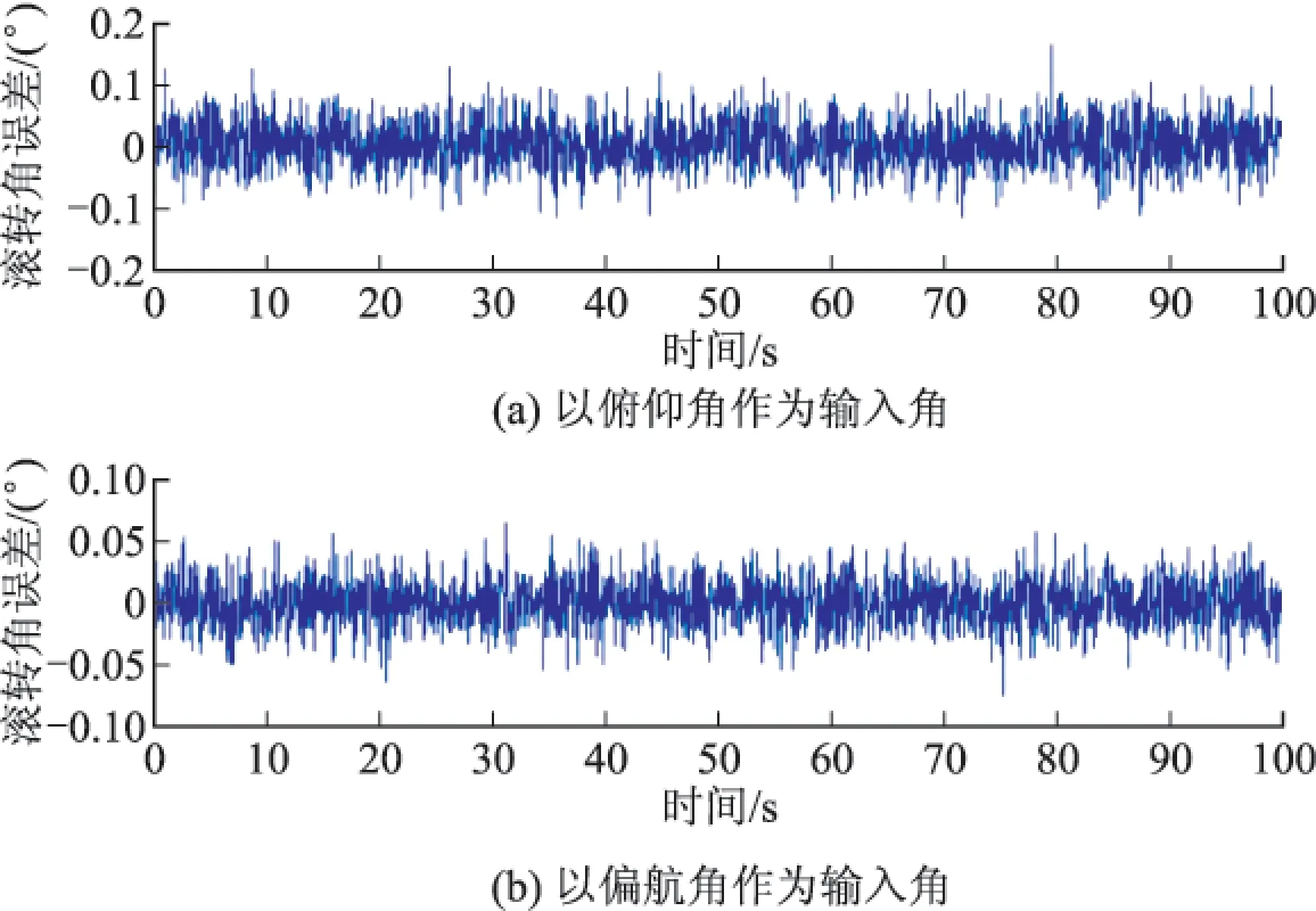
图5 不同输入角时滚转角误差曲线图
5结论
1)文中研究了基于三轴地磁传感器与MEMS陀螺仪姿态测量系统的姿态角解算方法。以偏航角作为地磁模块输入角,推导了3个姿态角的解算公式。
针对解算方法设计了三轴地磁传感器姿态测量模块,进行了半实物仿真实验。
2)由仿真结果可知,改进后的姿态测量方法,满足一定的测量精度要求。弹丸在飞行状态进行姿态角解算不会出现超出陀螺量程的问题,同时对比传统以俯仰角作为地磁传感器输入的姿态测量方法,改进后的方法使得解算后姿态角误差明显减小。
参考文献:
[1]龙礼, 张合, 唐玉发, 等. 自适应卡尔曼滤波在地磁姿态检测中的应用 [J]. 兵工学报, 2013, 34(9): 1155-1160.
[2]刘建敬, 张合, 丁立波, 等. 地磁信息感应装定系统及其插值算法 [J]. 中国惯性技术学报, 2011, 19(6): 692-695.
[3]曹红松, 冯顺山, 赵捍东, 等. 地磁陀螺组合弹药姿态探测技术研究 [J]. 弹箭与制导学报, 2006, 26(3): 142-145.
[4]代钢, 李枚, 苏伟, 等. 自旋导弹捷联式陀螺/地磁姿态测量方法 [J]. 中国惯性技术学报, 2010, 18(6): 702-705.
[5]钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2012: 31-35.
[6]XIANGChao,BUXiongzhu,YANGBo.Threedifferentattitudemeasurementsofspinningprojectilebasedonmagneticsensors[J].Measurement, 2014, 47: 331-340.
*收稿日期:2015-01-29
基金项目:南京理工大学自主科研专项计划项目(ZDJH02)资助
作者简介:闫爱天(1990-),男,江苏南京人,硕士研究生,研究方向:制导与控制。
中图分类号:V249.12
文献标志码:A
AttitudeMeasurementBasedonMagnetometerandMEMSGyroscope
YANAitian,CHENXiong,ZHOUChangsheng,ZOUHanting
(NanjingUniversityofScienceandTechnology,Nanjing210094,China)
Abstract:Attitude measurement system is an indispensable part of rocket simple guidance field. Based on magnetometer and MEMS gyroscope, traditional single-point attitude measuring method was studied and improved. Yaw angle solved by MEMS gyroscope was taken as input of three-axis magnetometer for measuring attitude angle. In view of the attitude measurement method, a three-axis magnetometer measuring system was designed and semi-physical simulation experiments were carried out on three-axis rotation platform. The results show that the improved method can satisfy missile attitude algorithm and the precision is improved.
Keywords:attitude measurement; magnetometer; MEMS gyroscope; semi-physical simulation

