二维弹道修正引信制动控制建模与仿真*
卢志才,高 敏,贾春宁
(1 解放军军械工程学院,石家庄 050003;2 总装驻上海地区军事代表室,上海 201109)
二维弹道修正引信制动控制建模与仿真*
卢志才1,高敏1,贾春宁2
(1解放军军械工程学院,石家庄050003;2总装驻上海地区军事代表室,上海201109)
摘要:为解决二维弹道修正引信滚转姿态实时控制问题,提出了固定舵制动模型。根据弹道修正原理及固定舵控制规律,建立了制动控制数学模型。构建了基于双轴仿真测试转台的半实物仿真系统,对不同弹道环境下制动控制性能进行了半实物仿真。结果表明干扰力矩在0~0.5 N·m变化范围,该方法能够有效跟踪滚转角控制指令实现实时跟踪。当弹丸转速在100~167 r/s范围时,该模型制动时间和精度满足控制系统总体要求。
关键词:固定舵;半实物仿真;制动控制;直流电机;二维弹道修正引信
0引言
二维弹道修正引信通过卫星导航接收机测量弹丸速度、位置信息,以固定鸭舵作为执行机构,当弹丸存在弹道偏差时,按照导引规律将固定舵制动在某一滚转角度,对弹道偏差进行修正。其中,固定舵执行机构可以采用直流电机[1-2]。
Wernert P和Theodoulis S研究了弹道修正引信(CCF),引信头部有两对控制舵面,分别实现俯仰和偏航方向的控制,同时两对舵面可实现引信修正组件的减旋[3]。Wernert P介绍了采用一对固定舵面用于减旋,一对操纵舵面用于二维修正的引信设计方案,并依据Costello M的线性化理论对该型号弹丸的稳定性进行了分析[4]。国内也在开展二维弹道修正引信方案的研究,霍鹏飞、李东光等研究了155 mm二维弹道修正引信总体技术,对弹道方案、制导控制方案以及分系统方案进行了深入研究[5-6]。
为了满足不同空气导转力矩作用条件下固定舵实时控制的需求,文中提出了制动控制模型,并对其进行了数字和半实物仿真。该制动模型采用增量PID控制算法,通过速度环/位置环实现了固定舵的滚转角控制,半实物仿真系统能够对固定舵在不同转速、不同控制角度下控制性能进行充分验证,为考核边界条件下固定舵制动控制性能提供参考途径。以某型弹道修正弹为例,对其不同飞行速度下的固定舵导转力矩进行了分析,以此为输入条件对制动控制模型进行了验证,并给出了相应的结果和分析。
1固定舵运动学模型
二维弹道修正引信是由在引信体上增加两组舵面,舵偏角为固定的,可称为固定舵,如图1所示。

图1 二维弹道修正引信外形图
其中,一对同向舵面(舵面2、舵面4)提供弹道偏差所需的气动力,一组差动舵面(舵面1、舵面3)提供空气导转力矩。配装二维弹道修正引信的155 mm榴弹总体布局如图2所示。

图2 配装有二维弹道修正引信的155 mm榴弹
固定舵导转力矩与差动舵面翼展、安装角以及飞行速度有关,翼展和安装角确定后,导转力矩与弹丸飞行速度成正比关系。对不同飞行速度下155 mm弹道修正榴弹空气导转力矩进行了计算,结果如图3所示。可知155 mm榴弹飞行速度在0.5~2Ma范围内变化时,固定舵导转力矩在0.1~3.3 N·m范围内变化。

图3 导转力矩与飞行速度关系图
二维弹道修正引信应用对象为右旋榴弹,出炮口至弹丸落地,弹丸运动可分为3个阶段:第一阶段在炮膛内存在着强大的轴向过载,舵面跟随弹丸向右旋转;第二阶段出炮口后,舵面在较短时间内向右转速减小,并形成向左转动,直至达到向左的平衡转速;第三阶段弹道修正阶段,通过调节制动力矩将固定舵制动在发射惯性系下需要的滚转角度。
1.1固定舵减旋过程
弹丸出炮口后,固定舵减小右旋速度,此时舵面导转力矩Mx方向向左,同时空气极阻尼力矩Mxz也向左,而制动力矩Me1和轴承摩擦力矩Mg向右,满足式(1)的条件。
(1)
该过程中弹丸飞行速度较快,导转力矩Mx较大,制动力矩Me1为电机最小力矩。
1.2固定舵平衡转速状态
固定舵转速经过减旋,逐渐向左转动,并达到左向平衡转速。此时舵面导转力矩Mx方向向左,空气极阻尼力矩Mxz向右,而制动力矩Me1和轴承摩擦力矩Mg向右,只要满足式(2)的条件即可。
(2)
此时,制动力矩Me1为电机最小力矩,轴承摩擦力矩Mg较小,极阻尼力矩Mxz与转速和马赫数有关,舵面导转力矩Mx与马赫数有关,达到平衡转速时,式(2)成立。
1.3修正过程的力矩要求
在修正过程中,通过增大制动力矩将左旋的固定舵制动在所需的滚转角度,此时需要满足式(3),由于此时转速接近于0,基本可以不考虑空气极阻尼力矩Mxz。
(3)
式中:Me2为制动固定舵所需的电磁力矩,其大小随固定舵导转力矩不同而变化。二维弹道修正引信采用直流电机,电枢电压为Ua,转速为ω,扰动力矩为Tc,由电机特性可得:
(4)
通过调节电机负载对制动力矩进行控制,进而达到对固定舵旋转速度和角度的控制。
配装有二维弹道修正引信榴弹在飞行过程中采用闭环控制,根据弹道纵向、横向偏差,形成滚转控制指令,制动模块根据此滚转指令对固定舵滚转进行伺服控制,最终使固定舵的滚转姿态角相对发射惯性坐标系静止,实现对弹丸弹道偏差的修正。
2制动控制算法建模与仿真
2.1制动控制算法
根据二维弹道修正引信的修正原理,修正引信系统主要由卫星导航接收机、磁传感器、直流电机、弹载计算机、装定、电源等模块构成,如图4所示。
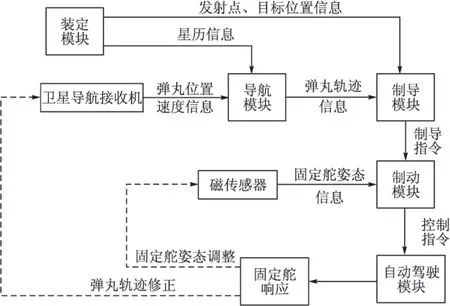
图4 系统原理框图
导航模块、制导模块和控制模块均为弹载计算机包含的功能模块,发射前进行控制参数和卫星星历装定,弹丸发射后,卫星导航接收机开始接收卫星信号,并输出弹丸位置、速度等信息,经过导航模块的处理形成弹丸轨迹信息;制导模块根据弹丸轨迹信息和目标点位置信息,利用制导律形成制导指令并传递到控制模块;控制模块根据制导指令和实测引信滚转姿态信息形成控制指令;固定舵在控制指令的作用下调整其滚转姿态;引信姿态的调整将反映在磁传感器的测量信号上,该测量信号进入控制模块,形成引信姿态调整回路;引信姿态的变化影响弹丸飞行轨迹,进而反映在弹道测量结果中,该测量结果继续输入导航模块,形成弹道修正回路。
固定舵闭环控制方案如图5所示,其输入是弹道解算生成的指令角度γzi,其输出是固定舵实际的滚转角γz。

图5 弹道修正控制工作原理
执行机构为直流电机,利用控制器的高分辨率PWM,控制MOSFET,调整电机的负载,当电机负载量增大时外转子转速将减小,当负载量减小时外转子的转速将增加,利用此原理实现操纵舵片的转速控制。当固定舵旋转速度在发射坐标系下接近0时,调整操纵固定舵的滚转角度值,实现固定舵的位置控制。
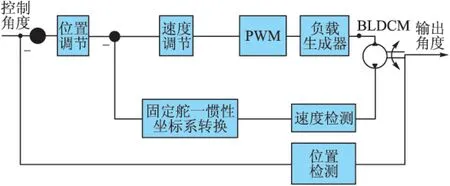
图6 固定舵闭环伺服控制方案
采用基于速率环/位置环的串级控制方案,在控制算法上则采用增量式PID控制算法实现快速跟踪和滚转角的高精度定位。
控制器测量的外转子的转速和滚转角,利用增量式PID控制算法,通过高精度PWM输出控制直流电机负载,当固定舵旋转速度接近0时,再根据设置的滚转角度值和当前实际滚转角度值比较,利用PID算法使当前滚转角度和设置的滚转角度一致。自适应PID控制算法的计算公式如下:
(5)
式中:kp为比例系数;ki为积分时间常数;kd为微分时间常数。
2.2数学仿真分析
为验证二维弹道修正引信制动控制算法的有效性,采用Matlab/Simulink对算法进行建模,二维弹道修正引信制动控制仿真模型如图7所示。
仿真过程中,电机参数为:定子相绕电阻R=3 Ω,定子相绕组自感L=0.04 H,互感L=-0.07 H,转动惯量J=0.06 kg·m2,12 V直流电源供电。制动指令角度采用脉冲串,固定舵导转力矩采用幅值为3 N·m的正弦波,直流电机采用PWM控制方式,Simulink求解器步长设置为变步长,采用ode23,仿真时间为2.5 s。
滚转控制角度采用脉冲串,控制角度分别为10°、0°,脉冲串频率为2 Hz;为验证不同干扰力矩作用固定舵的制动效果,干扰力矩Tq采用幅值为0.5 N·m的正弦波;直流电机电压为12 V,通过滚转控制角度和固定舵滚转输出角度之差形成PWM控制,PWM占空比正比于控制角与输出角之差。
利用增量式PID控制算法,制动控制指令与固定舵输出的滚转角度如图8所示。
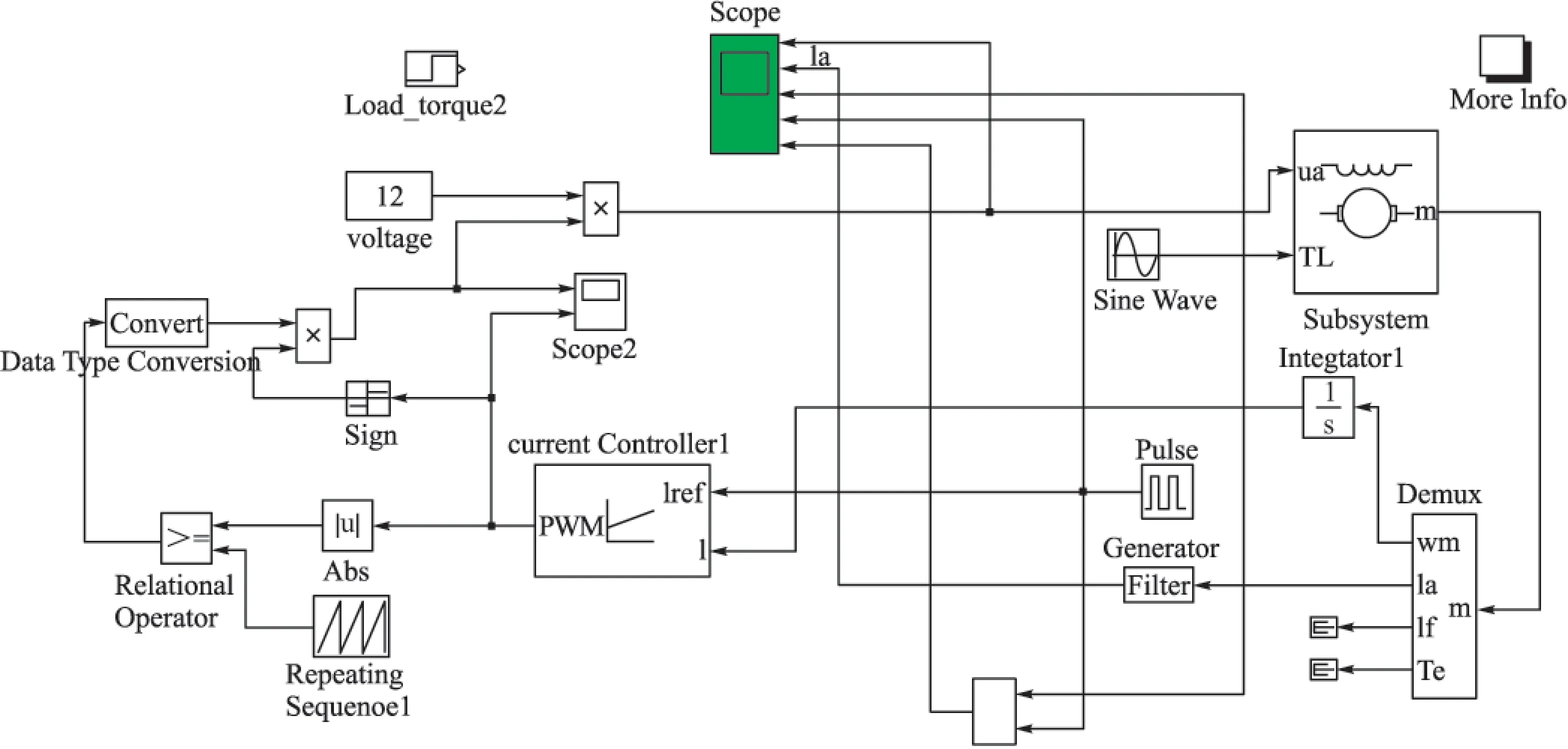
图7 二维弹道修正引信制动控制仿真模型

图8 制动系统控制角度与输出对比图
由图8仿真结果可知,当固定舵空气导转力矩在-1.5~1.5 N·m范围变化时,直流电机可以将固定舵制动到所需滚转角度,制动系统响应快速平稳,超调量较小,满足固定舵弹道修正对制动角度的要求。
3制动控制半实物仿真试验
为验证制动控制系统在不同转速、不同制动角度、不同导转力矩作用时的控制效果,设计了双轴仿真测试转台,分别利用电机带动固定舵和弹丸旋转,仿真飞行过程中弹体与引信部可以相对地面坐标系反向旋转。双轴仿真测试台如图9所示。

图9 双轴仿真测试台
3.1弹丸不同转速下制动控制试验
固定舵弹道修正前,在发射惯性坐标系下弹丸与固定舵反向旋转,为验证弹丸在不同转速下固定舵制动效果,利用电机带动弹丸分别以6 000 r/min、7 000 r/min、8 000 r/min、9 000 r/min向右旋转(从弹尾方向看),固定舵在0.8 N·m导转力矩作用下向左旋转(从弹尾方向看),约20 s开始进行制动控制,不同转速下固定舵滚转角制动控制如图10所示。
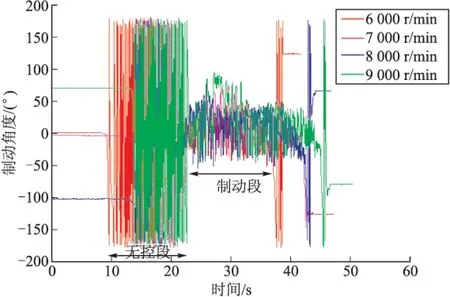
图10 不同转速下滚转角控制结果
图10中当弹丸转速在6 000~9 000 r/min范围变化时,固定舵可以控制在0°滚转角附近,控制持续时间大于15 s。
3.2弹丸不同滚转角下制动控制试验
为仿真验证弹丸在不同控制滚转角制动效果,在弹丸转速为10 000 r/min时,滚转控制角分别0°、90°、180°、-90°,弹载地磁组件采集固定舵滚转角,固定舵闭环控制结果如图11~图14所示,图中横坐标为采样点数,采样速率为100 Hz,纵坐标为固定舵滚转角,滚转角持续采样,截取制动过程滚转角采集数据。
图11中制动控制指令发出以后,固定舵滚转角速率首先降至0,约1.5 s开始将固定舵制动到0°,随着时间推移制动效果逐渐变差,制动时间可保持约95 s。
图12中截取的数据中,约3 s开始将固定舵制动到90°,制动时间可保持约52 s。
图13中截取的数据中,固定舵制动滚转角在180°和-180°之间跳变,这是由于弹载地磁组件定义滚转角变化为-180°~180°,固定舵制动时间可保持约36 s。
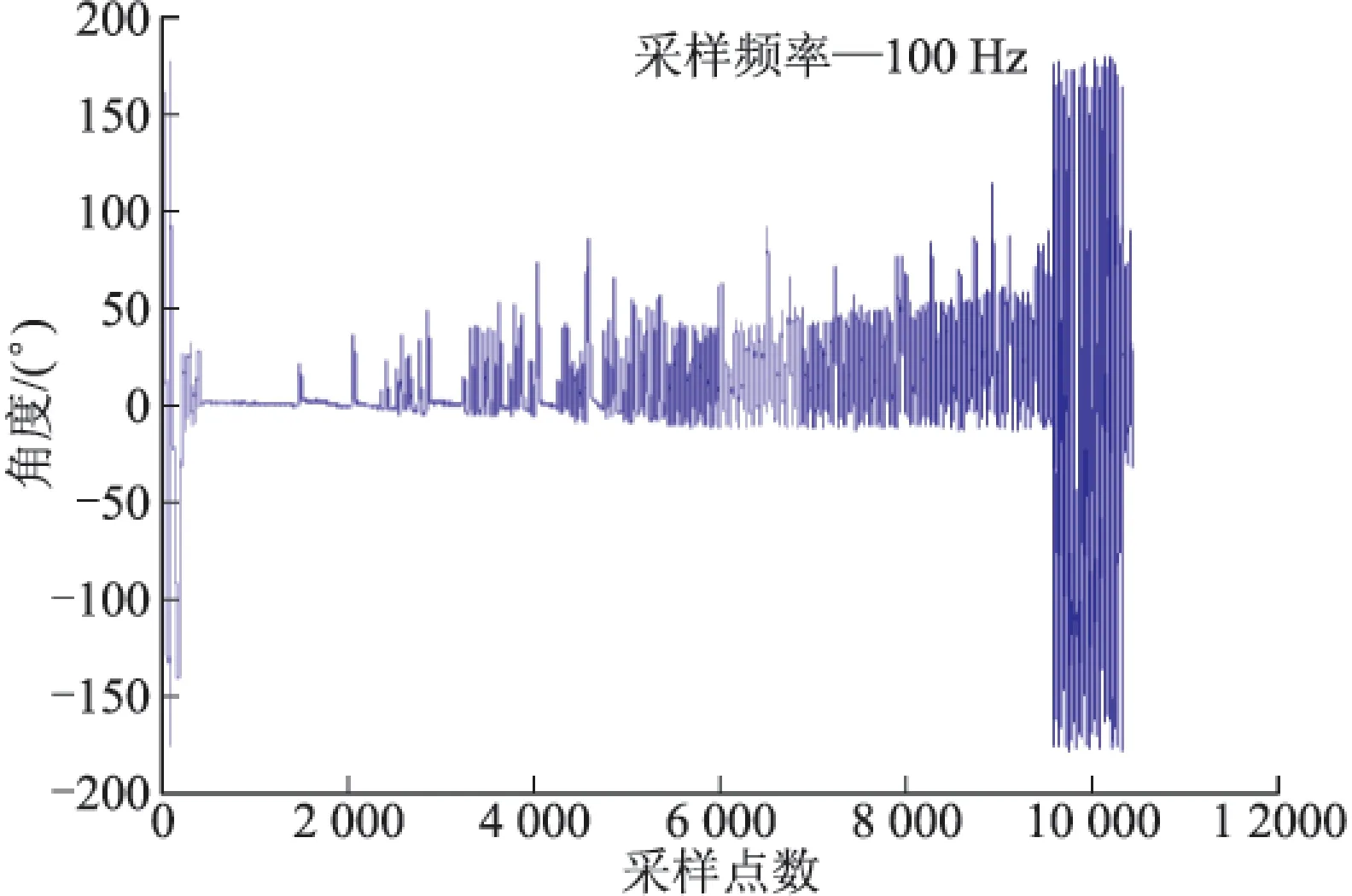
图11 控制角0°时固定舵滚转角
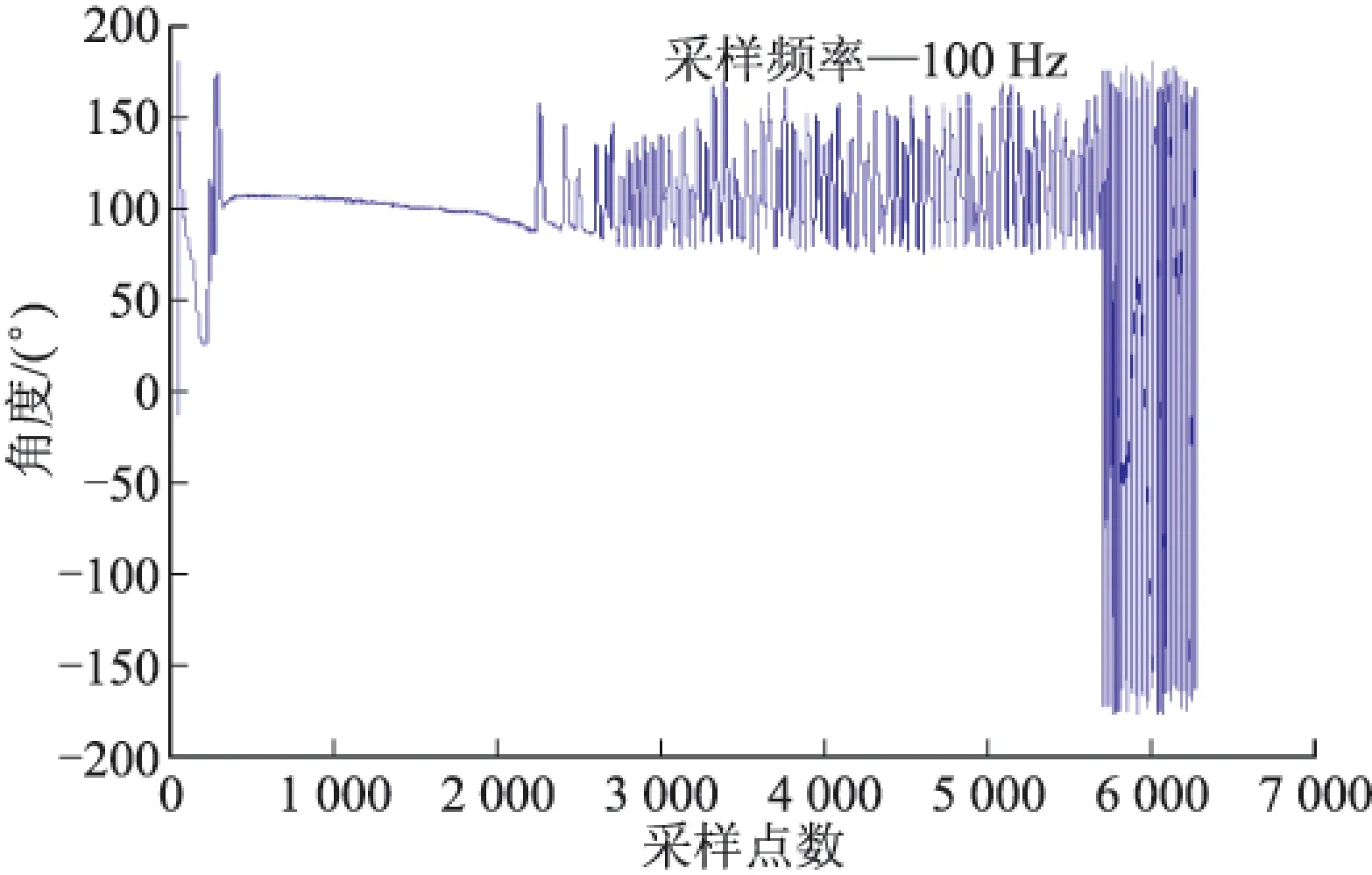
图12 控制角90°固定舵滚转角
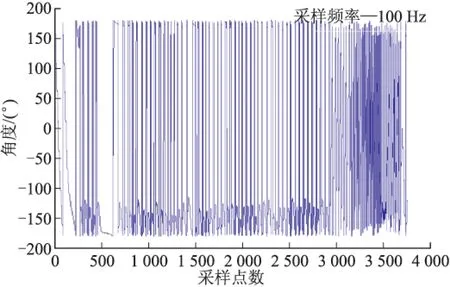
图13 控制角180°固定舵滚转角
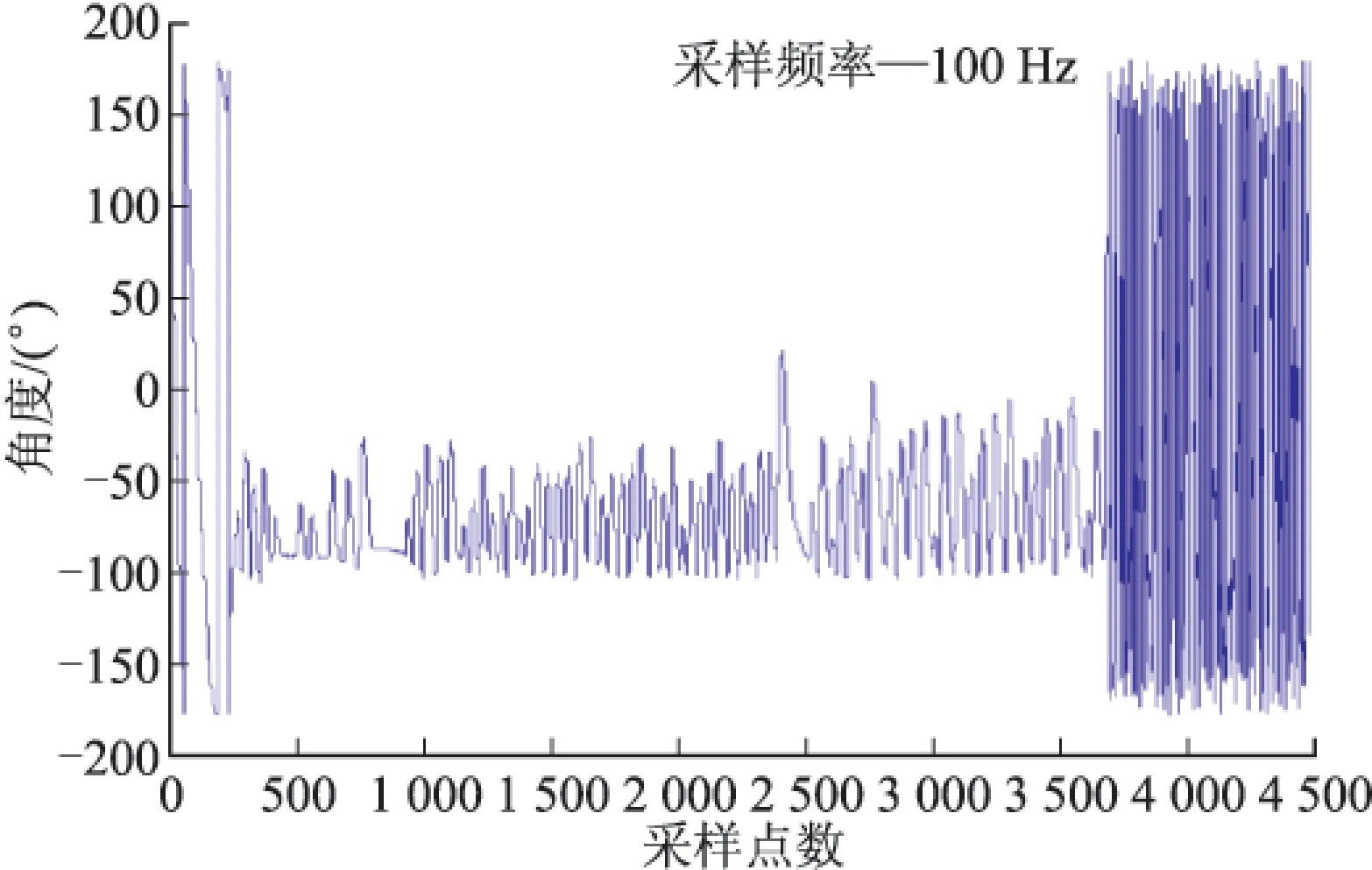
图14 控制角-90°固定舵滚转角
图14中固定舵制动时间可保持约34 s。
3.3试验结果分析与讨论
二维弹道修正引信在制动过程中,制动段滚转角速率和滚转角采集数据曲线都存在着较大跳动和误差,图11~图14中固定舵制动持续时间逐渐变短。对存在的两个问题进行了分析:
1)双轴仿真测试台在高速旋转时振动较大,振动对弹载地磁组件带来了干扰,使得地磁组件输出存在着抖动,如何消除双轴仿真测试台高速旋转带来的抖动是下一步半实物仿真工作中重要的研究内容;
2)二维弹道修正引信工作过程中,弹丸与引信部之间通过轴承进行连接,长时间工作后轴承产生大量的热,使得轴承摩擦力矩增大,导致制动持续时间逐渐变短。
4结束语
以制动技术为基础的二维弹道修正引信技术,能有效对固定舵进行滚转角控制,通过数字仿真和半实物仿真证明了固定舵制动控制模型能够在不同干扰力矩情况下将固定舵制动在所需的滚转角度,制动控制时间大于30 s,控制精度能够满足系统要求。进一步的工作是需要将制动控制算法在硬件上与制导控制算法进行集成。
参考文献:
[1]THEODOULIS Spilios, WERNERT Philippe. Flight Control for a Class of 155 mm Spin-stabilized Projectiles with Course Correction Fuse (CCF): AIAA 2011-6247 [R]. Portlond Oregon: AIAA, 2011.
[2]BURKE Peter J, PERGOLIZZI Anthony. XM1156 Precision Guidance Kit (PGK) Overview [C]∥2010 Fuze Conference, 2010.
[3]WERNERT Philippe. Stability analysis for canard guided dual-spin stabilized projectiles [C]∥ AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2009: 2-4.
[4]WERNERT Philippe, LEOPOLD Friedrich, BIDINO Denis. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile [C]∥ Honolulu Hawail AIAA Atmospheric Flight Mechanics and Exhibit, 2008: 2-4.
[5]高铭泽, 施坤林, 霍鹏飞. 引信滚转角双闭环控制算法 [J]. 探测与控制学报, 2013, 35(3): 16-18.
[6]纪秀玲, 王海鹏, 曾时明. 可旋转鸭舵对旋转弹丸纵向气动特性的影响 [J]. 北京理工大学学报, 2011, 31(3): 265-268.
*收稿日期:2015-03-3
基金项目:武器装备预研基金;军械工程学院基金(YJJXM13020)资助
作者简介:卢志才(1982-),男,河北深州人,讲师,博士,研究方向:弹箭制导技术。
中图分类号:TP242
文献标志码:A
Braking Control Model and Simulation for Precision Guided Kit
LU Zhicai1,GAO Min1,JIA Chunning2
(1Ordnance Engineering College of PLA, Shijiazhuang 050003, China;2Military Representative Office of General Armaments Department in Shanghai Area, Shanghai 201109, China)
Abstract:To solve roll attitude real-time control problem for a 155 mm canard guided dual-spin stabilized projectiles, braking control model was proposed. According to trajectory correction theory and canards braking principle, the trajectory braking control model was given. The semi-physical simulation system was set up based on tow-axis flight simulation table, which can drive the dual-spin stabilized projectiles at different roll rate. The results show that braking model can rack roll attitude control-instruction under condition of 0.5 N·m disturb moment, and the nose portion can brake accurately at control roll attitude when the projectiles rotate at 100 r/s to 167 r/s. The braking precision and duration time can fulfill the need of guidance and control system.
Keywords:fixed canards; semi-physical simulation; braking control; precision guided kit

