支持向量机多项式光滑函数的误差理论研究

何文斌　刘群锋　熊金志

(东莞理工学院计算机学院　广东东莞　523808)



支持向量机多项式光滑函数的误差理论研究

何文斌刘群锋熊金志

(东莞理工学院计算机学院广东东莞523808)

(hewb@dgut.edu.cn)

摘要光滑函数在光滑支持向量机的理论中起着重要作用.1996年Chen等人提出一个支持向量机的光滑函数——Sigmoid函数的积分函数，并解决了该光滑函数的误差问题.2005～2009年，袁玉波、熊金志和刘叶青等人相继提出支持向量机的无穷多个多项式光滑函数和多项式光滑的支持向量机模型，但都未解决这类多项式光滑函数的误差函数问题.为此，用 Newton-Hermite 插值方法研究该问题.研究结果表明：1)用 Newton-Hermite 插值方法可计算这类光滑函数的误差函数，并给出了具体算法；2)这类误差函数有无穷多个，可用一个一般形式表示，并得到了这个一般形式；3)这类误差函数具有许多重要性质，并给出了严格证明.解决了支持向量机无穷多个多项式光滑函数的误差函数及其性质问题，建立了这类多项式光滑函数的误差理论，为研究支持向量机的光滑理论提供了基本的理论支持.

关键词支持向量机；Newton-Hermite插值；光滑函数；误差函数；多项式

支持向量机是在统计学习理论的基础上发展起来的一种机器学习方法、是数据挖掘的一种新方法，广泛用于分类问题和回归问题，特别在文本分类、图像检索、人脸识别、语音识别、手写数字识别等领域有大量应用[1-4].但随着信息技术的迅猛发展，数据规模越来越大，其分类速度慢的问题日益突出.为此，在支持向量机理论的研究上，近年来出现了一个新的研究方向——光滑的支持向量机.这种光滑的支持向量机采用快速的求解算法，因而可以降低支持向量机的计算复杂性.该研究方向可分为光滑支持向量机模型和光滑函数2个方面.

在光滑支持向量机模型的研究方面，2001年，Lee等人[5]用Sigmoid函数的积分函数作为光滑函数，提出光滑的支持向量机模型；2005年，袁玉波、严杰和徐成贤[6]用多项式函数作为光滑函数，提出一个多项式光滑的支持向量机模型；同年Lee等人[7]用Sigmoid函数的积分函数的复合函数作为光滑函数，提出一个光滑的支持向量回归机模型；2008年，我们用一类多项式光滑函数，提出多项式光滑的支持向量机在分类问题中的一般模型[8]，还提出多项式光滑的支持向量回归机模型[9]；2009年，刘叶青等人[10]也提出多项式光滑的支持向量机.上述这些光滑模型因为可以采用快速的Newton-Armijo算法进行求解，所以可以提高分类速度或回归速度.但这种光滑模型都必须用适当的光滑函数对原支持向量机模型进行光滑处理才能得到.可见光滑函数是研究光滑支持向量机的前提和基础，研究光滑函数具有重要的理论意义.光滑支持向量机以往的研究主要是针对光滑函数的应用，例如对光滑支持向量机的模型及其性能、效率的研究，而对光滑函数自身性质的研究却很少见到.

在光滑函数的研究方面，1996年，Chen等人[11-12]针对数学规划问题中正号函数x+=max(0,x)不光滑的问题，用概率密度的方法提出一个光滑函数，即Sigmoid函数的积分函数，并解决了该光滑函数的误差问题.此后将近10年没有新的研究成果出现，直到2005年，袁玉波等人[6]提出一个多项式光滑函数；2007年，熊金志等人[13]用积分等方法导出一个重要的递推公式，得到一类支持向量机的多项式光滑函数，并指出这类多项式光滑函数有无穷多个；2008年，王斌等人[14]用递推等方法也得到这类多项式光滑函数；2009年，刘叶青等人[10]用级数方法提出这类多项式光滑函数的级数形式.然而，这些方法都没能给出这类多项式光滑函数的误差函数及其性质.到目前为止，有关利用正号函数光滑化的文献也均未给出这种误差函数.因此，支持向量机的多项式光滑函数还存在3个问题：1)用何种方法寻找这类光滑函数的误差函数？2)这类误差函数有多少个？可否用一个一般形式表示？3)这类误差函数的性质如何？为此，本文用Newton-Hermite插值方法，研究支持向量机无穷多个多项式光滑函数的误差函数及其性质，试图解决上述3个长期困扰人们的问题，为光滑函数和支持向量机的研究提供基本的理论支持.

1多项式光滑函数及其Newton-Hermite插值问题

1.1多项式光滑函数

为便于叙述和理解，我们先给出支持向量机多项式光滑函数的定义：

定义1. 多项式光滑函数.在一个包含原点的对称区间[-a,a]，a>0，用一个具有d阶光滑(d为任意正整数)的多项式函数pd(x,a)代替x+=max(0,x)，在该区间以外仍取x+的值.而在端点x=±a上，使pd(x,a)具有d阶光滑，从而使这个函数在整个x轴上皆具有d阶光滑，称这种函数为支持向量机的多项式光滑函数[13],如图1所示的虚线为多项式光滑函数曲线.

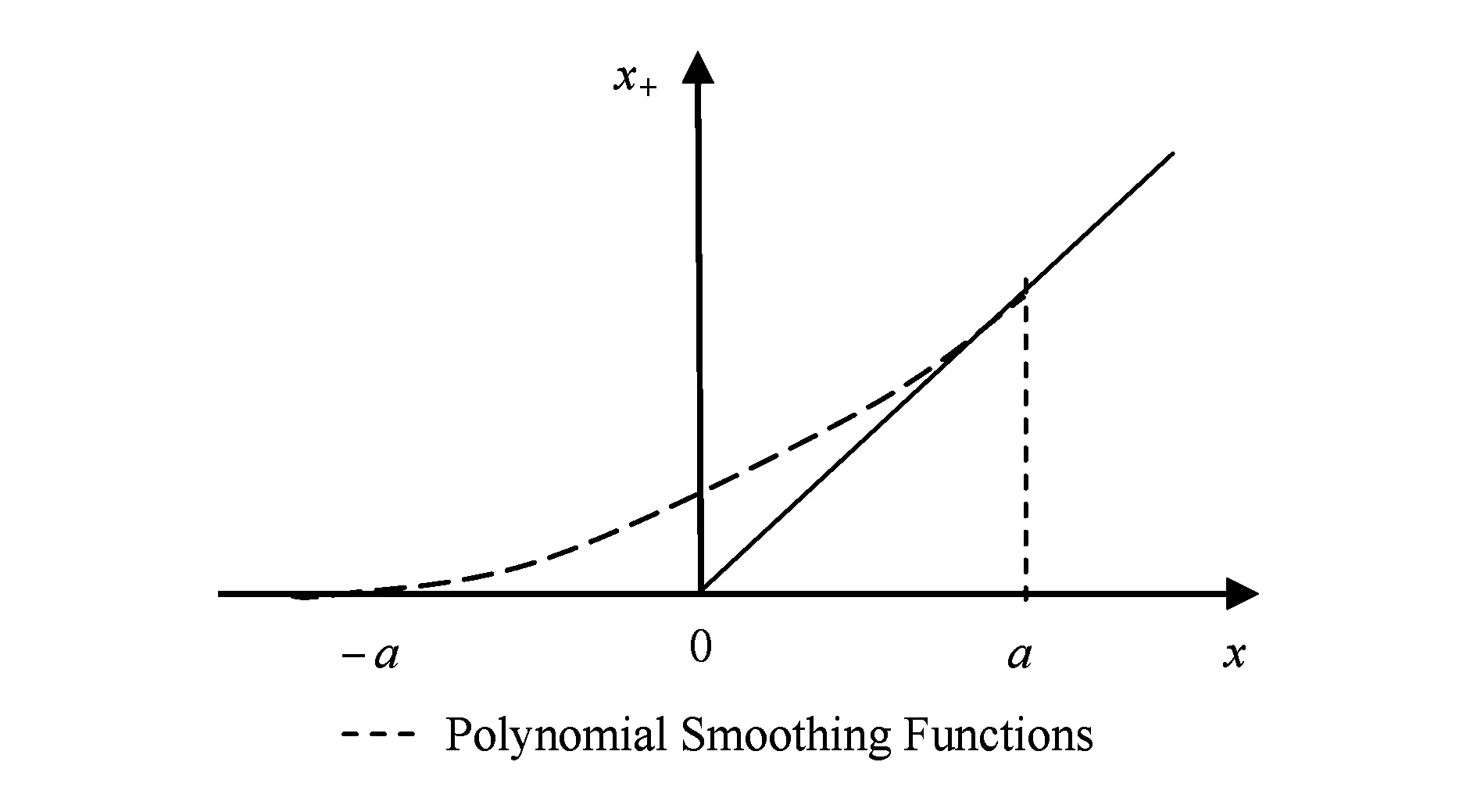
Fig.1　The image of polynomial smoothing functions approximating x+.图1　多项式光滑函数逼近x+的图像

1.2Newton-Hermite插值方法

Hermite插值是处理插值节点处的导数信息已知的一类插值方法.其基本原理是：设被插值函数为f(x)，φ(x)为Hermite插值多项式.给定f(x)在n+1个插值节点x0,x1,…,xn处的函数值及导数值，这些插值条件通常表示为φ(k)(xi)=f(k)(xi),i=0,1,…,n且k=0,1,…,d，其中φ(0)(x)表示函数值φ(x).Newton差商经常被用来求Hermite插值多项式，两者的结合称为Newton-Hermite插值方法.当利用到高阶导数的信息即插值条件中d>1时，Newton-Hermite插值方法具有计算简便、容易得到误差估计等优点[15].

由定义1知，支持向量机的多项式光滑函数只涉及到2个节点，因此下面我们简要给出只有2个插值节点的Newton-Hermite插值的相关定义：

定义2. Newton-Hermite插值多项式函数.给定被插值函数f(x)在2个插值节点x1,x2处的信息f(k)(x1),f(k)(x2)，k=0,1,…,d，若多项式函数φ(x)满足插值条件φ(k)(x1)=f(k)(x1)，φ(k)(x2)=f(k)(x2)，k=0,1,…,d，则称φ(x)为f(x)的Newton-Hermite插值多项式函数.

根据Newton-Hermite插值原理[15]，该多项式函数可表示为

φ(x)=f[x1]+f[x1,x1](x-x1)+…+

f[x1,…,x1](x-x1)d+f[x1,…,x1,x2]×

(x-x1)d+1+f[x1,…,x1,x2,x2]×

(x-x1)d+1(x-x2)+…+f[x1,…,x1,

x2,…,x2](x-x1)d+1(x-x2)d,

其中，插值多项式函数的系数称为Newton差商，其定义如下：

定义3[15]. Newton差商.记

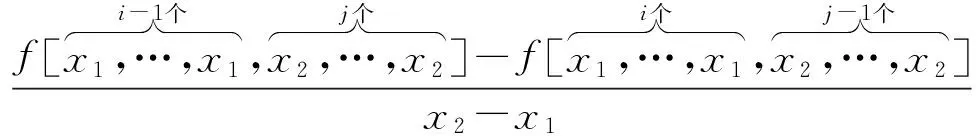
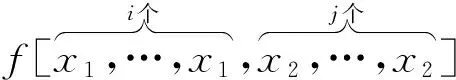
定义4. 误差函数.对插值区间内的任意点x，令R(x)=f(x)-φ(x)，则称R(x)为Newton-Hermite插值多项式函数的误差函数.

根据Newton-Hermite插值原理[15]，该误差函数可表示为

(x-x1)d+1(x-x2)d+1.

(1)

1.3多项式光滑函数的Newton-Hermite插值问题

在支持向量机的光滑理论中，正号函数具有很重要的作用.为表述方便，我们把正号函数记为f(x)，即

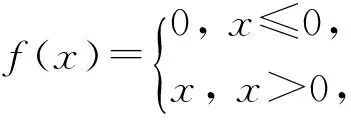
因为正号函数不光滑，所以如何选择光滑函数对正号函数进行光滑逼近是一个重要课题.

本文用多项式函数对正号函数在一个对称区间[-a,a]进行光滑处理，根据定义1，即用d阶光滑多项式函数pd(x,a)来光滑逼近正号函数f(x)，使其满足如下的d阶光滑条件[13]：

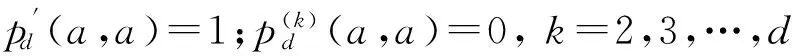
其中a>0，d为任意正整数.根据定义2，显然该问题是一个Hermite插值问题.根据Newton-Hermite插值原理，该d阶多项式光滑函数可表示为

pd(x,a)=f[-a]+f[-a,-a](x+a)+…+

f[-a,…,-a](x+a)d+f[-a,…,-a,a]×

(x+a)d+1+f[-a,…,-a,a,a](x+a)d+1×

(x-a)+…+f[-a,…,-a,a,…,a]×

(x+a)d+1(x-a)d,

(2)

其中,各项系数为Newton差商.

为书写方便，我们结合定义3，记Newton差商为

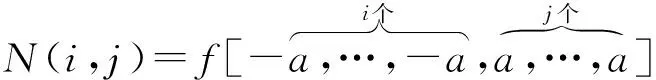
i,j=0,1,…,d+1.

(3)

则由式(2)可直接得d阶多项式光滑函数:

(4)

显然，只要求出各项Newton差商N(i,j)，就可得到多项式光滑函数pd(x,a).因此我们就把求多项式光滑函数的问题转换成了求Newton差商的问题.

2Newton差商与多项式光滑函数的Newton-Hermite插值形式

2.1Hermite插值中的Newton差商

下面的引理表明，在本文的Hermite插值问题中，Newton差商具有许多良好性质.

引理1.Newton差商N(i,j)定义如式(3)，则：

1) N(i,0)=0, i=1,2,…,d+1,

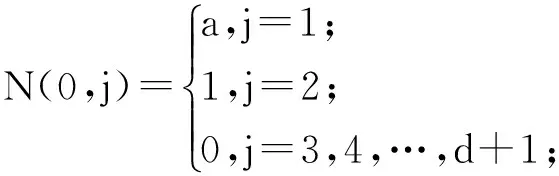
2) 当i≠0，j≠0时，

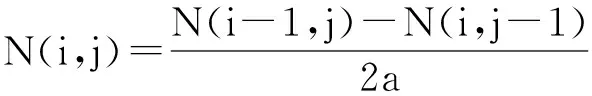
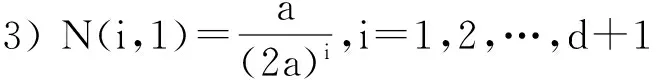
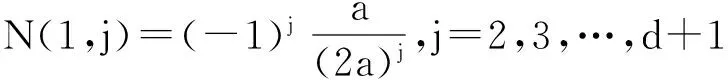
4) 当i≠0，j≠0时，Newton差商为

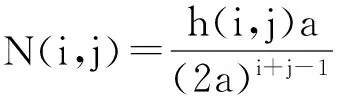
(5)

其中,h(i,j)满足:

h(i,j)=h(i-1,j)-h(i,j-1)；

(6)

5) 当i=1或j=1时，有:

h(i,1)=1，i=1,2,…,d+1,

h(1,j)=(-1)j，j=2,3,…,d+1;

6) 当i,j=2,3,…,d+1时，h(i,j)满足下列递推公式：

证明. 1) 由式(3)得:

N(1,0)=f[-a]=f(-a)=0，

N(0，1)=f[a]=f(a)=a,

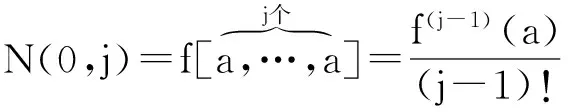
i,j=2,3,…,d+1.

故有N(0,2)=1,N(0,j)=0，j=3,4,…,d+1.

2) 根据式(3)有:

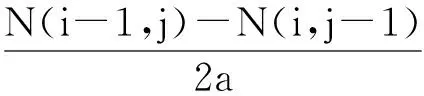
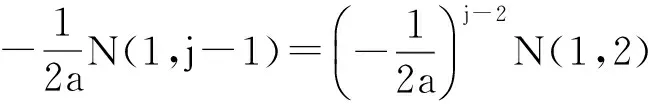
4) 用数学归纳法.

当i+j=2时，有:

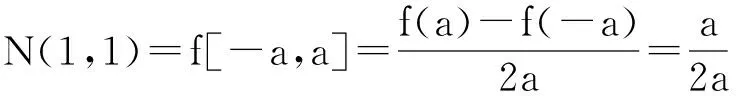
假设当i+j=n时，式(5)成立，即:

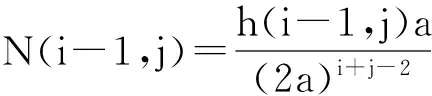
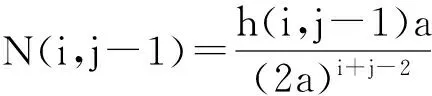
下面证明当i+j=n+1时，式(5)也成立.因为

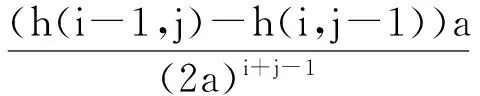
5) 结合3)和式(6)直接可得.

6) 由式(6)分别可得:

h(i,j)-h(i-1,j)=-h(i,j-1)，

h(i-1,j)-h(i-2,j)=-h(i-1,j-1)，

h(2,j)-h(1,j)=-h(2,j-1)，

以上等式相加得到:

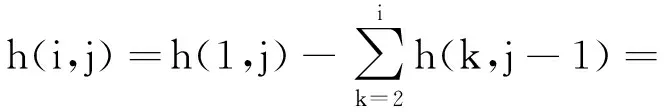
证毕.

说明：

1) 引理1的结论5)，6)表明：系数h(i,j)与插值区间的a无关，只与i和j有关.任意给定i和j，h(i,j)是常量，由引理1的结论5)，6)可将h(i,j)递推出来.为表述方便，我们称h(i,j)为Newton差商因子.

2) 引理1的结论4)把Newton差商表示成式(5)，从而把与a有关的Newton差商N(i,j)与Newton差商因子h(i,j)一一对应了起来，也就是说，把求Newton差商N(i,j)的问题转换成了求Newton差商因子h(i,j)的问题了.

3) 借助Newton差商因子h(i,j)来发现Newton差商的内部规律和性质，仍用Newton差商N(i,j)来更简洁地表示相应的结果.

引理2. 当i，j≠0且i+j>2时，Newton差商因子h(i,j)和Newton差商N(i,j)具有3点性质：

1) 若i+j是偶数，则h(i,j)=-h(j,i)，从而N(i,j)=-N(j,i)；

2) 若i+j是奇数，则h(i,j)=h(j,i)，从而N(i,j)=N(j,i)；

3) N(i,j)=(-1)i+j-1N(j,i).

证明. 用数学归纳法.

1) 当i+j=4时，根据引理1的结论1)～3)，可得：

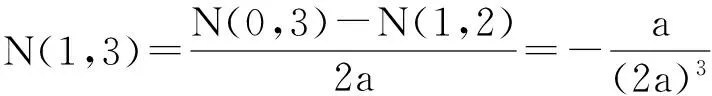
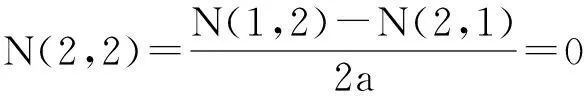
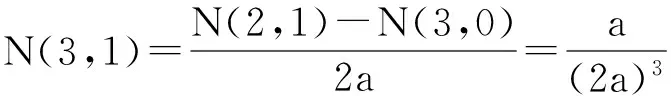
假设当i+j=2n(n>2)时h(i,j)+h(j,i)=0成立.下面证明当i+j=2(n+1)时(n>2)命题也成立.

多次利用式(6)：h(i,j)=h(i-1,j)-h(i,j-1)，可得：

h(i,j)+h(j,i)=h(i-1,j)-h(i,j-1)+

h(j-1,i)-h(j,i-1)=h(i-2,j)-

h(i-1,j-1)-h(i-1,j-1)+h(i,j-2)+

h(j-2,i)-h(j-1,i-1)-h(j-1,i-1)+

h(j,i-2)=[h(i-2,j)+h(j,i-2)]-

2[h(i-1,j-1)+h(j-1,i-1)]+

[h(i,j-2)+h(j-2,i)]，

因为i+j-2=2n,n>2，所以以上每个中括号项都等于0.故h(i,j)+h(j,i)=0成立.

故当i，j≠0且i+j为大于2的偶数时，h(i,j)=-h(j,i)总成立，从而N(i,j)=-N(j,i).

2) 与结论1)类似，可证当i，j≠0且i+j为大于2的奇数时，h(i,j)=h(j,i)总成立，从而N(i,j)=N(j,i).

3) 根据证明1)和2)可直接得到性质3).

证毕.

推论1. 对任意正整数2≤r≤d+1，有h(r,r)=0，N(r,r)=0.

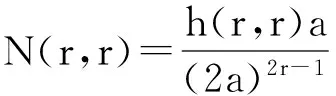
证毕.

推论2. 对任意正整数d，i=1,2,…,d，有(-1)d+1h(i,d+1)>0，(-1)d+1N(i,d+1)>0.

证明. 根据式(5)只需要证明(-1)d+1h(i,d+1)>0成立即可.用数学归纳法.

当d=1时，根据引理1的结论5)知h(1,2)=1，故命题成立.

假设当d=n时命题也成立，即对任意i=1,2,…,n，有(-1)n+1h(i,n+1)>0.

下面证明d=n+1时命题成立.因为：

所以，对任意i=1,2,…,n+1，有：

故对任意正整数d，i=1,2,…,d，(-1)d+1h(i,d+1)>0总成立.

证毕.

推论3. 对任意正整数d，i=1,2,…,d，有(-1)i+1h(d+1,i)>0，(-1)i+1N(d+1,i)>0.

证明. 根据式(5)，只需证明(-1)i+1h(d+1,i)>0成立即可.由引理2，当d+i+1为奇数时，h(d+1,i)=h(i,d+1).所以由推论2，对任意i=1,2,…,d，有：

0<(-1)d+1h(i,d+1)=(-1)d+1h(d+1,i)=

(-1)d+1+2ih(d+1,i)=(-1)i+1h(d+1,i)，

即(-1)i+1h(d+1,i)>0.类似地，当d+i+1为偶数时，h(d+1,i)=-h(i,d+1).所以由推论2，对任意i=1,2,…,d，有：

0<(-1)d+1h(i,d+1)=(-1)dh(d+1,i)=

(-1)d+2i+2h(d+1,i)=(-1)i+1h(d+1,i)，

即(-1)i+1h(d+1,i)>0.

证毕.

2.2多项式光滑函数的Newton-Hermite插值形式

引理3. 支持向量机d阶多项式光滑函数可表示为

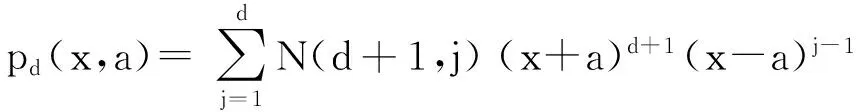
(7)

证明. 由引理1的结论1)知N(i,0)=0，i=1,2,…,d+1，代入式(4)可得：

由推论1知N(d+1,d+1)=0.故有式(7)成立.

证毕.

由引理3知，对称区间(-a,a)上的多项式光滑函数pd(x,a)是2d阶的，于是就推出：

推论4. 文献[6]关于光滑支持向量机在对称区间用“奇数阶多项式可能是做不到的”的猜想是正确的.

结合式(5)和式(7)直接可得：

定理1. 支持向量机d阶多项式光滑函数pd(x,a)可表示为

(8)

定理1表明：

1) 支持向量机的多项式光滑函数存在一种Newton-Hermite插值形式.

2) 只要求出式(8)中的Newton差商因子h(d+1,j)和h(d,j+1)，即可得到这种Newton-Hermite插值形式.

3) 任意给定一个d(d=1,2,…)，式(8)就有一个多项式光滑函数与之对应，显然该Newton-Hermite插值形式含有无穷多个光滑函数，即{pd(x,a),d=1,2,…}.

因此由定理1知，只要求出h(d+1,j)，就可得到支持向量机多项式光滑函数的Newton-Hermite插值形式.于是，我们就把求多项式光滑函数的问题最终转换成了求Newton差商因子h(d+1,j)的问题.

将定理1和引理1结合起来，便可得到如下计算d阶多项式光滑函数的算法：

算法1. 计算支持向量机的任意d阶多项式光滑函数.

Step1. 给定光滑阶数d；

Step2. 根据引理1的结论5)，6)计算Newton差商因子h(d+1,j)，j=1,2,…,d；

Step3. 代入式(8)，计算出d阶多项式光滑函数pd(x,a).

需要指出的是，我们在文献[13]已证明：任意给定一个d(d=1,2,…)，支持向量机的多项式光滑函数是唯一的.因此，由算法1求得的支持向量机多项式光滑函数形式上是用Newton-Hermite插值表示，实际上与文献[10,13-14]的多项式光滑函数是完全相同的，只是求法和形式不同.我们还注意到文献[6,8,10]已做了3个工作：1)列出了这类多项式光滑函数的前3个函数；2)用这类多项式光滑函数提出了多项式光滑的支持向量机及其一般模型；3)做了数值实验.因此本文就不重复这些工作了.

本节得到了Newton差商的性质和多项式光滑函数的Newton-Hermite插值形式，下面我们利用这些结果重点研究多项式光滑函数的误差函数及其性质.

3多项式光滑函数的误差函数及其性质

3.1误差函数及其一般形式

正号函数不是多项式且在原点处不可导，故用插值多项式函数逼近正号函数，必然会产生误差.据我们所知，到目前为止，利用正号函数的光滑化的文献均未解决这类误差问题.下面我们研究多项式光滑函数pd(x,a)逼近正号函数的误差函数.显然误差函数有无穷多个，根据定义4，该类误差函数可记为

Rd(x,a)=f(x)-pd(x,a),

(9)

其中，d=1,2,….

由定义1易知，在区间(-a,a)以外，Rd(x,a)=0,d=1,2,….因此我们只需研究误差函数Rd(x,a)在区间(-a,a)内的情形.

引理4. 对任意点x∈(-a,a)，d阶多项式光滑函数pd(x,a)在x处的误差函数可表示为

(10)

或

(11)

其中,N(d+1,j)和N(j,d+1)由式(5)给出.

证明. 把式(7)代入式(9)直接可得式(10).下面证明式(11)成立.

根据式(1)，正号函数的插值多项式的误差函数也可表示为

(x+a)d+1(x-a)d+1.

若记：

i,j=0,1,…,d+1，

(12)

则误差函数可表示为

Rd(x,a)=l(d+1,d+1)(x+a)d+1(x-a)d+1.

根据定义3，由式(12)可得Newton差商

从而：

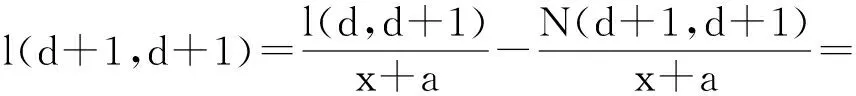
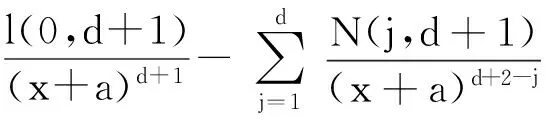
(13)

根据定义3和式(12)可得：

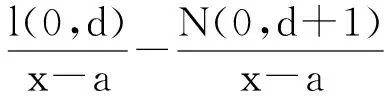
所以：

代入式(13)得到：

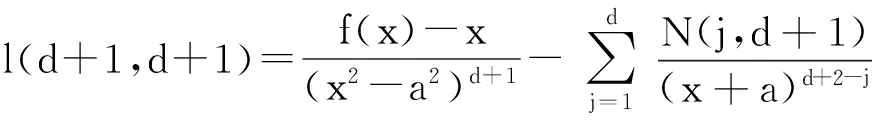
故：

Rd(x,a)=l(d+1,d+1)(x+a)d+1(x-a)d+1=

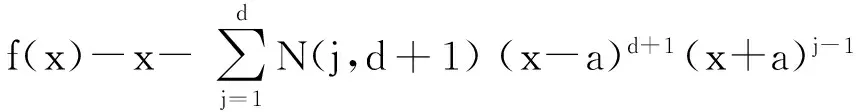
即式(11)成立.

证毕.

定理2. 支持向量机d阶多项式光滑函数的误差函数的一般形式可表示为

Rd(x,a)=

(14)

其中，N(d+1,j)和N(j,d+1)由式(5)给出.

证明. 当x∈(-a,0]时，f(x)=0，代入引理4的式(10)得到：

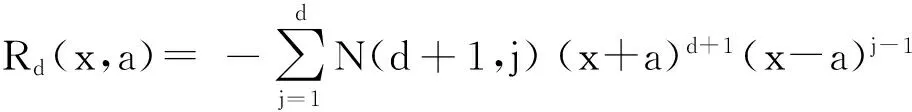
当x∈[0,a)时，f(x)=x，代入式(11)得到：

故(14)式成立.

证毕.

式(14)中含有2类Newton差商N(d+1,j)和N(j,d+1)，通过式(5)可以转化为Newton差商因子h(d+1,j)和h(j,d+1).h(d+1,j)可根据引理1的结论5)，6)得到，而h(j,d+1)可通过引理2间接得到.

定理2表明3个性质：

1) 这类光滑函数的误差函数可由Newton-Hermite插值方法给出.式(14)是这类光滑函数的误差函数的一般形式，也是一个计算误差函数的方便公式，显然只需计算Newton差商因子h(d+1,j)，然后利用引理2计算h(j,d+1)，即可算出N(d+1,j)和N(j,d+1)，j=1,2,…,d，从而由式(14)得到误差函数.

2) 由式(14)知，误差函数与被插值函数的函数值无关，只与Newton差商N有关，或者说只与Newton差商因子h有关(通过式(5)可知).因此我们就把求多项式光滑函数的误差函数问题转换成了求Newton差商的问题，然后又转换成了求Newton差商因子的问题.

3) 任意给定一个d(d=1,2,…)，就有一个误差函数与之对应，显然该误差函数包含了无穷多个多项式光滑函数的误差函数.

以上分析可综合成下面的算法：

算法2. 计算支持向量机d阶多项式光滑函数的误差函数.

Step1. 给定光滑阶数d；

Step2. 根据引理1的结论5)，6)计算Newton差商因子h(d+1,j)；然后根据引理2计算Newton差商因子h(j,d+1)，j=1,2,…,d；

Step3. 将Newton差商因子h(d+1,j)和h(j,d+1)代入式(5),得到N(d+1,j),N(j,d+1)，j=1,2,…,d；

Step4. 将N(d+1,j),N(j,d+1),j=1,2,…,d，代入式(14)计算出d阶多项式光滑函数的误差函数Rd(x,a).

3.2误差函数的性质

定理3. 任意给定正整数d和正数a，支持向量机d阶多项式光滑函数的误差函数Rd(x,a)具有4个性质：

1) Rd(x,a)是非正函数，即Rd(x,a)≤0；

2) Rd(x,a)是偶函数，即Rd(-x,a)=Rd(x,a)；

3) Rd(x,a)在(-a,0]上是减函数，在[0,a)上是增函数；

4) Rd(x,a)在x=0时绝对值最大，即在x=0处误差最大，且最大误差为

证明. 1)当x≤-a或x≥a时，显然有Rd(x,a)=0.下面考虑x∈(-a,a)的情形，此时有x+a>0，x-a<0.

根据推论3可得对任意j=1,2,…,d，有(-1)i+1N(d+1,i)>0.所以当x∈(-a,0]时，

又根据推论2可得：对任意i=1,2,…,d，(-1)d+1N(i,d+1)>0.所以当x∈(0,a)时，

综合以上分析可得：Rd(x,a)≤0.

2) 因为：

Rd(-x,a)=

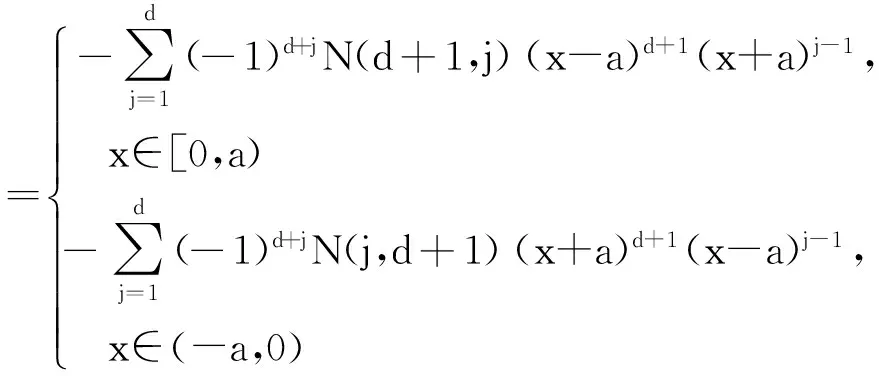
所以Rd(-x,a)=Rd(x,a)，即Rd(x,a)为偶函数、关于y轴对称.

3) 当x∈(-a,0]时，可求得Rd(x,a)关于x的导数：

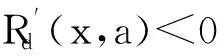
当x∈[0,a)时，可求得Rd(x,a)关于x的导数

4) 根据性质3)的结论，Rd(x,a)在x=0时取最小值.由性质1)知Rd(x,a)≤0，故Rd(x,a)在x=0时绝对值最大，即在x=0处误差最大.在式(14)中取x=0得到最大误差为

证毕.

定理3表明误差函数Rd(x,a)具有若干共同的重要性质，特别是定理3的性质4)给出了误差函数一般形式Rd(x,a)的误差最大值点以及最大误差值，这是误差理论的一个重要内容.

定理4. 任意给定x和正数a，支持向量机d阶多项式光滑函数的误差函数Rd(x,a)关于光滑阶数d是增函数.

证明. 我们在文献[8]中已证明：d阶多项式光滑函数pd(x,a)关于光滑阶数d是减函数，即

pd(x,a)≤pd-1(x,a)，d=2,3,…,

结合式(9)，易得：

f(x)-pd(x,a)≥f(x)-pd-1(x,a)，

d=2,3,…,

即：

Rd(x,a)≥Rd-1(x,a)，d=2,3,…，

所以，Rd(x,a)关于光滑阶数d是增函数.

证毕.

定理3的性质1)表明Rd(x,a)是非正函数，结合定理4知，光滑阶数d越大，Rd(x,a)越接近0.换言之，光滑阶数d越大，多项式光滑函数pd(x,a)越接近正号函数.

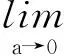
证明. 根据定理3的性质1)，4)有：

故：

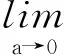
证毕.

3.3误差函数的若干算例

由第3节的证明知：这类多项式光滑函数的误差函数有无穷多个.下面我们以d=1,2,3时为例，即以1阶、2阶和3阶多项式光滑函数为例，用Matlab演算这类多项式光滑函数的前3个误差函数的表达式，以及验证它们的重要性质.

根据算法2，得到表1中关于Newton差商因子h(d+1,j)及h(j,d+1)的数据.

Table1Whendis1, 2and3,theDifferenceQuotientFactorofNewtonh(d+1,j)andh(j,d+1)

表1d值取1,2,3时的Newton差商因子h(d+1,j)及h(j,d+1)

dh(d+1,j)h(j,d+1)11121,-1-1,-131,-2,21,2,2

Note: j=1,2,…,d

当d=1时，1阶多项式光滑函数的误差函数为

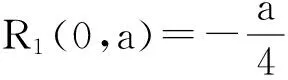
当d=2时，2阶多项式光滑函数的误差函数为

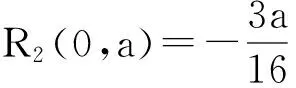
当d=3时，3阶多项式光滑函数的误差函数为

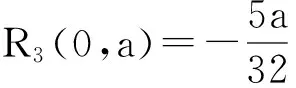
下面以a=1为例，即在区间(-1,1)上，画出1阶至3阶多项式光滑函数的误差函数，如图2所示:

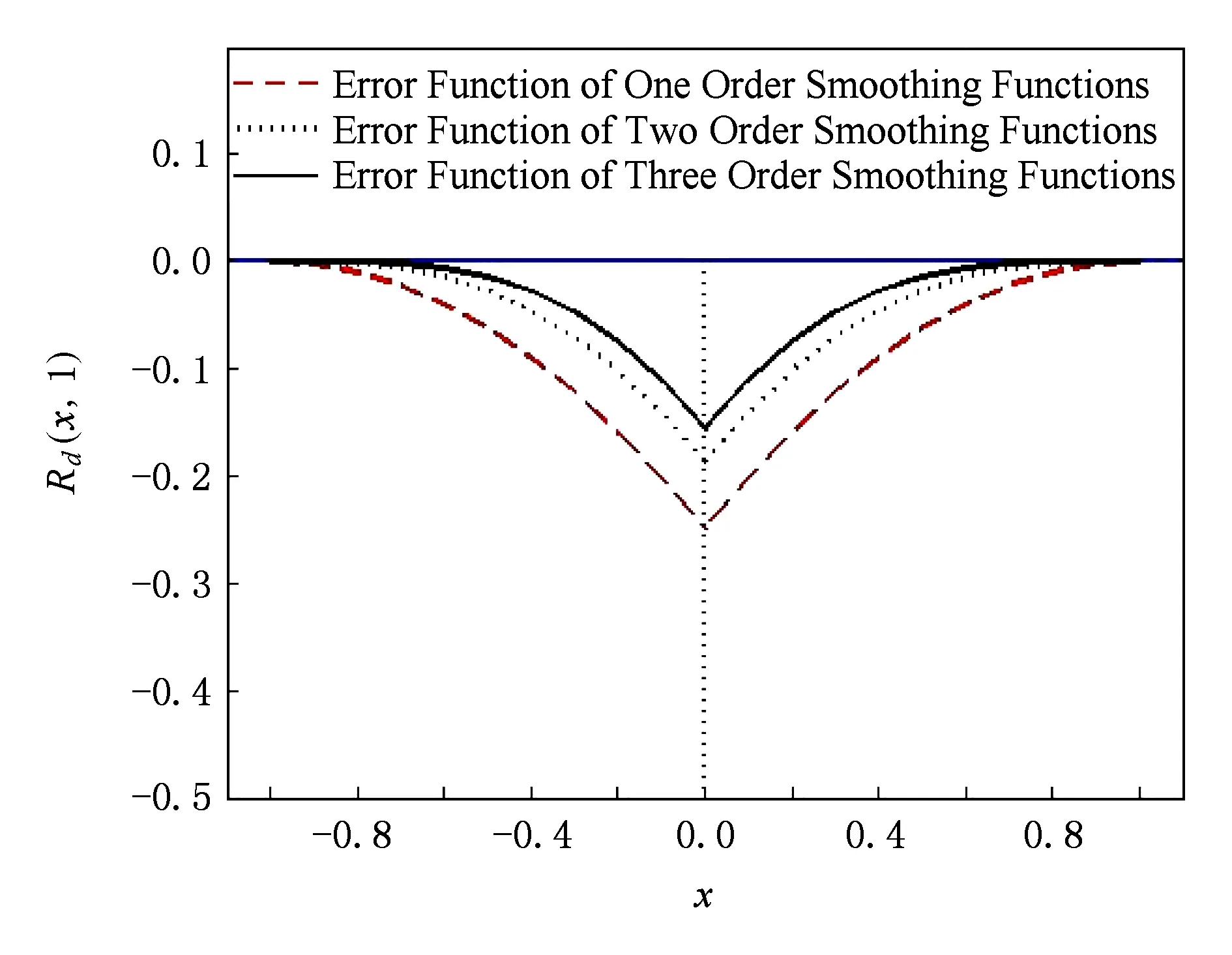
Fig. 2　Error function of the polynomial smoothing functions between -1 and 1.图2　区间(-1,1)上多项式光滑函数的误差函数

由图2可以看出，这3个多项式光滑函数的误差函数具有5个共同的重要性质：1)非正函数；2)偶函数；3)在(-1,0]上是减函数，在[0,1)上是增函数；4)在x=0处误差最大；5)关于光滑阶数是增函数.

4结论

光滑函数是研究光滑支持向量机的重要基础，因此其误差及其性质问题是一个重要的理论问题.近年来多位学者用不同方法对支持向量机的多项式光滑函数进行了研究，提出了这类多项式光滑函数的多种不同形式，还提出了多项式光滑的支持向量机及其一般模型，但都没能解决这类多项式光滑函数的误差函数及其性质问题.为此本文用Newton-Hermite插值方法对该问题进行了研究：首先把多项式光滑函数的误差函数问题转换成Newton-Hermite插值问题，继而转换成求Newton差商的问题，然后转换成求Newton差商因子的问题，最终解决了这个问题,归纳出3个结论：

1) 用Newton-Hermite插值方法可得到这类光滑函数的误差函数.

2) 这类误差函数有无穷多个，任意给定一个光滑阶数，就有一个误差函数与之对应.这无穷多个误差函数可用一个一般形式表示，并给出了这个一般形式,该一般形式能方便地计算出任意多项式光滑函数的误差函数.还给出了误差函数一般形式的误差最大值点以及最大误差值.

3) 这类误差函数具有6个共同的重要性质.如：①都是非正函数；②都是偶函数；③在区间(-a,0]上都是减函数，在区间(0,a)上都是增函数；④误差最大值点都在原点，误差最大值都可由一个公式给出；⑤关于光滑阶数都是增函数；⑥当插值区间趋于一点时，误差都趋于0.

本文用Newton-Hermite插值方法，得到了支持向量机多项式光滑函数的误差函数的一般形式及其许多重要性质，从而解决了这类多项式光滑函数以往没有解决的误差函数问题，成功解决了引言中提到的3个问题，填补了多项式光滑函数在误差函数方面的研究空白，建立了这类多项式光滑函数的误差理论.本文为研究光滑函数和光滑支持向量机提供了基本的理论支持，因而在一定程度上丰富了支持向量机理论.

参考文献

[1]DengNaiyang,TianYingjie.NewMethodinDataMining:SupportVectorMachine[M].Beijing:SciencePress, 2004 (inChinese)(邓乃扬, 田英杰. 数据挖掘的新方法—支持向量机[M]. 北京: 科学出版社, 2004)

[2]XuLL,CrammerK,SchuurmansD.Robustsupportvectormachinetrainingviaconvexoutlierablation[C]Procofthe21stIntConfonArtificialIntelligence.MenloPark,CA:AAAIPress, 2006: 536-542

[3]WuYC,LiuYF.Robusttruncatedhingelosssupportvectormachines[J].JournaloftheAmericanStatisticalAssociation, 2007, 102(479): 974-983

[4]YangXiaowei,TanLiangjun,HeLifang.Arobustleastsquaressupportvectormachineforregressionandclassificationwithnoise[J].Neurocomputing, 2014, 140: 41-52

[5]LeeYJ,MangasarianOL.SSVM:Asmoothsupportvectormachineforclassification[J].ComputationalOptimizationandApplications, 2001, 22(1): 5-21

[6]YuanYubo,YanJie,XuChengxian.Polynomialsupportvectormachine[J].ChineseJournalofComputers, 2005, 28(1): 9-17 (inChinese)(袁玉波, 严杰, 徐成贤. 多项式光滑的支撑向量机[J]. 计算机学报, 2005, 28(1): 9-17)

[7]LeeYJ,HsiehWF,HuangCM. ε-SSVR:Asmoothsupportvectormachineforε-insensitiveregression[J].IEEETransonKnowledgeandDataEngineering, 2005, 17(5): 5-22

[8]XiongJinzhi,YuanHuaqiang,PengHong.Ageneralformulationofpolynomialsmoothsupportvectormachines[J].JournalofComputerResearchandDevelopment, 2008, 45(8): 1346-1373 (inChinese)(熊金志, 袁华强, 彭宏. 多项式光滑的支持向量机一般模型研究[J]. 计算机研究与发展, 2008, 45(8): 1346-1373)

[9]XiongJinzhi,HuJinlian,YuanHuaqiang,etal.Researchonnewsmoothingfunctionsforsupportvectorregressions[J].PatternRecognitionandArtificialIntelligence, 2008, 21(3): 273-279 (inChinese)(熊金志, 胡金莲, 袁华强, 等. 支持向量回归机的光滑函数研究[J]. 模式识别与人工智能, 2008, 21(3): 273-279)

[10]LiuYeqing,LiuSanyang,GuMingtao.Researchonpolynomialfunctionsforsmoothingsupportvectormachines[J].SystemsEngineeringandElectronics, 2009, 31(6): 1450-1453 (inChinese)(刘叶青, 刘三阳, 谷明涛. 光滑支持向量机多项式函数的研究[J]. 系统工程与电子技术, 2009, 31(6): 1450-1453)

[11]ChenC,MangasarianOL.Aclassofsmoothingfunctionsfornonlinearandmixedcomplementarityproblems[J].ComputationalOptimizationandApplication, 1996, 5: 97-138

[12]ChenC,MangasarianOL.Smoothingmethodsforconvexinequalitiesandlinearcomplementarityproblems[J].MathematicalProgramming, 1995, 71: 51-69

[13]XiongJinzhi,HuJinlian,YuanHuaqiang,etal.Anewclassofsmoothingfunctionsforsupportvectormachines[J].ActaElectronicaSinica, 2007, 35(2): 366-370 (inChinese)(熊金志, 胡金莲, 袁华强, 等. 一类光滑支持向量机新函数的研究[J]. 电子学报, 2007, 35(2): 366-370)

[14]WangBin,HuJinlian,XiongJinzhi.Newmethodforsolvingsmoothingfunctionsofsupportvectormachines[J],JournalofSystemSimulation, 2008, 20(15): 4018-4020 (inChinese)(王斌, 胡金莲, 熊金志. 一种求支持向量机光滑函数的新方法[J]. 系统仿真学报, 2008, 20(15): 4018-4020)

[15]KincaidD,CheneyW.NumericalAnalysis:MathematicsofScientificComputing[M]. 3rded.NewYork:ThomsonLearning,Inc, 2002

HeWenbin,bornin1976.PhD,lecturer.Hismainresearchinterestsincluderemotesensingimageprocessing,artificialintelligence.

LiuQunfeng,bornin1978.PhD,associateprofessor.Hismainresearchinterestsincludeglobaloptimization,intelligentcomputing.

XiongJinzhi,bornin1964.Professor.Hismainresearchinterestsincludeartificialintelligenceanddatamining.

收稿日期：2015-01-04；修回日期：2015-08-19

基金项目：国家自然科学基金项目(60773050)；广东省科技发展专项资金(基础与应用基础研究方向)项目(2016A030313135)；东莞市科技计划资助项目(201208102027)

通信作者：熊金志(dgxiongjz@126.com)

中图法分类号TP18

The Error Theory of Polynomial Smoothing Functions for Support Vector Machines

He Wenbin, Liu Qunfeng, and Xiong Jinzhi

(CollegeofComputer,DongguanUniversityofTechnology,Dongguan,Guangdong523808)

AbstractSmoothing functions play an important role in the theory of smooth support vector machines. In 1996, Chen et al proposed a smoothing function of support vector machines—the integral function of Sigmoid function, and solved the error problem of the smoothing function. From 2005 to 2009, Yuan, Xiong and Liu proposed an infinite number of polynomial smoothing function and the corresponding reformulations for support vector machines. However, they did not touch the error functions for this class of polynomial smoothing functions. To fill up this gap, this paper studies the problem of the error functions with the Newton-Hermite interpolation method. The results show that: 1) the error functions of this class of polynomial smoothing functions can be calculated using the Newton-Hermite interpolation method, and the detailed algorithm is given; 2) there are an infinite number of error functions for this class of polynomial smoothing functions and a general formulation is obtained to describe these error functions; 3) there are several important properties for this class of error functions and the strict proof is given for these properties. By solving the problem of the error functions and their properties, this paper establishes an error theory of this class of polynomial smoothing functions, which is a basic theoretical support for smooth support vector machines.

Key wordssupport vector machine; Newton-Hermite interpolation; smoothing function; error function; polynomial

This work was supported by the National Natural Science Foundation of China (60773050), the Special Fund for Science and Technology Development in Guangdong Province (Basic and Applied Basic Research) (2016A030313135), and the Dongguan Science and Technology Plan (2012108102027).