大数据集成中确定数据准确属性值的WR方法

周宁南 盛万兴 刘科研 张 孝 王 珊

1（中国电力科学研究院 北京 100192）2（数据工程与知识工程教育部重点实验室（中国人民大学） 北京 100872）3（中国人民大学信息学院 北京 100872）（zhangxiao＠ruc．edu．cn）

大数据集成中确定数据准确属性值的WR方法

周宁南1，3盛万兴1刘科研1张 孝2，3王 珊2，3

1（中国电力科学研究院 北京 100192）
2（数据工程与知识工程教育部重点实验室（中国人民大学） 北京 100872）3（中国人民大学信息学院 北京 100872）
（zhangxiao＠ruc．edu．cn）

大数据集成是提供高质量数据以进行决策的基础．集成的一个关键环节是根据实体在数据库中的不同元组确定其准确属性值．最新的R－topK方法在数据上实施人工设计的规则确定属性值间的准确程度，得到了相对准确的属性值．然而这种方法在处理多个可能的准确值或设计的规则存在冲突等情况下需要较多人工交互．为此提出基于权重规则的WR（weighted－rule）方法确定大数据集成中数据的准确属性值．该方法为属性值间准确程度的判断规则扩充了权重，在准确值发生冲突时避免了R－topK

方法中人工交互干预．基于追逐过程设计了约束条件推理算法，并证明它能够在O（n2）内推导出每对属性值间的带权重的准确程度，形成推导准确属性值的约束条件．面对约束条件中可能的冲突，提出了目标求解算法，在O（n）时间内从所有属性值组合中搜索最可能的准确属性值．在真实和合成数据集中进行了充分的实验，验证了WR方法的效果和效率．WR方法较R－topK方法在性能上提高了3～15倍，在效果上提升7%～80%．

大数据集成；数据质量；数据准确性；数据清洗；权重规则

随着大数据时代的到来，大数据集成［1］为政府、企业、个人根据数据进行决策提供了数据基础［2－3］．大数据集成由3个环节组成［1－2］．不同数据源中的数据经过第1个环节模式匹配［3］被收集起来，并在第2个环节记录连接［4－5］结束后按照相关的实体分类．面对前2个环节收集到的数据库中同一实体e的记录集合｛t1，t2，…，tk｝，大数据集成的第3个环节提出了数据的准确性问题［2］，即构造目标元组te，使得它对于每个属性A，属性值te［A］都最接近真实值．

一方面，数据的准确性问题在生产中具有迫切需求．据统计，不准确的数据通常占企业数据的1%～5%，对于有些企业，不准确率甚至高达30%［6］．据报道，在美国，不准确的数据每年造成千亿美元的损失［7］．为减少不准确数据带来的危害，数据仓库项目通常需要花费30%～80%的经费和时间用于数据清洗［8］．

另一方面，数据的准确性问题仍然是目前数据库中最具有挑战性的问题之一［4－5，9］．早期的工作主要集中在数据一致性等方面［5－6］．最新的方法R－topK［7］通过定义准确性规则来确定最准确的属性值．但R－topK既不允许规则中存在冲突，也不允许某个实体存在超过一个的目标元组．这导致它在运行过程中需要不断人工调整规则以及为规则不能覆盖的属性设计得分函数来计算top－K准确的属性值．

R－topK方法存在上述缺陷的根本原因在于：多源连接后的数据集中包含庞大的可能准确的属性值组合，而R－topK方法试图利用规则推导出其中最准确的属性值．但是，当推导出的准确属性值存在多个时，很难判断这是因为给定实体本身存在多个准确属性值还是因为规则间存在冲突．因此，遇到这种情况时R－topK方法会重新设计规则或top－K得分函数，其中较多的人工交互阻碍了其在大规模数据上的应用．

在下面的例1中，R－topK方法不能处理2个可能的准确值．

例1．表1以著名运动员Michael Jordan为实体，从包含大数据的互联网上收集了他在1994—1995赛季的得分情况．表2是一些官方机构所维护的十分准确的主数据［8］．主数据表明Michael Jordan在1994—1995赛季分别在篮球联盟NBA和棒球联盟SL打球．

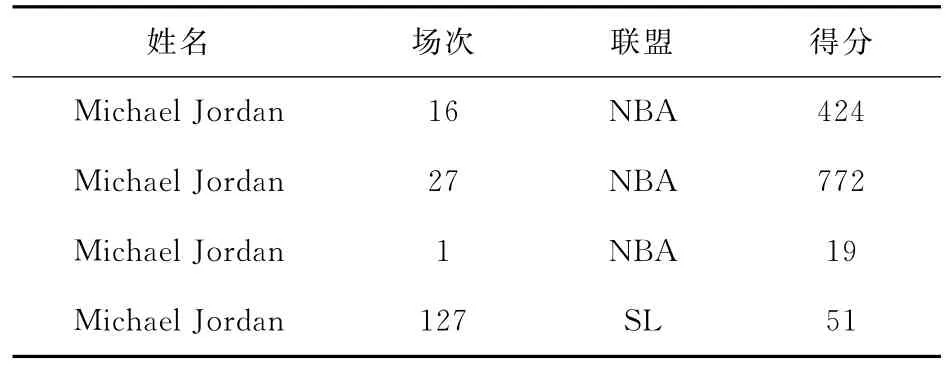
Table 1 Point Table PTfor Michael Jordan in Season 1994—1995表1 Michael Jordan在1994—1995赛季得分情况表PT

Table 2 Master Data Table MDfor Michael Jordan表2 Michael Jordan的主数据表MD

通过对这部分数据进行观察，R－topK认为存在规则“同一联盟的记录中，场次越大，得分越准确”．因此，考虑得分表PT中的第1条元组t1和第3条元组t3，由于t1［场次］＝16＞t3［场次］＝1①，所以元组t1的得分属性值424被认为比元组t3的得分属性值19准确，即t3［得分］≤得分t1［得分］．如果只考虑PT中前3个元组，我们能得到得分属性上3个属性值之间的准确程度（19≤得分424≤得分772）．因此，如果PT表只包含表1中的前3个元组，R－topK可以得到得分属性上最准确的值772．

①在本文中，我们使用t［场次］表示元组t在“场次”属性上的值，用≤得分表示符号左边的属性值的准确程度弱于符号右边的属性值．

但是，由于Michael Jordan在1994—1995赛季同时在2个联盟得分，因此联盟属性上目标元组te存在2个准确值：te［联盟］＝NBA和te［联盟］＝SL．R－topK方法称这种情况不满足“丘奇－罗斯（Church－Rosser）”性质［10］①，不能处理这种情况．遗憾的是，判断数据与规则是否满足此性质需要在运行时判断［7］，这导致R－topK方法在实际数据中需要多次人工设计规则和运行．此外，对于目标元组取值不唯一的情况，R－topK只能舍弃在相关属性上定义规则，改为人工另行设计得分函数求top－K准确的属性值，这严重伤害了方法的准确性，并带来了大量人工交互．

为了克服R－topK方法的这些缺陷，我们给出的权重规则WR（weighted－rule）方法为每个准确性规则设计了权重属性，用来描述规则成立的可能性．利用这些权重，WR方法可以推导出更准确的若干目标元组．例如，我们在表PT和表MD上定义表3所示的规则．其中，R1表示在表MD中出现过的联盟名称也应该出现在目标元组中，这样，我们可以得到te［联盟］＝NBA和te［联盟］＝SL；而R2表示在表PT的联盟属性值相同时，各元组的场次属性值越大，相应元组的得分属性值越准确．这样，我们可以得到19≤得分424和51≤得分51等．注意，由于每条规则带有权重，它们推出的准确程度上的约束条件也带有权重．2．2节详细介绍了约束条件上权重的设置．

Table 3 Weighted Rules表3 扩充权重后的规则

这些规则的权重由人工指定，当人们对规则的正确性不肯定时，权重较小．例如，如果我们对另一条规则R3“目标元组的得分属性值为19”不太肯定时，我们可以把它的权重设置为0．5．我们可以看到，R3和我们从R2得到的19≤得分424和51≤得分51存在矛盾．这时，R－topK方法不能判定19更准确还是424或772更准确．而WR方法利用约束条件上的权值求解目标元组．例如，以〈Michael Jordal，127，SL，51〉和〈Michael Jordal，27，NBA，772〉为目标元组遵循了权重较大的规则R1和R2；而以〈Michael Jordal，1，NBA，19〉为目标元组虽然遵循了权重较小的规则R3，却违反了权重较大的R1和R2．直觉上，遵循权重较大的规则的〈Michael Jordal，127，SL，51〉和〈Michael Jordal，27，NBA，772〉被判定为目标元组．

另一点和R－TopK方法不同的是，指定权重后，WR方法就不再需要人工干预．

本文贡献如下：

1）设计了支持多真值发现和冲突容忍的基于规则的准确性推导方法．特别地，我们提出的为准确性规则扩充权重的WR方法克服了现有方法的缺陷，允许在规则间存在冲突、准确属性值不唯一等情况下寻找目标元组．

2）给出了目标元组求解的高效方法．我们解决了目标元组求解中的重要问题，包括：①证明了以不同顺序实施带权重的规则都能在O（n2）时间内停止并得到同样的结果；②将根据存在冲突的约束条件求解目标元组的问题表达成马尔可夫逻辑网络（Markov logic network，MLN）的推理问题，并利用约束条件的性质提出了O（n）时间的高效求解方法．

3）充分的实验验证和分析．我们使用真实数据和合成数据验证了WR方法的效果和效率．特别地，WR方法在真实数据集上比最新方法快3～15倍，其准确率和召回率比最新方法提高了7%～80%．

1 相关工作

目前数据准确性方面的的大量工作可以分成基于数据一致性的方法和基于真值发现的方法这2类［11］．

1．1 基于数据一致性的方法

基于数据一致性的方法［12－17］假设数据应该满足一组约束．这些约束可以是对数据一致性的要求，比如数据应该满足数据的完整性约束等［13］，也可以是从收集到的数据中挖掘出的条件函数依赖［14］等．通过对收集到的数据进行最少的操作使得这些约束被满足后得到的数据被视为准确数据．

比如，在文献［15］中，条件函数依赖被视为数据应满足的约束，针对具体的函数依赖，元组可以修改函数依赖中被依赖部分的属性值，也可以修改依赖部分的属性值来满足条件函数依赖．由于元组需要

①这里，“丘奇－罗斯”性质指规则按任意顺序施加最终得到的目标元组唯一．进行尽量少的修改使它满足约束条件，但又需要避免与原来的元组过于相似，具体修改方式的选择由对元组中属性值正确性的估计和修改幅度共同决定．类似地，文献［16］采用条件函数依赖作为数据需要满足的约束，并将准确值的寻找映射为超图优化问题，其中启发式的顶点覆盖算法可以确定最少的需要修改的属性值以满足定义的函数覆盖．最近，利用条件函数依赖推导准确程度的关系也被用于寻找不准确的属性值［17］．

考虑到主数据的作用，R－topK方法［7］首次引入了属性的准确值需要满足的规则，并将这些规则施加到数据中得到属性值间准确程度．它对不同属性上的属性值按照准确程度进行拓扑排序，当各个属性上都有某个属性值经过拓扑排序确认准确程度最高时，目标元组由这些准确程度最高的属性值确定．当存在某个属性上有多个最准确的值或规则间存在冲突时，此方法不能求出目标元组．

与这些方法不同，我们扩充了权重的规则不需要收集到的数据完全满足各种依赖关系；同时，本文求解最满足根据规则导出的准确程度约束条件的目标元组允许任意数量的目标元组存在．

1．2 基于真值发现的方法

基于真值发现的方法［18－22］利用对数据源和数据进行建模的方法判断数据的准确值．文献［18］通过数据源的更新历史和数据之间的重复程度利用隐马尔可夫模型判断数据之间的拷贝关系，并使用贝叶斯模型判断准确值．文献［19］通过冗余记录和时效约束在时间戳缺失的情况下辅助恢复数据的时序关系，帮助改善数据质量．文献［20］通过对数据源的可信性和数据内容间的重复性对数据的准确性建模．文献［21］使用概率图模型描述数据源间的可信程度，并为导致错误属性值的原因进行建模．文献［22］使用统计学习方法对数据分布进行建模，并以此求出某些属性上最可能的值．

和基于数据一致性的方法相比，本文的方法为约束或规则附加了它们成立的权重，这允许实际数据违反某些规则，提高了方法的准确性．与基于真值发现的方法相比，我们的方法不需要指定数据源是否可靠和发现其中的时序关系．同时，本文直接求出目标元组，而不是根据一些已知正确的属性值求出另一些未知属性的值．

2 求解目标元组

求解目标元组的过程分为2个部分：1）根据规则得到属性值间准确程度的约束条件及其权重；2）基于约束条件求解最有可能的属性值组合作为目标元组．下面，我们首先在2．1节中介绍扩充权重后的规则，随后的2．2节和2．3节分别介绍目标元组求解的2个过程．

2．1 带权重的规则

扩充了权重的准确规则和R－topK方法中的准确规则类似，均通过元组间属性的值或已判断出准确程度的属性值判断其他属性上属性值的相对准确程度．

准确性规则分为2种：

1）第1规则（α－规则或赋值规则），直接指定目标元组中的属性值，形式定义如下：

［ t（R（t）∧w→te［Ai］＝t［Ai］），p］，

其中，R（t）表示元组t应被包含在某个关系中．w是下列3种谓词组成的合取公式：①t1［Ai］op t2［Ai］，这里op是比较操作符≥，≤等；②ti［Aj］op c，这里c是常数；③t1≤Ait2，这里≤Ai的含义是t1在属性Ai上的值t1［Ai］的准确程度弱于t2在Ai上的值t2［Ai］．p（0＜p≤1）是人们对这条准确规则成立的信心，p越大说明目标元组越应该满足该规则．

例2．以表3中的准确性规则R1为例，元组t被包含在表MD中．元组需满足的条件w为空，即直接指定目标元组的某个属性值．

2）第2规则（β－规则或支配规则），根据某些属性上的值的大小或准确性程度定义其他属性上值的准确性程度，形式定义如下：

［ t1，t2（R（t1）∧R（t2）∧w→t1≤Ait2，p］，

其中，R，w，p的含义和α－规则中的相同．

例3．以表3中的准确性规则R2为例，w是上面提到的形如t1≤Ait2的第3种谓词t1［场次］≤t2［场次］．

为了进行后面的约束条件和准确属性值的推导，我们把上述2种规则中符号→左边涉及到的属性集合记为LAS（R），右边推断出的属性记为RA（R）．

2．2 推导约束条件

为规则扩充权重属性后，属性值应满足的约束条件包括2部分，即准确程度的约束和它对应的权重．下面我们分别介绍：1）如何根据规则推断出准确程度的约束；2）如何求出这些约束条件相应的权重．

2．2．1 推导准确程度的约束

α－规则和β－规则分别可以推断出2类约束条件：1）α－约束条件，形如［te［Ai］＝v，p］，以权重p确定了属性Ai上某个值v与其他值间的准确程度（v比其他值都更准确）；2）β－约束条件，形如［t1≤Ait2，p］，以权重p确定了属性Ai上2个属性值t1［Ai］和t2［Ai］之间的准确程度．我们定义每个约束条件c涉及到的属性为CA（c）．本节求出约束条件中属性的准确程度．

准确程度的获得是一个迭代的过程，其获得的方式分为2种：一种是通过将规则作用于数据，直接得到某个约束条件．例如，通过α－规则［ t（R（t）∧w→te［Ai］＝t［Ai］），p］，直接得出α－约束条件．另一种是通过已经得到的约束条件推断出新的约束条件．比如，根据β－规则［ t1，t2（R（t1）∧R（t2）∧w→t1≤Ait2，p］，如果已经得到准确程度t1≤Ait2和t2≤Ait3，那么就可以推断出新的准确程度t1≤Ait3．这样通过对数据以及已经得到的准确程度施加规则得到新的准确程度的过程称为追踪过程．

与以往追踪方法面临规则冲突就停止不同，本文的算法会继续实施追踪，因此追踪过程能否结束是一个重要问题．定理1表明无论规则的实施顺序，迭代过程可以在O（｜A｜n2）时间内终止，并得到相同的准确程度．其中｜A｜是属性的个数，n是相关实体的记录数．

定理1．追踪过程最多经过O（｜A｜n2）次迭代收敛．

证明．若2次实施规则R得到的结果不同，则存在涉及LAS（R）中属性的新增属性值间准确程度的偏序约束．因为无论新增的偏序对与已有的偏序对是否冲突，在｜A｜个属性上最多有2｜A｜n2个偏序对，因此最多经过2｜A｜n2次迭代即可求出全部约束条件．证毕．

有了定理1的保证，我们设计了CC（construct constraints）算法构造找出属性值间准确程度上的约束条件．

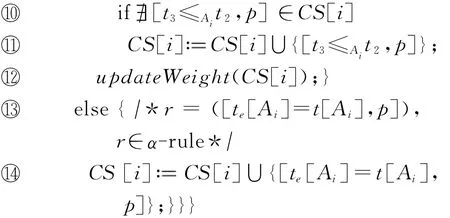
为了快速找到能施加的规则，算法CC首先为规则集合RS中的各个规则按照它们涉及到的属性进行划分（行①）．我们约定2个规则R和R′之间存在依赖当且仅当｜LAS（R）∩RA（R′）｜或｜LAS（R′）∩RA（R）｜不为0．由于规则间有可能存在若干组无关的规则，我们每次迭代一起实施存在依赖的规则（行③～ 瑏瑤）．在对规则追踪过程时，α－规则为目标元组在属性Ai上增加了一个可能取值te［Ai］（行 瑏瑣 瑏瑤）；β－规则在增加了一对属性值上准确程度的同时，还需要计算这时属性Ai上准确程度的传递闭包（行⑥～ 瑏瑣）．由于定理1已经证明了追踪过程最多经过2｜A｜n2次迭代，上述过程直至没有新的准确程度约束出现时终止（行②）．注意，updateWeight使用2．2．2节中介绍的方法计算经过传递闭包产生的约束条件的权重．

例4．以表3中的规则R2为例，假设它的某次实施增加了“424比773的准确程度弱”这样的约束条件；如果之前的迭代已经满足如“19比424的准确程度弱”的约束条件，则根据传递性我们得到“19比773的准确程度弱”这样的准确程度约束．

2．2．2 计算约束条件的权重

2．2．1节中，规则不同的实施顺序得到相同的准确程度；本节中，我们来确定这些准确程度的权重．

属性值和它们之间的准确程度可以用图表示．例1中得分属性上的4对准确程度约束19≤得分424，19≤得分772，424≤得分772和51≤得分51如图1所示．我们把每个属性值的所有存在的取值视为节点，2个节点中有边当且仅当这2个点存在于某个准确程度约束中，边的权重为准确程度约束的权重．可以发现这4个约束可以根据图的连通性分成2组．

Fig．1 An example for constraint condition．图1 一个约束条件的例子

由于图中包含了得分属性上的所有取值，我们可以如下计算每个属性值的正确权重：

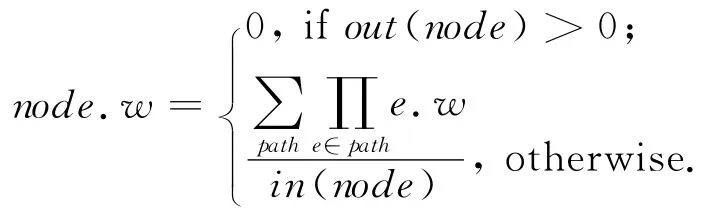
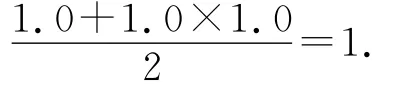
2．3 推导目标元组

在本节中，我们将根据约束条件求解最可能的目标元组．这个问题可以形式化为MLN的推理问题［23］．我们首先形式化目标元组的求解问题，然后针对应用一般MLN求解器求解目标元组的不足，基于约束条件的特点提出求解目标元组的优化算法．

2．3．1 基于约束条件求解目标元组

MLN广泛用于根据一组变量间已有的规则和权重求解这组变量最可能的取值［24］．我们发现可以将本文求解目标元组的问题表达成MLN上的推理问题．利用MLN首先给出某个元组t成为目标元组的可能性，并由此搜索最可能的目标元组．

根据MLN，某个元组t成为目标元组的可能性与该元组满足约束条件的个数和权重有关，其概率

其中，out（node）和in（node）分别代表节点node的出度和入度．当某个节点出度不为0时，它对应的属性值在已有约束中已经比另一属性值准确程度弱，因此它们对应的权重为0．注意，该节点对应的权重为0并不意味着该节点对应的属性值不可能出现在目标元组中，因为第1种约束条件可以直接定义这些属性值存在于目标元组的权重．我们会直接加入这些约束条件（算法1行 瑏瑤），并在求解算法中对它们特殊考虑（算法2行④）．

那些只有入度的节点，在包含它的连通分量做拓扑排序以后存在若干源点到它的简单路径．根据权重计算方法，属性值772对应的权重是每条路径对应的权重的平均值，而每条路径的权重为该路径上准确程度约束的权重的乘积．

例5．以图1中为约束“19≤得分772”计算权重为例，与“得分”属性值772对应的节点具有2条从源点（“得分”属性值1对应的节点）到它的简单路径：19→424→772和19→772．因此，其权重是：化因子，pi是某条约束条件对应的权重，ni（t）＝1时表示元组t满足这个约束条件，ni（t）＝0时表示t不满足．求解目标元组可以看作搜索某一使得P（t＝te｜rules）最大的元组t：

这已经被证明是一个NP－hard问题，但存在高效的求解器，如MaxWalkSAT［25］．这些求解器的基本方法是对某元组各个属性的赋值检查对约束条件的符合与违反程度，并因此修正对元组属性的赋值．限于篇幅，我们这里仅给出应用MLN求解目标元组的一般方法，2．3．2节详细介绍针对约束条件进行优化后的求解算法．

2．3．2 目标元组求解优化

求解过程中贪心和随机策略结合使用避免了陷入局部最优解．但是，在求解目标元组时会导致可能属性值很多、算法运行时间长的问题．本节中我们介绍如何通过对属性的划分加速目标元组的求解．

我们的方法中一共有2类约束条件，它们都针对一个属性，因此优化问题可以重写为

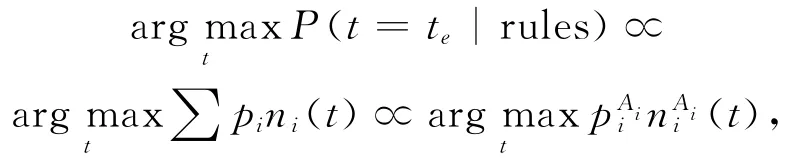
其中，piAi表示CA为Ai的约束条件，niAi（t）表示元组t是否满足这条约束条件①．

如算法TS（target solver）所示，基于重写的优化问题，我们可以得到高效的目标元组求解算法．

①由于满足权重较大的元组也许会违反很多权重较小的元组，因此该问题不是通常的top－K问题．

在CC算法中，每个约束条件c已经根据CA（c）进行了划分（算法1中行⑤⑦）．在算法2中，我们在属性Ai上只考虑图1中没有出度的节点所对应的属性值以及α－约束条件中明确规定的属性值（行③④）．这是因为如果只考虑β－约束，具有出度的节点不会比包含它的连通分量中出度为0的节点代表的属性值更准确．只有当α－约束条件直接要求目标元组取这些节点的属性值时，它们才可能成为准确的属性取值．对于这些可能的取值，我们计算它们对规则的违反程度（行⑤～⑨）．最后，目标元组由各个属性上最可能的取值组成（行 瑏瑡）．由于出度不为0的节点成为候选属性值的情况不超过α－约束的个数，算法2计算各属性上准确值的时间复杂度是O（n）．

例6．根据例5得到的场次属性上的准确程度约束，我们得到A场次．V＝｛127，27｝，类似地，有A场次．V＝｛772，51｝等．最终，利用各个属性上的准确属性值的笛卡儿积和现有元组进行交集，我们得到例1中的2个目标元组：〈Michael Jordal，127，SL，51〉和〈Michael Jordal，27，NBA，772〉．

3 实验结果与分析

本节中我们同时使用真实和合成数据验证本文方法的性能与效果．我们使用最新方法R－topK作为基线方法．特别地，实验说明了下述问题：1）本文为规则扩充权重后的方法比只使用规则的推理方法更高效；2）本文设计的存在冲突的规则提升了寻找准确值的效果；3）本文中各规则权重的设置是健壮的．

3．1 实验环境与数据集描述

我们使用C＋＋实现本文方法WR，实验环境是一台Linux服务器，英特尔至强E5645 2．4GHz处理器，8GB内存，1TB SATA硬盘．除了R－topK方法用于进行性能和效果的比较外，我们还实现了其他具有代表性的若干方法：DeduceOrder［18］，copyCEF［16］以及对属性值进行计数的voting方法．

我们使用3个被广泛使用的公开数据集（Med，CFP和Rest）以及合成数据集（Syn）．公开数据集分别包含了不同公司的医药销售数据、论文征稿数据和餐厅营业数据．合成数据集由向例1中的PT和MD表添加随机选中的数据产生．它们的数据大小和使用规则的情况如表4所示：

Table 4 Dataset and Rules表4 数据集及使用的规则

3．2 运行时间

我们使用Med，CFP，Syn共3个数据集测试本文的方法和最新方法针对不同大小的元组个数和不同数量的规则情况下的运行时间．

图2使用Med和CFP数据集在规则数量大致相同时测试2种方法在不同元组个数情况下的运行时间．这2种方法的运行时间包括2部分，即寻找约束条件及目标元组求解．

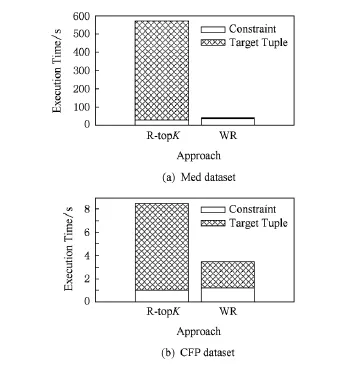
Fig．2 Performance comparison of WR and R－topKin real dataset．图2 真实数据集上WR与R－topK方法的性能对比

从图2（a）可以看出，2种方法计算约束条件的时间相当，其中WR方法由于还要计算约束条件的权重，用时比R－topK方法多10%左右．但由于R－topK还需要运行top－K算法，用时远远超过WR算法求解目标元组的时间．这是因为R－topK方法需要为很多属性值求可能性，但通过对遵循和违反约束条件情况的分析，本文的目标元组求解算法过滤掉了大部分需要在最新的方法中考虑的属性值．

图2（b）使用CFP数据集的结果也可以看出，在数据规模大幅增加的情况下，WR具有比R－topK用时少的趋势．当数据集中元组数增多从而每个属性上可能的属性值增多时，WR算法用了更少的时间．

图3使用Syn数据集测试元组数量、规则数量以及主数据规模对WR性能的影响，它们的初始值分别被设为3×107，3×106，3×103．图3（a）～（c）是依次修改这3个变量的实验结果．为简洁起见，图3中分别用Ntuples和Nrules表示元组数和规则数．

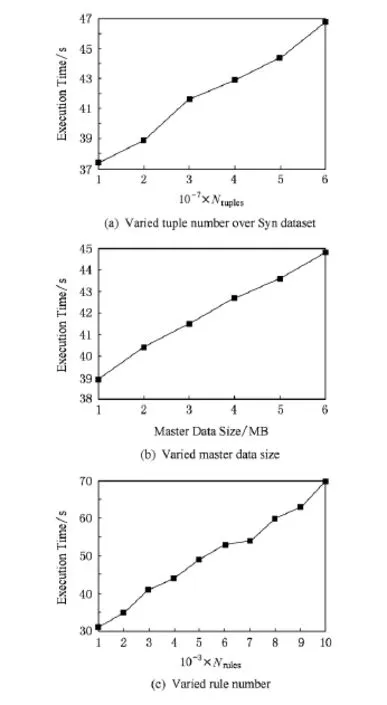
Fig．3 Performance of WR approach in Syn dataset．图3 Syn数据集上WR方法性能实验

图3（a）中，数据规模每增加1 000万个元组，运行时间增加小于2s，这部分增加的时间主要来自于约束条件的寻找；而图3（b）显示主数据规模对运行时间影响不大；图3（c）中，每增加1 000个规则，运行时间增长2s左右．图3中的数据说明WR方法对数据规模、规则个数是可扩展的．

3．3 准确性

我们使用3个真实数据Med，CFP，Rest比较WR方法和4种最新的已有方法（DeduceOrder，copyCEF，voting，R－topK）的准确性．我们只考虑只具有一个目标元组的实体以有利于这些方法．

并非所有方法都在3个真实数据集上进行了实验：1）DeduceOrder方法需要数据集中存在CFD，但Med数据集中不存在这种函数依赖；2）copyCEF方法需要在数据集中寻找重复的数据，它所需要的数据只有Rest数据集中存在；3）剩下的voting，R－topK，WR方法在3个数据集上都进行了实验．

1）Med数据集上的结果．

voting，R－topK和我们的方法找到的目标元组中正确的分别占45%，80%，90%．其中R－topK方法也考虑过在WR方法中被判定为目标元组的若干元组，但由于这些元组和其他目标元组存在规则上的冲突，R－topK方法为了让规则满足大多数目标元组，将它们舍弃．

2）CFP数据集上的结果．

CFP数据集的结果和Med数据集的结果类似，voting，DeduceOrder，R－topK，WR找到的目标元组中正确的分别占37%，0%，70%，89%．由于CFP数据从多个数据源爬取得到，为它设计规则很难避免冲突，这时WR方法比R－topK方法的效果更好．

3）Rest数据集上的结果．

Rest数据集只需要判断一个属性值是否准确，因此我们使用准确率、召回率和F1－measure［26］来比较我们的方法和现有方法的效果．

如表5所示，DeduceOrder实现了100%的准确率，但只有15%的召回率，因此F1－measure只有0．26．而voting方法的召回率可以达到74%，但其准确率只有60%．copyCEF在具有不同时期冗余数据的Rest数据集上可以实现准确率和召回率的平衡（分别是76%和85%），因此收获了较高的F1－measure值0．83．但基于规则的R－top K方法和WR方法更好．由于WR允许对若干规则的违反，其准确率92%和召回率95%都高于目前最新方法R－topK的81%和90%．

Table 5 Accuracy Comparison on Rest Dataset表5 Rest数据集上的准确性比较

3．4 冲突与权重敏感程度

我们在3个真实数据集上测试了规则的冲突情况和我们的方法对规则权重的敏感程度．图4显示了我们的方法在3个数据集上分别有10%，13%，17%的规则是存在冲突的．这些冲突的规则在R－topK算法中只能被去掉，当我们把这些规则去掉后，WR的准确率和召回率有了5%～10%的下降．

Fig．4 Ratio of rule confliction．图4 冲突规则比率

为了检查WR方法是否对规则的权重敏感．我们对各个规则的权重进行小范围的随机调整，然后检测WR方法的准确性．3个数据集的准确性随权重变化的情况类似，限于篇幅，我们只在图5中展示Rest数据集上的情况．可以看出，当规则的权重在10%的范围内改变时，Rest数据集上准确率和召回率的影响不超过5%．其中，准确率随着离最优的权重幅度越远，准确率均匀下降．但召回率在权重小幅度上升时下降较慢，而在权重小幅度下降时下降较快，这是因为大部分规则不存在冲突，但小部分存在冲突的规则会产生以下正确的目标元组．当全部规则的权重都小幅度下降时，这部分元组会被其他元组取代，导致召回率快速下降．

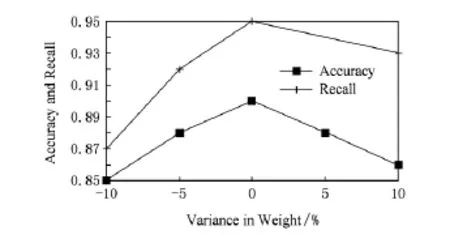
Fig．5 Sensitivity of weight in rules in Rest dataset．图5 Rest数据集对权重敏感程度

4 结束语

为寻找实体相对准确的属性值这一大数据集成中的关键步骤，本文提出了为规则扩充权重的WR方法，它克服了现有方法在多准确值发现和不支持冲突规则的缺陷．特别地，为实施带权重规则推导约束条件的追踪过程，我们提出了在O（n2）时间停止的算法，为基于约束条件搜索准确属性值的问题，提出基于马尔可夫逻辑网络（MLN）的线性高效求解算法．真实数据集与合成数据集上的充分实验证明WR方法在性能上有3～15倍的提升，在目标元组的准确率和召回率上提高了7%～80%．

［1］Dong Xin Luna，Srivastava D．Big data integration［C］??Proc of ICDE 13．Piscataway，NJ：IEEE，2013：1245 1248

［2］Dong Xin Luna，Srivastava D．Big data integration［J］．Proceedings of the VLDB Endowment，2013，6（11）：1188 1189

［3］Bellahsene Z，Bonifati A，Rahm E．Schema Matching and Mapping［M］．Berlin：Springer，2011

［4］Gelman I．Setting priorities for data accuracy improvements in satisficing decision－making scenarios：A guiding theory［J］．Decision Support System，2010，48（1）：507 520

［5］Getoor L，Machanavajjhala A．Entity resolution：Theory，practice ＆open challenges［J］．Proceedings of the VLDB Endowment，2012，5（12）：2018 2019

［6］Fan Wenfei．Querying Big Social Data［M］．Berlin：Springer，2013：14 28

［7］Cao Yang，Fan Wenfei，Yu Wenyuan．Determining the relative accuracy of attributes［C］??Proc of SIGMOD 13．New York：ACM，2013：565 576

［8］Radcliffe J，White A．Key issues for master data management，G00210255［R］．Stanford，CT：Gartner，2008

［9］Fan Wenfei，Geerts F，Nan Tang，et al．Inferring data currency and consistency for conflict resolution［C］??Proc of ICDE 13．Piscataway，NJ：IEEE，2013：470 481

［10］Abiteboul S，Hull R，Vianu V．Foundations of Databases［M］．Reading，MA：Addison－Wesley，1995

［11］Yakout M，Elmagarmid A，Berti－Equille L．Don t be SCAREd：Use scalable automatic repairing with maximal likelihood and bounded changes［C］??Proc of ACM SIGMOD 13．New York：ACM，2013：553 564

［12］Firestone J．Enterprise information portals and knowledge management［M］．New York：Routledge，2003

［13］Bertossi L，Arenas M，Chomicki J．Consistent query answers in inconsistent databases［C］??Proc of PODS 99．New York：ACM，1999：68 79

［14］Fan Wenfei，Geerts F，Kementsietsidis A．Conditional functional dependencies for capturing data inconsistencies［J］．IEEE Trans on Database System，2008，33（1）：1 48

［15］Kolahi S，Lakshmanan L．On approximating optimum repairs for functional dependency violation［C］??Proc of ICDT 09．New York：ACM，2009：53 62

［16］Ma Shuai，Fan Wenfei，Cong Gao．Improving data quality：Consistency and accuracy［C］??Proc of PVLDB 07．Berlin：Springer，2007：315 326

［17］Blanco L，Crescenzi V，Merialdo P，et al．Probabilistic models to reconcile complex data from inaccurate data sources［C］??Proc of AISE 10．Berlin：Springer，2010：83 97

［18］Dong Xin Luna，Berti－Equille L，Srivastava D．Truth discovery and copying detection in a dynamic world［C］?? Proc of VLDB 09，Berlin：Springer，2009：562 573

［19］Li Mohan，Li Jianzhong，Gao Hong．Evaluation of data currency［J］．Chinese Journal of Computers，2012，35（11）：2348 2360（in Chinese）（李默涵，李建中，高宏．数据时效性判定问题的求解算法［J］．计算机学报，2012，35（11）：2348 2360）

［20］Galland A，Abiteboul S，Marian A，et al．Corroborating information from disagreeing views［C］??Proc of WSDM．New York：ACM，2010：131 140

［21］Koudas N，Sarawagi S，Srivastava D．Record linkage：Similarity measures and algorithms［C］??Proc of ACM SIGMOD 06．New York：ACM，2006：802 803

［22］Fan Wenfei，Geerts F．Foundations of Data Quality Management［M］．San Rafael，CA：Morgan Claypool Publishers，2012：1 20

［23］Richardson M，Domingos P．Markov logic networks［J］．Machine Learning，2006，62（1）：107 136

［24］Domingos P，Lowd D．Markov Logic：An Interface Layer for Artificial Intelligence［M］．San Rafael，CA：Morgan Claypool Publishers，2009

［25］Manya F，Argelich J．Exact Max－SAT solvers for overconstrained problems［J］．Journal of Heuristics，2006，12（4）：375 392

［26］Baeza－Yates R，Ribeiro－Neto B．Modern Information Retrieval［M］．New York：ACM，1999

Zhou Ningnan，born in 1990．Currently PhD candidate at Renmin University of China．His research interest includes high performance database． Sheng Wanxing，born in 1965．Received his BSc，MSc and PhD degrees from Xi＇an Jiaotong University．Full professor in China Electric Power Research Institute（CEPRI），Beijing，China，since 1997．His research interests include renewable energy generation and grid－connected technologies． Liu Ke－yan，born in 1979．Received his PhD degree in electrical engineering from Beihang University in 2007．Currently，senior researcher in China Electric Power Research Institute．His current research interests include distributed generation（DG），planning and operation analysis of distribution systems，power system computation method and simulation．

Zhang Xiao，born in 1972．PhD．Associated professor at Renmin University of China．His research interests include database architecture and big data management．

Wang Shan，born in 1944．Master．Professor and PhD supervisor at Renmin University of China．Her research interests include high performance database，main memory database and data warehouse．

WR Approach：Determining Accurate Attribute Values in Big Data Integration

Zhou Ningnan1，3，Sheng Wanxing1，Liu Ke－yan1，Zhang Xiao2，3，and Wang Shan2，31（China Electric Power Research Institute，Beijing100192）2（Key Laboratory of Data Engineering and Knowledge Engineering（Renmin University of China），Ministry of Education，Beijing100872）3（School of Information，Renmin University of China，Beijing100872）

Big data integration lays the foundation for high quality data－driven decision．One critical section thereof is to determine the accurate attribute values from records in data pertaining to a given entity．The state－of－the－art approach R－topKargues to design rules to decide relative accuracy among the attribute values and thus obtain accurate values．Unfortunately，in cases where multiple true values or conflicted rules exist，it requires rounds of human intervention．In this paper，we propose a weighted rule（WR）approach for determining accurate attribute values in big data integration．Each rule is augmented with weight and thus avoid human intervention when conflicts occur．This paper designs a chase procedure－based inference algorithm，and proves that it can figure out weighted constraints over relative accuracy among attribute values in O（n2），which introduces constraints for finding accurate data values．Taking conflicts among constraints into consideration，this paper proposes an O（n）algorithm to discover accurate attribute values among the combination of data values．We conduct extensive experiments under real world and synthetic datasets，and the results demonstrate the effectiveness and efficiency of WR approach．WR approach boosts performance by

TP311

2014－11－24；

2015－03－24

国家“九七三”重点基础研究发展计划基金项目（2014CB340403）；国家电网公司研究项目（EPRIPDKJ［2014］3763号）

This work was supported by the National Basic Research Program of China（973Program）（2014CB340403）and the Project of State Grid Corporation of China Research Program（EPRIPDKJ［2014］No．3763）．

张孝（zhangxiao＠ruc．edu．cn）

factor of 3 15xand improves effectiveness by 7%80%．Key words big data integration；data quality；data accuracy；data cleaning；weighted rules