用于固体矿床多分量感应测井响应模拟的矢量有限元法

王健, 陈浩, 王秀明

1 中国科学院声学研究所声场与声信息国家重点实验室， 北京　100190 2 中国科学院大学， 北京　100049



用于固体矿床多分量感应测井响应模拟的矢量有限元法

王健1,2, 陈浩1, 王秀明1

1 中国科学院声学研究所声场与声信息国家重点实验室， 北京100190 2 中国科学院大学， 北京100049

摘要本文开发了基于非结构化四面体网格的三维矢量有限元法，实现了固体矿床井眼中多分量感应测井响应的数值模拟，并分析了多分量感应测井仪器在复杂矿床模型中的响应特征.本文通过采用几何因子背景场，有效地避免了源的奇异性问题；同时，在井眼边界采用非均质网格并用Gauss-Legendre积分计算四面体单元的等效电导率.利用LU分解求解线性方程组，实现了一次网格划分多点的数值计算，提高了计算效率，从而实现快速连续的多分量感应测井模拟.非结构化的四面体网格确保了该方法可以模拟实际问题中所能遇到的复杂的矿体模型.基于水平三层分层和径向分层模型，验证了算法在各向同性和各向异性介质中的可靠性.我们还以三个不同的矿床模型为例，研究了多分量感应测井仪的不同分量的探测特性，结果表明，结合九个分量的信息，可以探测矿体的深度，也可以识别矿体的方位和走向，为精确地描述矿体的三维分布特征打下了基础.

关键词矢量有限元； 多分量感应测井； 固体矿床

Due to the characteristic of solid deposit, such as wide variety, complex distribution, we use the vector finite element method to simulate the response of multicomponent induction instrument, which has an advantage for medium with complex structure and boundary based on unstructured mesh. Moreover, the method could avoid defects of nodal finite element method. Specifically, geometry factor background field is used to eliminate the singularities of source efficiently. Meanwhile, heterogeneous grids are introduced at the boundary of the borehole and the equivalent conductivities of the tetrahedron elements are calculated by using Gauss-Legendre integral. To take advantage of the LU decomposition to solve the linear system of equations, we could obtain multipoint numerical results for each meshing. It greatly improves the efficiency. So as to ensure a rapid and successive simulation of the multicomponent induction logging.

It has been tested and verified that this method is valid and reliable in the isotropic and anisotropic medium based on the horizontal three-layered and radial model. In the dipping layered formation, all nine components are studied. TheXXandYYresponses are more sensitive to the dipping angle than theZZwith sharp dipping angle; the cross-componentsXZandZXare influenced by border and anisotropy. The apparent conductivity curves ofXZandZX-components show horns in the opposite direction. While in the spherical and cylindrical ore body model, we show azimuthal sensitivity of all nine components of apparent conductivity. Circle lines for response ofZZ-component confirm that the lack of azimuthal sensitivity of the conventionalZZ.The remaining eight components do show azimuthal sensitivity, but four of them (XX,XY,YY,YX) have the period of 180°, while the other four (XZ,YZ,ZX,ZY) have the period of 360°.It is quite obvious that having any combination of measurement from the first group will not allow a resolution between left and right because of the 180°symmetry. The pairs of signals from the second group (ZX,ZY) or (XZ,YZ) uniquely define the azimuthal direction of the ore body.

We develop a three dimensional vector finite element program for multicomponent induction logging based on unstructured tetrahedral mesh in frequency domain, then we use it to simulate the response of multicomponent instrument in solid deposit. The numerical results show that it is able to identify anisotropy of ore body as same as in oil and gas reservoir. TheZZ-component indicates the vertical conductivity, and theXXandYY-components indicate the horizontal conductivity. The cross-componentsXZ,ZX,YZ,ZYhave the period of 360°, therefore provide azimuthal information by which you could laid a foundation to accurately describe the distribution of ore deposit.

1引言

自从Doll(Doll,1949)提出了几何因子理论以来，感应测井在油气储层勘探和开发中得到了广泛的应用(Moran and Kunz,1962).这种方法通过测量井下的载流线圈在井附近介质中产生的感应电流所形成的二次场与周围介质电导率的密切关系来获得介质的电导率信息.在矿床勘探中，应用感应测井方法识别电性异常和磁性异常矿床的想法早已有之(Broding et al.,1952;Cheryauka and Sato,2002).然而，包括感应测井方法在内的测井方法在矿床勘探中的应用迄今远不如在石油勘探中普及.矿床测井发展比较滞后的主要原因是长期以来矿床的勘探和开采主要集中在浅部，钻井和取样成本比较低，因而对矿床的精细评价主要是对取样的矿体进行直接的测量，而非石油勘探中的间接的地球物理测量(Baltosse and Lawrence,1970).但是随着矿床的埋深增加，地面地球物理方法的分辨率和精度降低，钻井和取样成本增加，人们开始逐步重视测井方法在深部矿床勘探中的作用.目前一些井中地球物理方法已经在深部找矿中取得了良好的效果.例如：加拿大的萨德伯里铜、镍矿区通过深部钻孔中瞬变电磁方法组合，从20世纪80年代中期以来相继发现了一批深部铜、镍硫化物矿床(滕吉文等，2007).虽然矿床测井与石油测井有一定的相似性，但前者也有独特之处：除了矿床种类繁多以外，固体的矿床分布复杂，形态多样，空间分布有限，由此矿体的岩石物理模型一般都为复杂的三维模型，而油气多为层状的二维模型，因此对矿体的空间分布的评价除了要给出矿体的深度信息，还要求给出矿体的方位和走向信息.

多分量感应测井仪器由正交的三个发射线圈和正交的三个接收线圈系阵列组成，能够测量XX，YY，XY，YX，XZ，YZ，ZX，ZY和ZZ分量(Kriegshauser et al.,2000;Zhdanov et al.,2001).其中分量的第一个字母代表发射线圈的方向，第二个字母代表接收线圈的方向.对这些分量的分析处理能够识别储层或矿体的各向异性电导率、裂缝、断裂、矿体边界、方位和走向等信息.因此该方法在未来的矿床评价中会有独特的优势，但要从九个分量中正确获取这些信息远比只从ZZ分量进行电导率评价时困难的多(Rabinovich et al.,2006;Davydycheva,2010;肖加奇等,2013)，因此需要开展大量的理论研究和数值模拟分析，充分了解和认识不同分量的探测特性，并进一步提出反演或评价的方法.目前有关多分量感应测井的研究大多是针对具有平面分布特征的油气储层(Wang et al.,2008;汪宏年等,2008；魏宝君等,2009;Davydycheva et al.,2009)，而对其在具有复杂结构分布的固体矿床勘探中的研究则较少.

在电磁场正演模拟中，最常用的数值方法是有限差分法(Finite difference method:FDM)和有限元法(Finite element method:FEM)，其他数值方法诸如积分方程法(Avdeevet al.,2002;Fang et al.,2006)和有限体积方法(Weiss,2013)也有一定的应用.有限差分法广泛用于解决2-D和3-D时域和频域问题(Newman and Alumbaugh,1995;Weiss and Newman,2002).基于结构化网格的有限差分方法比有限元方法更容易实现，但它对网格进行局部优化十分困难，任何网格尺寸的改变对于整个问题的计算量有很大的影响(Puzyrev et al.,2013).而且由于复杂的模型边界不能够用矩形网格精确的近似从而对结果的精度造成极大的影响.因此如果目标模型是复杂的几何体，有限元法由于支持非结构化的网格而显得更有优势.其所产生的网格能够准确地模拟复杂边界和高电导率对比度的情况，这种情况仅需在介质的分界面、源和接收器处进行精细的网格划分.

在电磁勘探中，有限元方法虽然已经得到了广泛应用(Chang and Anderson,1984;Key and Ovall,2011;da Silva et al.,2012)，但也还存在二个不足.(1)传统的节点有限元方法不能够正确处理介质分界面处电场强度法向方向的不连续性.(2)有散度不等于0的非物理解存在(Jin,2002).对于上述问题，一种解决的办法是用规范的磁矢势方程(Biro and Preis,1989;Badea et al.,2001)而不是直接的电场强度E或者磁场强度H方程.另一种方法是选用矢量有限元方法(Nédélec,1980;孙向阳等,2008;Li et al.,2011;Mukherjee and Everett,2011)，它的自由度是沿单元边的切向分量.矢量有限元在单元内强加了散度为0的条件，并允许界面处的电场强度法向分量的不连续性.

本文采用基于非结构化四面体网格的三维矢量有限元方法对多分量感应测井仪器的响应进行数值模拟.首先，给出了矢量有限元在各向异性电导率介质中的原理与方法.其次，通过与解析结果的对比验证了方法和代码的正确性并分析了井眼网格剖分方法对数值精度的影响.然后，模拟了多分量感应测井仪器在倾斜各向异性地层中的响应，分析了倾角和各向异性对九个分量的影响，着重分析了交叉的XZ和ZX分量的曲线特征.最后对距井壁一定距离的球形矿体和倾斜的圆柱状矿体计算了仪器相对于矿体旋转时不同分量所具有的探测特性.本文尝试利用数值方法对多分量感应测井仪器在复杂模型下的响应进行数值模拟，以便对测量得到的视电导率进行有效的校正和反演，从而推动该仪器在固体矿床测井评价中的应用.

2基本原理

在各向异性的导电介质中，电场E和磁场H所满足的微分Maxwell方程为

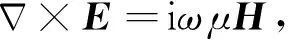
(1)

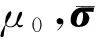
(2)

求解方程(2)相对于求解方程(1)的优点是其有较少的变量，从而有限元离散得到的自由度较小(da Silva et al.,2012).由于感应测井的频率比较低，位移电流可以被忽略不计.为了提高计算效率和避免直接用网格离散源所带来的困难，本文将总场分解成背景场和散射场(Newman and Alumbaugh,1995；王健等,2015).这样(2)式中的源可以由一系列已知的背景场Eb替代.定义散射场Es和异常电导率张量如下：

E=Eb+Es,

(3)

将式(3)代入式(2)中，可得到关于散射场满足的方程为

(4)

在柱坐标系下，有限尺寸的载流线圈源在电导率为σb的各向同性均匀介质中形成的背景场为

×J1(λac)J1(λρ)λdλ，

(5)

(6)

一般来说，求解域的范围取4～5个趋肤深度就可满足要求，趋肤深度由模型中的最小电导率决定.由于四面体网格能更好地处理复杂边界，本文采用开源软件NETGEN(Schöberl，1997)生成非结构化的四面体网格进行空间离散.

通过有限元分析(附录A)将计算得到的单元矩阵Ke，Fe和Ge分别组成矩阵A和右端项b，其中矩阵A是复对称稀疏矩阵，

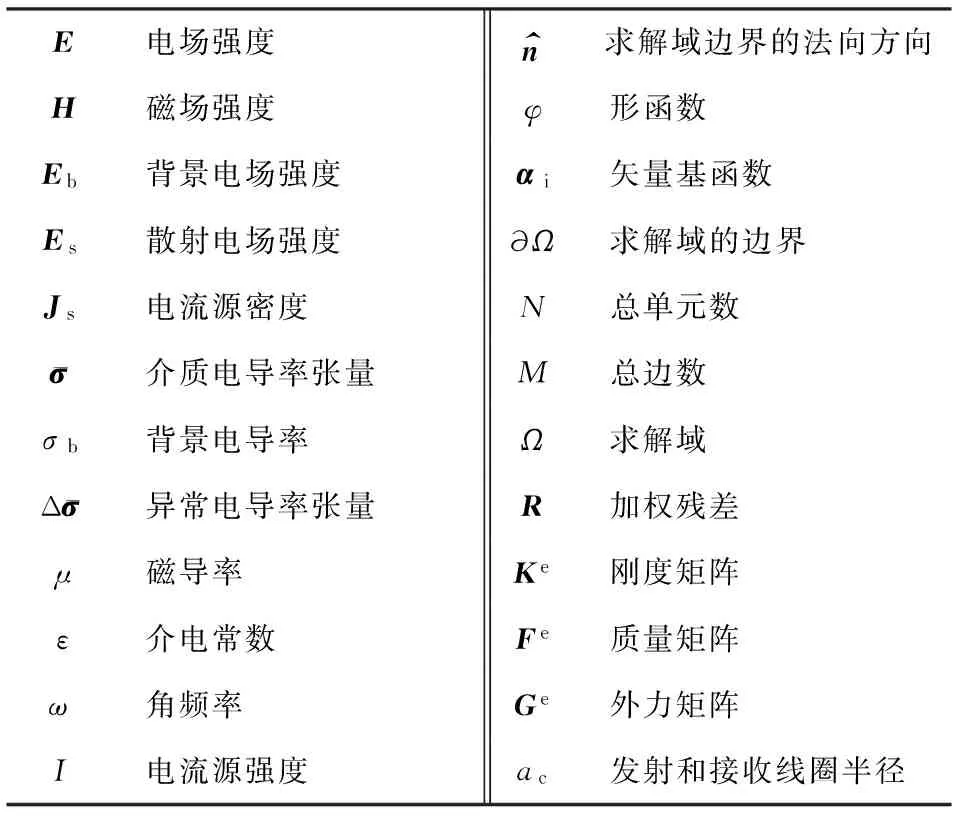
表1　数学符号

Ax=L Ux=b，

(7)

(7)式中L和U是下和上三角矩阵.一旦L和U已经计算得到，那么对于任意的右端项b，可以用下式求得x，

(8)

其中y=L-1b.

求解时LU分解所花费的时间要远高于计算式(8)所需要的时间.在感应测井问题中A矩阵只与网格有关，b矩阵与源相关.因此当仪器沿井轴移动时，如果只进行一次网格剖分，则可以只进行一次LU分解并利用(8)式实现多个测量点响应的快速计算.但是值得注意的是：为了满足边界条件并保证数值精度，需要网格范围取的较大，并且需要对仪器轨迹上的网格进行加密.考虑到LU分解对计算机的内存需求较大，我们设定一个自由度的阈值，当自由度超过阈值时，测量点就被分成Ns组，每组进行一次网格剖分.这样既尽可能减少网格剖分次数并利用LU求解的特点，同时又节省了内存.本文使用多线程并行求解器UMFPACK(Davis,2004)求解线性方程组.

3精度验证

为了验证算法的精度，本文采用具有解析结果的三层模型.将开发的有限元程序对双线圈仪器计算的结果与解析结果进行对比，三层地层的电导率分别为1 S·m-1，0.002 S·m-1，20 S·m-1，中间层厚2 m.发射源电流强度等于1 A，频率为20 kHz.发射线圈半径和源距分别为0.03 m和1 m.模型中感应电流在电导率最低的介质中的趋肤深度δ≈80 m.因而将模型区域设定为一个半径和高分别为398 m和896 m的圆柱.最终网格的总节点数为64212，四面体单元总数为360128，相应的自由度为429156.模拟的结果如图1所示.有限元模拟的结果与解析结果吻合较好：最大误差小于2%.模型中电导率对比度高达104，这说明本文的算法有能力处理实际问题中出现的高电导率对比度的情况.文中所使用的计算机配置为4核3.1 GHz的i5-2400 CPU，内存12G，每个深度点平均计算耗时2.8 s.

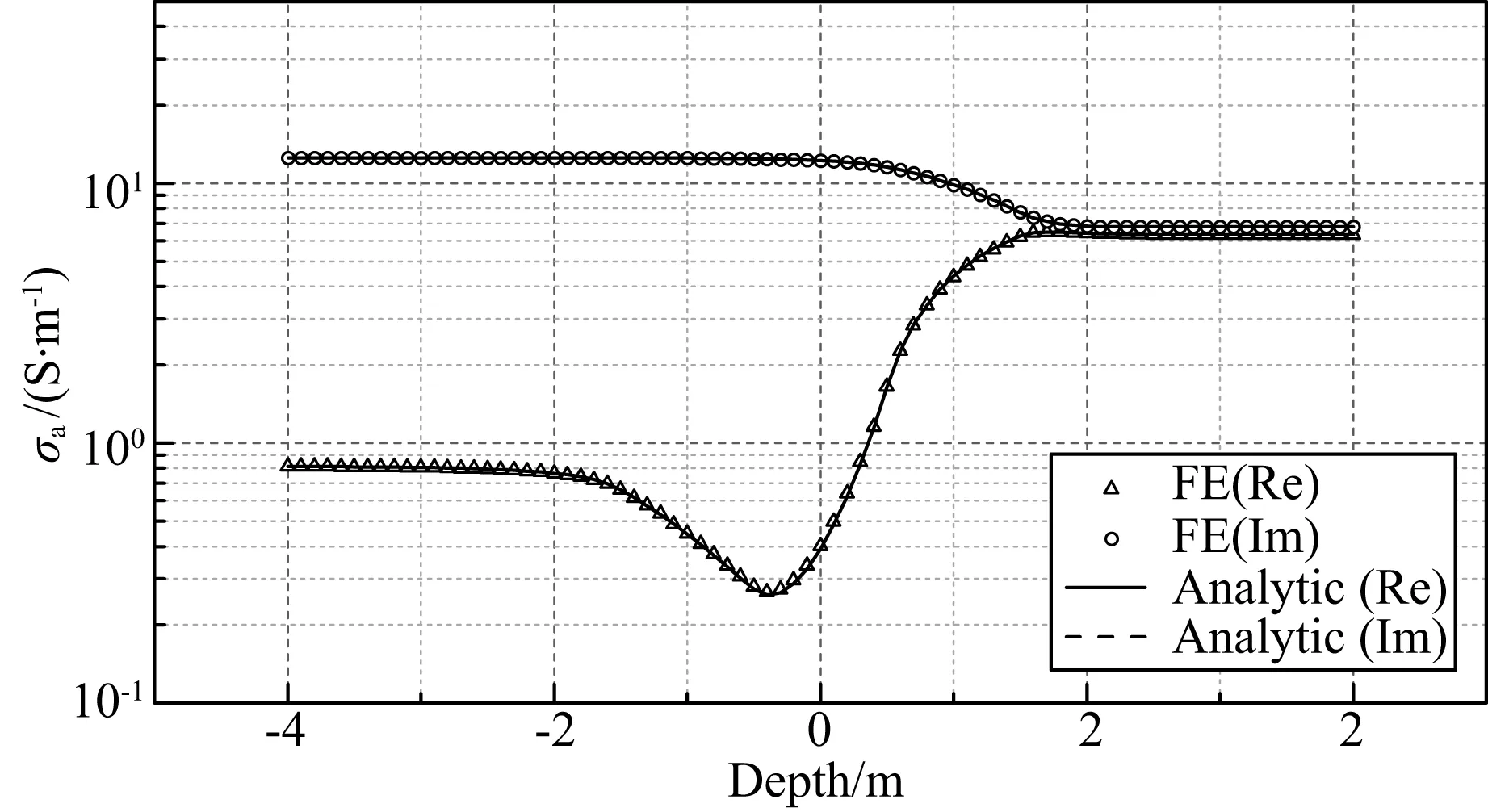
图1　水平三层地层模型的有限元法与解析结果对比

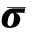
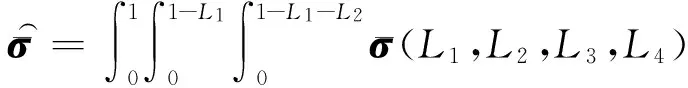
(9)

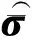
图2是采用均质网格和非均质网格进行模型离散的网格截面图.图2a由于采用均质网格，井眼内的网格尺寸受到井壁的限制而不能扩大，在距离源较远的区域产生了大量不必要的小尺寸单元;图2b中由于采用非均质网格，网格尺寸能够迅速增大，减少了总的单元数量.同时，这种方法也能够保证结果的精度.当井内外介质电导率对比度增大时，一般可以通过增加积分点来提高精度.图3中我们将采用非均匀介质网格的有限元计算的结果与解析结果在1D径向分层地层上进行对比.其中泥浆电导率为0.005S·m-1，井外地层电导率是0.01～50S·m-1的对数等间隔插值，仪器结构与上例相同.程序采用45点Gauss-Legendre积分计算非均匀质单元的平均电导率.从图中可以看到：模拟的结果与解析结果吻合很好，证实了这种处理井眼的方法在井内外电导率对比度高达104时仍然可取得令人满意的精度.

为了验证本文的有限元算法和程序在各向异性介质中的正确性，我们比较了用有限元方法和格林函数法计算的多分量仪器在三层各向异性地层(SunandNie,2008)模型中的响应.地层的参数详见图4a.图4b的结果表明，由有限元计算的水平电导率和垂直电导率与格林函数法计算的十分吻合.

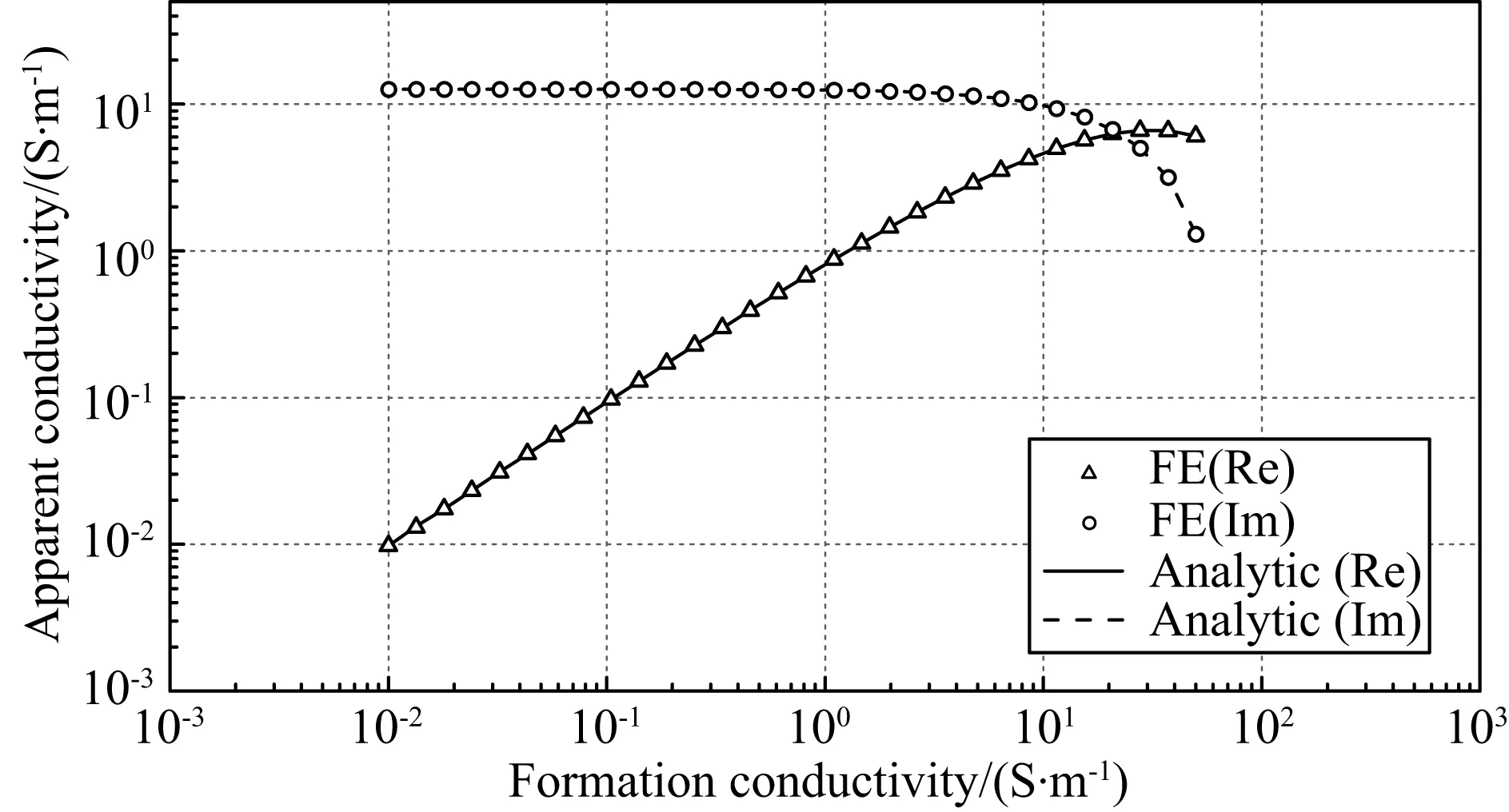
图3　径向分层地层模型的有限元法与解析结果对比

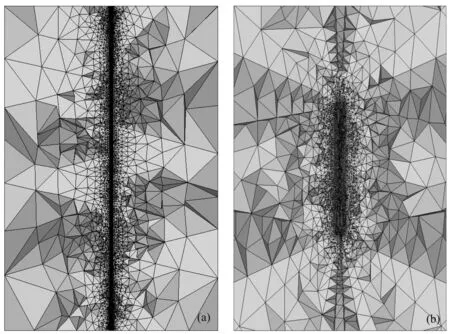
图2　感应测井网格切面图. (a) 均质网格； (b) 非均质网格

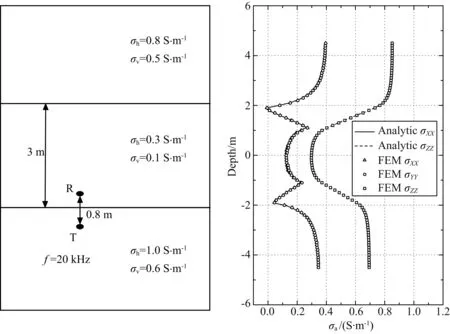
图4　各向异性模型验证. (a)三层各向异性模型; (b)结果对比

4实例分析

4.1倾斜各向异性地层模型

(10)

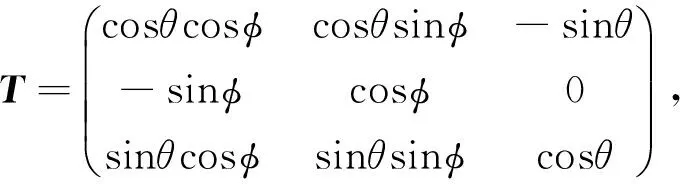
(11)

其中T为转动矩阵，θ为绕Y轴的地层倾角，φ为绕Z轴的地层方位角.

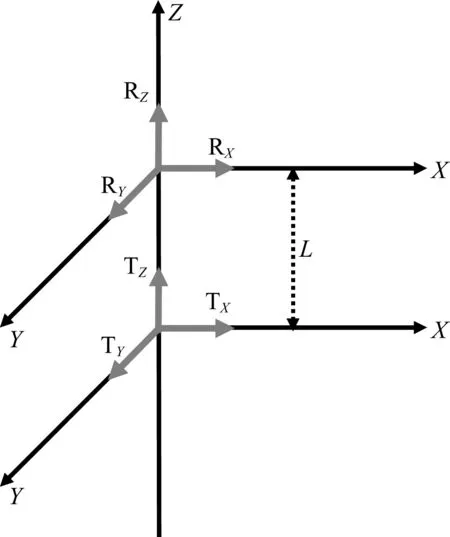
图5　多分量感应测井仪器的基本结构等效图

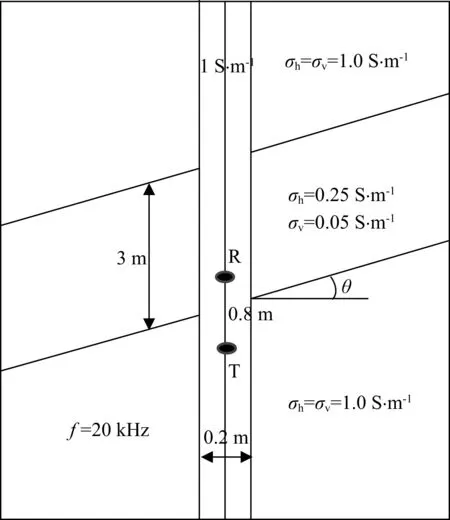
图6　倾斜各向异性地层模型

图7　均匀各向异性倾斜地层的XZ分量和ZX分量

图7给出了在均匀各向异性地层中θ=60°和-60°的XZ和ZX分量，当不存在界面时，XZ分量和ZX分量相等，且θ=60°时有负的幅度，而θ=-60°有正的幅度.图8a—8c分别给出了倾角θ=0°，60°和-60°时9个分量的视电导率曲线.θ=0°时只有共面的XX，YY和共轴的ZZ分量不为0，其余6个分量均为0，XX分量和YY分量相等.在围岩的各向同性地层中，XX和YY分量小于ZZ分量说明共面的XX，YY分量受趋肤效应影响更大.当θ=60°和-60°时，各向异性目标层的XZ分量和ZX分量不等于0，XX分量和YY分量开始分离，并和ZZ分量接近.图8d给出了θ=60°时且目标层电导率为0.25 S·m-1的各向同性地层的9个分量的视电导率曲线.与相同角度的各向异性地层比较，我们可以看到：XZ分量和ZX分量仅在界面附近存在非0的极化角且其方向和各向异性地层相同，这说明极化角的方向与是否存在各向异性无关，而只与地层的倾斜角度以及边界两侧介质电导率的大小有关.当地层正倾斜(0°<θ<90°)时，仪器从低阻地层进入高阻地层时XZ分量的极化角方向为正.当仪器从高阻地层进入低阻地层时，极化角方向为负且其幅度要小于正向幅度.当地层负倾斜(-90°<θ<0°)时，仪器从低阻地层进入高阻地层XZ分量的极化角方向为负.当仪器从高阻地层进入低阻地层时，极化角方向为正且其幅度要小于负向幅度.ZX曲线的规律恰好和XZ曲线的相反.

4.2球形矿体模型

图10是本文计算的球形矿体模型，其中各向同性的球形矿体半径为2 m，球心距离井轴2.6 m，矿体的电导率为5 S·m-1，周围地层电导率为0.05 S·m-1.仪器X方向发射线圈的法向方向与矿体的相对角度φ从0°变化到360°.仪器固定在Z轴上且没有穿过矿体，其线圈系中点平行于矿体球心.图11给出了仪器在此模型下响应的9个分量，在极坐标下清晰地展示了各个分量所具有的周期性.当矿体的方位从0°到360°变化时，常规仪器得到的ZZ分量视电导率曲线呈圆形，因此其不具备方位识别的能力，而且当仪器没有穿过矿体时，感应电流串联地通过地层和矿体，因此其值接近于在均匀地层中的响应，不能反映出矿体的存在.共面的XX分量和YY分量具有一定的方位敏感性，具有180°的周期.XY分量和YX分量也具有180°周期，其与XX分量和YY分量的区别是它们的幅度存在正负变化，在45°和225°取得极大值，在135°和315°取得极小值，在0°，90°，180°，270°不存在XY和YX分量.显然，由于具有180°的对称性，无论如何组合上述4个分量，都无法确定矿体的方位.如图所示，XZ，YZ，ZX，ZY这四个交叉分量具有360°周期，且他们的极大值或极小值总是对应着矿体的方位或者相反的方位.XZ和ZX与YZ和ZY有90°相位差，因此利用(XZ，YZ)或者是(ZX，ZY)可以唯一确定矿体与井的相对位置.如果仪器是旋转测量的，那么仅仅依靠ZX或者XZ分量的信息就能充分地判断矿体的方位.

由于多分量感应测井响应的复杂性，对其测量得到的视电导率曲线的直观解释十分困难.一种利用分量XZ-ZX和XZ+ZX以分离各向异性和边界影响的方法被提出(Omeragic et al.,2006;Davydycheva,2010)，以减少多分量感应测井曲线解释的复杂性.本文将该方法用于计算球形矿体的方位角中，计算方法如下式所示：

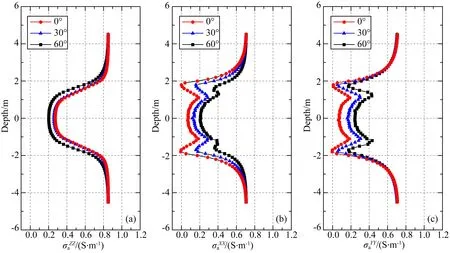
图9　不同地层倾斜角度的视电导率曲线

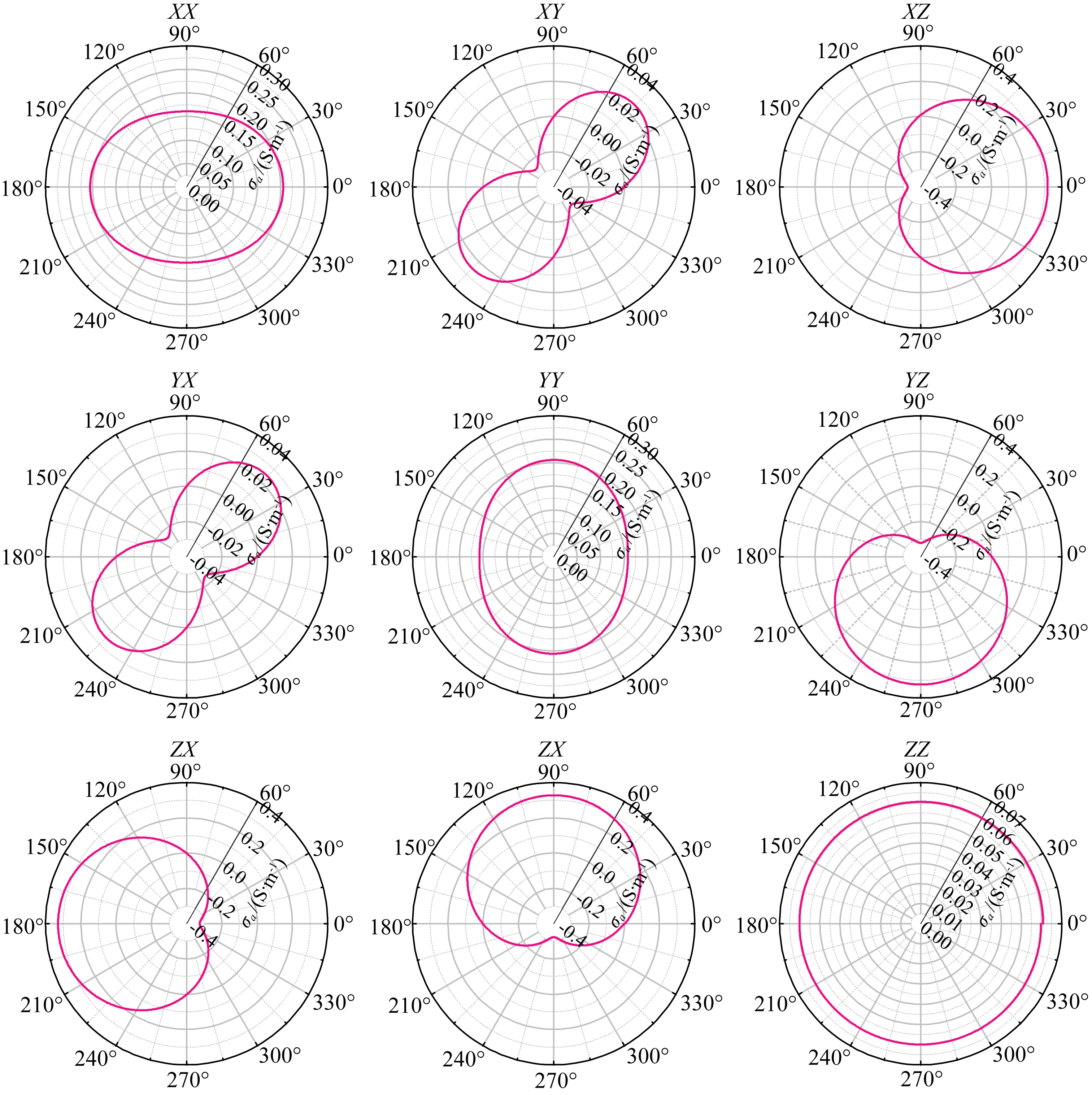
图11　多分量感应测井在球形矿体模型中的响应

(12)

如图12所示，纵坐标是通过式(12)计算得到的方位角，横坐标是实际的方位角.计算的结果和实际的方位角吻合得很好，说明利用交叉分量计算矿体的方位角是可行的.尽管反正切变换的角度不能超过90°，但是根据(YZ-ZY)和(XZ-ZX)的符号可以很容易确定其所在的象限.

图10　球形矿体模型

4.3倾斜圆柱形矿体模型

图13是本文计算的倾斜矿体模型，其中各向同性的圆柱型矿体的长度为6 m，半径1.5 m，倾斜角度θ=45°，矿体电导率为1 S·m-1，周围地层电导率为0.05 S·m-1.仪器X方向发射线圈的法向方向与矿体的相对角度φ从0°变化到360°.仪器沿平分矿体的Z轴正方向移动.图14给出了仪器在此模型下测量得到的9个分量，其中ZZ分量提供了矿体的深度信息，在中间位置出现了高视电导率层，厚度约为3 m，反映出圆柱型矿体半径的大小.但ZZ分量从0°到360°没有任何变化，因此无法判断矿体走向等信息.XX和YY分量也反映了矿体的存在，但与ZZ分量相比所反映的视厚度更小，在矿体长度的边缘位置呈现出极化角.XY和YX分量的幅值只在矿体的边缘才出现明显的周期正负变化.这是因为当仪器处于矿体中时，矿体的走向对XY和YX分量影响不明显.XZ，YZ，ZX，ZY具有360°周期，它们的极大值或极小值总是对应着矿体的走向或者正交方向，因此利用(XZ，YZ)或者是(ZX，ZY)可以唯一确定矿体的走向.我们注意到：XZ和ZX分量在矿体的上和下是不对称的，同时彼此是反对称的，因此可以依靠XZ或者ZX分量确定某一深度点仪器是在矿体之上或者之下，以及矿体的倾斜方向.上述二个例子说明利用多分量感应测井仪器的交叉分量可以获得矿体的方位和走向等信息.当然利用ZX，XZ，ZY，YZ分量判断矿体的方位和走向的前提条件是仪器具有合适的探测深度和分辨率.

5结论

本文在频率域内实现了基于非结构化四面体网格的三维矢量有限元方法的多分量感应测井响应模拟算法，并模拟了多分量感应测井仪器在矿床测井模型中的响应.为了提高计算效率，算法在井眼边界采用非均质网格并利用Gauss-Legendre积分计算四面体单元的平均电导率.同时结合感应测井模型和LU分解方法的特点，实现了一次网格划分多深度点的数值计算.通过三个算例，验证了算法在各向同性介质和各向异性介质中有很好的计算精度和速度.

数值结果表明，多分量感应测井仪器能够识别矿体的各向异性.在水平地层情况下，其ZZ分量能够给出水平电导率，XX和YY分量给出垂直电导率.对于仪器探测深度范围内的有限尺寸矿体模型，由于XZ，YZ，ZX，ZY分量具有360°的方位敏感性，因而能够提供矿体的方位和走向等信息.

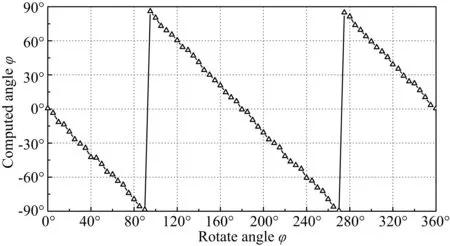
图12　球形矿体方位角计算

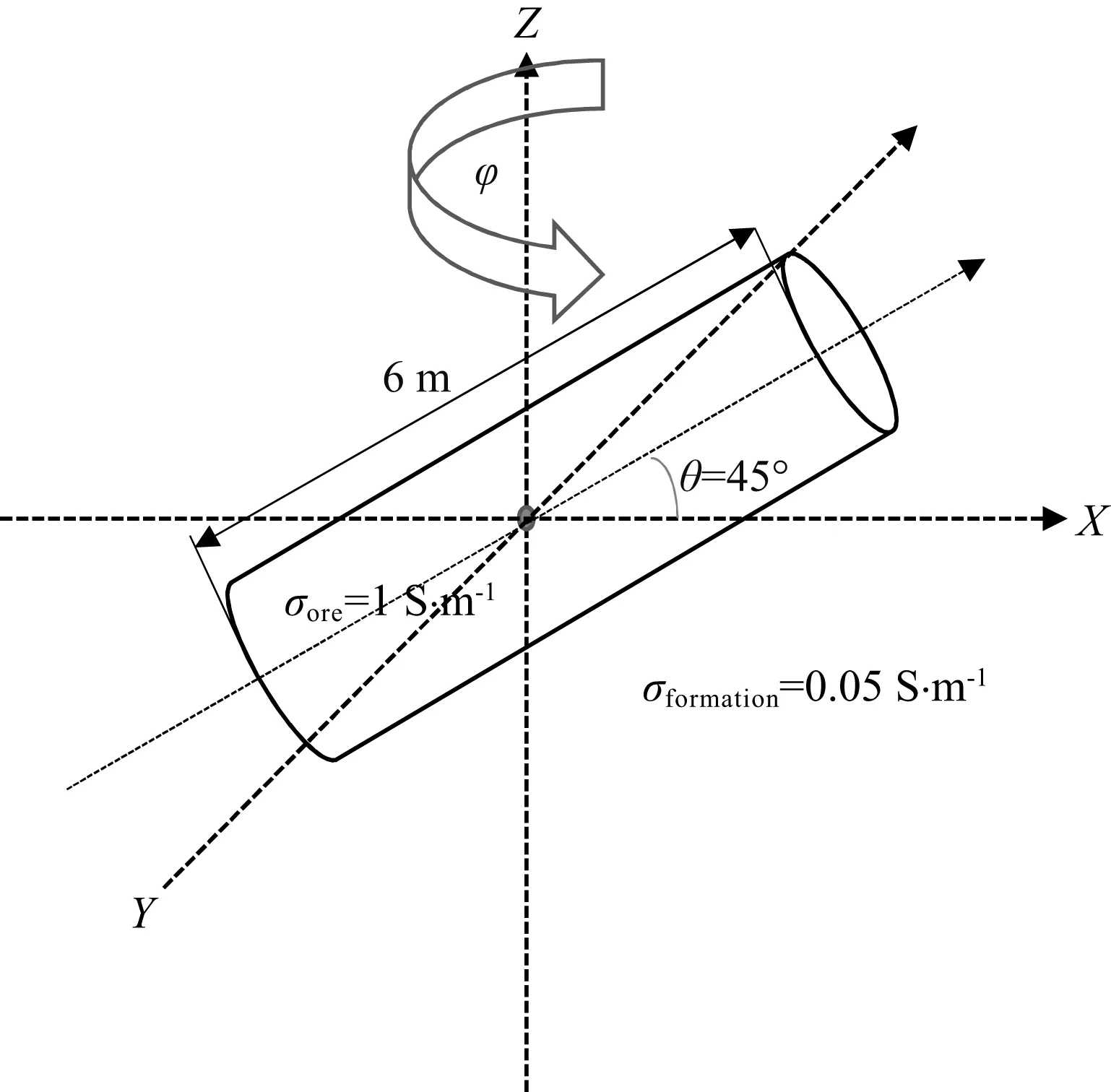
图13　倾斜圆柱型矿体模型

附录A矢量基函数和有限元分析

四面体单元内的节点和棱边的关系如图A1和表A1所示.对于一个四个顶点分别为(a，b，c，d)的四面体单元，其形函数φa(ra)有如下定义(SilvesterandFerrari,1996)：

图A1　四面体单元

图14　多分量感应测井仪器在倾斜圆柱形矿体(θ=45°)模型中的响应

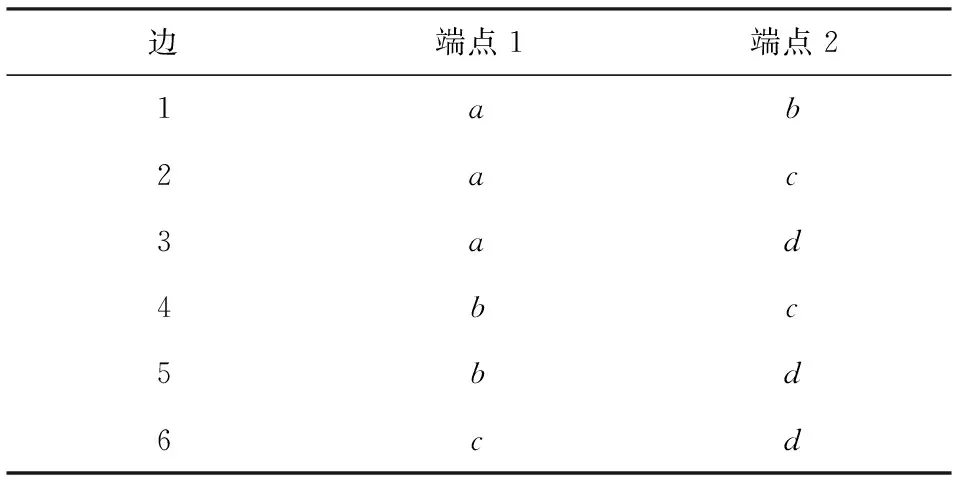
边端点1端点21ab2ac3ad4bc5bd6cd

(A1)

(A1)式中r表示四面体中任一点的位置，其他顶点的形函数有相似的定义.基于矢量有限元，散射场Es可表示为

(A2)

其中ai是待确定的系数，αi(r)是矢量基函数并有如下形式：

(A3)

参数(a，b)是网格中第i条边的始末端点.应用伽辽金方法(ZienkiewiczandTaylor,2005)，并令αj为试函数，则得到方程(4)的弱解形式：

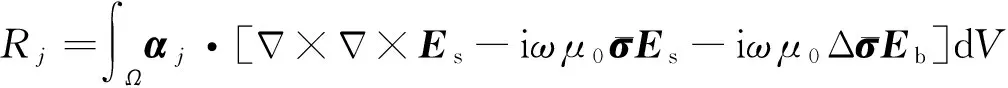
(A4)

方程(A4)可进一步展开：

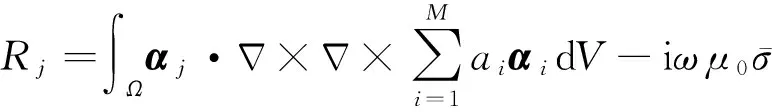
(A5)

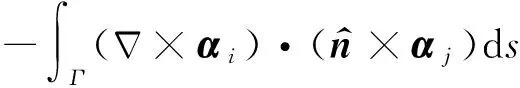
(A6)

(A7)

其有离散形式如下：

(A8)

在得到了网格边上的散射场值后，需要将其转换为节点上的散射场值.如果端点为(a，b)的棱边属于总计P个四面体，并且端点a被D条边共用，则节点a上的散射场可表示为

(A9)

有关后处理方法更详细的讨论参见文献(MukherjeeandEverett,2011).

References

Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 2002. Three-dimensional induction logging problems, Part I: An integral equation solution and model comparisons.Geophysics, 67(2): 413-426.

Badea E A, Everett M E, Newman G A, et al.2001. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials.Geophysics, 66(3): 786-799.

Baltosser R W, Lawrence H W. 1970.Application of well logging techniques in metallic mineral mining.Geophysics, 35(1): 143-152.

Biro O, Preis K. 1989. On the use of the magnetic vector potential in the finite-element analysis of three-dimensional eddy currents.IEEETransactionsonMagnetics,25(4): 3145-3159.Broding R A, Zimmerman C W, Somers E V, et al. 1952. Magnetic well logging.Geophysics, 17(1): 1-26.

Chang S K, Anderson B. 1984. Simulation of induction logging by the finite-element method.Geophysics, 49(11): 1943-1958.

Cheryauka A B, Sato M. 2002. Directional induction logging for evaluating layered magnetic formations.Geophysics, 67(2): 427-437.

da Silva N V, Morgan J V, MacGregor L, et al. 2012. A finite element multifrontal method for 3D CSEM modeling in the frequency domain.Geophysics, 77(2): E101-E115.Davis T A. 2004. Algorithm 832: UMFPACK V4.3—an unsymmetric-pattern multifrontal method.ACMTransactionsonMathematicalSoftware(TOMS), 30(2): 196-199.Davydycheva S, Homan D, Minerbo G. 2009.Triaxial induction tool with electrode sleeve: FD modeling in 3D geometries.JournalofAppliedGeophysics, 67(1): 98-108.

Davydycheva S. 2010. Separation of azimuthal effects for new-generation resistivity logging tools—Part I.Geophysics, 75(1):E31-E40.

Doll H G. 1949. Introduction to induction logging and application to logging of wells drilled with oil base mud.JournalofPetroleumTechnology, 1(6): 148-162.

Druskin V L, Knizhnerman L A, Lee P. 1999. New spectral Lanczos decomposition method for induction modeling in arbitrary 3-D geometry.Geophysics, 64(3): 701-706. Fang S, Gao G, Torres-Verdín C. 2006. Efficient 3D electromagnetic modelling in the presence of anisotropic conductive media, using integral equations.ExplorationGeophysics, 37(3): 239-244.

Guptasarma D, Singh B. 1997. New digital linear filters for Hankel J0 and J1 transforms.GeophysicalProspecting, 45(5): 745-762.

Jin J M. 2002. The Finite Element Method in Electromagnetics. New York: Wiley.

Kennedy D, Peksen E, Zhdanov M. 2001. Foundations of tensor induction well-logging.Petrophysics, 42(6):588-610.

Key K, Ovall J. 2011. A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling.GeophysicalJournalInternational, 186(1): 137-154.Kriegshauser B, Fanini O, Forgang S, et al. 2000. A new multicomponent induction logging tool to resolve anisotropic formations. ∥ SPWLA 41st Annual Logging Symposium. Dallas,Texas.

Li J H, Zhu Z Q, Liu S C, et al. 2011. 3D numerical simulation for the transient electromagnetic field excited by the central loop based on the vector finite-element method.JournalofGeophysicsandEngineering, 8(4): 560-567.Moran J H, Kunz K S. 1962. Basic theory of induction logging and application to study of two-coil sondes.Geophysics, 27(6): 829-858.Mukherjee S, Everett M E. 2011. 3D controlled-source electromagnetic edge-based finite element modeling of conductive and permeable heterogeneities.Geophysics, 76(4): F215-F226.Nédélec J C. 1980. Mixed finite elements in3.NumerischeMathematik, 35(3): 315-341.

Newman G A, Alumbaugh D L. 1995.Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences.GeophysicalProspecting, 43(8): 1021-1042.

Omeragic D, Dumont A, Esmersoy C, et al. 2006. Sensitivities of directional electromagnetic measurements for well placement and formation evaluation while drilling. ∥ 76th SEG Annual Meeting. New Orleans, LA.

Puzyrev V, Koldan J, de la Puente J, et al. 2013.A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling.GeophysicalJournalInternational, 193(2):678-693.Rabinovich M, Tabarovsky L, Corley B, et al. 2006. Processing multi-component induction data for formation dips and anisotropy.Petrophysics, 47(6): 506-526.

Rathod H T, Venkatesudu B, Nagaraja K V, et al. 2007. Gauss Legendre-Gauss Jacobi quadrature rules over a tetrahedral region.AppliedMathematicsandComputation, 190(1): 186-194.

Schöberl J. 1997. NETGEN An advancing front 2D/3D-mesh generator based on abstract rules.ComputingandVisualizationinScience, 1(1): 41-52.Silvester P P, Ferrari R L.1996. Finite Elements for Electrical Engineers. 3rd ed. Cambridge:Cambridgeuniversity Press.

Sun X Y, Nie Z P. 2008. Vector finite element analysis of multicomponent induction response in anisotropic formations.ProgressinElectromagneticsResearch, 81:21-39.

Sun X Y, Nie Z P, Zhao Y W, et al. 2008.The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method.ChineseJ.Geophys. (in Chinese), 51(5): 1600-1607.

Teng J W, Yang L Q, Yao J Q, et al. 2007. Deep discover ore、exploration and exploitation for metal mineral resources and its deep dynamical process of formation.ProgressinGeophysics(in Chinese), 22(2):317-334.

Wang H N,Tao H G, Yao J J, et al. 2008. Study on the response of a multicomponent induction logging tool in deviated and layered

anisotropic formations by using numerical mode matching method.ChineseJ.Geophys. (in Chinese), 51(5):1591-1599.Wang H M, Wu P, Rosthal R, et al. 2008. Modeling and understanding the triaxial induction logging in borehole environment with dip anisotropic formation. ∥ 2008 SEG Annual Meeting, Society of Exploration Geophysicists.309-313

Wang J, Chen H, Wang X M, et al. 2015. Research on selection method of background field for finite element simulation of induction logging.ChineseJ.Geophys. (in Chinese),58(6): 2177-2187.

Wei B J, Wang T T, Wang Y. 2009. Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Green′s function.ChineseJ.Geophys. (in Chinese),52(11): 2920-2928.Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth.Geophysics, 67(4): 1104-1114.Weiss C J. 2013. Project APhiD: A Lorenz-gauged A-Φ decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth.Computers&Geosciences, 58: 40-52.

Xiao J Q, Zhang G Y, Hong D C, et al .2013.Fast forward modeling and data processing of 3D induction logging tool in layered anisotropic formation.ChineseJ.Geophys. (in Chinese),56(2): 696-706.Zienkiewicz O C, Taylor R L. 2005. The Finite Element Method for Solid and Structural Mechanics. Oxford: Butterworth-H.

附中文参考文献

孙向阳, 聂在平, 赵延文等. 2008. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报, 51(5):1600-1607.

滕吉文，杨立强，姚敬全等. 2007. 金属矿产资源的深部找矿，勘探与成矿的深层动力过程.地球物理学进展，22(2):317-334.

汪宏年, 陶宏根, 姚敬金等. 2008. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报, 51(5):1591-1599.

王健, 陈浩, 王秀明等. 2015. 有限元感应测井模拟的背景场选择方法研究. 地球物理学报, 58(6):2177-2187.

魏宝君, 王甜甜,王颖. 2009. 用磁流源并矢 Green 函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应. 地球物理学报, 52(11):2920-2928.

肖加奇, 张国艳, 洪德成等. 2013. 层状各向异性地层中三维感应测井响应快速计算及资料处理. 地球物理学报, 56(2):696-706.

(本文编辑胡素芳)

基金项目国家重大科研装备研制项目“深部资源探测核心装备研发”(ZDYZ2012-1-07)资助.

作者简介王健，男，1987年生，博士生，主要从事电磁波场数值模拟研究. E-mail: wangjianshinian@163.com

doi:10.6038/cjg20160130 中图分类号P631

收稿日期2015-02-16，2015-10-22收修定稿

Response modeling of multi-component induction logging tool in the mineral logging using vector finite element

WANG Jian1,2， CHEN Hao1, WANG Xiu-Ming1

1StateKeyLaboratoryofAcoustics,InstituteofAcoustics,ChineseAcademyofSciences,Beijing100190，China2UniversityofChineseAcademyofSciences,Beijing100049，China

AbstractWith the development of economy, the shallow resources have been exploited excessively, the deep-seated resources become the investigation targets for the geophysics. Borehole geophysics become more important due to the reduction of resolution and accuracy of the surface methods, and the increase of the cost for drilling and sampling. So how to realize fine evaluation of solid deposit by logging is a crucial problem. This article′s main objective is to determine the relative position of solid mineral deposit and well based on the numerical simulation of multicomponent induction logging method.

KeywordsEdge finite element；Multi-component induction logging；Solid mineral deposit

王健, 陈浩, 王秀明. 2016. 用于固体矿床多分量感应测井响应模拟的矢量有限元法.地球物理学报，59(1):355-367,doi:10.6038/cjg20160130.

Wang J, Chen H, Wang X M. 2016. Response modeling of multi-component induction logging tool in the mineral logging using vector finite element.ChineseJ.Geophys. (in Chinese),59(1):355-367,doi:10.6038/cjg20160130.