门电压对并联非对称耦合双量子点系统输运性质影响
廖艳华,水 开
(湖北理工学院 数理学院, 湖北 黄石 435003)
门电压对并联非对称耦合双量子点系统输运性质影响
廖艳华,水开
(湖北理工学院 数理学院, 湖北 黄石 435003)
摘要:采用数值重整化群方法,研究了与导线并联非对称耦合的双量子点系统的输运性质。研究表明:通过改变与导线强耦合的量子点1(QD1)的能级,就能改变量子点中电子的占有数,影响系统的输运性质;且当导线与量子点2(QD2))间弱耦合强度较弱时,系统电导随着与导线强耦合的量子点的能量增加而呈现单调减小;但随着弱耦合强度的增加,系统电导随着强耦合量子点的能级增加会出现先减小后增加的凹槽形。
关键词:数值重整化群;强关联系统;量子点;门电压
量子点设备是研究诸如近藤效应、量子相变等多体现象非常有效的工具,也为我们在实验室中对近藤效应的操控提供了新的可能。Cronenwett等人[1-2]报道了低温环境下在量子点设备中观察到近藤效应, 这再次激起人们新一轮的研究近藤效应的热潮[3-4]。由于电子结构能决定原子的自旋,所以很难改变原子中电子的自旋方向,但却能够很容易地改变量子点的自旋。譬如,量子点中的能级谱线能够很容易地被磁场所改变,如用强度为1 T的磁场就能使量子点从自旋单态转变为自旋三重态,而如果要使真正的原子发生自旋状态的改变,就需要106T的磁场,而在实验室里是不可能产生这么大的磁场,所以,采用量子点结构来研究近藤效应具有其他人工微结构都无法企及的优势。到目前为止,已有很多方法在量子点中调控近藤效应方面做出了努力,如较为常见的是通过调节外端控制量子点参数的“旋钮”,就能对量子点离散的能级进行改变,以此方式来改变量子点内电子的化学势,从而达到改变量子点中电子数的目的。就安德森模型中的参数而言,在试验中能改变量子点的能级大小()、量子点与导线间的耦合强度(Γ)、量子点中能级间的库伦排斥势(U)的外部“旋钮”是门电压,量子点的这些参数都能非常简单的通过调控门电压的方式进行改变。所以,能让量子点系统中存在奇数个自旋大小为1/2的电子,以此种方式来模拟铜中掺杂钴的系统在低温下产生近藤效应。
通过调节门电压和磁场的方式,Silva等人对侧耦合双量子点模型中的自旋极化输运性质进行了研究[5],发现线性电导被完全自旋极化,该现象为高度可调的自旋过滤器设备的研制提供了广阔的应用前景。尽管如此,门电压对并联非对称耦合双量子点系统中自旋输运的影响鲜有人提及。在本文中,我们将研究双量子点系统几何结构装置,研究与导线非对称耦合的双量子点中强耦合的量子点(QD1)能级发生改变时,系统的输运性质会受到何种影响。
1数值计算方法
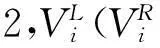

图1 双量子点系统示意图
在本研究中,使用含有两杂质的安德森哈密顿量来描绘并联双量子点系统,其对应的哈密顿量可表示为:
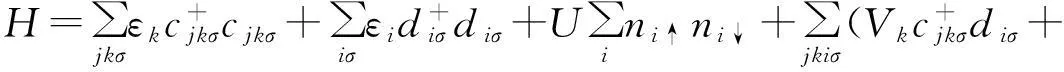
(1)
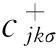
(2)
式(2)中,f(ω)是费米函数,Tσ(ω)指自旋为σ的透射率,且:
(3)
选取费米能εF=0,如此,则在零偏压的极限下,零温的线性电导率为:
Gσ=Tσ(ω=0)e2/h
(4)
态密度表达式为:
(5)
推迟格林函数定义为:
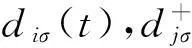
(6)
此外,量子点间自旋关联函数为〈Si·Sj〉,这里Si(Sj)指第i(j)个电子点的自旋算符。
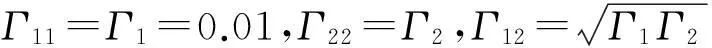
在数值重整化群的计算中,当粒子空穴对称点即εi=-U/2时,量子点中是半满占据;在U/Γ≫1的强关联区域,每个量子点单占据。双量子点间以传导电子为媒介而导致的RKKY互作用会使双量子间形成铁磁关联的自旋三重态。
2ε1受门电压调制时系统的输运性质
2.1非对称耦合双量子点系统的输运性质
系统中粒子的输运性质随量子点1能级的变化情况见图2。图2(a)为量子点中电子占有数n1σ随量子点1能级的变化;图2(b)为自旋关联函数(S1·S2)随量子点1能级的变化;图2(c)与图2(d)分别为系统的电导Gσ和总磁矩μ2(T)随量子点1能量的变化关系。这里,U=0.15,ε2=-0.075,Γ1=0.01。
在图2(a)中,由于ε2=-U/2=-0.075,量子点2处于粒子-空穴对称,所以量子点2中电子的占有数始终为1。随着ε1的增加,量子点1中电子的占有数n1σ会逐渐减少,且减少的速度不受Γ2大小的影响。如图2(b)所示,随着量子点1中电子数的减少,两量子点间的关联逐渐减弱,最后消失,没有反铁磁关联存在。值得指出的是,从图2(c)中可以观察到,当Γ2较小时(如Γ2=0.002),此时系统的电导会随着ε1的增大而单调减小,最后消失。但当Γ2增大时(如Γ2=0.004),电导随ε1的增大不再呈现单调变化,出现凹槽(dip)形。图2(d)所描绘的是系统的总磁矩随ε1的变化情况。当Γ2=0.002,ε1=0.001时,量子点1中不再占有电子,而量子点2中占有一个电子[图2(a)],此时系统总磁矩在低温下仍然为单电子磁矩。此现象说明只有在更低的温度下,导线才能屏蔽与导线弱耦合的量子点中电子,此时总磁矩才会变为零。磁矩的这一规律表明,在Γ2=0.002时系统的电导呈单调变化,这是由于Γ2较小时,导线与量子点之间形成微弱的近藤共振。
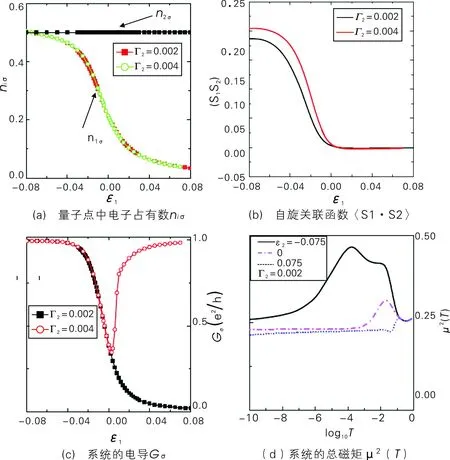
图2 粒子的输运性质随量子点1能级的变化情况
2.2非对称耦合双量子点系统的中电子的态密度
ε1取不同值时量子点1和量子点2的态密度A1σ(ω)、A2σ(ω)见图3。当Γ2=0.002,随着ε1增大,量子点1中的电子占有数减少,所以近藤峰的高度降低。随着ε1的继续增大,量子点1与导线间的近藤效应逐渐减弱后消失。由于占有的电子数减少,整个峰值随着ε1的增大往费米能右边移动[图3(a)]。由于量子点2与导线耦合强度弱,导线与量子点2之间的近藤效应极其微弱[图3(b)]。随着量子点1中的电子占有数的减小(量子点1能量增大),量子点之间的相互关联作用减弱[图3(b)],此时,在量子点2的态密度谱中,已不能观测到近藤峰。当Γ2=0.004,在粒子-空穴对称点在ε1=-U/2附近,如ε1=-0.075,能观察到在费米能处会有近藤峰出现,且在近藤峰附近也会出现RKKY峰 [图3(c)]。这一特征也表明此时出现在谱中的近藤峰应该是双量子点共同效应。随着ε2增加,如ε1=-0.01,量子点1中的近藤峰与RKKY峰消失,取而代之的是出现在费米能附近的库仑峰。随着ε1继续增加,如ε1=0.01,量子点1中已不再占据电子,谱中的近藤峰重现[图3(d)],此时谱中近藤峰旁边已无RKKY峰,说明此时的近藤效应是由导线屏蔽量子点2中电子所产生,与量子点1没有关系。
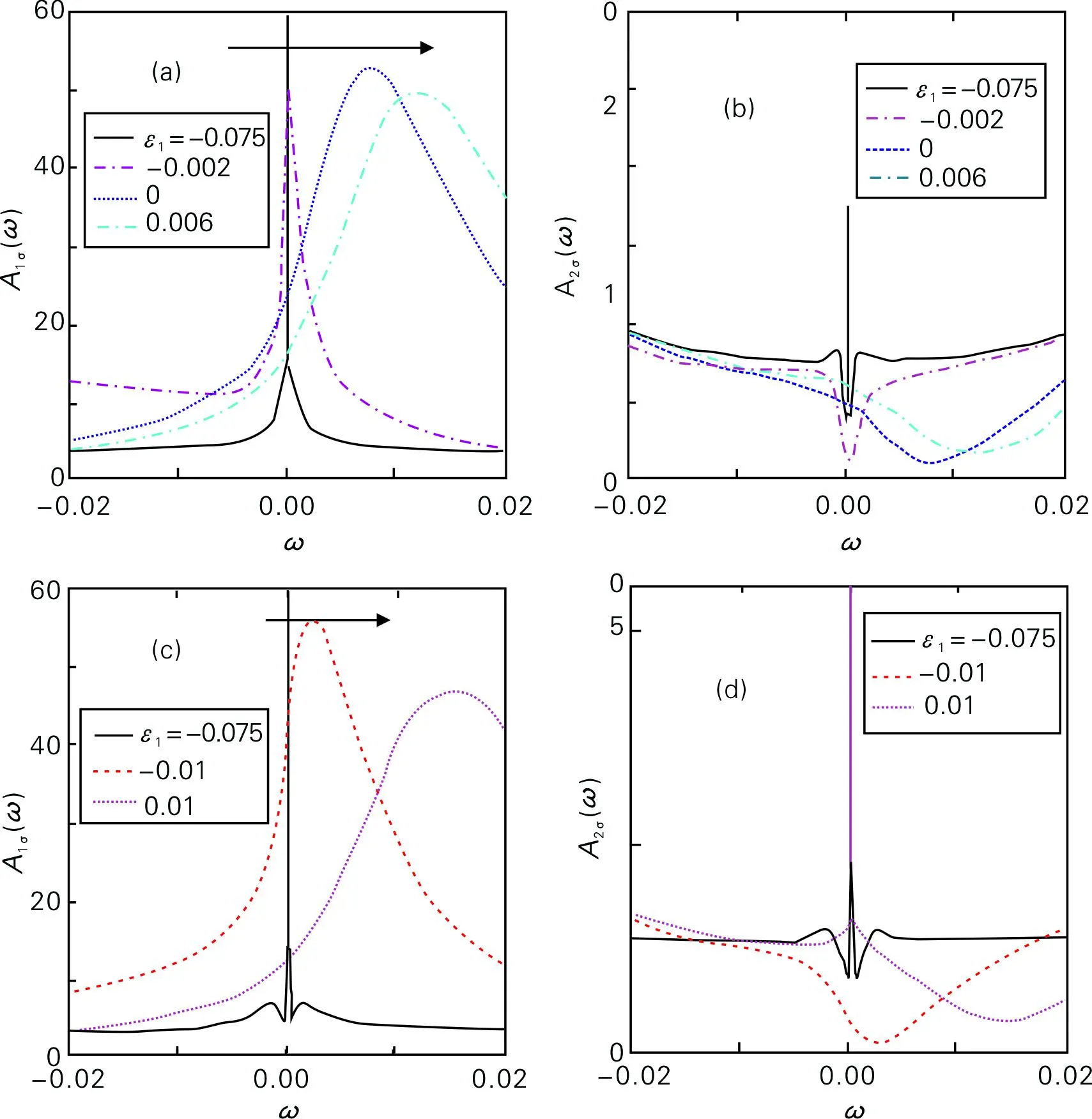
图3 ε1取不同值时量子点1和量子点2的态密度A1σ(ω)、A2σ(ω)
图3(a)与(b)中Γ1=0.01,Γ2=0.002,沿着箭头的方向,ε1依次取值为:-0.075,-0.002,0,0.006。图3(c)与(d)中Γ1=0.01,Γ2=0.004,沿着箭头的方向,ε1依次取值为:-0.075,-0.01,0.01。
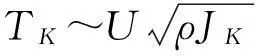
3结论
采用数值重整化群方法,研究了与导线非对称耦合的双量子点系统在调节与强耦合量子点能级时系统的输运性质。研究表明:调节与导线强耦合的量子点(量子点1)的能级ε1,可以对系统的电导进行调控。在量子点2与导线弱耦合的强度(Γ2)较小的条件下,随着ε1的增加,电导呈现单调减小;当Γ2的强度增加时,系统的电导出现凹槽结构。当Γ2较大时,在临近粒子-空穴对称点,近藤效应能使系统电导达到最大。随着ε1的增加,量子点1中电子的占有数减少,近藤效应会受到抑制,此区域对应着电导的凹槽区域[图2(c)]。当ε1远离粒子-空穴对称点时,即当量子点1中空占据时,近藤效应重现,系统电导再次达到极大。电导的这一变化特征也表明在ε1增加过程中发生了自旋三重态到自旋双重态的量子相变。通过对谱的研究,进一步指出,在自旋三重态,近藤效应是由导线与2个量子点共同产生的近藤屏蔽效应,而在自旋双重态所对应的电导极大值是导线与量子点2间产生的近藤屏蔽,与量子点1无关。本研究所获结论旨在为量子器件的设计提供有益帮助。
参 考 文 献
[1]Loss D,DiVicenzo DP. Quantum Computation with Quantum Dots[J].Phys.Rev.A,1997,57(1):120-126.
[2]Goldhabergordon D,Goeres J,Kastner MA,et al.From the kondo regime to the mixed-valence regime in a single-electron transistor[J].Phys. Rev.Lett.,1998,81(23):5225-5228.
[3]Rengstl U,Schwartz M,Herzog T,et al.On-chip beamsplitter operation on single photons from quasi-resonantly excited quantum dots embedded in GaAs rib waveguides[J].Appl.Phys.Lett.,2015,107(7):46-52.
[4]Li T,Lu H,Fu L,et al.Enhanced carrier collection efficiency and reduced quantum state absorption by electron doping in self-assembled quantum dot solar cells[J].Appl.Phys.Lett.,2015,106(5):5014-128.
[5]Silva Da,Luis G G V Dias,Vernek E,et al.Spin-polarized conductance in double quantum dots:Interplay of Kondo,Zeeman,and interference effects[J].Phys.Rev.B,2012,87(20):172-176.
[6]Meir Y,Wingreen NS,Lee PA.Low-temperature transport through a quantum dot:The Anderson model out of equilibrium[J].Phys.Rev.Lett.,1992,70(17):2601-2604.
[7]Wang WZ.Spin filtering and quantum phase transition in double quantum dots attached to spin-polarized leads[J].Nanotechnology,2011,22(20):459-464.
[8]Costi TA.Magnetotransport through a strongly interacting quantum dot[J].Phys.Rev.B,2001,64(24):241310(R)-4.
[9]Misiorny M,Weymann I,Barna J.Interplay of the Kondo effect and spin-polarized transport in magnetic molecules,adatoms,and quantum dots[J].Phys.Rev.Lett.,2011,106(12):126602-4.
[10]Liao YH,Huang J,Wang WZ.Real two-stage Kondo effect in parallel double quantum dot[J].Journal of Magnetism and Magnetic Materials,2015,377:354-361.
(责任编辑吴鸿霞)
收稿日期:2016-03-30
基金项目:湖北理工学院教学改革研究项目(项目编号:2015B09);湖北理工学院实验室开放基金项目。
作者简介:廖艳华,讲师,博士,研究方向:强关联电子系统。
doi:10.3969/j.issn.2095-4565.2016.03.009
中图分类号:O552.6
文献标识码:A
文章编号:2095-4565(2016)03-0042-04
Effect of Gate Voltage on Transport Properties of Asymmetrical-coupled Double Quantum Dots
Liao Yanhua,Shui Kai
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi Hubei 435003)
Abstract:By using the numerical renormalization group method,the transport properties in double quantum dots asymmetrically coupled to leads were studied.The results shows that by tuning the energy level of QD1(∈1)the electron numbers in QD1 can be controlled and transport properties of the system will be influenced.When the weak coupling strength between conductor and Quantum Dots 2(QD2)is relatively weak,with the increase of the energy level of QD1,it is found that the conductance decreases monotonously;However;With the growth of weak coupling strength,the conductance shows a dip structure near ∈1=0.
Key words:numerical renormalization group;strong correlated system;quantum dot;voltage-gated

