海洋温跃层分析方法比较
江伟,邢博,楼伟,连仁明
(海军海洋水文气象中心,北京 100161)
海洋温跃层分析方法比较
江伟,邢博,楼伟,连仁明
(海军海洋水文气象中心,北京 100161)
摘要:比较了垂直梯度法、曲率极值点法和拟阶梯函数法提取温度跃层信息的异同,结果表明:采用曲率极值点法和拟阶梯函数相结合的方法,能够给出较为准确的跃层上下界面位置,即跃层上界选用曲率极值点法和拟阶梯函数法确定跃层上界的最大值,而跃层下界则选用拟阶梯函数的结果。同时利用再分析资料初步诊断分析了西北太平洋冬季、春季、夏季、秋季温度跃层特征信息分布演变特征。
关键词:温跃层;垂直梯度法;曲率极值点法;拟阶梯函数法
1 引言
跃层是海洋中重要的物理现象,针对所研究的物理量不同,海洋中的跃层可分为温度跃层、密度跃层、盐跃层、声跃层等。海洋跃层的空间分布和季节变化与水团垂直边界的划定息息相关。声信号是海洋中重要的通信媒介,声速的铅直分布特征对于水中通讯、水中目标探测具有重要的意义。而海洋密度场结构直接决定着声速剖面,密度跃层是海洋密度结构的重要且典型的分布特征。比较海洋跃层诊断分析方法,研究跃层的深度、厚度和强度及其时空演变特征,对于深入研究海洋跃层的形成和演变机理具有重要的科学意义,同时科学合理诊断分析跃层结构特征,有利于水中通讯、水下目标探测活动的开展,对海洋渔业、海上军事活动具有实际应用价值。
国外研究者早在20世纪60年代就开展了海洋温度结构方面的研究工作,比如Turner等[1]利用室内实验与理论分析相结合的方法研究了季节温跃层的形成和维持,Gill等[2]利用实测资料对季节跃层模型进行了检验,着重分析了动力混合和对流混合对上层温度结构的影响。随着海洋科学的研究不断深入,国外对跃层结构的描述性工作已越来越少,更多的研究转向跃层内的混合过程、跃层结构的长期变化等方面上来。Gregg[3-4],Moum[5]探讨和总结了跃层内的湍流混合,Radko等[6]探讨了中尺度涡致通量在温跃层维持中的作用,McDonagh等[7]研究了南印度洋温跃层的年代际变化。
国内研究者也从观测资料分析、温跃层分析方法、机理研究等方面开展了相关研究。观测资料分析方面,葛人峰等[8]基于CTD资料,采用拟阶梯函数逼近法对黄、东海温度垂直剖面拟合逼近,并对黄海、东海陆架区的温度垂直结构进行了类型划分。张婷婷等[9]利用ATLAS浮标资料分析了南海温跃层的短周期震荡,鲍献文等[10]利用大面调查资料分析了北黄海温盐分布季节变化特征。
针对温跃层分析方法方面,吴巍等[11]基于南海CTD资料和南海Levitus资料,比较了垂向梯度法、S-T法等确定跃层的方法,讨论了深水、浅水等不同情况应该重点考虑的问题。葛人峰等[12]分析中国陆架海区CTD资料发现,陆架区的水文要素垂直结构基本都可理想化为三层垂直结构模式:上均匀层、跃层和下均匀层。随后葛人峰等将最小二乘应
跃层本身的物理含义是指温度等物理量的垂直梯度大的水层,通常跃层之上为混合层,水体温度等物理量较为均匀,跃层之下,温度等物理量变化缓慢。本文将基于跃层的这一基本含义,比较垂直梯度法、曲率极值点法和拟阶梯函数法在提取温度跃层信息方面的异同。
2 跃层分析方法简介
表述温度跃层的物理参量有跃层深度、跃层厚度、跃层中温度梯度等,跃层分析方法有垂向梯度法、S-T法、拟阶梯函数法、最优分割法、曲率极值点分析法、三次样条数值函数分析法等。下面给出了垂向梯度法、S-T法、曲率极值点分析法和拟阶梯函数法的基本思路。
垂直梯度法:根据《海洋调查规范》以及《我国专属经济区和大陆架勘测技术规程》规定的温跃层和密度跃层强度的最低标准值(一般分为深水和浅水两种标准),在深水(水深>200 m),温度梯度值为0.05℃/m,密度梯度值为0.01 kg/m4;在浅水(水深<200 m),温度梯度值为0.2℃/m,密度梯度值为0.1 kg/m4;对温度和密度资料求垂向梯度,将垂直梯度值大于或等于上述最低指标值的水层定为跃层,其上下端点所在深度作为跃层上层深度和下界深度。
S-T法:用海表温度减去0.5℃,确定温跃层上界深度,即温跃层上界深度被定义成比表层温度低0.5℃处的深度,再利用温跃层上界深度处的温度和海表盐度计算密度跃层上界深度处的位密,由此确定密度跃层上界深度。针对跃层下界深度,还需要通过其他方法进行确定。
曲率极值点法:此方法不在《海洋调查规范》规定的范围内,其基本思路是按照跃层的定义,用“曲率极值”点这个量化标准确定跃层界点,即计算温度垂直分布曲线的曲率,利用曲率的极大和极小值确定跃层上、下界点。该方法对于典型的强跃层结构能够给出合理的结果,但是对于阶梯型温度分布,却很难确定跃层上、下界深度。
拟阶梯函数法:根据跃层的定义和温度垂直分布曲线形态,将海水理想划分为上均匀层、跃层和下均匀层三层垂直结构,建立一个类似于阶梯函数的三层垂直结构函数去拟合要素垂直分布曲线,利用最小二乘方法确定拟阶梯函数的待定系数的最佳值,从而根据该拟阶梯函数确定跃层上、下界、跃层强度和跃层厚度。
针对理想温度剖面(见图1a),我们分别利用垂直梯度法(见图1b)、曲率极值点法(见图1c)、拟阶梯函数法(见图1d)诊断跃层,图中给出了各种诊断方法所依据的物理量或假设以及诊断出的跃层上、下界位置。从图中可以看出,垂直梯度法利用温度垂直梯度判别跃层所在位置,曲率极值点法通过曲率的极大值和极小值诊断跃层上下界,而拟阶梯函数法假设跃层具有典型的3层结构。对于典型的上均匀层、跃层、下均匀层的温度垂直结构,3种方法均能合理诊断出跃层特征,虽然不同方法诊断出的上下界位置稍有差异,但差异并不大。实际海洋温盐结构远比图1a所示的理想情况复杂,文中第三部分将选用垂直梯度法、曲率极值点法和拟阶梯函数法,利用数值模式输出数据分析研究海域跃层结构特征,并比较3种方法的异同。
这里还需说明的是,根据《海洋调查规范》以及《我国专属经济区和大陆架勘测技术规程》规定的温跃层强度的最低标准值(一般分为深水和浅水两种标准),在深水(水深>200 m),温度梯度值为0.05℃/m,在浅水(水深<200 m),温度梯度值为0.2℃/m;对温度资料求垂向梯度,将垂直梯度值大于或等于上述最低指标值的水层定为跃层,其上下端点所在深度作为跃层上层深度和下界深度。如果严格使用0.05℃/m和0.2℃/m作为深水和浅水跃层梯度阈值,则会在200 m等深线处出现明显的不连续现象,这里我们将水深介于150 m和300 m之间的区域作为过渡区,在此区域跃层梯度阈值线性的从0.05℃/m变化到0.2℃/m。
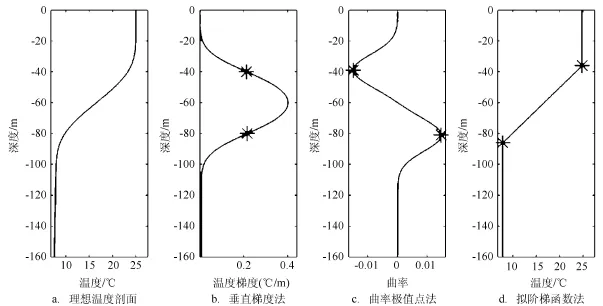
图1 诊断跃层结果示意图(其中黑色星号为诊断出的跃层上界和下界位置)
3 3种分析方法比较分析
使用的数值产品为同化得到的西北太平洋背景场资料,所用模式为POM模式,水平分辨率为(1/8)×(1/8)º,垂向分21层,主要同化数据为ARGO数据,同化方法为集合卡门滤波。通过与Levitus资料等对比分析发现本文所用数值产品能够较好代表西北太平洋气候态温盐场,由于本文重点放在跃层识别与信息提取方法上,因而针对数值产品的检验分析,不再赘述。
图2给出了所选用数值产品覆盖区域及跃层结构分析所选站点(星号),图3给出了10°N断面所选4个站位(经纬度在中间子图上方给出)夏季(8月15日)温度垂直剖面与垂直梯度法、曲率极值点法、拟阶梯函数法所得跃层的上下界面位置。图4给出了30°N断面所选4个站位3种方法所得跃层上下界面位置。从图中可以看出,在跃层结构非常明显的情况下3种方法均能给出较为合理的结果,而且跃层上下界面位置相差不大。同时3种方法各有优缺点,垂直梯度法由于有些剖面温度梯度没有超过阈值而探测不到跃层,但是温度梯度依然是较为明显的;曲率极值点法由于数据中存在的噪声而有时判断错误,同时当出现一强一弱两个跃层时,通常仅能判断出较强的跃层结构,使得跃层厚度数据明显异常,特别是极端情况下,数据中噪声数据使得计算得到的曲率极大和极小值非常接近,从而造成跃层上、下界位置几乎重合,如图3、4所示;拟阶梯函数法,能够较好的判别跃层位置,但是当出现一强一弱两个跃层时,通常也仅能判断出下面的跃层信息。
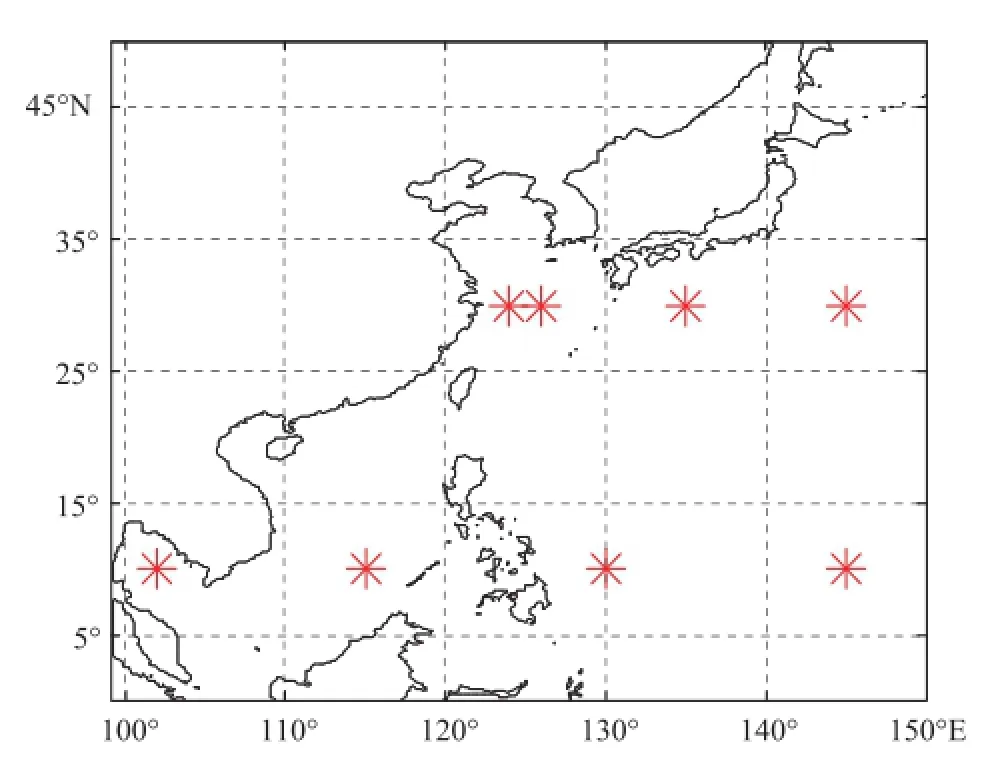
图2所选用数值产品覆盖区域及跃层结构分析所选站点(红色星号)
考虑到跃层本身的物理含义是指温度等物理量的垂直梯度大的水层,垂直梯度法由于先验的给出跃层强度阀值而对于较弱的跃层无法分辨,而曲率极值点法和拟阶梯函数法则是根据温度剖面自身的性质进行判断,无先验阀值带来的问题。综合分析3种方法的优劣,我们认为采用曲率极值点法和拟阶梯函数相结合的方法,能够给出较为准确的跃层上下界面位置,即跃层上界选用曲率极值点法和拟阶梯函数法确定跃层上界的最大值(最靠近海面位置),而跃层下界则选用拟阶梯函数的结果。
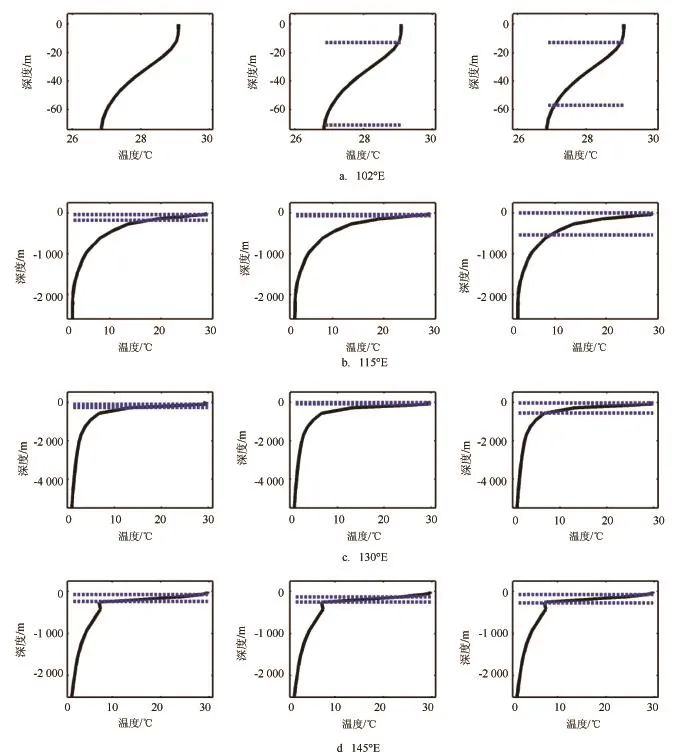
图3 10°N断面4个站位温度垂直剖面(黑色实线)与垂直梯度法(左边一列)、曲率极值点法(中间一列)、拟阶梯函数法(右边一列)所得跃层上下界面位置(蓝色虚线)
4 温跃层季节变化特征及讨论
我们利用曲率极值点法和拟阶梯函数相结合的方法,对于本文所使用的西北太平洋数值产品进行了温度跃层特征值的诊断分析。我们选取2月、5月、8月、11月15日数据代表冬、春、夏、秋4个季节的典型值。图5—8分别给出了冬季、春季、夏季、秋季温度跃层上界深度、下界深度、跃层厚度和强度分布特征,其中跃层厚度定义为跃层上界与下界深度之差,跃层强度定义为上、下界深度之间的平均温度梯度。
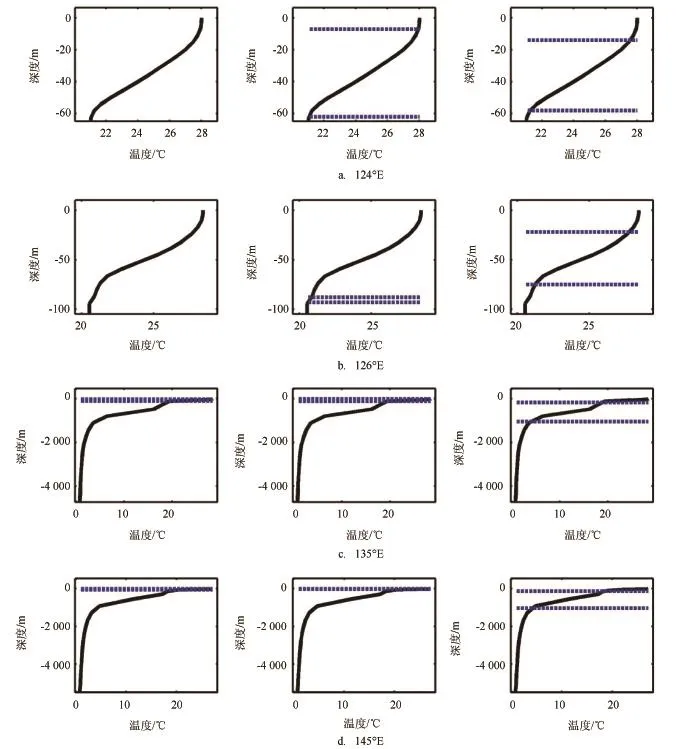
图4 30°N断面4个站位温度垂直剖面(黑色实线)与垂直梯度法(左边一列)、曲率极值点法(中间一列)、拟阶梯函数法(右边一列)所得跃层上下界面位置(蓝色虚线)
冬季,无论深海还是浅海,跃层强度均较弱,绝大多数海区弱于0.05℃/m,大于0.05℃/m的海区仅占约13%,实际上对于黄、渤海来讲,水深较浅,冬季水体基本混合均匀,利用本文使用的再分析数值产品诊断出的跃层强度也体现出这一特征。跃层上界深度在130°E以东的中纬度海域较深,可达80 m,其他海区大多在20 m以浅。深水区跃层厚度可达600 m以上。春季,随着太阳辐射的增强,浅水区跃层强度也在不断增大,特别是黄海、渤海、北部湾、泰国湾等区域。
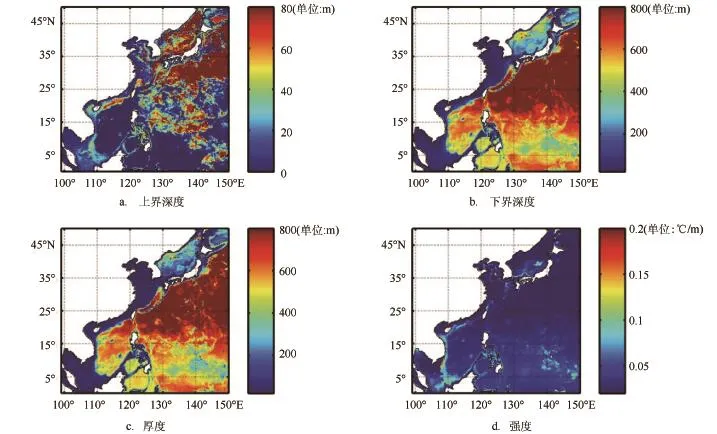
图5基于数值产品诊断出的冬季西北太平洋海域温度跃层分布图
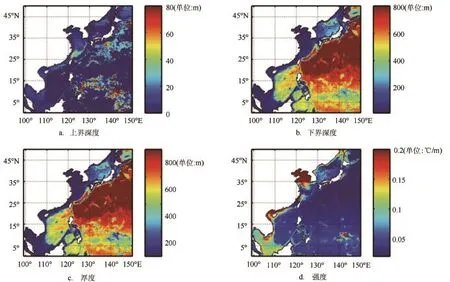
图6基于数值产品诊断出的春季西北太平洋海域温度跃层分布图
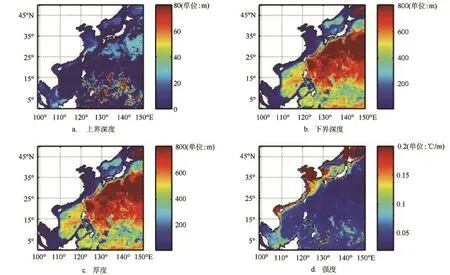
图7基于数值产品诊断出的夏季西北太平洋海域温度跃层分布图
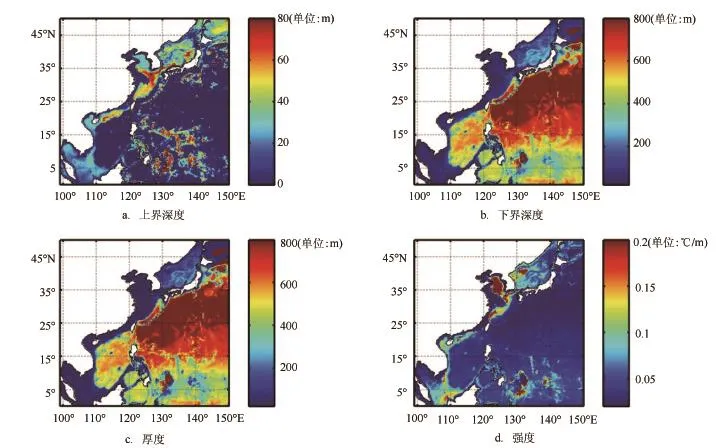
图8基于数值产品诊断出的秋季西北太平洋海域温度跃层分布图
夏季是跃层最强的季节,特别是浅海区,如黄海、渤海、北部湾等的大部分区域跃层强度大于0.2℃/m,统计结果表明跃层强度大于0.2℃/m的区域约占整个海区的7%,跃层强度大于0.05℃/m的区域约占整个海区的36%。跃层上界深度,浅水区一般在10—30 m之间,深水区大部分在10—60 m之间,少数区域上界深度超过80 m。相对于冬季和春季,夏季跃层厚度的空间分布模态变换不大。秋季,跃层强度逐渐变弱,浅海区域表现明显。以上温度跃层特征量的分布、演变特征均是基于本文使用的再分析数据得到的,更为准确可靠的跃层特征信息还需更多的观测资料支持。
总之,跃层是海洋中重要的物理现象,针对所研究的物理量不同,海洋中的跃层可分为温度跃层、密度跃层、盐跃层、声跃层等。目前常用的跃层分析方法有垂向梯度法、S-T法、拟阶梯函数法、最优分割法、曲率极值点法、三次样条数值函数分析法等。本文比较了垂向梯度法、曲率极值点法和拟阶梯函数法识别温跃层结果的异同。分析结果表明在跃层结构非常明显的情况下3种方法均能给出较为合理的结果,而且跃层上下界面位置相差不大。垂直梯度法由于有些剖面温度梯度没有超过阈值而探测不到跃层。采用曲率极值点法和拟阶梯函数相结合的方法,能够给出较为准确的跃层上下界面位置,即跃层上界选用曲率极值点法和拟阶梯函数法确定跃层上界的最大值,而跃层下界则选用拟阶梯函数的结果。利用使用的再分析资料,本文还初步诊断分析了西北太平洋冬季、春季、夏季、秋季温度跃层上界深度、下界深度、跃层厚度和强度分布演变特征。
参考文献:
[1]Turner J S,Kraus E B.A one-dimensional model of the seasonal thermocline,I,a laboratory experiment and its interpretation[J]. Tellus,1967,19(1):88-97.
[2]Gill A E,Turner J S.A comparison of seasonal thermocline models withobservation[J].DeepSeaResearchandOceanographic Abstracts,1976,23(5):391-401.
[3]Gregg M C.Diapycnal mixing in the thermocline:a review[J]. Journal of Geophysical Research,1987,92(C5):5249-5286.
[4]Gregg M C.Scaling turbulent dissipation in the thermocline[J]. Journal of Geophysical Research,1989,94(C7):9686-9698.
[5]Moum J N.Efficiency of mixing in the main thermocline[J]. Journal of Geophysical Research,1996,101(C5):12057-12069.
[6]Radko T,Marshall J.Eddy-induced diapycnal fluxes and their role in the maintenance of the thermocline[J].Journal of Physical Oceanography,2004,34(2):372-383.
[7]McDonagh E L,Bryden H L,King B A,et al.Decadal changes in the south Indian ocean thermocline[J].Journal of Climate,2005,18 (10):1575-1590.
[8]葛人峰,郭景松,于非,等.黄、东海陆架海域温度垂直结构类型划分与温跃层分析[J].海洋科学进展,2006,24(4):424-435.
[9]张婷婷,李培良,王雪竹,等.南海中部上层海洋温度的短周期振动[J].海洋湖沼通报,2009,(4):8-16.
[10]鲍献文,李娜,姚志刚,等.北黄海温盐分布季节变化特征分析[J].中国海洋大学学报,2009,39(4):553-562.
[11]吴巍,方欣华,吴德星.关于跃层深度确定方法的探讨[J].海洋湖沼通报,2001,(2):1-7.
[12]葛人峰,乔方利,于非,等.陆架海区温跃层特征量的一种计算方法-拟阶梯函数逼近法[J].海洋科学进展,2003,21(4):393-400.
[13]郝佳佳,陈永利,王凡.中国近海温跃层判定方法的研究[J].海洋科学,2008,32(12):17-24.
[14]张旭,张永刚,聂邦胜,等.垂直梯度法与最优分割法确定温跃层边界的比较分析[J].海洋通报,2008,27(6):20-26.
中图分类号:P731.24
文献标识码:A
文章编号:1003-0239(2016)03-0041-09
DOI:10.11737/j.issn.1003-0239.2016.03.006
收稿日期:2015-04-08
作者简介:江伟(1975—),男,高级工程师,硕士,从事军事水文气象及规划论证。E-mail:htpyang@sina.com用到拟阶梯函数逼近法中,发现不同类型的跃层结构均可按照一个或多个拟阶梯函数进行最小二乘拟合来获得温跃层的特征量。郝佳佳等13]根据东海以及南海东北部多组资料,比较了拟阶梯函数法和垂向梯度法在浅海区(水深<200 m)、陆架坡折区(水深在200 m左右)和深水开阔区(水深>200 m)与实际水文廓线的拟合情况,发现在大洋深水区可以用垂向梯度法,浅水区采用拟阶梯函数法进行跃层结构分析。张旭等[14]比较了垂直梯度法和最优分割法确定温跃层边界的优劣。
Comparisons of three thermocline detection methods
JIANG Wei,XING Bo,LOU Wei,LIAN Ren-ming
(Marine Hydrometeorological Center,Beijing 100161 China)
Abstract:By using the reanalysis numerical data,vertical gradient method,extreme curvature method and quasi-step function approximation method are used to calculate the thermocline structure.Comparison results show that combination of extreme curvature method and quasi-step function approximation method can offer reasonable thermocline structure,i.e.,the upper boundary of thermocline can be determined by the larger value between the upper boundaries estimated by extreme curvature method and that by quasi-step function approximation method while the lower boundary is the value estimated by the quasi-step function approximation method.
Key words:thermocline;vertical gradient method;extreme curvature method;quasi-step function approximation method

