结构刚度优化问题模型比较研究

彭细荣（湖南城市学院，湖南 益阳 413000）



结构刚度优化问题模型比较研究

彭细荣
（湖南城市学院，湖南 益阳 413000）

摘 要：针对结构刚度优化问题存在不同优化模型，本文以悬臂梁分布参数优化问题为例，对体积比约束下柔顺度极小优化模型及位移约束下重量极小优化模型进行了比较。对集中荷载及均布荷载两种作用情况下，采用拉格朗日乘子法求解得到了设计变量梁高的分布函数表达式，并给出了最优解时梁的挠曲线方程，通过优化模型解析解及挠曲线方程的比较，得到结论：在单个集中荷载作用时，两种模型间可建立等价关系，但在均布荷载情况下，难以建立两种模型间的等价。

关键词：刚度优化；柔顺度；位移约束；模型比较

结构优化设计必须满足结构在强度、刚度及稳定性等方面的要求［1］。对结构刚度的优化问题，目前存在两种优化模型，一种是位移约束下重量极 小 化 模 型 （ Minimum Weight with a Displacement Constraint，简称MWDC模型），另一种是体积约束下结构柔顺度极小化模型（ Minimum Compliance with a Volume Constraint，简称MCVC模型）［2］。在尺寸及形状优化问题中，通常建立MWDC模型，很少建立MCVC模型，但在拓扑优化问题中，MCVC模型却研究得比MWDC模型更多［2-3］。例如，变密度法［4］（SIMP法［5］为代表）、水平集方法［6］、相场法［7］等通常均建立MCVC模型，只有少数方法如ICM法［8］、进化结构优化方法［9］等建立MWDC模型。MCVC模型在拓扑优化中研究较多，主要是由于模型求解的简单方便［10］。

本文应用拉格朗日乘子法，研究MCVC模型及MWDC模型的解析最优解，从而保证两种模型的比较建立在严格的理论推导基础之上，所得结论更具说服力。同时，给出的优化问题解析解可作为类似优化问题数值求解方法研究的考题。

1　MCVC模型与MWDC模型

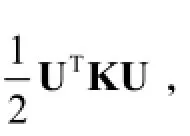
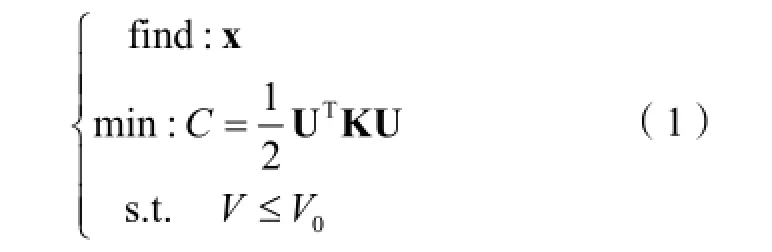
其中x为设计向量，V为结构总体积，V0为指定的体积上限约束。

大部分工程问题，包括各类国家规范，均是以位移限值的方式来提出对结构刚度的要求。位移约束下结构重量最小化的优化模型（MWDC模型）为：

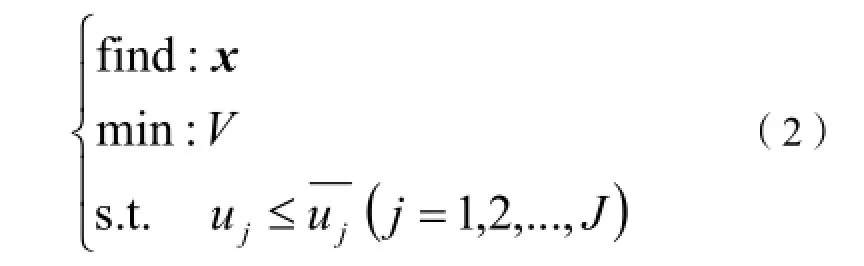
对悬臂梁分布参数优化问题，下面内容将针对上述两个优化模型，求解出最优解的解析解，并进行比较分析。

2　单个集中荷载作用悬臂梁分布参数优化及模型比较

如图1所示，悬臂梁受单个集中荷载F作用，梁截面宽度为 b，梁高 h（x）为设计变量。由于设计变量 h（x）为连续函数，所以此优化问题为分布参数优化问题。对 MCVC模型优化问题，设计h（x），指定体积约束V0，最小化结构总应变能C。

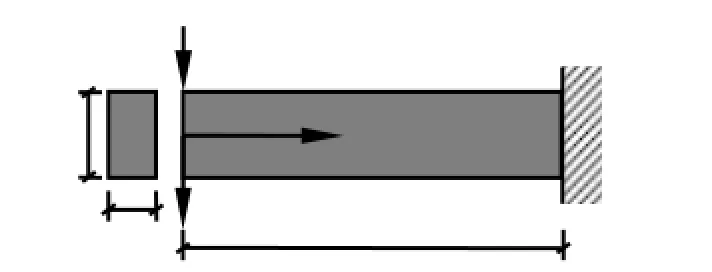
图1　悬臂梁受单个集中荷载作用的分布参数优化

梁截面惯性矩为：

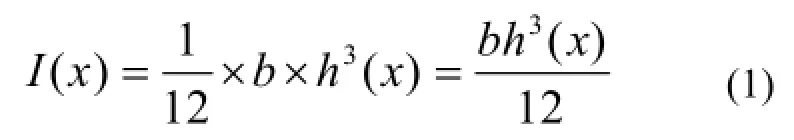
梁所受弯矩为：

由梁理论可得结构总应变能C为：

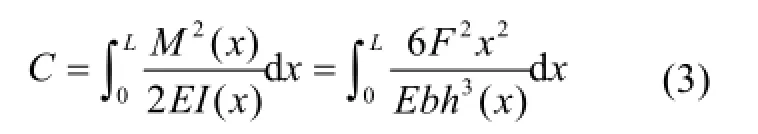
所以，建立的MCVC优化模型为：

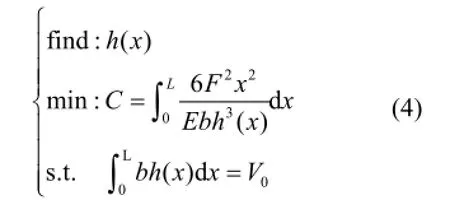
应用拉格朗日乘子法，式（4）优化模型对应的拉格朗日函数为：

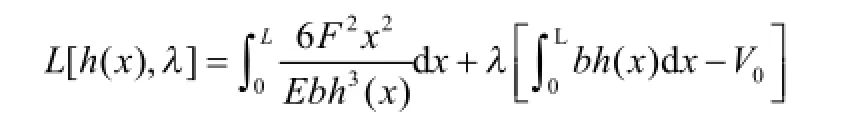
最优截面高度h（x）由下列条件确定：

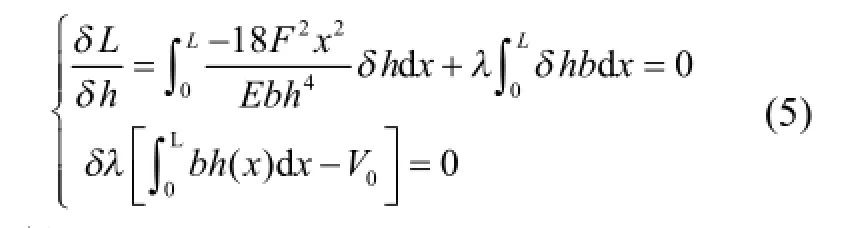
解得:

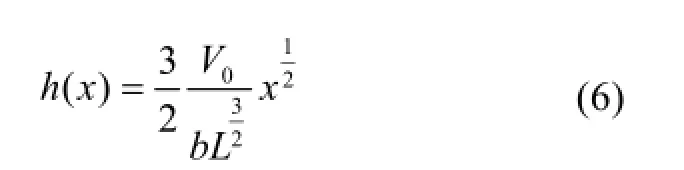
由梁理论，最优解时梁的挠曲线方程为：

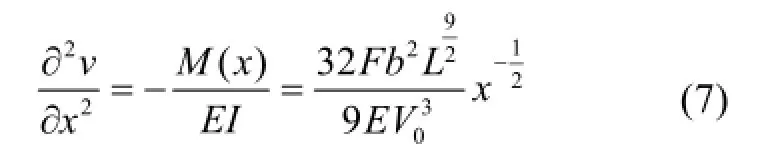
求解得到梁的挠曲线为：

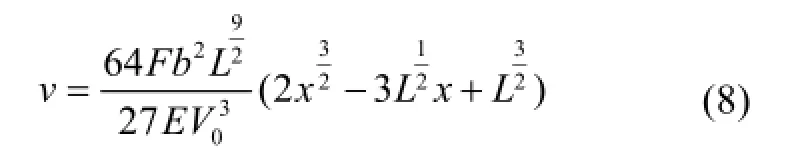
所以，梁自由端挠度为：

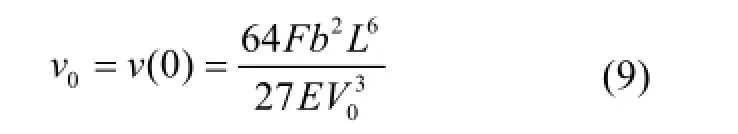
由梁理论，梁自由端挠度还可用单位力法计算：

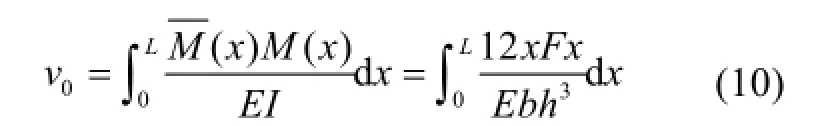
同样可以得到与式（9）相同的结果。

以此位移值作为约束条件，设计 h（x），最小化结构总体积（即最小化结构总重量），建立的MWDC模型为：

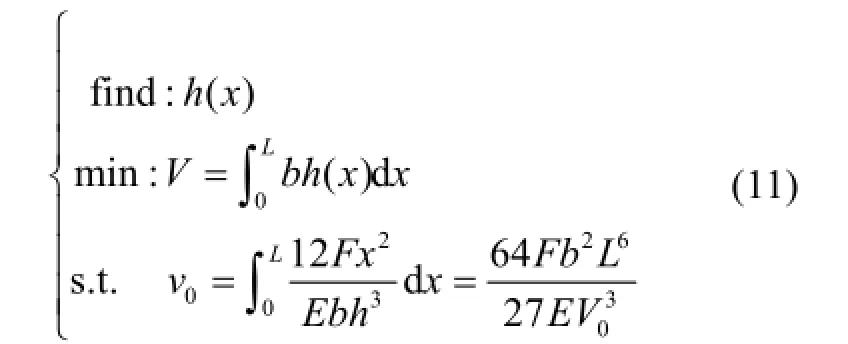
同样应用拉格朗日乘子法，式（11）优化模型对应的拉格朗日函数为：

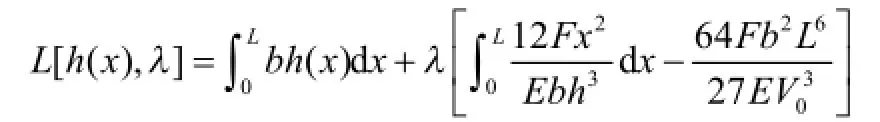
最优截面高度h（x）由下列条件确定：

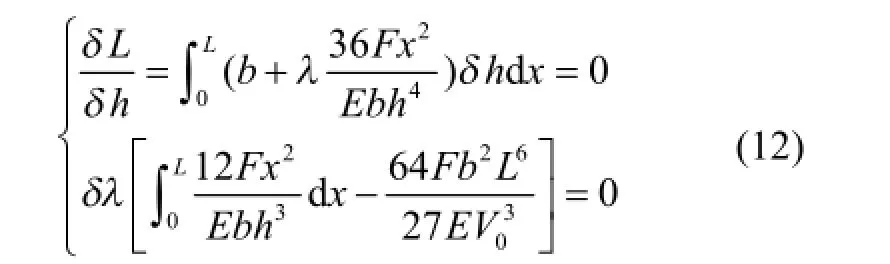
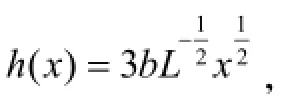
取V0=b×2b×L ，则最优化梁截面高度变化如图2所示。

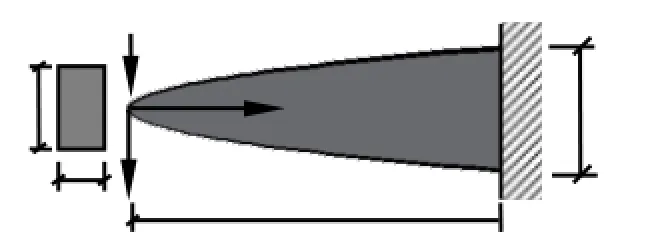
图2　优化求解得到梁截面高度变化

由此可见，当MWDC模型的位移约束取荷载作用方向上MCVC模型最优解的位移值时，MWDC模型得到的最优解体积正好是 MCVC模型所指定的体积约束值，两个模型得到的最优截面高度分布函数是相同的，最优解时梁的挠度曲线也是相同的，即两个模型是完全等价的。

3　均布荷载作用悬梁参数优化及模型

梁所受弯矩为：

由梁理论可得结构总应变能C为：

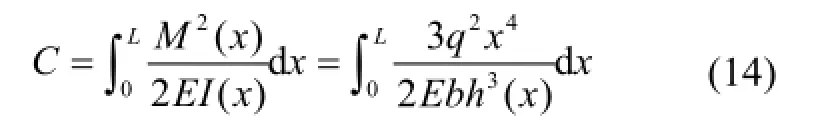
所以，建立的MCVC优化模型为：

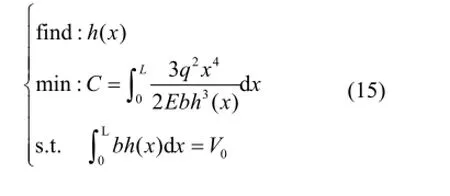
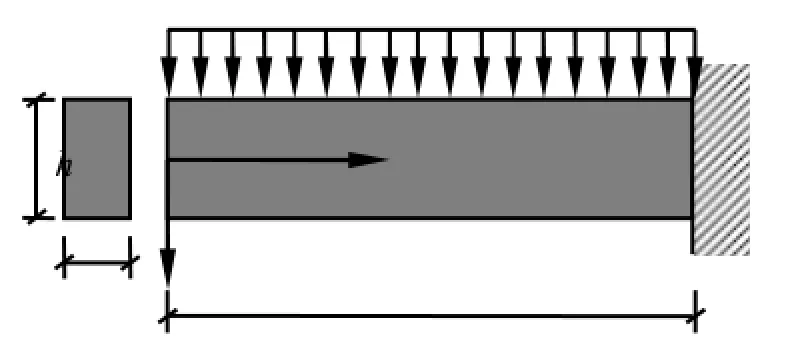
图3　悬臂梁受均布荷载作用的分布参数优化

应用拉格朗日乘子法，式（15）优化模型对应的拉格朗日函数为：

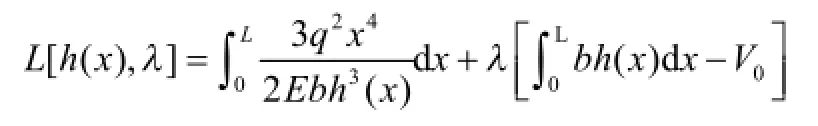
最优截面高度h（x）由下列条件确定：

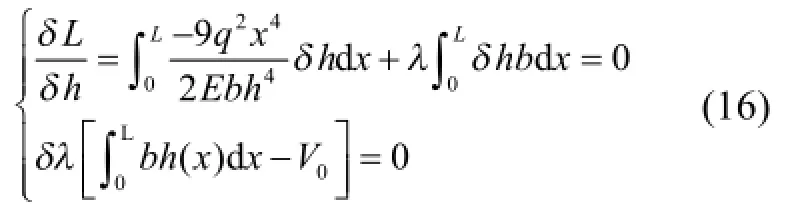
解得:

取V0=b×2b×L ，则h（x）=4bL-1x，最优化梁截面高度变化如图4所示。

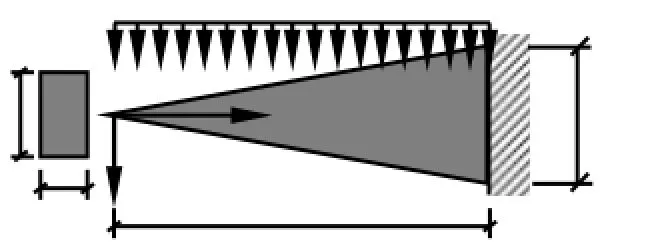
图4　悬臂梁受均布荷载作用MCVC模型求解得到梁截面高度变化

由梁理论，最优解时梁的挠曲线方程为：

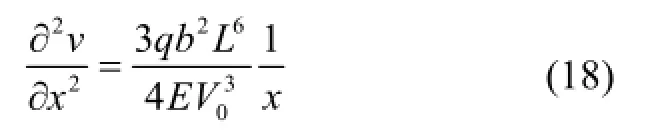
求解得到梁的挠曲线为：

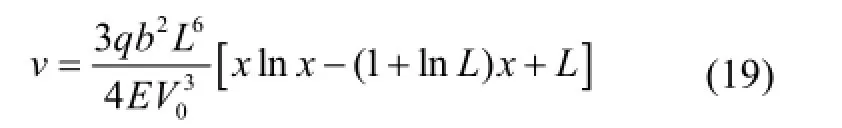
所以，梁自由端挠度为：

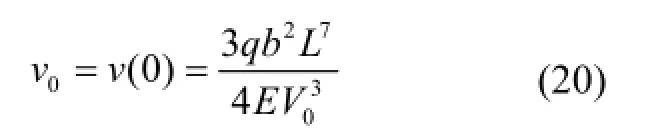
梁自由端挠度用单位力法计算：

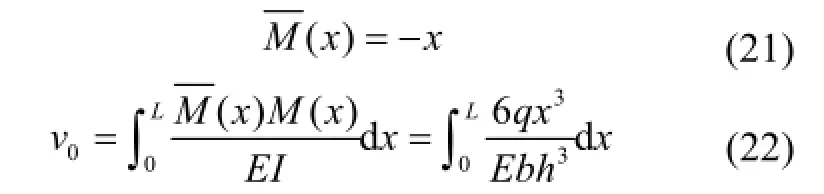
同样可以得到与式（20）相同的结果。

以MCVC模型最优解时自由端位移值（即式（20）所示）作为约束条件，设计 h（x），最小化结构总体积（即最小化结构总重量），建立MWDC模型为：

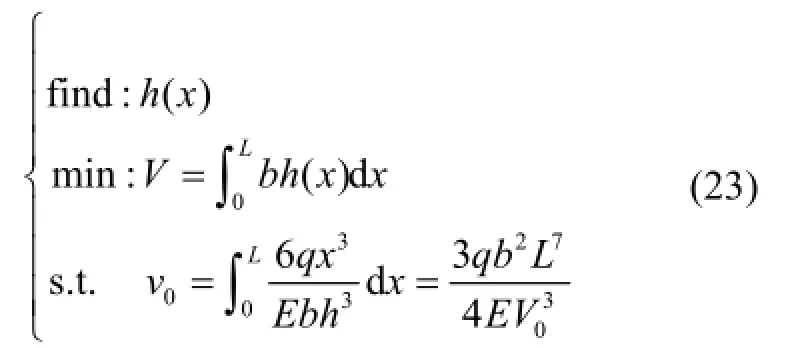
同样应用拉格朗日乘子法，式（11）优化模型对应的拉格朗日函数为：

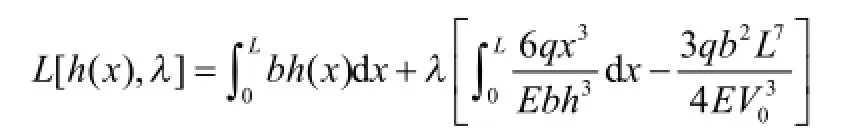
最优截面高度h（x）由下列条件确定：

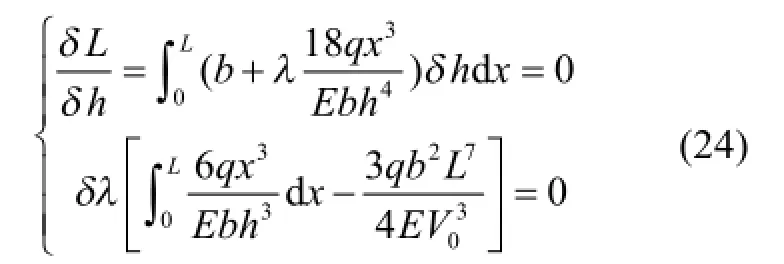
解得:

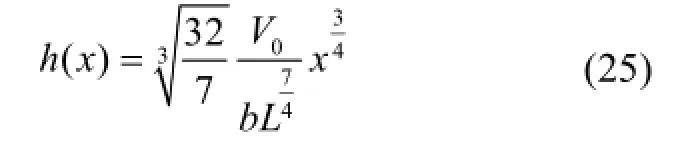
取V0=b×2b×L ，则h（x）=3.3bL-3/4x3/4，最优化梁截面高度变化如图5所示。

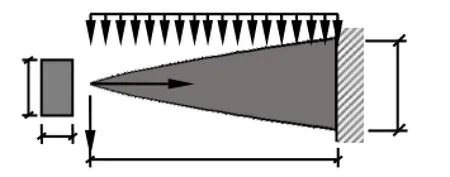
图5　悬臂梁受均布荷载作用MWDC模型求解得到梁截面高度变化

MCVC模型与MWDC模型得到的最优解时梁的高度变化比较如图6所示。

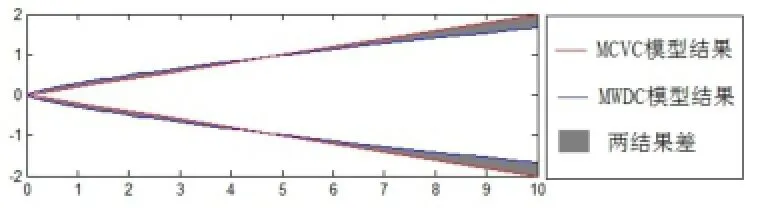
图6　最优解梁高变化比较

求解得到梁的挠曲线为：

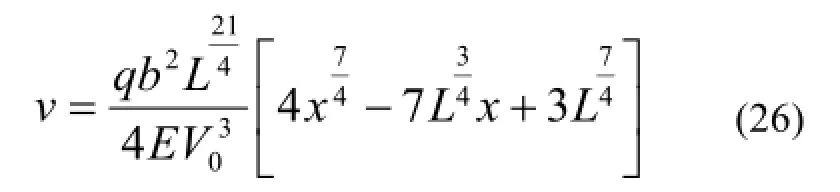
比较式（26）与式（19）可知，MWDC模型与MCVC模型最优解时梁的挠曲线不同，如图7所示。

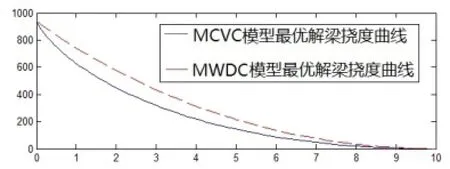
图7　均布荷载作用下两种模型最优解梁挠曲线

梁自由端挠度为：

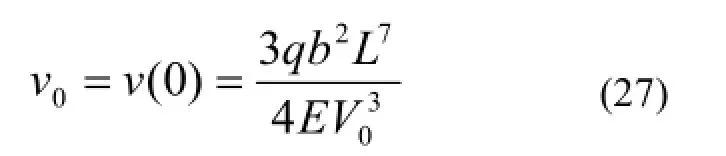
与式（20）相同，满足式（23）中位移约束条件。

此时梁的总体积为：

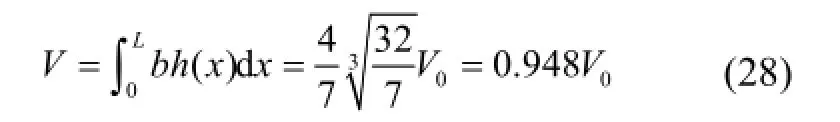
MWDC模型得到的最优解时梁的总体积比MCVC模型指定的体积约束值V0小。

4　结论

针对结构刚度优化问题，本文对悬臂梁受单个集中荷载作用及均布荷载作用两种情况，应用拉格朗日乘子法求得了MCVC模型及MWDC模型的最优解及对应的梁挠曲线的解析表达式。主要结论如下：

（1）在单个集中荷载作用下，当MWDC模型位移约束荷载作用点的位移时，MCVC模型与MWDC模型可以建立等价模型。即MWDC模型位移约束值取 MCVC模型最优解时对应的位移值，得到的最优解结构总体积正好等于MCVC模型中指定的体积约束。

（2）在均布荷载作用下，当MWDC模型仅约束一点位移值时，MCVC模型与MWDC模型所得结果完全不同。MCVC模型与MWDC模型间很难建立等价模型。

参考文献：

［1］隋允康.建模·变换·优化——结构综合方法新进展.大连：大连理工大学出版社，1996.

［2］隋允康， 叶红玲. 连续体结构拓扑优化的ICM方法［M］. 北京:科学出版社， 2013.

［3］易桂莲. 移植 ICM方法拓展的结构拓扑优化SIMP方法. 北京：北京工业大学. 博士学位论文， 2014.

［4］Mlejnek H P，Schirrmacher R.An engineer’s approach to optimal material distribution and shape finding［J］.Computer Methods in Applied Mechanics and Engineering，1993， 106（1/2）: 1-26.

［5］Rietz A.Sufficiency of a finite exponent in SIMP （power law）methods ［J］. Structural and Multidisciplinary Optimization，2001，21（2）: 159-163.

［6］Osher S J，Santosa F. Level set methods for optimization problems involving geometry and constraints: I. Frequencies of a two-density inhomogeneous drum ［J］. Journal of Computational Physics，2001，171（1）: 272-288.

［7］Bourdin B，Chambolle A. Design-dependent loads in topology optimization ［J］. ESAIM: Control，Optimisation and Calculus of Variations，2003，9（8）:19–48.

［8］Y. K. Sui，D. Q. Yang. A New Method for Structural Topological Optimization Based on the Concept of Independent Continuous Variables and Smooth Model ［J］. Acta Mechanica Sinica，1998，18（2）: 179-185.

［9］Y. M. Xie，G. P. Steven. A Simple Evolutionary Procedure for Structural Optimization ［J］. Computers & Structures，1993，49: 885-896.

［10］Bendsoe M P，Sigmund O. Topology optimization: theory，methods and applications［M］. 2nd ed. New York: Springer Berlin Heidelberg，2003.

［11］Peter W. Chritensen，Anders Klabring. An introduction to structural optimization. New York: Springer Berlin Heidelberg，2009.

（责任编辑：廖建勇）

中图分类号：TU391

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01.001

文章编号：1672–7304（2016）01–0001–04

作者简介：彭细荣（1972-），男，江西宜春人，博士后，副教授，研究方向：结构优化设计、结构监测。

A Comparative Study on Models of Structural Stiffness Optimization Problems

PENG Xi-rong
（Hunan City University，Yiyang Hunan 413000）

Abstract:Different optimization models exist for the structural stiffness optimization problems. Taking the distribution parameter optimization problem of a cantilever beam as an example，the optimization model with minimizing structural compliance objective subject to specified volume constraint and the optimization model with minimizing structural volume （or weight） objective subject to specified displacement constraints are compared. For a concentrated load and a uniformly distributed load cases，using the Lagrange multiplier method， the distribution function of beam section height is obtained，which is the design variable in optimization models. The extramural equation of optimal beams obtained by optimization is also derived an analytic expression. By comparing analytic solutions of the optimization model and the extramural equation of optimal beams，conclusions are obtained. For the case of a single concentrated load，equivalent relation can be built between the two kinds of model，but in the case of uniformly distributed load，it is difficult to establish the equivalence between the two models.

Keywords:Stiffness optimization；Compliance；Displacement constraints； Model comparison