城市公共交通系统中的最佳路径问题

刘香菊 杨夏青 乔 石 房 丽

（齐鲁理工学院 山东济南 250200）



城市公共交通系统中的最佳路径问题

刘香菊 杨夏青 乔 石 房 丽

（齐鲁理工学院 山东济南 250200）

摘 要：通过分析城市公共交通系统网络图的特点，采用改进的Dijkstra 算法的最短路径问题构造公共交通网络模型。最佳乘车路线的获得，需要在满足换乘次数要求的基础上，提出换乘的实现算法，并在此过程中采用用换乘矩阵的形式描述最短路径中的站点及线路。

关键词：公共交通系统 最佳路径 最短路 最小换乘

一、引言

研究公交换乘的问题，首先要解决的问题是合理地表述公共交通网络模型；其次还需要对公交换乘问题思想做准确描述［2］。本文将解决换乘算法的实现问题，在此过程中还需综合考虑换乘次数的因素，距离因素的影响。

二、城市公共交通系统的特点［3］

与道路网络有所不同，城市公共交通系统有其自身特点，公交网络不能直接采用与道路网络相同的模型。

1.结点性质

在模拟不同公交线可换乘情况［4］时，需要考虑空间上比较接近的不同线路但同名的公交站点的抽象问题。

2.弧段性质

由于弧段与属性之间的一对多的关系，那么就会导致需重复记录在公共交通系统中，每条公交线路通过的弧段，这必然导致数据冗余问题的出现。

3.有向线性质

由于边的有向性不能体现公交系统图有向性特点，因此需要考虑另外的解决方法，即通过引入有向线路集的方法来解决。

三、建立城市公交系统模型

距离最短路段及最少换乘公交线路的集合构成了最优出行路径。

本文将交通网络模型采用“结点―弧段（可有多条弧段）―有向线”的数据结构来存储网络图。公交网络如图1所示。

四、公交换乘问题的解决思想

为解决公交换乘问题，我们需要做下面一些具体工作：

1.求解最短路径及其上的各个站点。

2.为获得换乘方案，需先构造最短路径站点及线路对应的换乘矩阵，并求解。

五、最短路径求解

1.经典最短路径算法概述

（1）Dijkstra算法

（2）Bellman-Ford-Moore算法

（3）Floyd算法

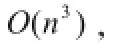
（4）启发式搜索算法——A*算法

A*算法提高了搜索过程的效率。引入已知的全局信息作为选择下一个被检查的结点的条件，为合理评价可能性的量度（该结点处于最优路线上的）需对当前结点距终点的距离作出估计。

2.公交线路查询不适合采用传统的Dijkstra算法

但是对公交网络来说，由于如下几方面原因，公交线路的查询采用Dijkstra算法是不适合的：

（1）数据结构复杂。

导致公交线路网络图的数据结构模型复杂的原因主要是公交网络节点与连通性的特殊性。

（2）算法时间长。

使用基于网络的权矩阵及Dijkstra 算法求解最短路径问题，在存储图形数据和进行运算时，需定义由网络的结点数构造的数组，当网络的结点数较大时大数组运算浪费时间。

3.基于改进 Dijkstra 算法的最短路径求解

由于存在上述的缺陷，采用基于点边拓扑关系的最短路径算法。主要步骤如下：

（1）将目标结点作为已到达结点，标志为已到达结点。

（2）若已到达结点和起始结点相同，则执行第（6）步，否则执行第（3）步。

（3）如果存在未搜索结点则继续第（4）步，否则执行第（6）步。

（4）扫描标志为已到达结点的结点的关联结点，这些关联结点不包括在已搜索节点表中已经存在的结点。

（5）重复执行第（2）步至第（4）步。

（6）为找出最短路径，需从起始结点到目标结点对所有的已到达结点对进行追踪。

六、实现公交换乘的数学描述

图 2：矩阵（1）

1.换乘矩阵存储方式的改进

若公交线路比较复杂，将导致矩阵（1）规模很大。公交线路矩阵表也可以作些改进。方法如下：

若最短路径上刚好包含了某条线路所经全部站点，则在该条线路的关联站点数组中将保存该这条路径上站点的序号（该站点在矩阵中的位置号）。

如矩阵（1）中线路关联站点数组，空间浪费会有效减少。

2.多次换乘的实现流程

实现矩阵（1）中任意两站点之间的换乘的问题的实现方法，可以采用用递归方法。具体流程图如图3。其中，起始站点在矩阵中的位置号用来表示；目标站点在矩阵中的位置号用来表示；中转次数为。求解与间的直达线路问题的方法，用来实现。

3.换乘方案的确定

表1 直达数据块列表

最简单的情形就是0次换乘，通过图3流程求解出来的直达数据块只有1个，如从起始点A至目标点B，不用换乘。如果直达数据块是不存在的，需要1次换乘的搜索。一次及以上的换乘的情况，得到的直达数据块可能很多。这样，在直达数据块列表中就存储了3个直达数据块，如表1所示。

从表1中可以看出，要确定A站点到B站点的换乘方案，次数更多的方法依此类推。

七、结论

本文研究乘车路线问题采用的主要理论是最短路径理论。首先获得构成最短路径的站点；最佳乘车线路的获得需要由这些站点及公交线路并采用换乘矩阵的方法。

参考文献

［1］牛学勤 ，王炜. 基于最短路搜索的多路径公交客流分配模型研究［J］. 东南大学学报. 2002，32（6），917-919；

［2］杨新苗， 王炜， 马文腾. 基于城市道路网的最短路径分析解决方案［J］. 小型微型计算机系统， 2003，24（7），1390-1393；

［3］陈立潮，刘玉树，张永梅，潘广贞. 城市交通智能咨询系统的设计与实现［J］. 计算机工程， 2003，29（1），32-34；

［4］夏春林 ，蒋瑞波 ，宋伟东. 道路网络中最短路径的算法与实现［J］. 辽宁工程技术大学学报， 2003，22（2）.180-181；

［5］张国强，晏克非. 城市道路网络交通特性仿真模型及最短路径算法［J］. 交通运输工程学报.2002，2（3），60-62；