基于主成分回归分析的需水预测研究
张少杰,游 洋
(1.南京市长江河道管理处,江苏 南京 210011;2.江苏省水利厅,江苏 南京 210029)
基于主成分回归分析的需水预测研究
张少杰1,游洋2
(1.南京市长江河道管理处,江苏南京210011;2.江苏省水利厅,江苏南京210029)
摘 要:水资源是城市发展的动力,需水量准确预测对城市可持续发展具有重要意义。需水量受多重因素影响,单一使用多重线性回归难以保证预测的准确性和科学性。根据南京市2005—2014年7个经济、社会发展相关指标,利用主成分回归分析建立模型使用原始变量对用水量进行预测。结果表明,应用主成分回归模型进行需水预测,比多重线性回归模型精度高,也较好地拟合了实际用水量。
关键词:水资源;需水预测;主成分;回归;南京
1 引言
水是维持经济社会发展不可或缺的基础性、战略性资源,日常生产、生活的方方面面都离不开水资源。需水预测是水资源合理配置、科学利用的重要内容之一,也是可持续发展、经济结构调整的重要部分[1]。需水预测方法中较为简便的有定额法、多元回归分析法等。但由于水资源需求量与人口数量、经济发展程度、居民用水水平等诸多因素有关,单一一种方法难以保证预测的准确性和科学性[2]。主成分分析和多元回归分析相结合的方法,可有效
2 研究方法
主成分回归分析是先通过主成分分析提取主要影响因素,用较少的综合指标,通过多元回归分析,较全面地反映影响因素,并将标化方程转换为一般方程,对水资源需求量进行预测。
2.1主成分回归
主成分分析法的本质是利用降维的思想,通过数学变换,用尽量少的变量最大化保留原有变量信息,其原理是:若有n个原始变量为xi,进行数据标准化、KMO及Bartlett检验确定是否适用主成分分析后,通过计算关系数矩阵的特征值、特征向量、方差贡献率、累计贡献率确定主成分及个数m(m<n)[3],则:
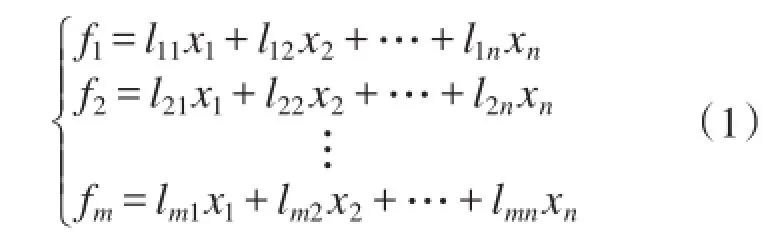
式中:fm分别为原始变量的第m个主成分;lmn为其对应系数。
按累计方差百分比选择主成分,并以标准化后的ZY为因变量、主成分 fi作为自变量进行回归分析,并按式(1)得出标化因变量ZY与标化自变量ZX的回归模型:
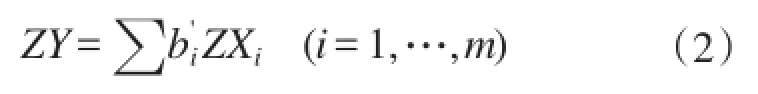
式中:b'i为标化回归方程的第i个标化偏回归系数。
将标化方程通过式(3)、(4)化为一般回归方程:
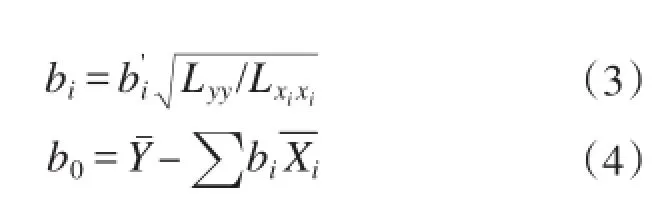
式中:b0为常数项;bi为一般回归方程的第i个偏回归系数;Lxixi为Xi的离均差平方和;Lyy为Y的离均差平方和。
2.2精度控制与检验
对拟合精度控制与检验主要有多重共线性诊断、拟合误差和偏回归系数的检验[4]。多重共线性诊断常用方差膨胀因子VIF,一般VIF>10表示存在多重共线性。拟合误差用确定系数R2度量,其表达式为:
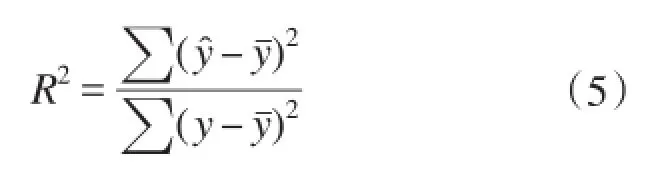
偏回归系数用统计量t检验,其表达式为:
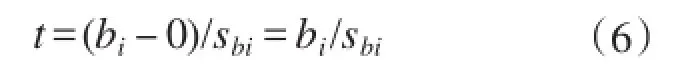
式中:sbi为bi的标准误差。t检验是对偏回归系数是否等于0进行的统计学检验。
3 实例分析
3.1研究区概况及水资源特点
笔者以南京市为例,采用主成分回归对需水量进行预测。南京市地处长江下游、江苏省西南部,属于北亚热带季风气候,辖区内有长江、水阳江、固城湖、石臼湖、滁河、秦淮河,多年平均气温15.4℃,多年平均年降水量1 082.3 mm,多年平均水资源量30.22亿m3,其中地表水资源量24.16亿m3,地表水资源主要来源于降水,6、7、8月降水产生地表水资源量占全年的50%以上。本地多年平均水资源量30.22亿m3,用水总量红线45亿m3,过境水量近9 000亿m3,主要来自长江、水阳江和滁河,其中长江过境水资源量占到99%以上。全市用水总量的96%以上来自长江。
3.2影响因子分析
遵循可靠性、科学性、代表性、全面性等原则,从2005—2014年《南京市统计年鉴》及2005—2014年《南京市水资源公报》选取2005—2014年人口X1、GDPX2、工业总产值X3、有效灌溉面积X4、万元GDP用水量X5、固定资产投资X6、农业产值X7、供水生产能力X88个评价指标,预测实际用水总量Y。评价指标中基本涵盖农业、工业、生活等多个方面用水因素。
3.3共线性诊断
对各项指标组成的矩阵进行多重共线性诊断,各因素的方差膨胀因子VIF见表1。因此,可得出X1,X2,X3,X4,X5,X6,X7均存在良好的共线性,而X8共线性较小,为确保结果的准确性,将其予以排除。

表1 各变量方差膨胀因子VIF
3.4KMO及Bartlett球形检验
对X1—X7的数据进行标准化,标准化后的数据见表2。KMO是检验偏相关系数的指标,取值在0~1,越接近1越适宜进行主成分分析。对标准化后的数据进行KMO检验和Bartlett球形检验,以确定是否适宜进行主成分分析。
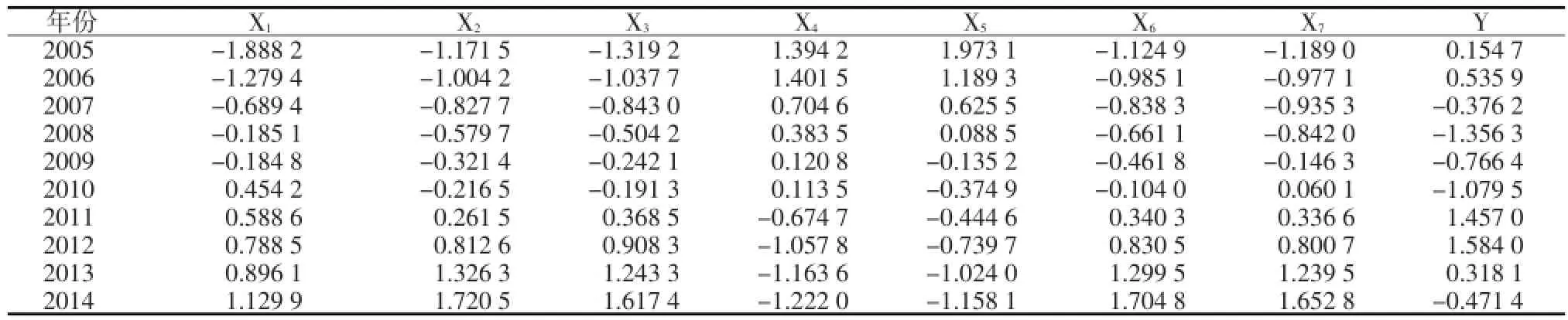
表2 南京市2005—2014年用水量及影响因子标准化矩阵
对上述标准化数据进行检验,得出其KMO值为0.775。此外,Bartlett球形检验得出的相伴概率为0.000,远小于显著性水平0.05,这说明变量之间相关性良好,适宜进行主成分分析。
3.5主成分因子确定
对标准化后的数据进行主成分分析,得出特征值、主成分贡献率和累计贡献率,见表3。主成分分析的结果显示:前4项主成分的方差累计贡献率已经大于99.9%,用这4个主成分可以最大限度包含原来7个影响因子。相应主成分载荷矩阵,见表4。
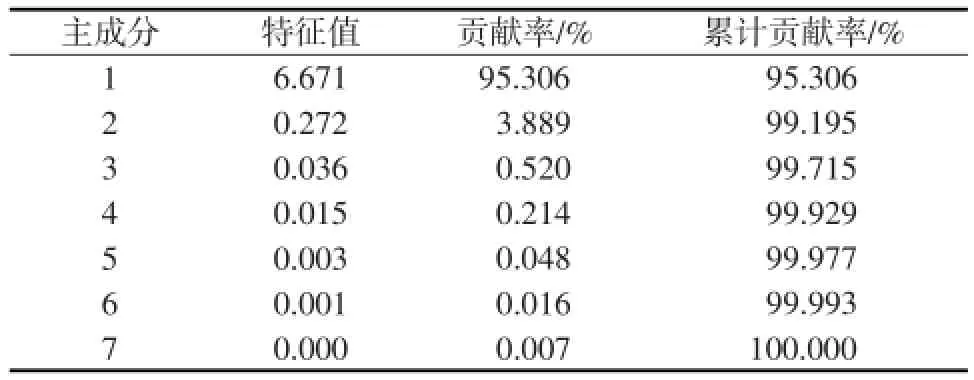
表3 特征值、主成分贡献率及累计贡献率
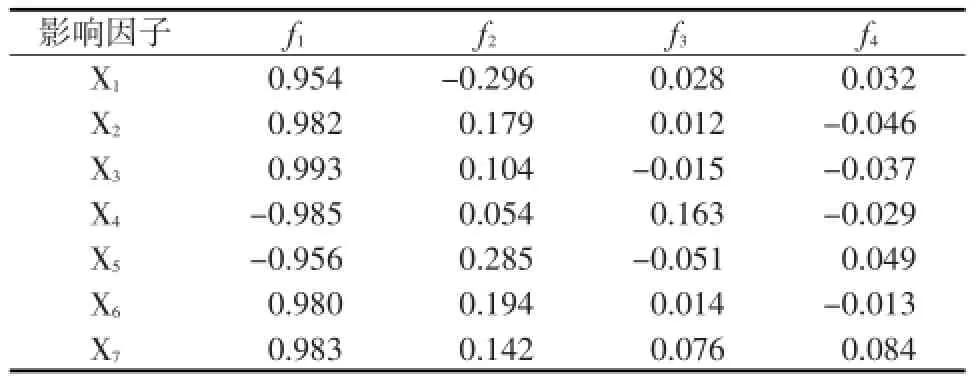
表4 主成分载荷矩阵
结合得出的4个主成分与各因子之间的关系式如下:

3.6主成分回归分析预测
按照上述4个公式,分别算出2005—2014的f1—f4的值,与标准化后的因变量ZY进行多重线性回归分析,再变换成原自变量与原因变量之间的关系,其主成分回归系数见表5。
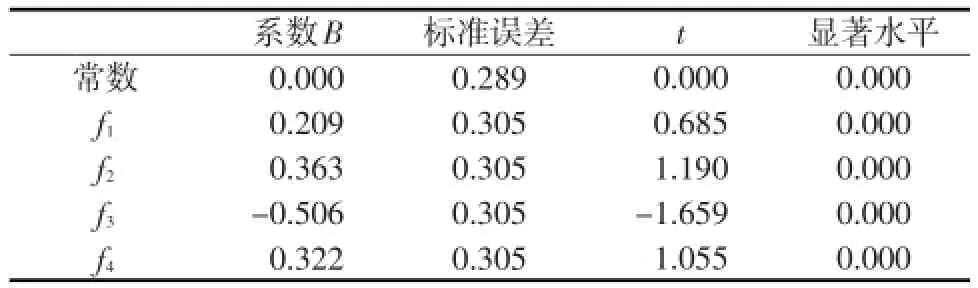
表5 主成分回归系数
根据式(3)、(4),将标准化后的主成分方程变换为原始变量回归模型(R2=0.978)为:

表6 多重线性回归系数
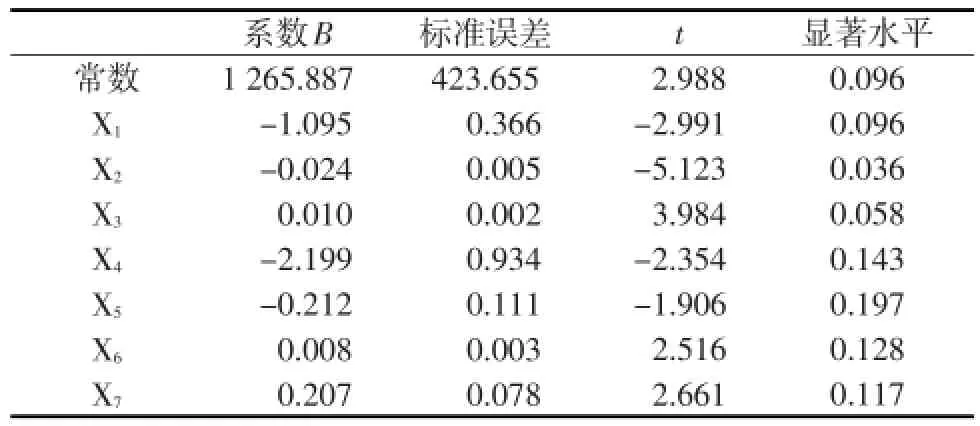
常数X1X2X3X4X5X6X7系数B 1 265.887 ---1.095 ---0.024 ---0.010 ---2.199 ---0.212 ---0.008 ---0.207标准误差423.655 --0.366 --0.005 --0.002 --0.934 --0.111 --0.003 --0.078 t -2.988 -2.991 -5.123 -3.984 -2.354 -1.906 -2.516 -2.661显著水平0.096 0.096 0.036 0.058 0.143 0.197 0.128 0.117
从表5—6可见,利用主成分回归建立的需水量预测方程各系数均通过了t检验,R2、显著水平均满足精度相关要求,并且在R2、t检验及显著水平方面均优于多重线性回归方程。为了更直观表示需水预测情况,现将2种方法预测结果与实际用水情况进行对比,如图1所示。从图1可以看到,主成分分析预测精度比多重线性回归精度高,也更接近实际用水量情况。
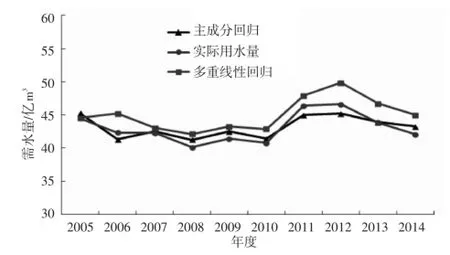
图1 模型预测结果与实际用水量对比
4 结语
需水量预测是进行水资源规划和管理的有效手段,与经济、社会等各项因素密切相关[5],运用最小二乘法进行多重线性回归,不能有效消除各因素之间的相关性,而采用多重共线性诊断和主成分分析,并将标准化方程转换为一般方程,使结果更加可靠和具有可操作性。笔者通过主成分回归确定需水总量的影响因素,与用水量进行回归分析,建立主成分与用水量的主成分回归方程。结果显示,R2、t、显著水平也均表明方程拟合的精度较高,通过与多重线性回归方程进行比较,主成分回归方程的预测值与实际值误差较小。因此,采用主成分回归预测城市需水量,可以为水资源科学管理、优化配置提供可靠依据。
参考文献
[1]刘卫林.几种需水量预测模型的比较研究[J].人民长江,2011,42(13):19-22.
[2]王春娟,冯利华,罗伟,等.主成分回归在需水预测中的应用[J].水资源与水工程学报,2014,24(1):50-53.
[3]李哲强,侯美英,白云鹏.基于SPSS的主成分分析在水环境质量评价中的应用[J].海河水利,2008(3):49-52.
[4]杨崇豪,张川云,吴文学.郑州市未来15年城市需水量预测研究[J].人民黄河,2006,28(11):30-32.
[5]王鹤鸣,李明良,王玉民.基于水资源可持续利用的区域需水预测分析[J].海河水利.2007(3):9-11.
中图分类号:TV214
文献标识码:A
文章编号:1004-7328(2016)03-0043-04
DOI:10.3969/j.issn.1004-7328.2016.03.015
收稿日期:2016—02—20
作者简介:张少杰(1983—),男,硕士,工程师,主要从事水资源节约、保护工作。解决这个问题,使预测的实用性、合理性都得到提高。
Research on the Water Demand Prediction based on Principal Component Regression
ZHANG Shao-jie1,YOU Yang2
(1.Yangtze River Waterway Management Department of Nanjing,Nanjing 210011,China;2.Jiangsu Provincial Water Resources Department,Nanjing 210029,China)
Abstract:Water resources are the driving force of urban development.Accurate predictiong of water demand is very impor⁃tant for urban sustainable development.Water demand is influenced by multiple factors,and the accuracy and the scientific using multiple linear regression is difficult to ensure the prediction.According to 7 factors of Nanjing 2005-2014,the mod⁃el was created to predict the water consumption by principal component regression analysis.The results show that the princi⁃pal component regression model is more accurate than the multiple linear regression model,and the principal component re⁃gression model is more fit the actual water consumption.
Key words:water resources;water demand prediction;principal component;regression analysis;Nanjing

