地震作用下防屈曲支撑减震结构附加有效阻尼比计算及变化规律研究

吴克川， 陶　忠， 韦光兰， 胡大柱， 余文正

(1.昆明理工大学 土木工程系，昆明　650500；2. 上海应用技术学院 城市建设与安全工程学院，上海　201418；3.上海蓝科建筑减震科技有限公司，上海　200433)



地震作用下防屈曲支撑减震结构附加有效阻尼比计算及变化规律研究

吴克川1， 陶忠1， 韦光兰1， 胡大柱2,3， 余文正1

(1.昆明理工大学 土木工程系，昆明650500；2. 上海应用技术学院 城市建设与安全工程学院，上海201418；3.上海蓝科建筑减震科技有限公司，上海200433)

摘要：基于《建筑消能减震技术规程》(JGJ 279-2013)的附加有效阻尼比计算方法，推导防屈曲支撑(Buckling-Restrained Brace， BRB)减震结构等效单自由度体系的附加有效阻尼比计算式，分析主体结构处于不同工作阶段附加有效阻尼比变化规律，并用自由振动衰减法验证其变化规律的正确性。结果表明，主体结构弹性时，附加有效阻尼比随结构变形增加先增大后减小；主体结构塑性时，BRB附加给结构的有效阻尼比与结构屈服后刚度有关。讨论阻尼器型BRB(记为第Ⅲ类)设计原则，并分析结构第一阶段抗震设计时附加有效阻尼比的取值原则。

关键词：防屈曲支撑；附加阻尼比；消能减震；自由振动衰减；双线性模型

消能减震技术[1]指在建筑结构特定部位布设消能装置，通过该装置吸收、耗散结构变形的振动能量，并通过改变结构动力特性减小其动力反应，已在美、日等国广泛应用[2-3]。我国将消能减震设计纳入《建筑抗震设计规范》(GB50011-2001)以来取得长足发展[4]。《建筑消能减震技术规程》(JGJ279- 2013)将消能减震结构设计标准及应用规范进行完善，会进一步促进该项技术的推广、应用。该规程规定，当消能减震结构主体结构处于弹性状态、消能器处于非线性状态时可用附加有效阻尼比的振型分解反应谱法计算，地震影响系数按消能减震结构总阻尼比确定，并给出基于ATC-33规范[5]的附加有效阻尼比估算式。因此合理确定消能器附加阻尼比对消能减震结构设计尤其重要。

消能装置据不同耗能原理可分为速度相关型、位移相关型。防屈曲支撑由于构造简单、耗能能力稳定，广泛用于新建及加固工程[6-7]。通过附加抗侧刚度及阻尼比降低结构地震反应，作用原理见图1。

图1　附加阻尼比减震原理Fig.1 Shock absorption with additional damping ratio

本文对各水准地震作用下防屈曲支撑附加给结构的有效阻尼比变化规律及设计取值进行研究、讨论，并采用自由振动衰减法[8]验证附加有效阻尼比变化规律的正确性以便用于消能减震结构设计。

1主体结构弹性时BRB附加给结构阻尼比

按JGJ279-2013规定，BRB采用双线性恢复力模型进行模拟，见图2。其中K为BRB弹性刚度；Keff为等效刚度；α为第二刚度系数；Fby为屈服承载力；Fbmax为极限承载力；uby为屈服位移；ubmax为极限位移。BRB附加给主体结构的有效阻尼比ζd为

(1)

式中：Wcj为第j个BRB在结构预期层间位移下往复循环一周所耗能量；Ws为BRB结构受水平地震作用的总应变能。

不计扭转影响的BRB结构受地震作用总应变能为

(2)

式中：Fi为质点i水平地震作用标准值；ui为质点i位移。

图2　BRB恢复力模型Fig.2 Hysteretic model of buckling restrained brace

将BRB减震结构运动等效为单自由度体系振动，BRB先于主体结构进入弹塑性阶段，记主体结构弹性位移为x，BRB耗散的地震能量与结构总应变能计算见图3。图中OA段为BRB屈服前与主体结构并联刚度；AB段为BRB屈服后与主体结构并联刚度；Kb为BRB弹性刚度；Kf为主体结构弹性刚度；Kef为BRB减震结构等效刚度；Db为BRB屈服位移。

图3　BRB耗能与结构应变能Fig.3 Buckling restrained brace hysteresis loop and structural strain energy

BRB耗散的地震能量为图3中滞回环面积，即

Wc=4Qd(x-Db)

(3)

式中：Qd为防屈曲支撑减震结构中BRB位移为0时荷载，即

Qd=Db(1-α)Kb

(4)

防屈曲支撑结构总应变能为图3中阴影部分面积，即

Ws=Kefx2/2

(5)

式中：Kef为防屈曲支撑减震结构等效刚度，即

(6)

将式(3)～式(6)代入式(1)，得

(7)

式中：k1为BRB弹性刚度与主体结构弹性刚度之比；μ为主体结构位移与BRB屈服位移之比，即

k1=Kb/Kf

(8)

μ=x/Db

(9)

(10)

图4　不同刚度比下结构有效阻尼比变化曲线Fig.4 Effective damping ratio curves under different stiffness ratio

式(7)中k1=1,3,5取值、α取值不同时结构附加有效阻尼比随结构变形曲线见图5，结构变形用μ=x/Db表征。由图5看出，结构附加有效阻尼比随α增大而减小；BRB弹性刚度与主体结构弹性刚度之比增大时结构附加有效阻尼比随α值变化更显著。

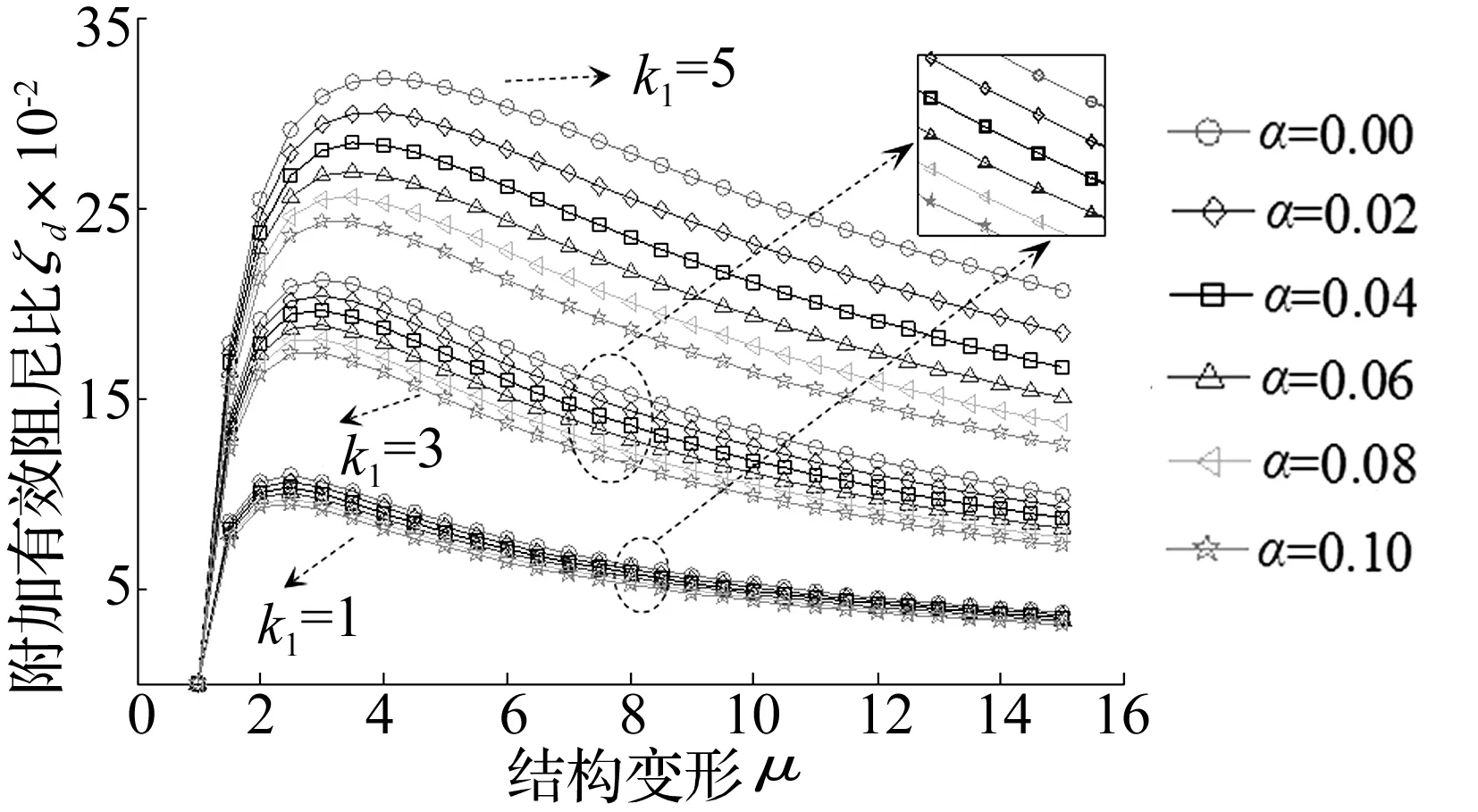
图5　不同第二刚度系数下结构有效阻尼比变化曲线Fig.5 Effective damping ratio curves under different post yield stiffness factor of BRB

2主体结构屈服后BRB附加结构阻尼比

消能减震主体结构屈服后可采用双线性模型模拟弹塑性行为[9]，则BRB耗散地震能及BRB减震结构总应变能计算见图6。其中β为主体结构屈服后刚度系数；Dy为结构屈服位移；OA、AB段同图3；BC段为BRB与主体结构均屈服后的并联刚度，其余参数含义同图3。为简化，记参数为

(11)

结构变形表征为

(12)

此时，结构等效刚度为OC段，即

Kby=αKb+Kf,Ky=αKb+βKf

(14)

将式(3)～式(5)、式(13)代入式(1)，得

(15)

将式(11)代入式(15)，得

(16)

将式(11)代入式(17)，有

(18)

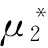
(19)

由式(19)看出，主体结构屈服后刚度小于一定数值时BRB附加给结构有效阻尼比取得极值。相反，BRB附加给结构有效阻尼比随结构变形增大而减小。

图6　弹塑性阶段BRB耗能与结构应变能Fig.6 Buckling restrained brace hysteresis loop and structural strain energy in structure plastic stage

确定BRB弹性刚度与主体结构弹性刚度比值k1及结构屈服位移与BRB屈服位移比值μ1后，BRB附加给结构的有效阻尼比在主体结构不同程度刚度退化时随结构变形变化曲线见图7。设μ1=4、k1=1，结构变形用μλ=μ2/μ1表征，取值范围[10]1～6，结构屈服后刚度退化程度用β表示。由图7看出，① 主体结构屈服后仍有较大刚度即β大于一定数值时，该有效阻尼比随结构变形增大而减小。此因结构进入塑性程度较小，弹性应变能变化仍起主要控制作用；② 主体结构屈服后刚度退化较多即β满足式(19)时，该有效阻尼比存在极大值；③ 主体结构刚度退化超过一定程度即β过小时，该有效阻尼比随结构变形增大而增加；④ 主体结构屈服后刚度趋于0即β≈0时，随结构变形增大该有效阻尼比趋于常数值2(1-α)k1/[π(1-α)k1+(π+παk1)μ1]；⑤ 结构变形一定时屈服后刚度退化程度越高该有效阻尼比越大。

图7　结构不同屈服刚度下附加有效阻尼比变化曲线Fig.7 Effective damping ratio curves under different post yield stiffness of structure

3BRB设计原则讨论及附加结构阻尼比变化规律分析

通常，BRB据不同性能目标及工程应用模式分为三类[11]：耗能型防屈曲支撑(第Ⅰ类)、承载型防屈曲支撑(第Ⅱ类)、防屈曲支撑型阻尼器(第Ⅲ类)。三类BRB在各水准地震作用的性能目标见表1。GB50011-2010[12](简称抗规)规定工程结构采用“两阶段，三水准”抗震设计方法，即多遇地震作用的附加有效阻尼比可用于确定反应谱的地震影响系数，直接关系结构抗震设计结果。对第Ⅰ、Ⅱ类BRB，因多遇地震作用下始终保持弹性，其附加给结构的有效阻尼比为0，此时地震影响系数直接按抗规要求确定，而对第Ⅲ类BRB，其在多遇地震作用下进入屈服耗能状态，须保证结构受设防地震、罕遇地震作用的抗震性能，防止出现危及生命的严重破坏。基于此，本文对第Ⅲ类BRB在各水准地震作用下附加给结构的有效阻尼比变化进行分析，讨论该阻尼比设计取值合适方法。

表1　BRB类型及性能目标

第Ⅲ类BRB不同屈服位移值μ1时结构附加有效阻尼比随结构变形变化曲线见图8。其中结构变形用μλ=μ2/μ1表征，阴影部分为结构受多遇地震作用的可能变形范围及附加有效阻尼比取值变化。由图8看出，① 阴影部分即BRB屈服位移较小时，结构附加有效阻尼比随结构变形增加先增大后减小，且取得极值。若按该有效阻尼比确定地震影响系数，则可能高估结构弹性阶段BRB的耗能能力，使结构在设防地震、罕遇地震作用下的抗震性能不足。② 阴影部分右边即BRB屈服位移较大时，结构附加有效阻尼比随结构变形增加亦先增大后减小，但极值在结构屈服点附近取得，即在设防地震作用的附加有效阻尼比值较多遇地震大。

图8　BRB不同屈服位移下附加有效阻尼比变化曲线Fig.8 Effective damping ratio curves under different yield displacement of BRB

为避免确定地震影响系数时附加有效阻尼比极值出现在(图8)阴影部分，BRB设计原则可为：对第Ⅰ、Ⅱ类，按JGJ279-2013对其性能指标及构造要求进行；对第Ⅲ类，在满足该规程性能构造要求基础上应遵循：① 确定合适的BRB屈服位移，使其在设防地震作用下附加给结构的有效阻尼比高于多遇地震；② BRB弹性刚度与主体结构弹性刚度较大时，应使设计的BRB第二刚度系数α尽量小。

按以上原则设计第Ⅲ类BRB，并令式(10)中μ*=μ1，有

(20)

则BRB屈服位移可按式(20)确定，即μ1满足该式时，可保证BRB附加给结构的有效阻尼比极值在结构屈服点附近取得。

由于BRB附加给结构的有效阻尼比随结构变形变化显著，因此确定地震影响系数时应分别按多遇、设防地震作用的附加有效阻尼比较小值确定[13]。

4工程实例验证分析

4.1自由振动衰减法

据有阻尼体系自由振动衰减理论[14],单自由度体系阻尼比计算式为

(21)

式中：δm=ln(sn/sn+m)为对数衰减率；sn，sn+m为单自由度体系第n、第n+m周振幅，m为两振幅间相隔周期数；ω，ωD为无、有阻尼体系自振频率。

将BRB减震结构顶点振动视为单自由度体系振动，据结构变形并结合式(21)验证分析BRB附加给结构有效阻尼比变化规律。具体实现过程为：① 将主体结构设为弹性，并指定其各阶振型阻尼比为0；② 对BRB减震结构施加瞬时激励，并考虑BRB非线性行为，计算BRB减震结构顶点振幅自由振动衰减时程曲线，见图9(a)；③ 据式(21)计算BRB附加给结构有效阻尼比随结构变形(用结构顶点振幅S与BRB屈服位移Db比值μS表征)变化曲线，见图9(b)；④ 计算结构多遇、设防地震作用的顶点振幅，并据图9(b)确定各地震作用的结构阻尼比，取二者中较小值作为BRB附加给结构的有效阻尼比进行结构抗震设计。

(a) 自由振动衰减时程　(b) 附加有效阻尼比变化图9　自由振动衰减法计算示意Fig.9 Free vibration decrement method

4.2工程概况

某框架结构办公楼见图10。该楼共15层，首层高4.5 m，标准层高3 m，总高46.5 m，抗震设防烈度8度(0.2 g)，设计地震分组为第二组，场地类别为Ⅱ类，场地特征周期Tg=0.4 s。

图10　办公楼框架结构Fig.10 RC frame structure

4.3附加有效阻尼比变化规律验证

按自由振动衰减法，采用ETABS有限元软件对BRB减震结构进行附加有效阻尼比分析。以X向自由振动为例，k1取不同值时结构顶点自由振动位移衰减时程曲线见图11。由图11看出，BRB减震结构顶点自由振动衰减符合有阻尼体系衰减规律；随k1增大历经相同自由振动时间后，顶点位移衰减程度越高；顶点位移衰减到一定程度即结构变形不足以使BRB产生塑性变形时顶点位移不再衰减，并以该变形保持稳定的自由振动。

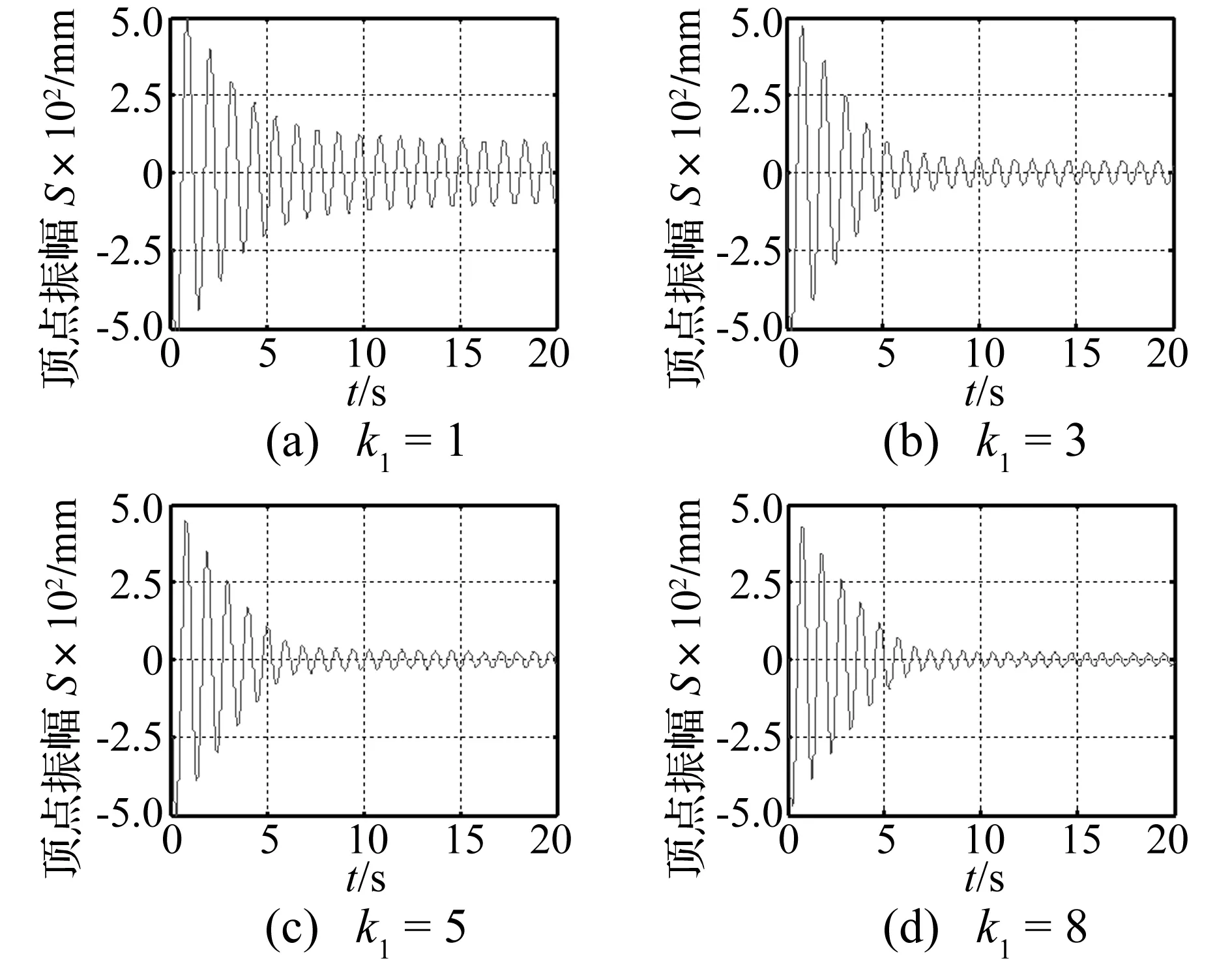
图11　BRB减震结构顶点自由振动衰减时程曲线Fig.11 Free vibration decrement of buckling restrained brace structure

不同k1取值的BRB附加给结构有效阻尼比随结构变形(用结构顶点振幅S与BRB屈服位移Db比值μS表征)变化曲线见图12。由图12看出，数值模拟所得附加有效阻尼比变化规律与理论推导一致，即附加有效阻尼比随结构变形先增加后减小；k1值越大附加有效阻尼比越高。

图12　不同刚度比下附加有效阻尼比变化曲线Fig.12 Effective damping ratio curves under different stiffness ratio

取k1=1、5，BRB第二刚度系数α变化时，附加有效阻尼比随结构变形(用结构顶点振幅S与BRB屈服位移Db比值μS表征)变化曲线见图13。由图13知，随k1值增大α变化对附加有效阻尼比影响更显著；α越小附加有效阻尼比值越大。

图13　不同第二刚度系数下附加有效阻尼比变化曲线Fig.13 Effective damping ratio curves under different post yield stiffness factor of BRB

分别考虑两种情形分析第Ⅲ类BRB设计原则及附加给结构有效阻尼比取值方法。情形1：仅按《建筑消能减震技术规程》(JGJ279-2013)要求设计BRB，不考虑屈服位移与主体结构屈服位移关系时可能出现的情况，即取μ1=20进行设计；情形2：按本文建议原则即式(20)进行设计。采用自由振动衰减法计算各水准地震作用下结构附加有效阻尼比，见表2。

表2　各水准地震作用下结构附加有效阻尼比

分别将两种情形多遇地震、设防地震作用下计算所得附加有效阻尼比代入等效分析模型进行时程分析，并与考虑BRB非线性行为时程分析结果比较。各楼层剪力对比见图14，对比结果为

(22)

式中：κi为等效分析模型与考虑BRB非线性行为模型各楼层剪力比；V0i为等效分析模型各楼层剪力；V1i为考虑BRB非线性行为分析模型各楼层剪力。

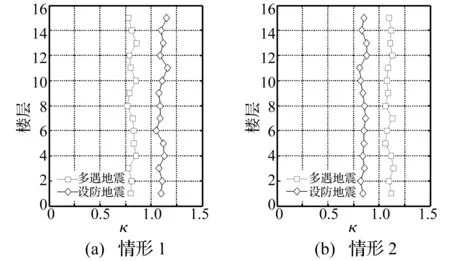
图14　不同水准地震作用下楼层剪力对比Fig.14 Story shear comparison under different seismic levels

由表2及图14看出，情形1计算所得多遇地震作用的附加有效阻尼比较设防地震大，若按此时多遇地震作用下的附加有效阻尼比进行结构第一阶段设计，则会高估BRB耗能能力，使结构偏于不安全；多遇地震作用下等效分析模型各楼层剪力小于考虑BRB非线性行为分析模型各楼层剪力(图14(a))即κ<1，亦说明按(情形1)多遇地震作用的附加有效阻尼比进行结构承载力设计，将高估BRB耗能作用；情形2计算所得多遇地震作用的附加有效阻尼比较设防地震小，由多遇地震作用(图14(b))κ>1知，若将此时多遇地震作用的附加有效阻尼比用于结构设计，则会提高结构抗震安全储备；在设防地震作用下，因情形1的κ>1，情形2的κ<1，即按情形2设计的BRB使结构在弹塑性阶段抗震储备能力更高。

5结论

通过研究主体结构处于不同工作状态时BRB附加给结构的有效阻尼比变化规律及取值方法，用自由振动衰减法验证规律的正确性，并结合JGJ279 -2013讨论BRB设计要求及设计原则，结论如下：

(1) 主体结构处于弹性阶段时，BRB附加给结构的有效阻尼比随结构变形增加先增大后减小；

(2) 该有效阻尼比随弹性刚度与主体结构弹性刚度比值增大而增加，随BRB第二刚度系数变化更显著，该系数越小附加有效阻尼比越大；

(3) 主体结构处于塑性阶段时该有效阻尼比随结构屈服后刚度系数减小而增加，该系数趋于0时，其值随结构变形增加趋于恒定常数。

(4) 确定合适的BRB屈服位移，可使其在设防地震作用下的有效阻尼比高于多遇地震；BRB弹性刚度与主体结构弹性刚度较大时，应尽量使第二刚度系数小，避免结构第一阶段设计时高估BRB耗能能力。

(5) 采用多遇、设防地震作用的附加有效阻尼比较小值进行设计，可提高结构在弹塑性阶段的抗震储备能力。

参 考 文 献

[1] 周锡元,闫维明,杨润林. 建筑结构的隔震、减振和振动控制[J]. 建筑结构学报, 2002, 23(2): 2-12.

ZHOU Xi-yuan, YAN Wei-ming, YANG Run-lin. Seismic base isolation,energy dissipation and vibration control of building structures[J]. Journal of Building Structures,2002, 23(2): 2-12.

[2] Constantinou M C, Symans M D. Experimental study of seismic response of buildings with supplemental fluid dampers[J]. Structural Design of Tall Buildings, 1993,2(2): 93-132.

[3] 李爱群. 工程结构减振控制[M]. 北京: 机械工业出版社, 2007: 114-150.

[4] JGJ 297-2013, 建筑消能减震技术规程[S].

[5] ATC33,NEHRP commentary on the guidelines for the seismic rehabilitation of buildings(FEMA273)[S]. Washington：FEMA,1997．

[6] Brow A P,Aiken D I,Jafarzadeh F J. Bucking restrained braces provide the key to the seismic retrofit of the wallace F.bennett federal building[J]. Modern Steel Construction, 2001, 27(3):36-42.

[7] 高杰，徐自国，任重翠，等.北京市轨道交通指挥中心(二期)屈曲约束支撑设计及动力弹塑性分析[J]. 建筑结构学报,2014,35(1):56-62.

GAO Jie,XU Zi-guo,REN Chong-cui,et al.Beijing rail transmit command center (phaseⅡ) energy dissipation technology and dynamic elasto-plastic analysis[J].Journal of Building Structure,2014,35(1):56-62．

[8] 巫振弘,薛彦涛,王翠坤,等. 多遇地震作用下消能减震结构附加阻尼比计算方法[J]. 建筑结构学报,2013,34(12):19-25.

WU Zhen-hong, XUE Yan-tao, WANG Cui-kun, et al.Research on additional damping ratio calculation methods under frequent earthquake[J].Journal of Building Structure,2013, 34(12): 19-25.

[9] 周云.防屈曲耗能支撑结构设计与应用[M]. 北京: 中国建筑工业出版社,2007: 86-89．

[10] FEMA 356, Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington, D.C: Federal Emergency Management Agency, 2000.

[11] 上海蓝科建筑减震科技有限公司. TJ屈曲约束支撑设计手册(第四版)[M]. 上海: 上海蓝科建筑减震科技有限公司,2011: 10-15.

[12] GB50011-2010,建筑抗震设计规范[S].

[13] 王维凝,阎维明,彭凌云. 不同水准地震作用下铅消能器附加给结构的有效阻尼比及其设计取值研究[J]. 工程力学,2014, 31(3):173-180.

WANG Wei-ning, YAN Wei-ming, PENG Ling-yun. Study on the additional damping ratio provide by lead dampers and its design values under different seismic levels[J].Engineering Mechanics,2014, 31(3):173-180.

[14] 尹帮辉,王敏庆,吴晓东. 结构振动阻尼测试的衰减法研究[J]. 振动与冲击,2014, 33(4): 100-106.

YIN Bang-hui, WANG Min-qing, WU Xiao-dong. Decay method for measuring structural vibration damping[J]. Journal of Vibration and Shock, 2014, 33(4): 100-106.

基金项目：国家科技支撑计划项目(2013BAK13B01)；国家自然科学基金青年科学基金项目(51408361)

收稿日期：2015-04-17修改稿收到日期：2015-07-07

通信作者陶忠 男，博士，教授，博士生导师，1968年生

中图分类号:TU352.1；TU311.41

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.024

Calculation of the additional damping ratio of buckling-restrained brace structure and its variation under earthquake

WU Ke-chuan1, TAO Zhong1, WEI Guang-lan1, HU Da-zhu2,3, YU Wen-zheng1

(1. Civil Engineering Institute, Kunming University of Science and Technology, Kunming 650500, China; 2. College of Urban Construction and Safety Engineering, Shanghai Institute of Technology, Shanghai 201418, China;3. Shanghai Lanke Building Damping Technology Co., Ltd., Shanghai 200433, China)

Abstract:Based on the calculation method in “Technical specification for seismic energy dissipation of building” (JGJ 279-2013), an additional effective damping ratio formula for single-degree-of-freedom system with buckling restrained braces was derived and the calculated damping ratios were analyzed under different conditions. The results were verified by the comparison with the results by the free vibration decrement method. The results show that:before the structure yields, the additional effective damping ratio increases at first and then decreases with the increment of structural deformation, and after the structure yields,the additional effective damping ratio varies with the stiffness of structure. The design principle for the buckling restrained brace and the selection method of the additional effective damping ratio were also discussed.

Key words:buckling restrained brace; additional damping ratio; energy dissipation; free vibration decrement; bilinear model

第一作者 吴克川 男，博士生，1988年生