基于弗德卡曼阶比跟踪的转子起停车故障特征提取方法及应用
温广瑞, 江 铖, 李 杨, 廖与禾
(西安交通大学 机械制造系统国家重点实验室, 西安 710049)
基于弗德卡曼阶比跟踪的转子起停车故障特征提取方法及应用
温广瑞, 江铖, 李杨, 廖与禾
(西安交通大学 机械制造系统国家重点实验室, 西安710049)
摘要:针对传统起停车过程分析采用短时傅里叶变换提取瞬时幅值及相位会损失瞬变信息的不足,用弗德卡曼阶比跟踪原理(Vold-Kalman Filter Based Order Tracking,VKF-OT)结合全息谱原理,提出新的转子起停车故障特征提取方法。由转子起停车瞬态响应数据中提取随转速变化的阶比分量,通过各阶分量复包络直接求幅值、相位,能克服傅里叶变换的平均效应,保留转子振动瞬变信息;通过VKF-OT集成转子截面振动信息,结合全息谱理论绘制阶比全息瀑布图,提取转子起停车状态的故障特征,并用于起停车瞬态动平衡。结果表明,该方法可有效提取转子典型故障特征、降低转子系统一阶临界振动。
关键词:转子;起停车;Vold-Kalman阶比跟踪;全息瀑布图;故障特征提取;瞬态动平衡
转子作为大型旋转机械中关键设备主体,成为故障高发部位。识别、诊断转子故障有重要意义[1-2]。目前转子故障识别诊断主要基于稳态振动特征, 尚无充分利用升、降速过程振动信息。起停车过程振动信号相当于宽频激励的动态响应,较稳态转速的振动信息含信息更丰富,但起停车过程中由于转速不断变化,信号为非平稳。传统的起停车分析将非平稳过程视为短时窗内的平稳信号,利用短时傅里叶变换及内插技术求出各时窗内信号幅值、频率及相位,会造成FFT平均效应,即对一段频率或幅值非恒定信号用FFT求频率幅值相位时会产生频率模糊、幅值相位失真现象。因此,对起停车信号分析须用能处理非平稳信号方法。
阶比跟踪方法[3-4]能提取与转速相关分量,由于转子故障在振动信号上表现为转频、倍频及分倍频分量,启停机过程中也希望能提取该分量,因此将阶比分析技术用于起停车分析较恰当[5]。传统的阶比跟踪多采用计算阶比方法[6],目的将时域非平稳信号转换成角域平稳信号。实质上转换成角域后幅值仍变化,无法完全避免FFT平均效应导致的幅值、相位误差,影响故障的识别、诊断。
Vold-Kalman阶比跟踪方法[7-8]不仅能分离近似阶比、交叉阶比,且能将提取的阶比分量以复包络及载波乘积形式表示,便于直接通过复包络求幅值、相位,彻底摆脱FFT的平均效应。
全息谱即将多个传感器振动信息在频域融合方法,能综合反映机组振动幅值、频率、相位信息,实际生产中能更准确识别转子故障[9-10]。本文将Vold-Kalman阶比跟踪技术与全息谱原理结合,将非稳态信号进行Vold-Kalman阶比分析提取主要阶比分量,据分量复包络求相应转速下振幅、相位,再结合全息谱分析方法对转子启停机信号进行特征参数提取,进而对转子进行故障识别与诊断。
1Vold-Kalman阶比跟踪方法
1.1Vold-Kalman阶比跟踪理论[11]
Vold-Kalman阶比跟踪滤波技术已由第一代发展到第二代,两代阶比跟踪滤波器均由状态方程、观测方程表示,但表示方法有区别。第二代Vold- Kalman阶比跟踪理论更成熟,将阶比信号表示成复包络及载波形式,通过解调方式提取阶比分量。
1.1.1第二代阶比跟踪基本原理
阶比信号可表示为复包络与载波的乘积,即
(1)
式中:k为基准频率或参考轴转速倍数,即被跟踪阶比;a(t)为复包络;Θk(t)为载波,即
(2)
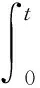
式(2)的离散形式为
(3)
1.1.2状态方程
由式(1)知,复包络ak(t)为载波Θk(t)的低频幅值调制,包络在局部范围内近似低阶多项式。用该多项式表示阶比信号幅值变化,系统状态方程为
sxk(n)=ε(n)
(4)
多项式阶比决定滤波器滤波效果,一、二、三阶多项式分别为
x(n)=x(n)-x(n+1)=ε(n)
(5)
(6)
3x(n)=x(n)-3x(n+1)+
3x(n+2)-x(n+3)=ε(n)
(7)
以上3式矩阵形式相同Ax=ε,即状态方程。
1.1.3观测方程
设定Vold-Kalman滤波器只提取单个阶比成分,则观测方程为
y(n)=x(n)Θ(n)+ξ(n)
(8)
据观测方程(8)得矩阵形式为
y-Cx=ξ
(9)
1.2基于第二代跟踪原理的阶比分量求解方法[12]
系统状态方程及测试方程对x(n)为欠系统,求方程解x(n)的前提为非阶比分量、背景噪声ξ(n)及非一致项ε(n)的平方和最小。状态方程非一致项ε(n)的平方和为
εTε=xTATAx
(10)
观测方程非阶比分量与背景噪声ξ(n)平方和为
ξTξ=(yT-Cx)(y-Cx)
(11)
结合式(10)、(11),为平衡非一致项ε(n)、非阶比分量、背景噪声ξ(n)所占比例及对结果影响,引入加权因子,r(n)可决定滤波器跟踪特性。
J=r2εTε+ξTξ
(12)
式中:r为加权因子。
求J对xH的一阶导数并使其为零,得
2r2ATAx+2(x-CHy)=0
(13)
求解上式得复包络x(n)为
x=(r2ATA+E)-1CHy
(14)
式中:AT,A为对称半正定矩阵;B=r2ATA+E为对称正定矩阵,其非零对角线数等于2p+1,p为滤波器极点数。
对矩阵B做Cholesky分解,即B=LLT=LU, L为下三角形矩阵,U为上三角矩阵,则Bx=y可表示为LU=y,化为
Lz=y,Ux=z
(15)
由式(15)可求出z=L-1y,进而获得x=U-1z。Cholesky 分解优势在于非零元素(含对角线元素)所占带形最大宽度即半带宽为p+1。线性方程组(15)可通过向前分解、向后代入逐个求出未知解。
1.3与传统方法原理对比
传统起停车分析方法中常用短时傅里叶变换与内插技术求出各时窗内信号幅值、频率、相位,获得到起停车过程Bode图。STFT一般表达式为
Sx(ω,t)=∫x(τ)m(τ-t)e-jωτdτ
(16)
最基本假设即将较短的非平稳信号视为短时窗内平稳信号,而起停车信号频率、幅值均非恒定,利用STFT求频率幅值相位时会产生频率模糊、幅值相位失真等现象。对计算阶比方法而言,虽经等角度采样转化实现频率平稳,但幅值仍为变化的,若再通过FFT计算各阶次幅值相位,仍存在平均效应引起的误差,使幅值、相位不准确。而Vold-Kalman跟踪的阶比分量通过滤波过程实现,且不会发生相位偏移。所提阶比分量由复包络与载波乘积表示,可通过复包络直接求出各转速下振幅及相位,完全摆脱FFT的平均效应,使幅值、相位精度更高。
2转子典型故障特征提取研究
在Bently RK4转子实验台上验证本文方法,模拟不对中及转子裂纹故障,采集起停车信号,进行Vold-Kalman滤波提取1~4阶阶比分量,并绘制全息瀑布图。为充分考虑转子支撑各向异性影响,分别在A、B两测量面安装相互垂直的电涡流传感器,实验台结构及传感器安装方式见图1。
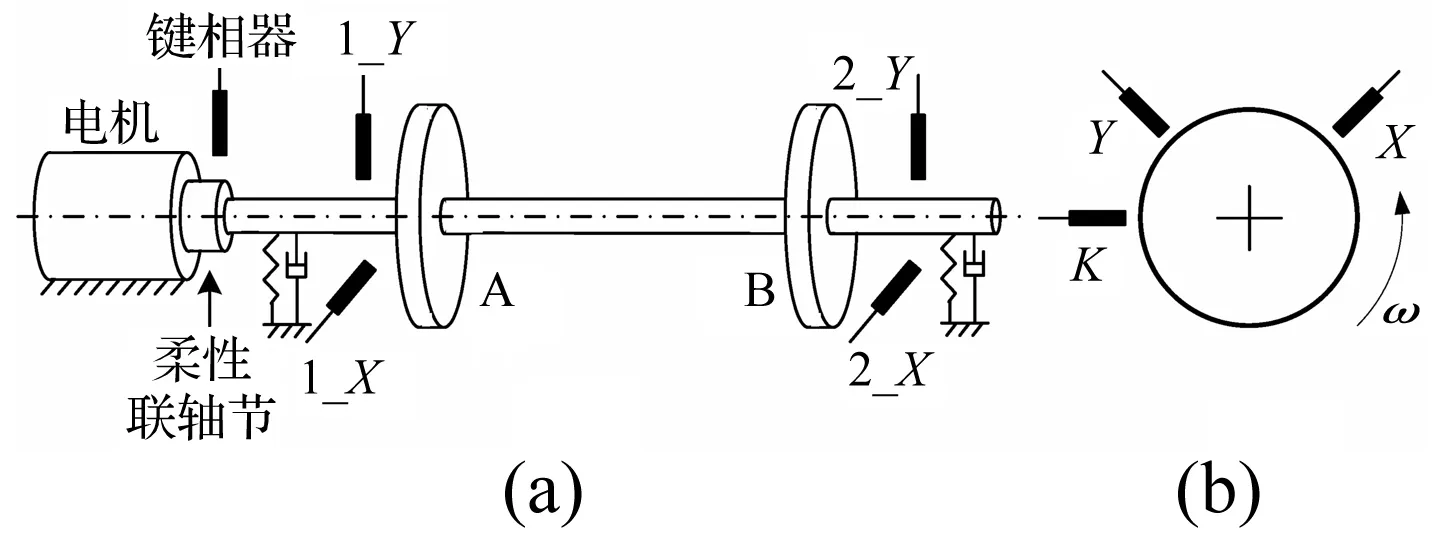
图1 传感器安装示意图Fig.1 Schematic diagram of sensor installation
采样频率2 048 Hz,时长80 s,选合适的升速比,用DT9837B数采卡对转子起停车数据连续采集,测量转子系统在0~4 000 r/min范围内的起停车数据。获得试验台振动数据后按基于VKF阶比全息的转子启停机故障特征提取流程进行故障特征提取,获得阶比全息瀑布图。故障特征提取流程见图2。
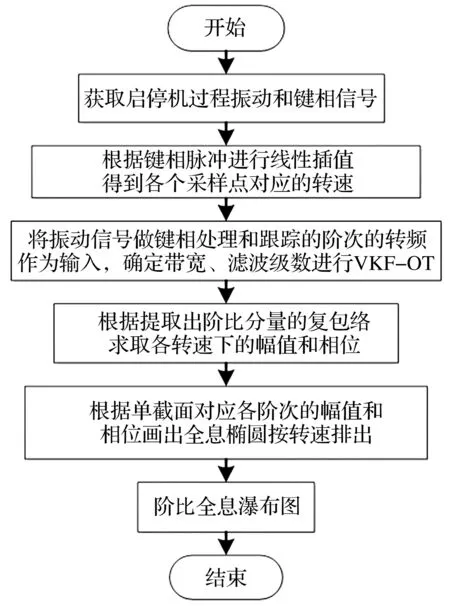
图2 基于VKF阶比全息的转子启停机故障特征提取流程Fig.2 Rotor fault feature extracting procedure based on VKF method
2.1不对中故障
在Bently转子动平衡实验台上将电机侧用垫片垫高,进行不对中故障模拟,用DT9837B对转子启停机过程进行连续数据采集,以采样频率FS=2048 Hz采集转速从200 r/min升速到5 500 r/min的启停机数据,绘制阶比全息瀑布图见图3。由图3看出,转子不对中故障主要特征为:①1、2阶分量较大;② 1阶椭圆偏心率较大;③ 2阶随转速变化;④ 2阶存在亚临界共振。
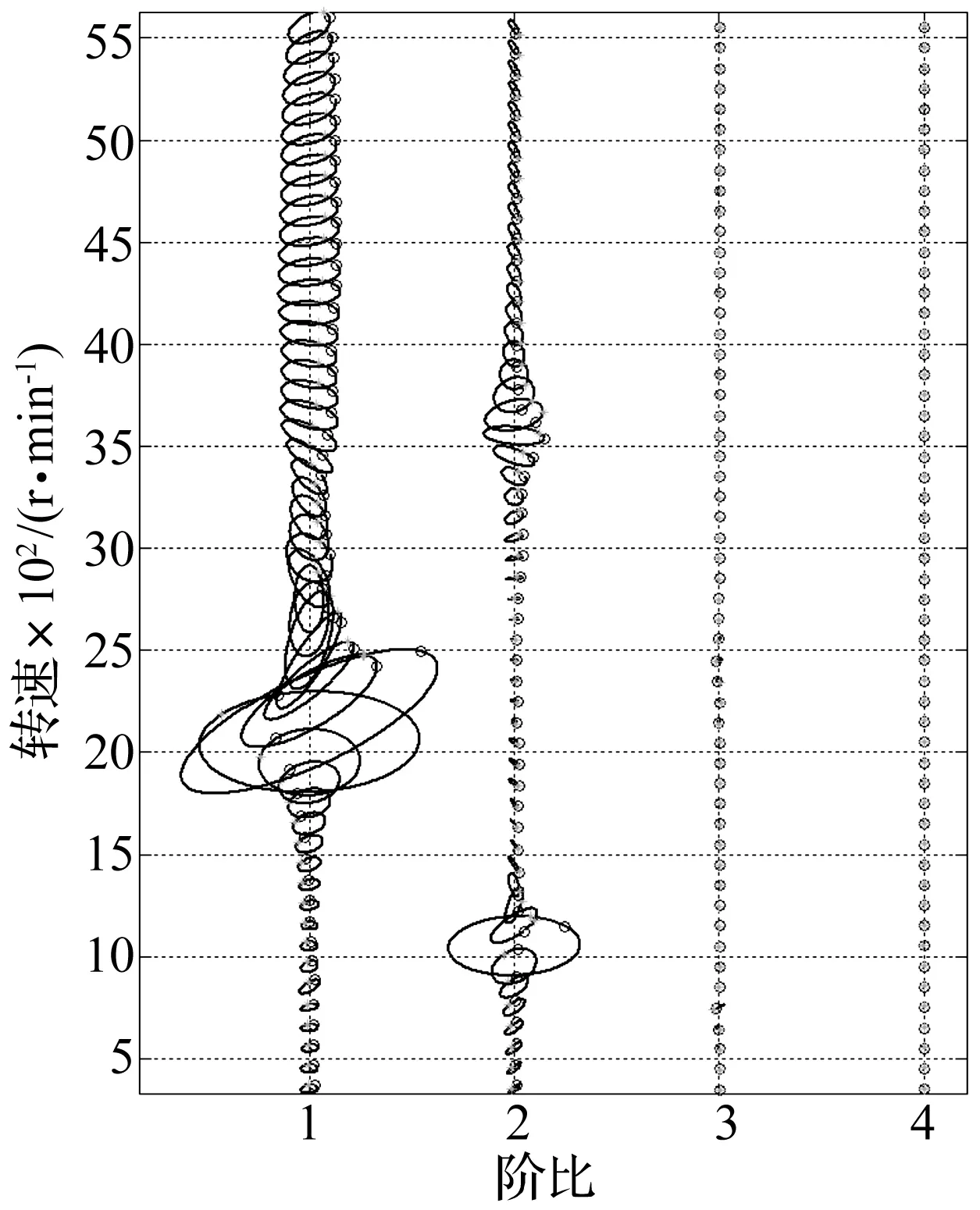
图3 不对中故障阶比全息瀑布图Fig.3 Order Tracking Holo-waterfall plot of misalignment fault
2.2裂纹故障
在轴中部加工裂纹转子,大小约1/4转子直径,在Bently转子动平衡实验台进行转子裂纹故障模拟。用DT9837B对转子启停过程连续数据采集,以采样频率FS=2 048 Hz采集转速从200 r/min升速到5 500 r/min的数据,绘制阶比全息瀑布图见图4。由图4看出,转子裂纹故障主要特征为:① 有较大的2、3阶分量;② 1阶与不平衡相近;③ 临界区椭圆翻转较慢;④ 出现2、3阶亚临界共振,振幅变化不大。
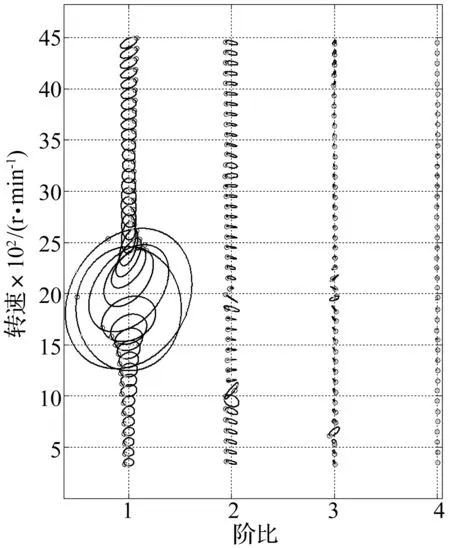
图4 裂纹故障阶比全息瀑布图Fig.4 Order Tracking Holo-waterfall plot of crack fault
通过两种模拟故障的阶比全息瀑布图,总结出了转子典型故障的特征,可见通过VKF-OT与全息谱结合可以很好地突出故障的特征,为对转子故障的识别提供了新的思路。
3起车瞬态动平衡方法研究
基于Vold-Kalman阶比全息方法,利用其对转子不平衡故障特征提取,在Bently转子实验台上进行一二
临界间力与力偶同时平衡实验。在平衡的Bently转子试验台上模拟力偶不平衡,左盘模拟重量、方位为0.4 g∠0°,右盘模拟重量、方位为0.8 g∠90°。模拟力、力偶不平衡状态作为原始起车,在左盘加0.4 g∠45°试重,右盘加0.4 g∠0°试重,并起车。两次起车采样频率均2 048 Hz。
用3阶Vold-Kalman滤波器,带宽选3对键相后原始起车、试重起车分别提取1阶,滤波获得1阶分量的复包络、载波,通过求复包络幅值、相位获得各转速下键相槽对准键相传感器时左右两盘X、Y方共4个传感器的8路信号伯德图。见图5~图10。图5、图6为原始起车两截面4个传感器振动信号伯德图,图7~图12为试重起车两截面4个传感器振动信号伯德图。
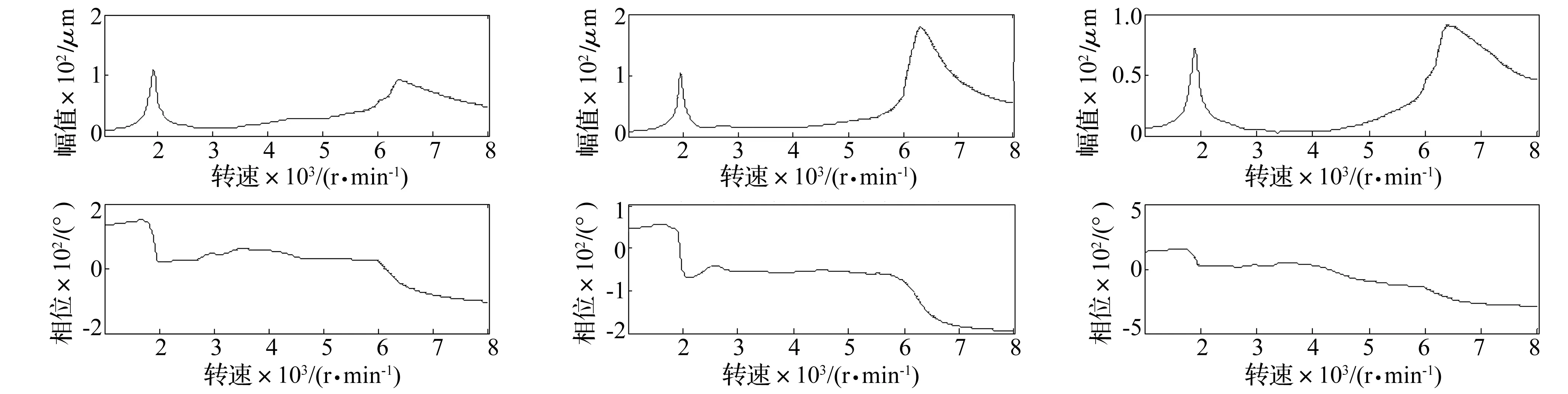

图5 原始1XFig.5Original1Xplot图6 原始1YFig.6Original1Yplot图7 原始2XFig.7Original2Xplot

图8 原始2YFig.8Original2Yplot图9 试重1XFig.9Testingweight1Xplot图10 试重1YFig.10Testingweight1Yplot

图11 试重2XFig.11 Testing weight 2X plot
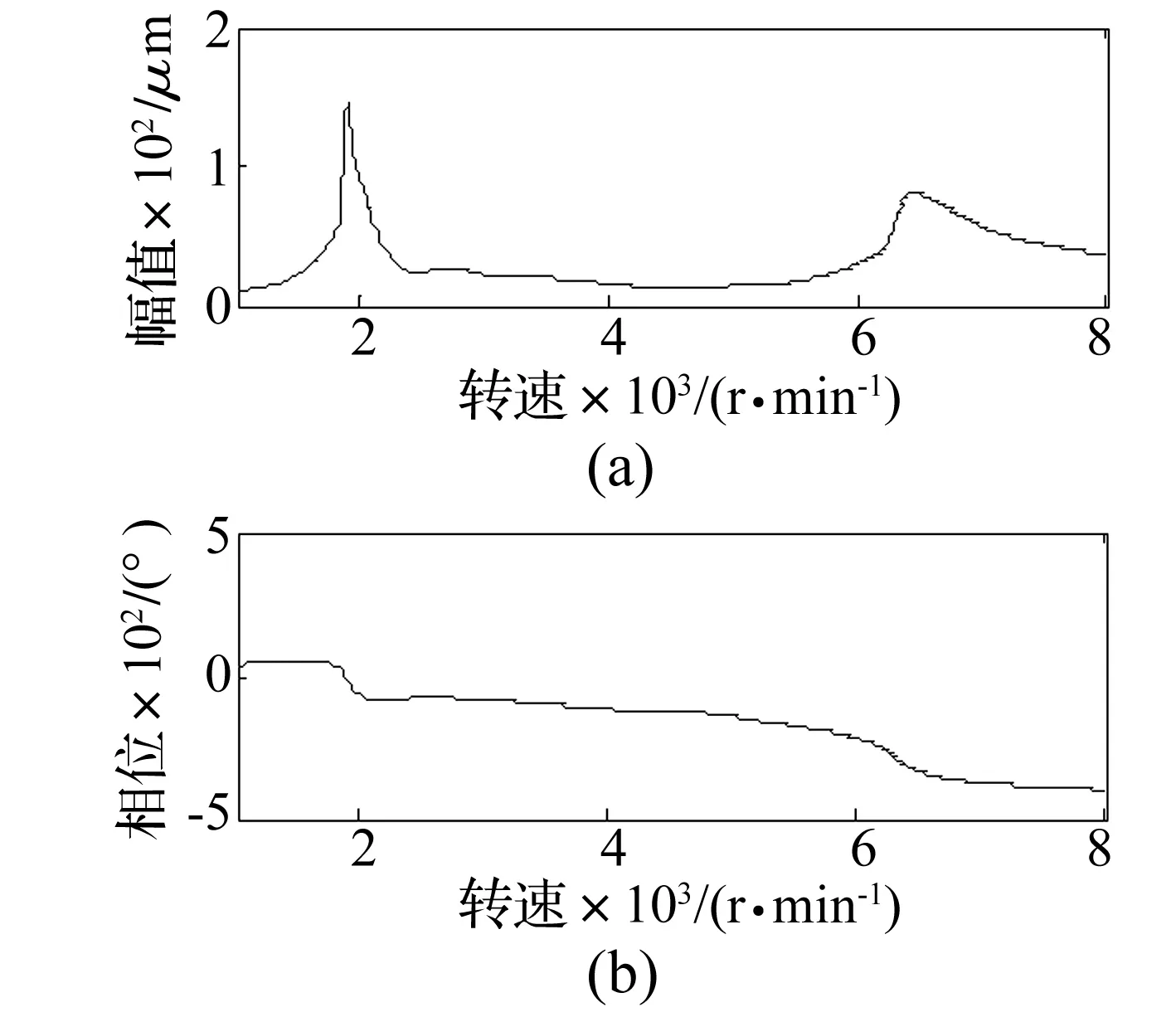
图12 试重2YFig.12 Testing weight 2Y plot
在一二临界间分别选转速3 000 r/min、4 000 r/min、5 000 r/min时原始与试重起车4通道对应的幅值、相位进行平衡配重计算,结果见表1。由表1看出,3转速下均能降低振动,但5000 r/min时平衡效果最好。因此,通过Vold-Kalman阶比跟踪与全息动平衡技术结合对转子起车过程进行动平衡可行,平衡效果较好。
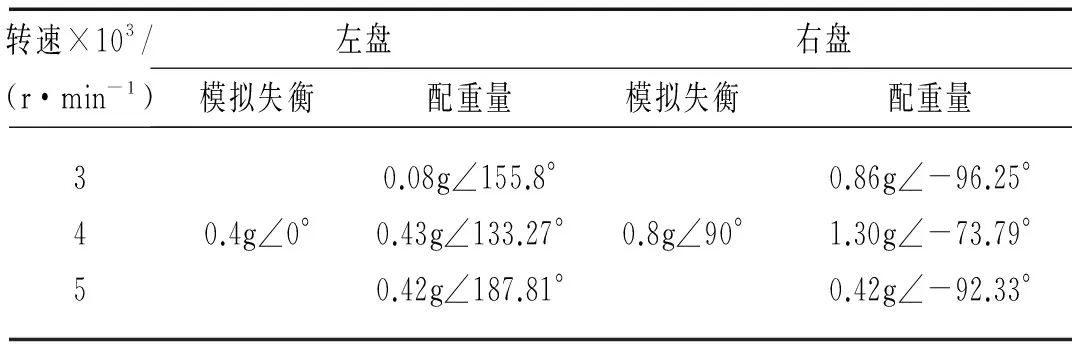
表1 动平衡配重计算对比
4结论
(1) 利用Vold-Kalman阶比跟踪方法结合全息谱分析研究转子起停车过程故障特征提取方法,提出基于VKF-OT结合全息谱技术的阶比全息瀑布图法进行转子故障特征提取方法及基于VKF-OT复包络的起停车瞬态动平衡方法,并实验验证。
(2) 本方法不仅能提取转子典型故障特征,且能有效进行起停车瞬态动平衡。较传统的短时傅里叶变换方法,阶比跟踪技术能提取起停车过程振动信号中各阶分量,且能保留瞬变信息,为起停车故障特征提取及动平衡方法研究提供新的有效途径。
参 考 文 献
[1] 韩捷,张瑞林. 旋转机械故障机理及诊断技术[M]. 北京:机械工业出版社,1996.
[2] 孙惠国,张瑞林. 设备状态监测与故障诊断[M]. 郑州:河南科学技术出版社,1992.
[3] 纪月波,郭瑜. 阶比分析技术的发展应用与展望[J]. 现代制造工程,2007,11:123-126.
JI Yue-bo, GUO Yu. The application and prospect of order analysis technology[J].Modern Manufacturing Engineering, 2007, 11:123-126.
[4] 赵晓平,张令弥,郭勤涛. 旋转机械阶比跟踪技术研究进展综述[J].地震工程与工程振动,2008,28(6):213-219.
ZHAO Xiao-ping, ZHANG Ling-mi, GUO Qin-tao. Advances and trends in rotational machine order tracking methodology[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(6):213-219.
[5] Wang Ke-sheng. Approaches to the improvement of order tracking techniques for vibration based diagnostics for in rotating machines[D]. South Africa:University of Pretoria,2010.
[6] Bossley K, Mckendrick R J. Hybrid computed order tracking [J]. Mechanical Systems and Signal Processing,1999,13(4):627-641.
[7] Vold H, Leuridan J. High resolution order tracking at extreme slew rates, using Kalman tracking filters[C]//SAE Technical, Noise & Vibration Conference & Exposition, Traverse City, Michigan, 1993:931288.
[8] Pan Min-chun,Wu Cheng-xue. Adaptive angular displacement Vold-Kalman order tracking[J]. Mechanical Systems and Signal Processing, 2007, 21:2957-2969.
[9] 屈梁生. 机械故障的全息诊断原理[M]. 北京:科学出版社,2007.
[10] 屈梁生,张西宁,沈玉娣. 机械故障诊断理论与方法[M]. 西安:西安交通大学出版社,2009.
[11] 傅炜娜. 基于Vold-Kalman跟踪滤波的旋转机械阶比分析方法研究[D]. 重庆:重庆大学, 2010.
[12] 赵小平. 旋转机械阶比分析研究与软件实现[D].南京: 南京航空航天大学, 2008.
基金项目:国家自然科学基金项目(51365051);国家自然科学基金资助项目(51421004);教育部新世纪优秀人才支持计划(NCET-13-0461);中央高校基本科研业务费专项资金资助
收稿日期:2014-10-28修改稿收到日期:2015-01-20
中图分类号:TH17
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.02.011
Fault feature extraction from the vibration signals in rotor start-up or slowdown processes based on order tracking and holospectrum
WEN Guang-rui, JIANG Cheng, LI Yang, LIAO Yu-he
(The State Key Laboratory for Manufacturing Systems, Xi’an Jiaotong University, Xi’an 710049, China)
Abstract:The vibration signal in start-up or slowdown processes can be regarded as a dynamic response to a wide frequency range excitation, which contains more information than steady state vibration signals. So it deserves more attention to extract fault feature from the signals collected in the start-up or slowdown processes of a rotor system. Aiming at the defect that a conventional start-up or slowdown process analysis applying STFT to get vibration amplitude and phase will usually lose transient information, a method based on Vold-Kalman filtering order tracking (VKF-OT) and holospectrum was proposed. By the method, the vibration amplitude and phase can be obtained directly from the complex envelop of each order component, so they can preserve the transient information well and get rid of the average effect of STFT. The amplitudes and phases of the vibrations in two perpendicular directions at a rotor section were measured and a holo-watefall curve was plotted according to the holospectrum theory. On this basis, the fault feature extraction and transient balancing can be fulfilled. The experiment results show that the method can extract the typical fault features of the rotor and the transient balancing can also be well achieved.
Key words:rotor; run-up and shutdown; Vold-Kalman order tracking; holo-waterfall curve; fault feature extraction; transient balancing
第一作者 温广瑞 男,博士后,教授,1976年7月生

