多管火箭变射序变射击间隔发射技术研究
唐文兵, 芮筱亭,王国平, 王广伟
(1.南京理工大学 发射动力学研究所,南京 210094; 2.白城兵器试验中心,吉林 白城 137001)
多管火箭变射序变射击间隔发射技术研究
唐文兵1, 芮筱亭1,王国平1, 王广伟2
(1.南京理工大学 发射动力学研究所,南京210094; 2.白城兵器试验中心,吉林 白城137001)
摘要:应用多体系统传递矩阵法,建立了某多管火箭系统动力学模型、动力学模型拓扑图、总传递方程、特征方程及动力学数值仿真系统,对比了不同工况下多管火箭系统动态特性;设计了射序和射击间隔联合优化连续变量,结合遗传算法,实例进行了以不同工况下最佳射击密集度为目标的最佳射序和最佳射击间隔优化设计,仿真结果表明,射击密集度提高了30%以上;基于单片机技术,研制了不同工况下自适应发火装置,取得了良好的工程应用效果,实现了多管火箭变射序变射击间隔发射技术。
关键词:多管火箭;多体系统传递矩阵法;遗传算法;变射序;变射击间隔;自适应发火装置;射击密集度
多管火箭因射速快、射界大、射程远、机动性好、能在短时间内较大面积上形成强大火力密度,从而受到国际广泛重视[1]。然而,射击密集度差一直制约着多管火箭发展,是研究者长期竞相攻关研究的国际难题。
多体系统动力学相关理论经近几十年的发展,已成为复杂机械系统动力学计算、分析和设计的重要手段,极大地推动了兵器、船舶、航空、航天、交通等现代工业的发展,取得了许多科技成就,为近代科学技术作出了重大贡献。众多学者研究了多管火箭系统动力学以提高其射击密集度[1-8],芮筱亭等[5-8]深入研究了优化射序、射击间隔以改善多管火箭系统动态特性,提高射击密集度。事实上,由于不同射角和射向下多管火箭系统结构参数分布不同、不同地面条件下多管火箭系统与地面接触刚度不同,从而不同工况下多管火箭系统振动特性不同,固定射序和射击间隔下多管火箭系统难以达到最佳射击密集度。因此,为获得多管火箭系统不同工况下最佳射击密集度,不同工况下应采用不同的射序和射击间隔优化方案,进行变射序变射击间隔发射。
遗憾的是,至今尚未见变射序变射击间隔技术实际运用的报道,其原因在于,缺乏高效的多体系统动力学快速计算理论与技术,难以实现多管火箭如此复杂机械系统的动力学快速计算,是多管火箭系统动力学设计亟待解决的关键难题。通常动力学方法计算多管火箭多体系统动力学,不仅面临系统矩阵阶次高计算速度远不能满足工程设计要求的困难,而且难以避免特征值问题计算病态导致的计算失败。并且由于刚体与柔体之间的耦合作用,使得多体系统的特征值问题非自共轭,系统特征矢量不具有通常意义下的正交性,难以用经典的模态方法精确分析多管火箭多刚柔体系统的动力响应问题。
近20年逐步发展起来的多体系统传递矩阵法[9-14],作为多体系统动力学的一种全新方法,因具有无需建立系统总体动力学方程、程式化程度高、系统矩阵阶次低、计算速度快等特点,为多体系统动力学研究提供了强有力的手段。多体系统传递矩阵法因系统矩阵阶次很低而避免了复杂线性多体系统特征值问题计算病态,通过引入多体系统增广特征矢量和增广算子[9-11]的新概念及其程式化的构造方法,解决了多体系统特征矢量的正交性和响应的精确分析难题;通过建立多体系统总传递方程自动推导定理[14],实现了多体系统总传递方程的自动推导;多体系统传递矩阵法因大大简化了复杂机械系统动力学求解过程,大幅提高了计算效率,从而得到了广泛的工程应用,为研究和解决复杂多管火箭系统动力学设计问题奠定了理论基础。
本文应用多体系统传递矩阵法,建立了某多管火箭系统动力学模型、动力学模型拓扑图及动力学数值仿真系统,突破多管火箭系统动力学设计快速计算的关键技术;设计了射序和射击间隔联合优化连续变量,结合遗传算法,进行了以不同工况下最佳射击密集度为目标的多管火箭射序、射击间隔优化设计,实例得到了最佳射序和最佳射击间隔方案,仿真结果表明,射击密集度提高了30%以上,是低成本提高多管火箭射击密集度的有效途径;以此为基础,研制了不同工况下自适应发火装置,取得了良好的工程应用效果。
1多管火箭系统动力学模型
图1所示为某多管火箭系统三维实体模型,根据多管火箭系统各大部件的自然属性,应用多体系统传递矩阵法,将其分解为体元件和铰元件,体元件包括集中质量、刚体、弹性梁等,铰元件包括扭簧、弹簧、阻尼器等,“铰”不计质量,其质量全部归入相邻的“体”中。将任一瞬时多管火箭系统中除去已击发火箭弹和最新击发火箭弹所在定向管的起落部分简称起落部分,除去俯仰部分的回转部分简称回转部分,除去车轮的汽车底盘和底架简称车体,最新击发火箭弹所在定向管尾部简称定向管尾,上述部件及车轮或千斤顶视为各具有6个自由度的刚体;最新击发火箭弹所在定向管简称定向管并视为空间运动弹性梁;定向管与起落部分之间的作用、高低机和平衡机的作用以及回转部分与起落部分的弹性和阻尼效应、方向机的作用以及车体的弹性和阻尼效应、车轮或千斤顶的弹性和阻尼效应及与地面的作用、摇架与定向管间的联接等,分别用反映3个方向相对角运动的扭簧和反映3个方向相对线运动的弹簧及与之并联的阻尼器来等效。

图1 某多管火箭系统三维实体模型Fig.1 The 3D solid model of the MLRS
建立的多管火箭系统动力学模型如图2所示,体元件和铰元件统一编号。元件1, 3, 4, 6, 7, 9, 10, 12, 13, 15, 16, 18, 20, 22,24+5l,25+5l为弹性铰;元件2, 5, 8, 11, 14, 17, 19, 21, 23,26+5l为刚体;元件27+5l,28+5l为弹性梁。l(l=1,2,…,18)为正在击发火箭弹所在定向管编号,系统共有8个边界点,并编号为0。多管火箭系统动力学模型即为:在地面支撑作用下,由各种弹簧、扭簧、阻尼器联接的28个刚体、18个弹性体组成的多刚柔体系统。
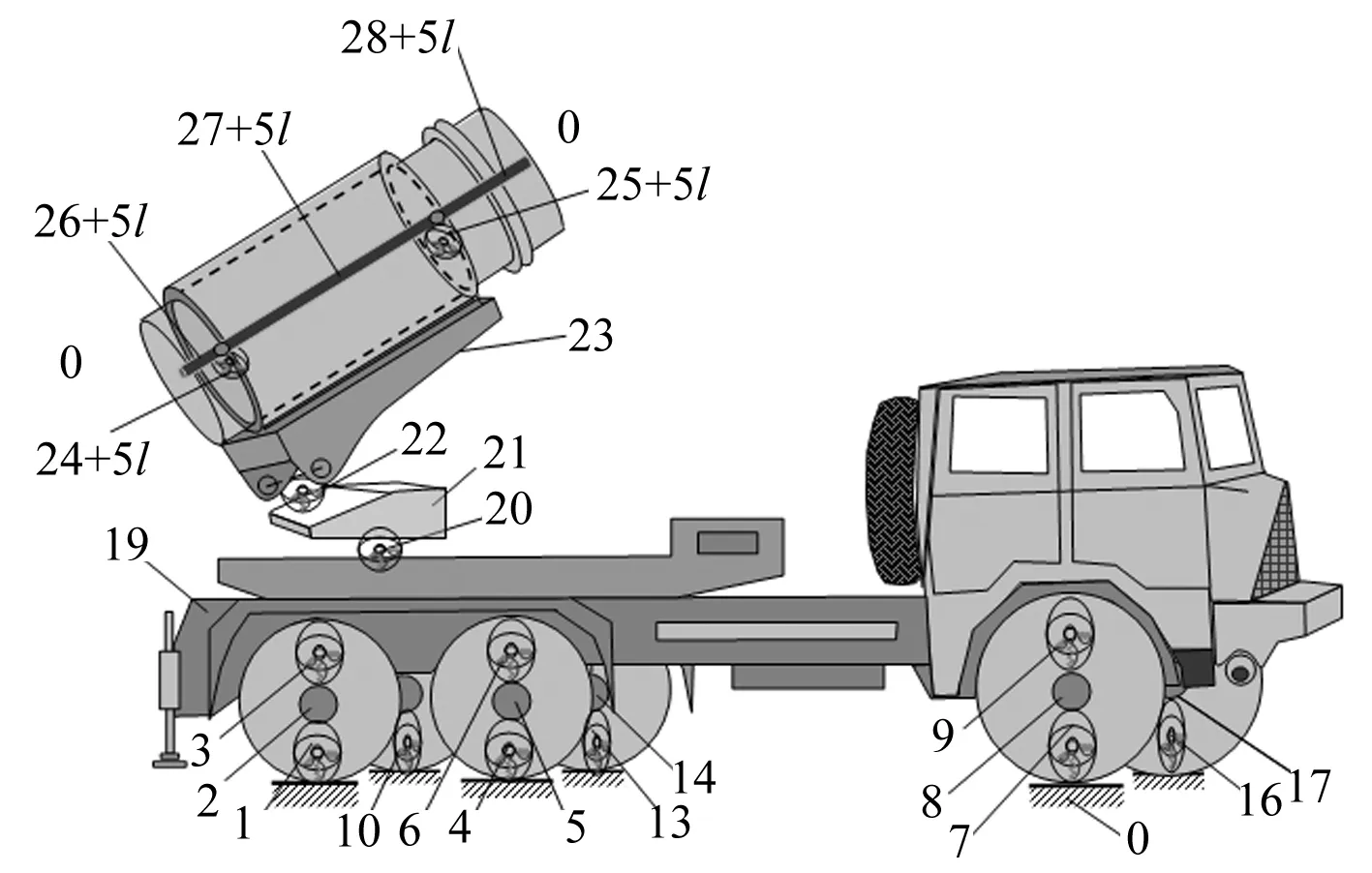
图2 多管火箭系统动力学模型Fig.2 Dynamics model of MLRS
2多管火箭系统动力学模型拓扑图
根据多体系统传递矩阵法和多管火箭系统动力学模型,建立多管火箭系统动力学模型拓扑图,如图3所示。多体系统动力学模型的拓扑图是多体系统传递矩阵法中描述元件状态矢量间关系和传递方向的新的图示方法[14]。根据多体系统传递矩阵法符号约定,拓扑图中圈表示体元件,圈中数字表示体元件序号;箭头表示铰元件,箭头指向为传递方向,箭头旁的数字表示铰元件序号;对含有两个联接点的体元件视为一端输入一端输出元件,含有两个以上链接点的体元件视为多端输入一端输出元件;对非边界端状态矢量Zi,j,第一个下标i为体元件序号,第二个下标j为铰元件序号;对边界端状态矢量Zi,j,第一个下标i为边界元件的序号,第二个下标j=0,表示边界端;视边界点(28+5l,0)为系统的根,其他边界点视为系统的梢,系统的传递方向为从梢到根。
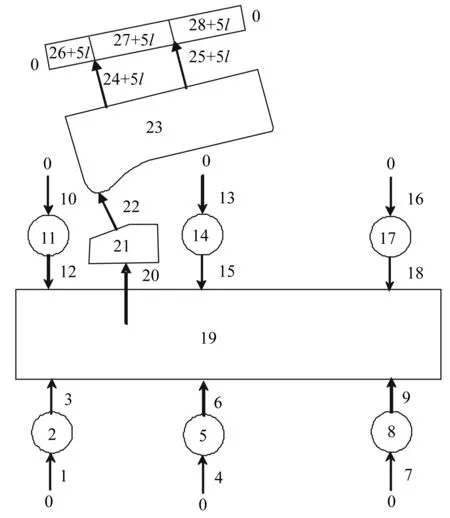
图3 多管火箭系统动力学模型拓扑图Fig.3 The topology figure of dynamics model of MLRS
3多管火箭系统总传递方程和特征方程
根据总传递方程自动推导定理[14]和多管火箭系统动力学模型拓扑图,可自动列写多管火箭系统总传递方程如下
UallZall=0
(1)
式中:
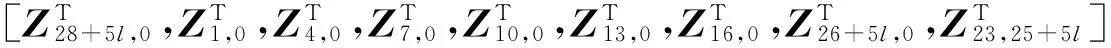
Uall为总传递矩阵,Z23,25+5l表示系统闭环子系统中体元件23与铰元件25+5l联接点处的状态矢量,Zi,0(i=1,4,7,10,13,16,26+5l,28+5l)为多管火箭系统各边界点状态矢量;O为零元素,I12为12阶单位矩阵;Ti-28+5i(i=1,4,7,10,13,16,23,25+5l,26+5l)表示从系统梢点Zi,0到根Z28+5l,0的路径上所有元件传递矩阵的依序连乘积;Gi-j(i=1,4,7,10,13,16,23,26+5l;j=19,23,27+5l,28+5l)表示从元件j到系统梢Zi,0的路径上所有元件传递矩阵的依序连乘积,再左乘(-Hj,1)(若k=1)或左乘Hj,k(若k=2,…,L),k为元件j的输入端编号;各元件的传递矩阵推导过程及具体形式参见文献[9,14]。

(2)
则多管火箭系统特征方程为
(3)
求解式(3)可得到系统的固有振动频率ωk(k=1,2,3…n)。
在多体系统传递矩阵法中,为了描述系统运动的方便,根据研究对象建立若干个方位不同的惯性坐标系,各坐标系之间的方位关系用方向余弦矩阵描述。当多管火箭射角为θ,射击方向角为α时,按传递方向,联接点i21(21,20)和i23(23,22)的状态矢量需先后通过坐标变换
Z21,20=HαZ′21,20
(4)
Z23,22=HθZ′23,22
(5)
转换后进行传递,其中
与地面联接的铰元件1、4、7、10、13、16的传递矩阵U1、U4、U7、U10、U13、U16形式为
(6)
式中:
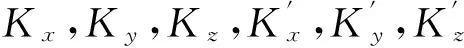
因此,射角、射向以及地面条件的改变均会引起总传递矩阵Uall中参量的变化,从而系统振动特性不同。
4多管火箭系统动力学仿真
4.1多管火箭发射与飞行动力学数值仿真系统
文献[1]对多管火箭发射动力学、飞行动力学以及数值仿真方法等进行了深入的研究,本文限于篇幅,不再详细列出讨论,结合本文多管火箭系统动力学模型,建立多管火箭系统动力学数值仿真系统,仿真流程如图4所示。
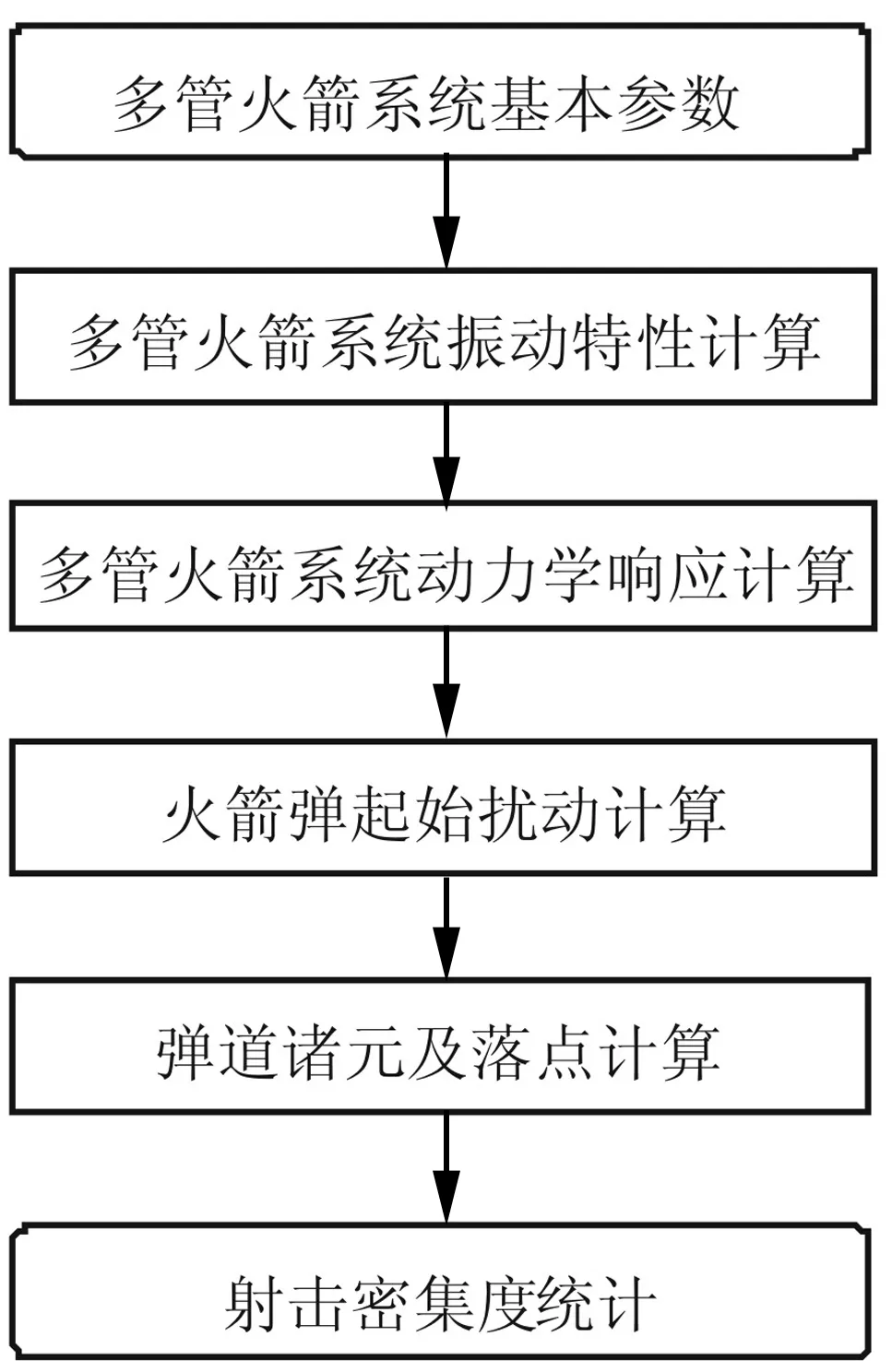
图4 多管火箭系统动力学仿真流程Fig.4 The flow chart of dynamics simulation
4.2不同工况下多管火箭系统动态特性
以4个工况为例,工况1表示水泥地面,射角50°,射向0°;工况2表示水泥地面,射角30°,射向0°;工况3表示水泥地面,射角50°,射向45°;工况4表示泥土地面,射角50°,射向0°。表1给出了满载多管火箭系统在上述4种工况下的前6阶固有频率,射击过程中多管火箭定向管口的位移响应如图5,图6所示,可见,不同工况下多管火箭系统动态特性有较大差异。
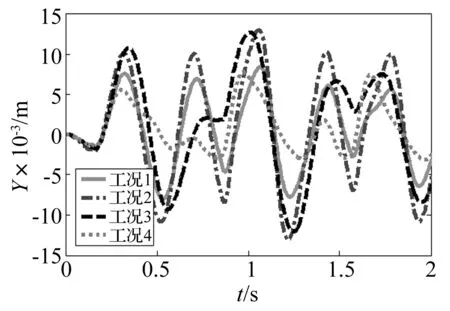
图5 Y方向位移响应Fig.5 Displacement responds along Y direction
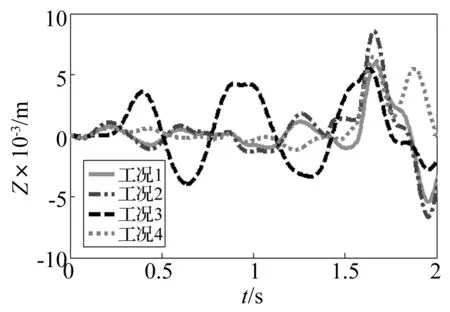
图6 Z方向位移响应Fig.6 Displacement responds along Z direction
起始扰动是影响射击密集度的最主要因素[1],多管火箭系统动态特性的差异对射击密集度的影响都通过并只有通过起始扰动来反映,表2给出了相同射序和射击间隔方案不同工况下火箭弹起始扰动,可见,不同工况下火箭弹起始扰动有明显差异。因此,在不同工况下,可通过变射序变射击间隔发射来改善多管火箭系统动态特性,获得最佳射击密集度。
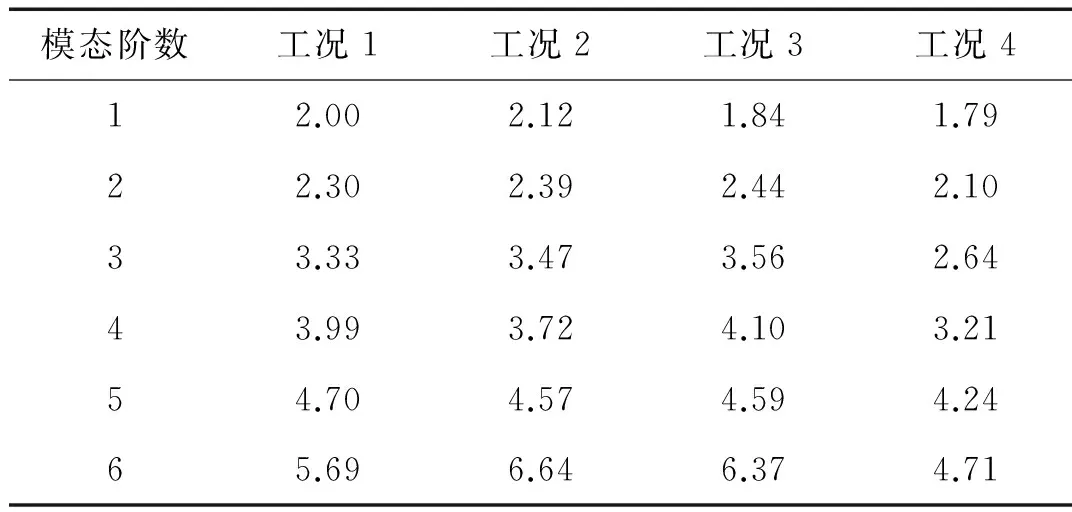
表1 满载多管火箭系统不同工况固有频率(Hz)
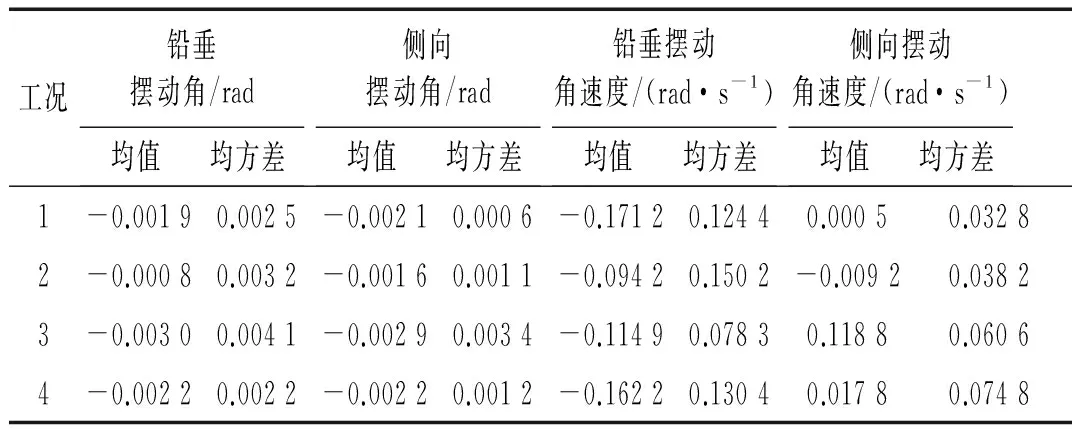
表2 不同工况火箭弹起始扰动
5多管火箭射序和射击间隔优化设计
5.1射序和射击间隔联合优化设计
射序不仅是位置空间内的离散量,同时也对应相应定向管内的火箭弹被击发时刻。以时间为统一量,射序和射击间隔组成一条连续且完整的射击时间轴。
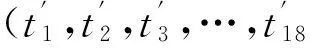
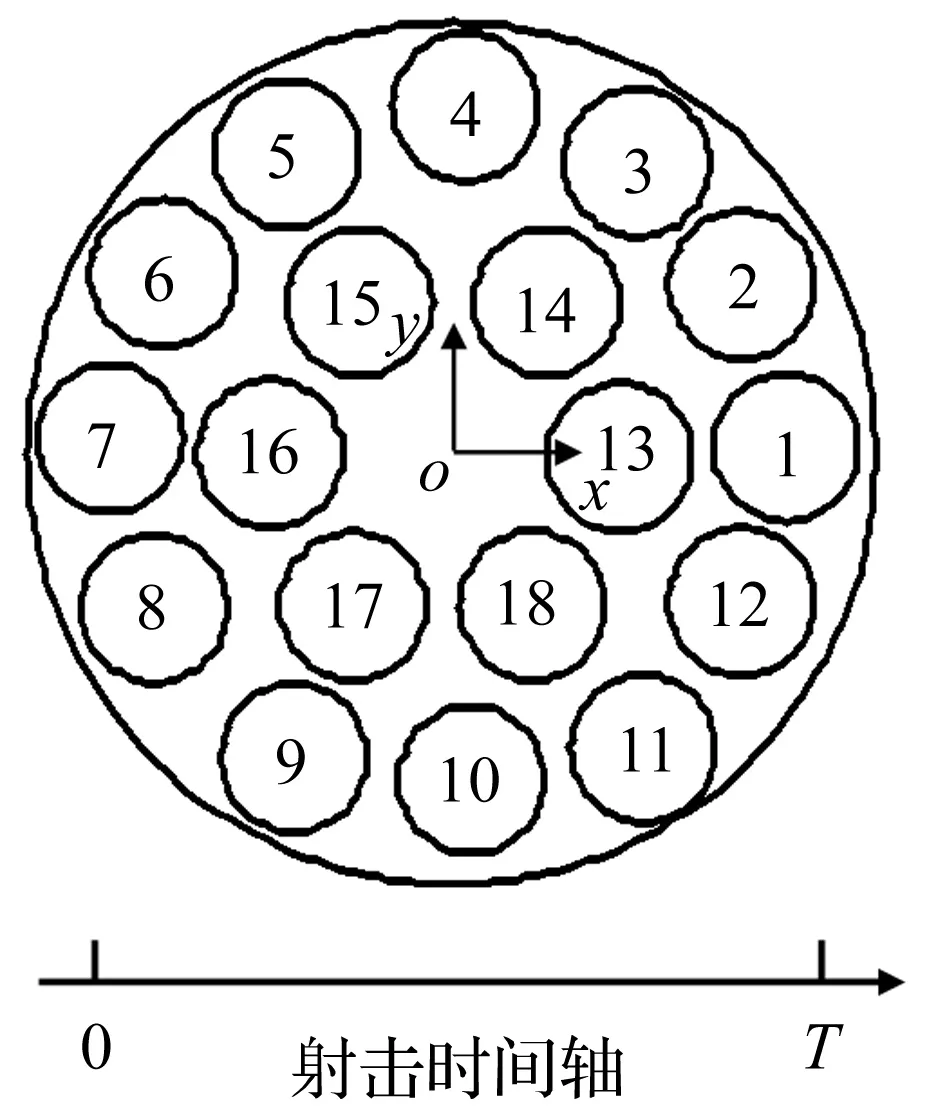
图7 定向管编号方案Fig.7 Numbering scheme of launch tubes
以多管火箭齐射落点的圆概率误差为目标函数,构造含有约束条件的最优化问题
(7)
式中:Ex,Ez分别为落点纵向和横向密集度;约束条件要求一轮齐射过程在Ts内完成,相邻两发火箭弹射击间隔大于t0s。
5.2遗传算法优化流程
应用多管火箭发射与飞行动力学数值仿真系统,结合遗传算法[15],对设计变量进行选择、交叉、变异等遗传操作,进行不同工况下多管火箭射序和射击间隔优化,优化设计流程如图8所示。
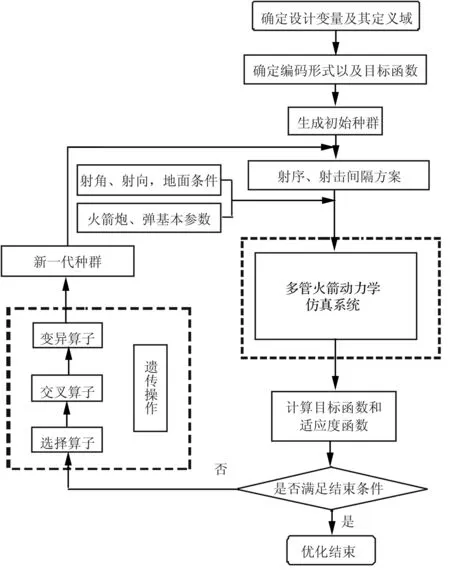
图8 射序和射击间隔优化设计流程Fig.8 The flow chart of optimization
遗传算法主要操作过程如下:
(1) 编码:将设计变量序列(t1,t2,t3,…,t18)中每一个实数变量采用二进制编码形式表示为一个{0,1}二进制串,串长取决于求解的精度。
例如,若式(7)中T=12 s,设求解精度不小于5×10-3s,二进制编码长度为n,则区间[0,12]被等分为2n-1份,有
(8)
得到
n≥12
(9)
所以一个实数变量编码的二进制串长至少需要12位,则设计变量序列对应编码长度为18×12=216的二进制串。
(2) 产生初始种群:初始种群中包含多管火箭射序和射击间隔原方案,其余由随机产生的满足式(7)中约束条件的个体组成。由于本文最优化问题属于“高度约束”问题,对后代种群中不满足约束条件的个体采取了拒绝策略。
(3) 计算适应度:构造的最优化问题为最小问题,且CEP>0,本文构造适应度函数
Fitness(CEP)=150/CEP
(10)
(4) 选择、交叉、变异操作:选择、交叉、变异是遗传算法的三个基本操作,本文分别采用锦标赛选择算法、二进制均匀交叉算法和二进制变异算法,并设定交叉率和变异率分别为0.6和0.001。
(5) 结束条件
选取适应度函数值和遗传代数作为优化搜索结束的条件,即①Fitness(CEP)>α;②Generation>m;满足其一即停止搜索,α的选取体现了对射击密集度的预期要求,m为遗传代数。
5.3多管火箭变射序变射击间隔仿真实例
以工况1为例,将火箭炮、弹的参数以及该工况下射角、射向和地面刚度输入射序和射击间隔优化仿真系统,令式(7)中T=12 s,t0=0.3 s,即要求多管火箭12 s内一轮齐射完毕,相邻两发火箭弹点火时间间隔大于0.3 s,设置仿真结束条件为优化3 000代结束。
根据适应度函数提取每代最优个体,最优个体适应度变化过程如图9所示,对应多管火箭射击密集度变化过程如图10所示。最优个体见表3,根据5.1节射序和射击间隔联合优化设计方法,可得射序优化方案如图11所示,图中序号为射击顺序,图12为射击间隔优化方案,整个射击过程(从第1发火箭弹点火到第18发火箭弹点火)用时11.55 s。
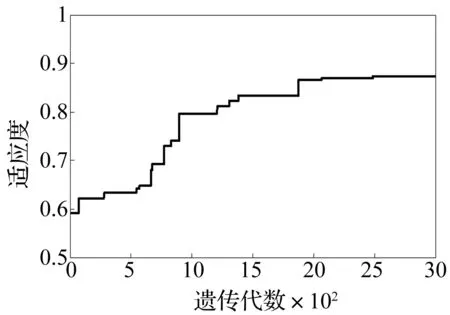
图9 适应度变化过程Fig.9 The optimization process of the fitness
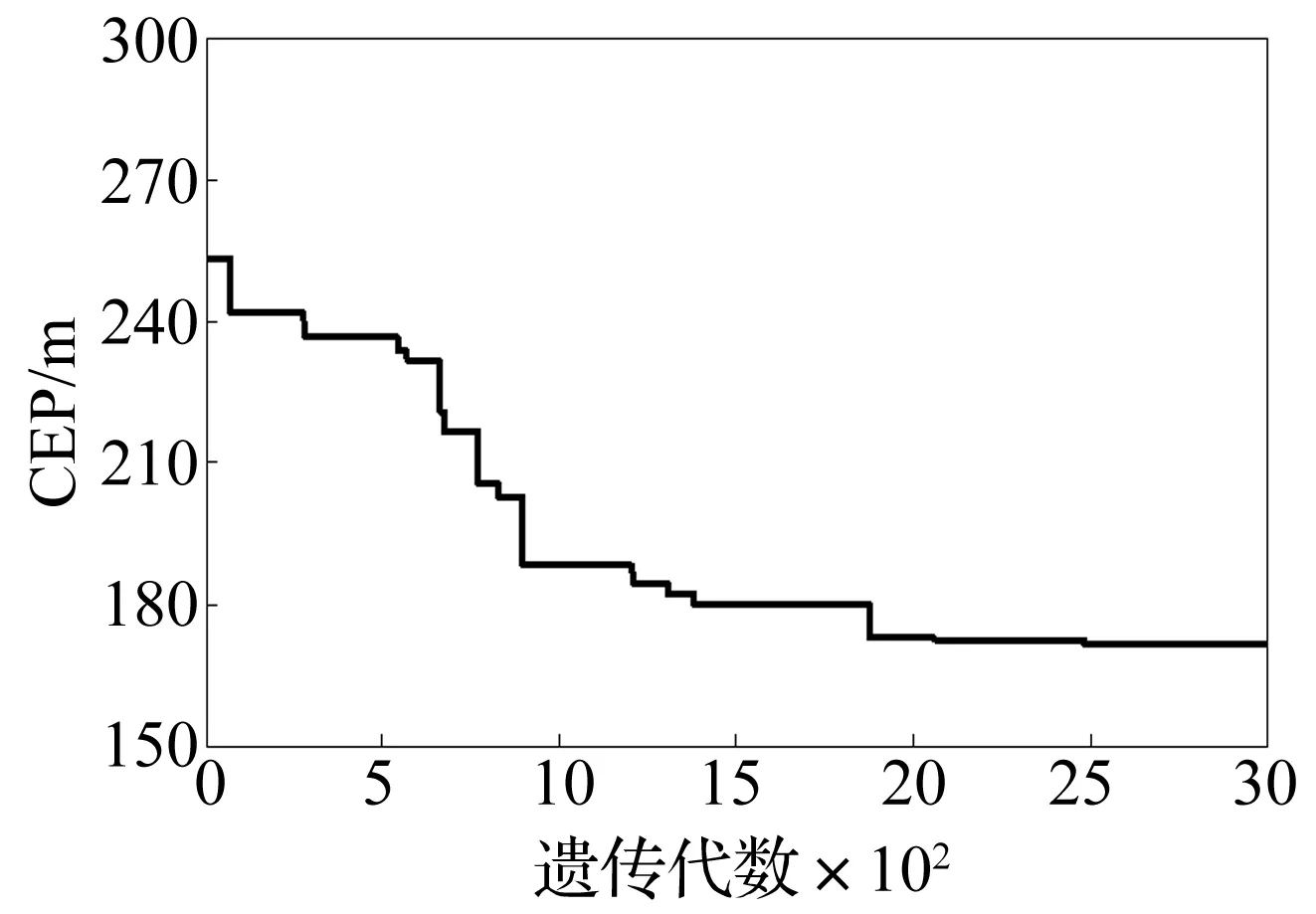
图10 射击精度变化过程Fig.10 The optimization process of the CEP

变量值变量值变量值t110.73t73.44t130.37t22.56t811.25t144.27t39.43t93.86t156.11t47.02t1011.92t167.71t50.88t115.68t171.48t65.14t128.32t186.68
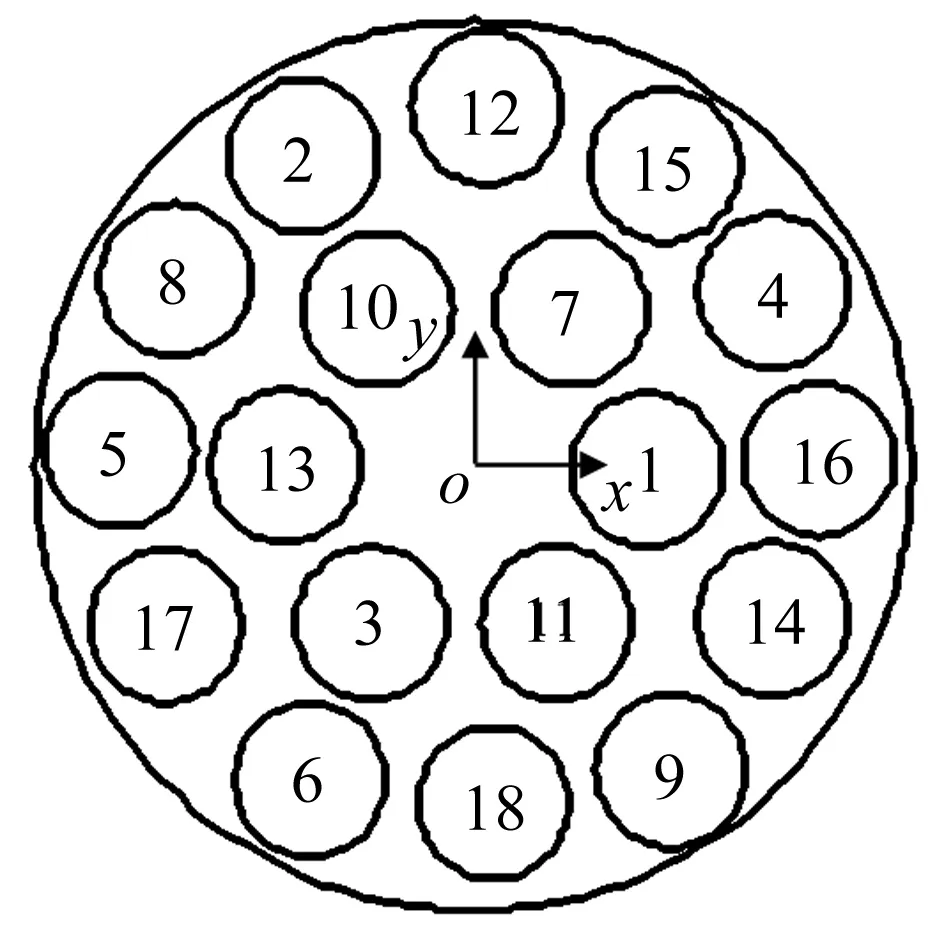
图11 射序优化方案Fig.11 The optimal scheme of firing orders
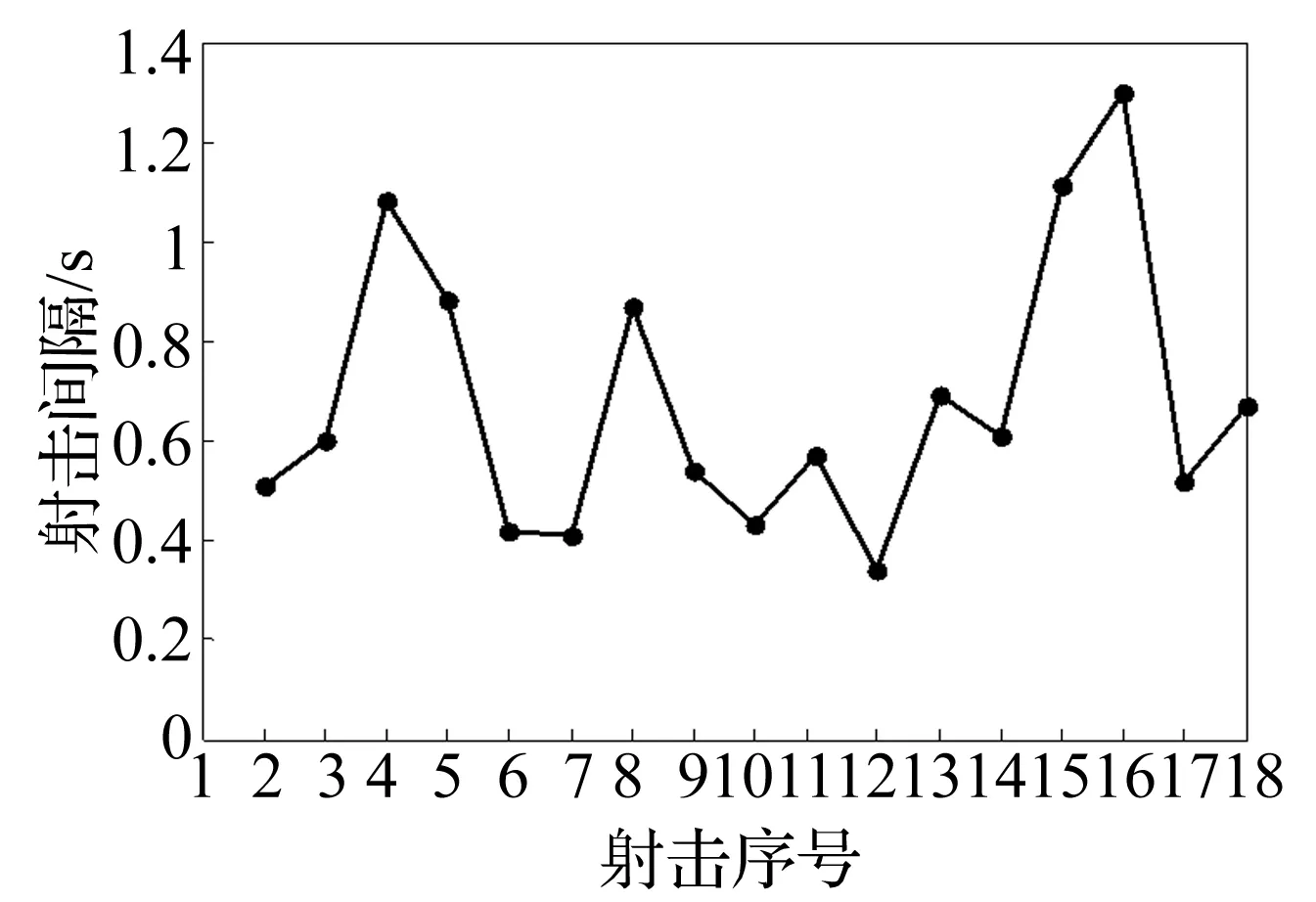
图12 射击间隔优化方案Fig.12 The optimal scheme of firing intervals
表4给出了工况1下采用射序和射击间隔原方案与优化方案的射击密集度对比结果,可见,通过变射序变射击间隔发射,实现了多管火箭系统动态特性优化,提高了多管火箭系统射击密集度32.3%。

表4 原方案与优化方案射击密集度
6自适应发火装置
基于单片机技术,研制了多管火箭不同工况下自适应发火装置,如图13所示。控制器软件通过定时中断方式和延时程序调用分别实现对射击间隔和点火脉宽的高精度控制,图14为变间隔发射信号示意图。结合变射序变射击间隔优化软件,该装置在工程应用中取得了良好的效果。


图13 自适应发火装置实物图Fig.13Theself-adaptionfiringdevice图14 变间隔发射信号Fig.14Thefiringsignalswithunequalintervals
7结论
从武器系统动力学角度出发,对多管火箭射击密集度进行动态设计已成为重要的研究和发展方向。由于不同工况下多管火箭系统动态特性存在差异,本文立足于工程应用,提出了多管火箭在不同工况下进行变射序变射击间隔发射的思想。
基于多体系统传递矩阵法和遗传算法,形成了变射序变射击间隔仿真优化软件,设计的射序和射击间隔联合优化连续变量对射序和射击间隔的优化具有重要意义,实例仿真结果表明,多管火箭射击密集度提高了30%以上;研制了自适应发火装置,实现了多管火箭不同工况下变射序变射击间隔发射技术,该技术是低成本大幅度提高射击密集度的有效途径,具有广阔的工程应用前景。
参 考 文 献
[1] 芮筱亭,陆毓琪,王国平,等.多管火箭发射动力学仿真与试验测试方法[M].北京:国防工业出版社,2003.
[2] 王松超,王惠方,于存贵. 某多管火箭炮支撑动力学分析[J]. 兵工自动化,2012, 31(3): 24-26.
WANG Song-chao, WANG Hui-fang, YU Cun-gui. Dynamic analysis the support of multiple launch rocket systems [J].Ordnance Industry Automation, 2012, 31(3): 24-26.
[3] 冯勇,马大为,薛畅,等. 多管火箭炮刚柔耦合多体发射动力学仿真研究[J].兵工学报, 2006, 27(3): 545-548.
FENG Yong, MA Da-wei, XUE Chang, et al. Simulation studies of coupled rigid and flexible multi-body dynamics for multiple launch rocket systems [J]. Acta Armamentar Ⅱ, 2006, 27(3): 545-548.
[4] 曹广群,张艳华,刘树华. 基于ADAMS的多管火箭炮动力学仿真分析[J].兵工自动化, 2009, 28(2): 32-35.
CAO Guang-qun, ZHANG Yan-hua, LIU Shu-hua. Simulation analysis for launch dynamics of multiple launch rocket system based on ADMAS [J]. Ordnance Industry Automation, 2009, 28(2): 32-35.
[5] 芮筱亭,王国平,陆毓琪,等.提高多管火箭射击密集度新技术[J]. 兵工学报, 2006, 27(2): 301-305.
RUI Xiao-ting, WANG Guo-ping, LU Yu-qi, et al. A new technology to improving firing dispersion of multiple launch rocket system [J]. Acta Armamentarii, 2006, 27(2): 301-305.
[6] 王国平,芮筱亭,陆毓琪. 射序对多管火箭性能影响[J]. 南京理工大学学报, 2004, 28(4): 364-368.
WANG Guo-ping, RUI Xiao-ting, LU Yu-qi. Influence of firing orders on performance of MLRS [J]. Journal of Nanjing University of Science and Technology, 2004, 28(4): 364-368.
[7] 于海龙,芮筱亭,王刚,等. 射序、射击间隔对”金属风暴”武器射击密集度影响[J].弹箭与制导学报, 2011, 31(1): 91-93.
YU Hai-long, RUI Xiao-ting, WANG Gang, et al. The effect of firing order and firing interval to firing dispersion by metal storm weapon [J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2011, 31(1): 91-93.
[8] 贺军义,芮筱亭,王国平,等.提高多管火箭射击密集度设计技术研究[J].振动工程学报, 2011, 24(6): 676-681.
HE Jun-yi, RUI Xiao-ting, WANG Guo-ping, et al. Design technology of improving firing dispersion of MLRS [J]. Journal of Vibration Engineering, 2011, 24(6): 676-681.
[9] 芮筱亭,贠来峰,陆毓琪,等. 多体系统传递矩阵法及其应用[M]. 北京:科学出版社,2008.
[10] Rui Xiao-ting, Wang Guo-ping, Lu Yu-qi, et al. Vibration characteristics and orthogonality of linear multibody system [C]//Proceedings of the International Conference on Mechanical Engineering and Mechanics. New York: Science Press USA Inc., 2005: 916-920.
[11] 芮筱亭,贠来峰,陆毓琪.刚弹耦合多体系统增广特征矢量及其正交性[J]. 兵工学报, 2007, 28(5): 581-586.
RUI Xiao-ting, YUN Lai-feng, LU Yu-qi. Augmented eigenvector of multibody system coupled with rigid and elastic bodies and its orthogonality [J]. Acta Armamentarii, 2007, 28(5): 581-586.
[12] Rui Xiao-ting, Wang Guo-ping, Lu Yu-qi, et al. Transfer matrix method for linear multibody system [J]. Multibody System Dynamics, 2008, 19(3): 179-207.
[13] Rong Bao, Rui Xiao-ting, Wang Guo-ping. New method for dynamics modelling and analysis on flexible plate undergoing large overall motion [J]. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn., 2010, 224(K1): 33-44.
[14] Rui Xiao-ting, Zhang Jian-shu, Zhou Qin-bo. Automatic deduction theorem of overall transfer equation of multibody system [J]. Advances in Mechanical Engineering, 2014,6:378047, 12 pages.
[15] Holland J H. Adaptation in Natural and Artificial Systems [M]. Cambridge: MIT Press, 1992.
基金项目:高校博士点基金(20133219110037);国家自然科学基金(11102089);新世纪优秀人才支持计划(NCET-10-0075)
收稿日期:2015-04-02修改稿收到日期:2015-07-04
通信作者芮筱亭 男,博士,教授,博士生导师,1956年8月生
中图分类号:TJ393
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.02.009
Launching technique with variant firing orders and variant firing intervals for multiple launch rockets system
TANG Wen-bing1, RUI Xiao-ting1, WANG Guo-ping1, WANG Guang-wei2
(1. Institute of Launch Dynamics, Nanjing University of Science and Technology, Nanjing 210094, China;2. Baicheng Ordnance Test Center, Baicheng 137001, China)
Abstract:Based on the transfer matrix method for multibody system, the dynamics model of a certain multiple launch rockets system (MLRS), the topology figure of the dynamics model, the overall transfer equation,the eigenfrequency equation,and the numerical dynamics simulation system were established. The dynamic characteristics of MLRS in different working conditions were compared. The continuous variables were designed for joint optimization of firing orders and firing intervals. Combining with the genetic algorithms, the optimal design of firing orders and firing intervals for the purpose of the best firing dispersion in different working conditions was carried out on a real example. The results of simulation show that the firing dispersion is improved by more than 30%. Based on chip microprocessor technology, a self-adaptive firing device was manufactured, which receives good achievement in engineering application. Thus, the launching technique with variant firing orders and variant firing intervals by the MLRS provided was successfully realized.
Key words:multiple launch rockets system; transfer matrix method for multibody system; genetic algorithms; variant firing orders; variant firing intervals; self-adaptive firing device; firing dispersion
第一作者 唐文兵 男,博士生,1987年10月生

