商业银行信用集中风险与经济资本测度模型研究

徐少君

(浙江理工大学经济管理学院，杭州310018)



商业银行信用集中风险与经济资本测度模型研究

徐少君

(浙江理工大学经济管理学院，杭州310018)

摘要:鉴于我国普遍存在着信用集中风险和对信用集中风险经济资本测度的研究薄弱性，文章构建了包含信用集中风险的名称、部门和传染三大维度、且与Basel II和III监管要求相一致的信用集中风险经济资本测度的综合模型(CCRM)，并运用CCRM法对我国商业银行典型组合的信用集中风险经济资本进行了仿真研究。结果表明：该典型组合存在着显著的信用集中风险；相比较于HHI指数法、Monte-Carlo模拟法和ASRF调整模型法，CCRM法具有计算耗时少、结果稳健的优点，其较好地测度了我国商业银行中存在的信用集中风险程度。因此，CCRM模型改进了传统商业银行实践中所采用的HHI指数法和Monte-Carlo模拟法等，将在我国信用集中风险经济资本测度中发挥重要作用。

关键词：信用集中风险；经济资本；CCRM；商业银行；Basel监管协议

随着Enron、Worldcom等破产，国内外学者们开始关注银行安全和信用集中风险问题，并将信用集中风险视为现代金融的两大新兴研究主题之一[1]。所谓信用集中风险，巴塞尔银行监管委员会(BCBS)对其的界定是：信用风险内部评级法(IRB)所刻画的信贷组合风险与其真实风险之间的差距，其包括名称信用集中风险(name concentration risk)、部门信用集中风险(sector concentration risk)和传染信用集中风险(contagion concentration risk)[2-3]。

概括而言，目前国外学者对信用集中风险的研究主要集中于某一类信用集中风险的测度，而较少有学者对名称、部门和传染这三类信用集中风险构建统一模型[4]。学者们早期运用“无模型”的HHI指数法、“基于模型”的GA法以及基于组合投资思想的测量法[5-6]对名称集中风险进行了研究；随后由于意识到“部门集中风险比名称集中风险具有更大的危害性和测量难度”[1]，从而开始关注产业与区域部门集中风险，运用“比较多因素模型类方法”[3，7]、“简约模型扩展类方法”[8-11](如二项式扩展技术模型、传播模型和分散化因子模型等)对部门集中风险进行了分析；然而，对于传染集中风险的单独研究却较少，其更多地是基于信用传染的框架[12]。因而，“如何根据我国商业银行实际情况构建起包括名称、部门和传染信用集中风险三大维度的分析模型”，是获得精确经济资本计算的前提。

其次，Basel II和III的Pillar 1中采用了VaR(value at risk)法测度经济资本。该方法在ASRF框架下是成立的，然而，一旦偏离ASRF的假设条件，尤其是在非渐进组合和多因素模型中，VaR方法则常常会因为不满足“次可加性”等内在一致性要求而受到攻击[13]；而相反，ES(expected shortfall)方法则不存在这些问题。纵观上述信用集中风险的研究文献发现，测度信用集中风险的大多数研究仍采用了VaR方法[7，12，14-15]，因此，就需要采用ES等方法对测度进行改进，从而满足风险测度的一致性要求[16]。

目前，国内对信用集中风险的研究还处于定性分析阶段，如杨继光等[17]、徐少君等[2]、颜新秀等[18]、欧阳正仲[19]、巴曙松等[20]。对信用集中风险的定量研究较少，李红霞[21]用HHI指数法和二项式扩展技术对客户集中度风险和部门集中度分析进行了分析；李芳等[22]对银行信贷集中的风险与收益进行了实证。总体上而言，国内研究较少有对信用集中风险的综合测度进行定量分析，更不用说是与Basel监管要求一致的“信用集中风险模型”的开发。固然，这一方面是由于数据的匮乏导致了定量研究无法进行，而更重要的一方面则是由于缺乏对我国信用集中风险的模型研究。

从实践角度看，目前，我国银行业普遍存在着信用集中风险问题，尤其是信贷大客户及贷款行业过度集中问题，往往衍生出大量信用集中风险。信用集中风险的急剧上升，将使银行更容易受到宏观经济波动和企业经营周期影响，甚至可能出现系统性风险，潜在地影响着我国银行体系的稳定性，所以对我国银行信用集中风险的研究显得十分紧迫。

因此，针对我国商业银行普遍存在的信用集中风险、以及国内对信用集中风险定量研究的稀缺现状，本文构建了包含信用集中风险的名称、部门和传染三大维度、且与Basel II和III监管要求相一致性的我国商业银行信用集中风险经济资本测度的综合模型(credit concentration risk model, CCRM)，并用此模型仿真研究了我国商业银行的信用集中风险、测度了其经济资本值。本研究不仅可以丰富信用集中风险的理论研究内容，深化对信用集中风险的综合刻画，更好地与Basel监管要求相一致；同时，也可以刻画出我国商业银行的真实信用集中风险程度，提高我国商业银行的信用风险管理水平和管理质量。

一、纳入信用集中风险的经济资本测度模型：CCRM

ASRF模型是建立在完美分散化、单一系统性因素和违约条件独立性假设条件下，但这无法描述现实中广泛存在的信用集中风险。为此，本文基于ASRF模型的基本分析框架，借鉴Pykhtin[7]关于多因素调整模型方法，吸收Egloff等[12]关于信用传染的思想，构建起包含名称集中风险、部门集中风险、传染效应的信用集中风险模型。同时，考虑到Bonti[23]提出的“监管一致性”要求，借鉴Gürtler等[16]所采用的置信度调整方法，将VaR调整为ES方法对经济资本进行合理的测度，从而获得Basel II和III框架一致条件下的信用集中风险经济资本测度的综合模型：CCRM。

(一)基础分析框架

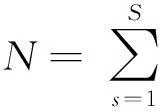
假设当s部门中借款者i的财务状况rsi(潜变量，可理解为资产收益率，其服从标准正态分布，且线性依赖于部门系统风险因素和传染因素)小于违约阈值γsi时触发i违约，即借款者i的无条件违约概率PDsi为：PDsi=P(rsi≤γsi)，进一步可得：

(1)

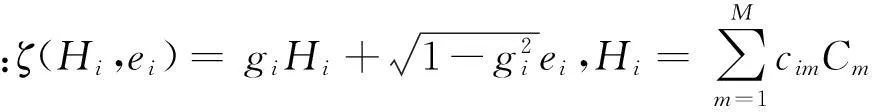
进一步假设s部门中借款者i的LGDs i为一随机变量，其均值为ELGDs i，标准差为VLGDs i，且各LGDs i之间、LGDs i与其他变量间均满足相互独立的条件。于是，可得到组合损失率L：

(2)其中:Φ-1(·)为累积正态分布函数的逆函数，Ι{·}为指示函数，当满足rs i≤Φ-1(PDs i)时取1，否则取0。

若组合足够大且可被视为完美分散时，异质风险消失、只剩下系统风险和传染效应，此时，式(2)的极端损失分布可表示为：

(3)

(二)未经置信度调整的模型

借鉴Pykhtin[7]等思想，下文将提出构建包含三维度(名称、部门、传染)信用集中风险的解析方法，用ES法来测量信用集中风险下的经济资本值。

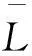
(4)

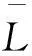
于是，式(1)在ASRF调整模型(下文称ASRF*模型)中，则变为：

(5)

(6)

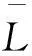
此时，在考虑三大风险后，式(1)可转化为：

(7)

运用泰勒展开式，可得到考虑三大类集中风险后的组合损失的qth分位值(即VaR)为[24]：

(8)

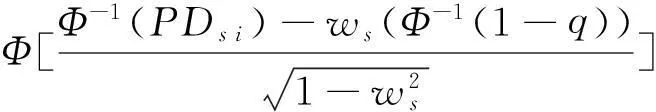
此时，包含三维度风险的经济资本ECCCRM为：

(9)

对应的ASRF*模型的经济资本EC*则为：

(10)

其中:预期损失EL为(置信度q=99.9%)，

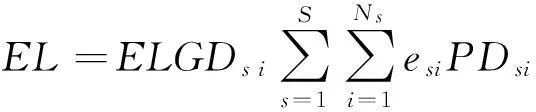
虽然VaR法在实践中有一定应用，但其无法满足风险测度一致性要求，因此，拟采用Acerbi和Tasche[25]提出的ES法进行计算。与VaR计算程序类似，即有：

(11)

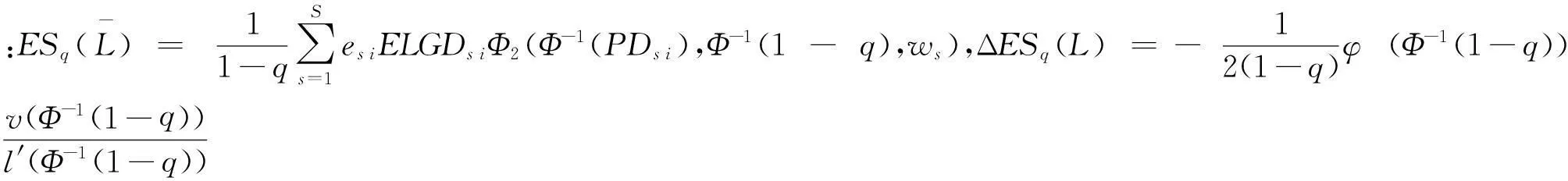
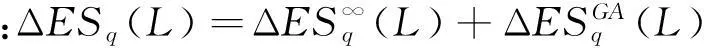
(三)经置信度调整后的CCRM模型

借鉴Gürtler等[16]的“调整置信度”方法，构建Basel框架一致条件下的信用集中风险测度模型。一方面，满足Pillar2所提出的“要充分考虑信用集中风险的要求”，用ES法构建信用集中风险模型；另一方面，也必须符合在Pillar1下的ASRF框架下“用VaR法和ES法得到的资本要求是一致的”这一条件。因此，考虑在ASRF框架中与置信度为q=99.9%的组合VaR值一致的ES值，设需设置的ES置信度为z*，其需满足如下关系：

(12)

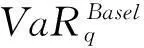
(13)

N2(-N-1(z*),N-1(PDi),βi)

(14)

至此，可根据与VaR99.9%置信度一致的ES计算，得到ES的置信度z*，从而运用CCRM基本模型进行三维度信用集中风险存在条件下的经济资本综合测量。

二、基于信用集中风险的经济资本仿真测度

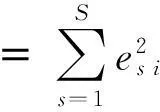
(一)“基准组合”的分析

由于数据可获性限制，选取了典型组合进行仿真分析，见表1。其中“基准组合”表示我国银行系统中典型存在的部门累积敞口分布情况。假设组合中的各敞口同质，组合总规模为6000000元，由6000个相同规模的信贷业务组成。根据Basel中IRB模型设定的监管要求，每一借款者i的违约概率PDs i为2%，ELGDs i为45%、VLGDs i为20%，且设“基准组合”中部门因素的依赖权重系数βis对于所有的部门s均为0.50，传染系统因素设仅有一个，其负载权重系数为0.2。

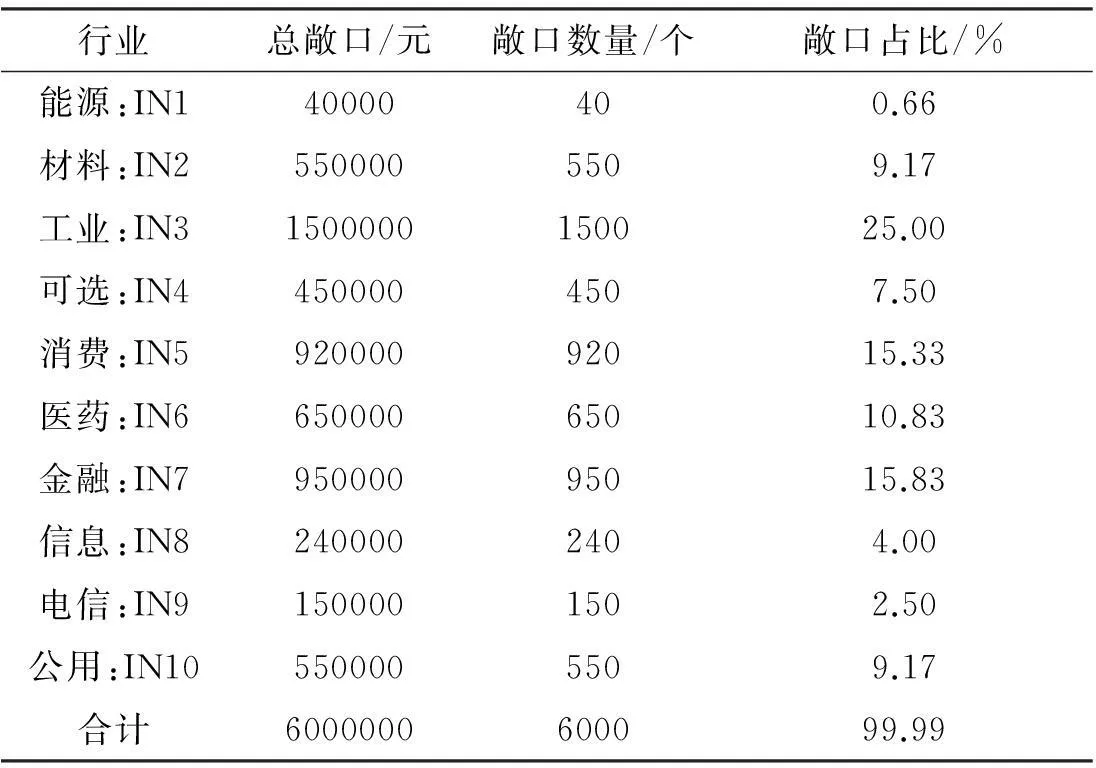
表1　“基准组合”的信贷敞口组成情况

注：“基准组合”的部门划分按照沪深300指数的行业分类进行。

考虑到与Basel 监管相一致的要求(VaR的置信度是99%)，ES的置信度调整为z*=99.68%。运用HHI指数法、Monte-Carlo模拟法、ASRF*模型法和CCRM法分别对“基准组合”进行分析，上述四种方法的计算结果如表2所示。

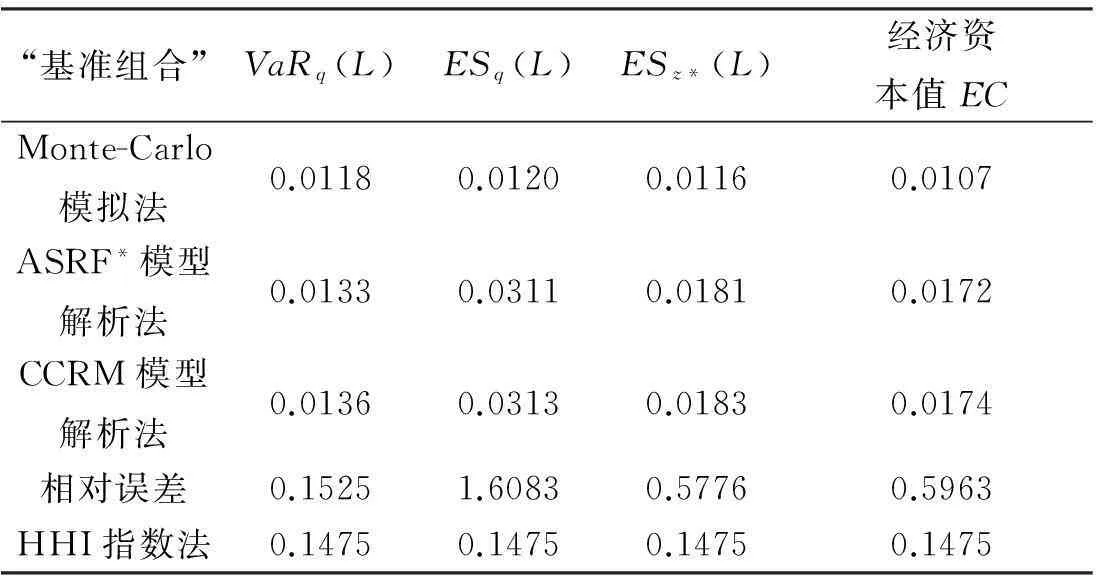
表2　 4种方法下“基准组合”的经济资本

注：VaR置信度为99%，ES置信度调整为99.68%。相对误差=(CCRM模型解析法对应值-Monte-Carlo模拟法对应值)/ Monte-Carlo模拟法值。经济资本EC=ESz*(L)-EL，而EL=0.009。Monte-Carlo模拟法采用10000次模拟量，以获得稳健模拟结果。表中数值表示占组合总敞口的%。下文同。

由表2可知，CCRM模型下得到的无论是VaRq(L)值还是ESz*(L)值，均大于Monte-Carlo模拟法下的结果，对应地，CCRM法下经济资本值要远远大于Monte-Carlo模拟法下的经济资本，其相对误差达到了60%。这表明，目前我国银行所采用的模拟法在一定程度上低估了信贷组合的真实风险值，导致了经济资本准备不充分。

同时，表2也显示，用CCRM法计算ESq(L)和ESz*(L)的相对误差分别为161%和58%，这从另一个角度说明了“为保持Basel监管框架的一致性，必须进行置信度调整”。

与ASRF*模型法相比，CCRM法下得到的风险值略大，其差值分别为：Δtq=0.0003(VaRq)、ΔESq=0.0002(ESq)、ΔESz*=0.0002(ESz*)。这表明，分散化调整效应GA和多系统因素效应∞增加了信贷组合的整体风险，显示出信贷组合中“集中风险”而非“分散风险”的作用。

此外，HHI指数法得到的集中度指数明显与其余三种方法下的信用集中度衡量结果有很大差异，这显示出HHI指数法由于未考虑信贷组合特征而带来的测度差异。

(二)稳健性检验

上述“基准组合”反应了真实世界中广泛存在的信用集中风险，为进一步研究参数设置对信用集中风险测量的影响，本部分内容将在“基准组合”基础上，适当改变参数设置，从而检验CCRM法的稳健性。

1.βis和PDsi变化的影响

对于βis，“基准组合”采用了Basel II监管资本所推荐的简单设置方法，实际上，对于不同借款者i所具有的不同PDsi值，Basel II建议也可根据无条件违约概率PDsi和βis间的关系式、运用历史数据获得，结果如表3所示。

表3　“组合1”各行业部门的违约率PDsi和对应的βis

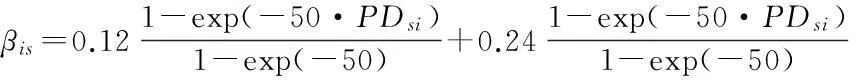
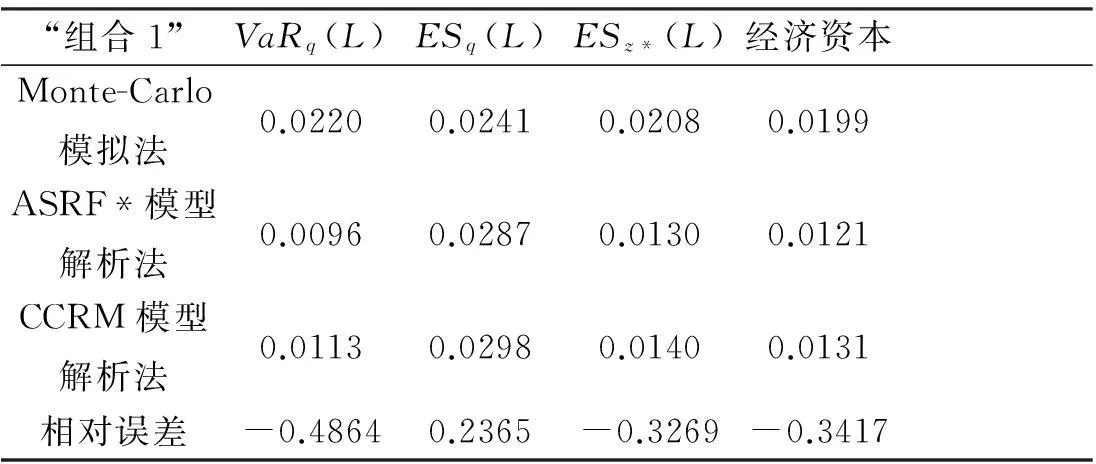
表4　“组合1”的经济资本计算结果

注：VaR的置信度为99.9%，ES的置信度调整为z*=99.52%。

尽管三种方法测量风险的相对误差较大，但一旦与“基准组合”进行比较，就可发现，实际上，ASRF*模型和CCRM的解析解保持了相对稳定性，而Monte-Carlo模拟法下却显著地提高了对风险值的估计，如图1所示。所以，该结论提供了一个警示：模拟法只有在模拟次数“足够多”的情况下才能显示稳健结果，否则可能会导致结果出现一定的偏差。但该“足够多”条件对计算时间要求过高，实践中不可能“足够多”地运行模拟程序。相反，ASRF*模型法和CCRM法还是较好地支持了“解析解稳健性”这一结论。因而，在实践中，宜采用CCRM法等解析方法来获得信用集中风险经济资本测度的稳定结果。

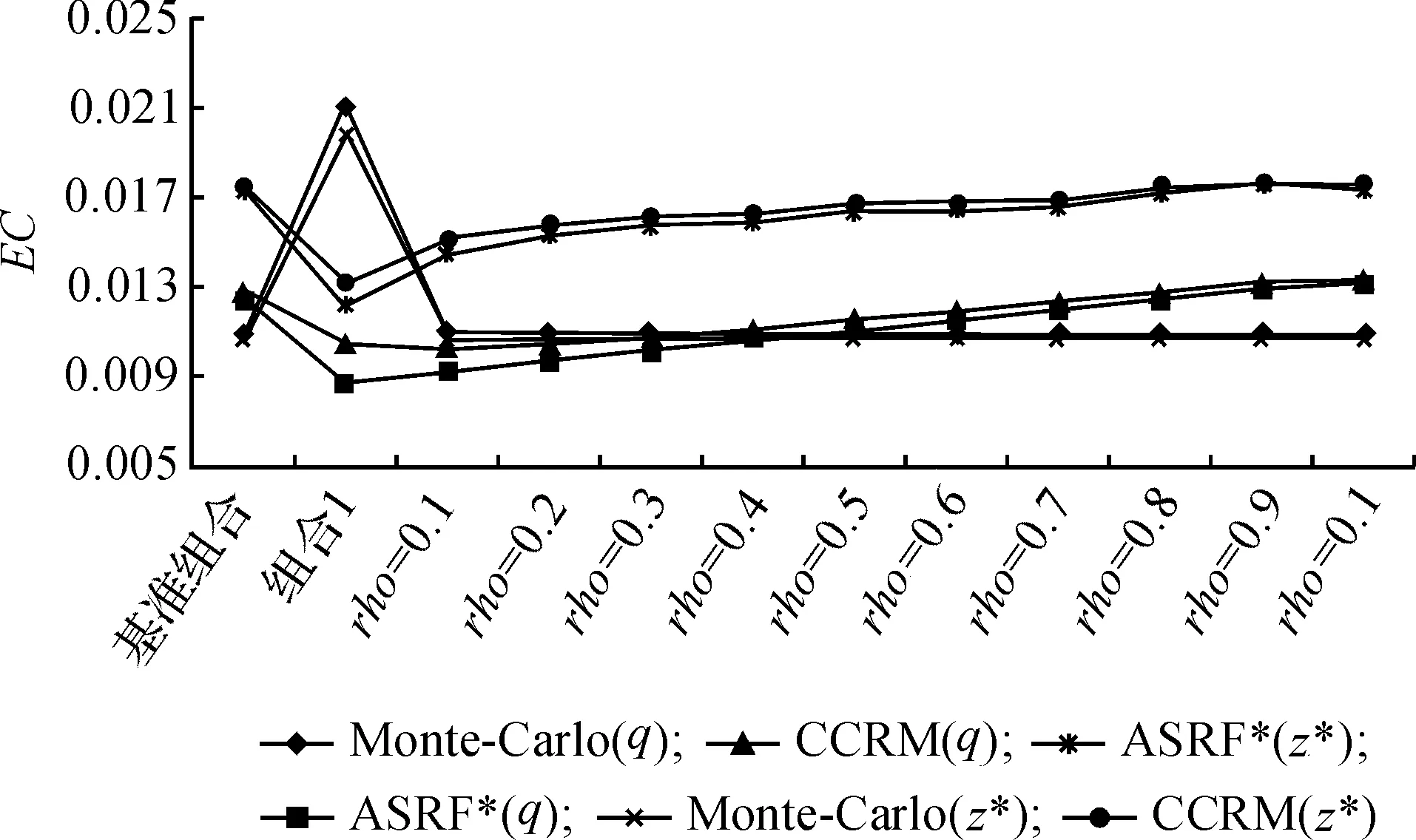
图1　基准组合、组合1和组合2的经济资本比较

2.ρ0变化的影响

上文“基准组合”中，产业间相关系数ρ0是由实际产业股指收益的相关性计算而来。为考虑ρ0对经济资本测度的影响，将ρ0同质化处理，假设不同产业部门之间的相关系数均相同，分别设置为：0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1，此为“组合2”。 由于运用Monte-Carlo模拟方法得到的结果与“基准组合”一致。因此，对这10个ρ0运用类似的计算方法进行ASRF*模型法与CCRM法的比较，结果如表5所示。

从表5可以看出，随着ρ0ij从0.1增加至1.0，其对应地风险值均不断增加，呈现出单调递增的关系；然而其变动范围均比较平稳，所对应地均值与“基准组合”保持了相对较高的一致性，如图1所示。因而，ρ0ij参数的变化从整体上而言并不会显著影响“组合2”的风险值，也就是说，“基准组合”中的ρ0采用实际产业间相关性数值，具有较好的稳健性。

与“基准组合”类似，“组合2”中CCRM法下的风险值大于ASRF*模型法下的风险值。该结果再一次显示：分散化调整效应GA和多系统因素效应∞对“集中风险”而非“分散风险”的正向作用。

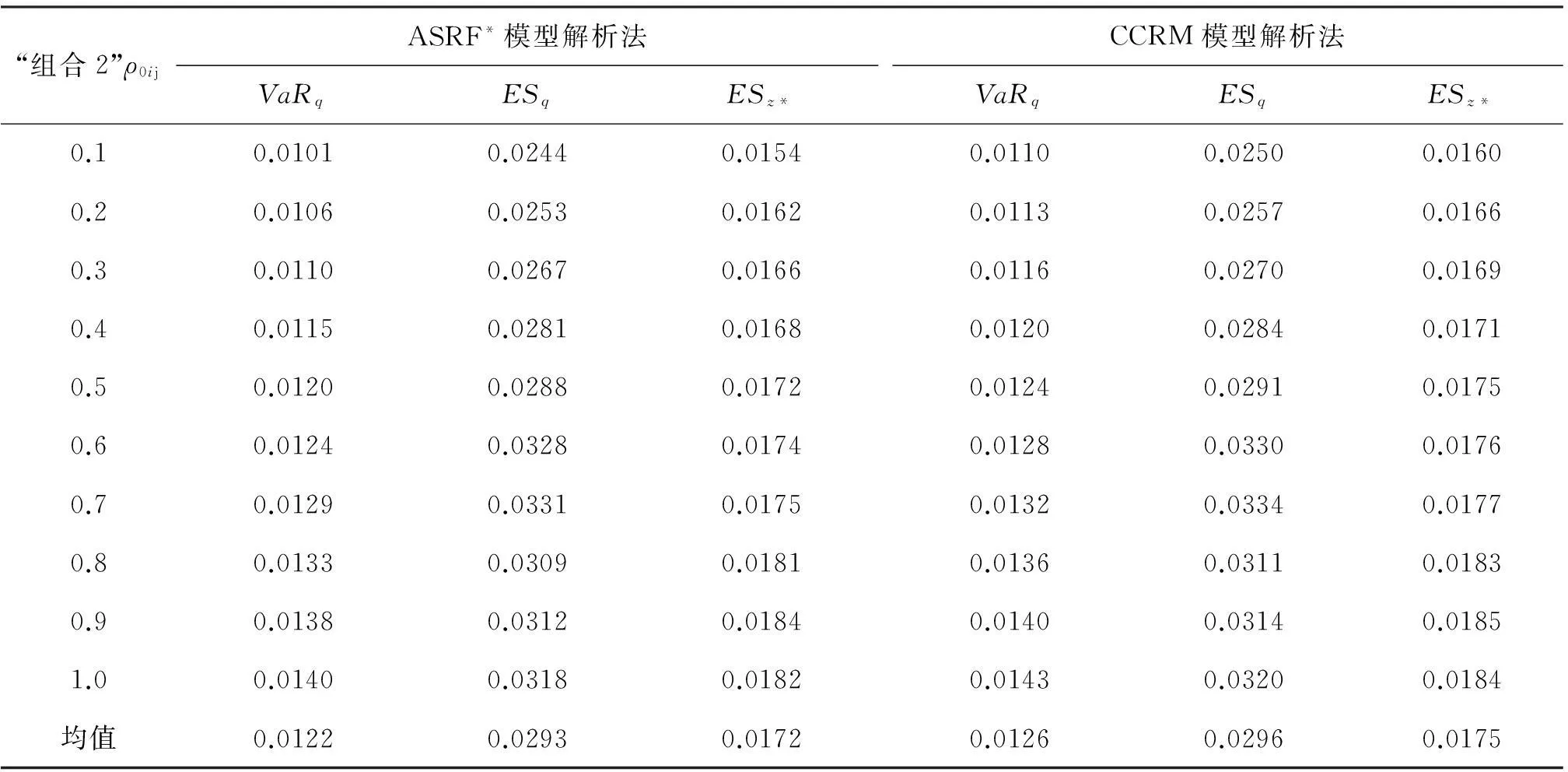
表5　“组合2”的经济资本计算结果

注：VaR的置信度为99.9%，而ES的调整置信度为99.68%。ρ0ij表示i产业与j产业间的相关系数。

综上所述，调整各部门行业的违约率PDsi和对应的βis(“组合1”)、以及产业间相关系数ρ0(“组合2”)等参数，用CCRM法计算信贷组合的经济资本值仍与“基准组合”的经济资本值类似，从而显示出CCRM解析法求解经济资本值具有的良好稳健性；而且凭借着该解析法计算耗时较少等优点，其将在实践中将有一定的应用前景。

三、结论

本文基于现有信用集中风险研究文献存在的“较少对名称、部门、传染三大维度信用风险进行综合研究”、“较少考虑与Basel监管要求相一致”这两个问题，构建了与Basel II和III监管要求相一致的信用集中风险经济资本测度的综合模型：CCRM。因此，该模型的构建具有理论上的合理性，相对完整地构建了信用集中风险的框架、较好地实现了测度的一致性原则。

从实践角度而言，由于缺乏银行具体的全部信贷数据而无法检验我国商业银行真实的信用集中风险程度，基于此，选取了我国商业银行信贷的典型组合，运用CCRM方法对该组合的信用集中风险程度进行了仿真测度，并与实践中使用的传统HHI指数法和Monte-Carlo模拟法、以及Basel监管协议下的ASRF*模型法进行了对比研究。仿真结果表明：a)用CCRM法计算信贷组合的经济资本具有较强的稳健性，并且所得到的经济资本值往往高于ASRF*模型解析法下的经济资本值，也就是说，分散化调整效应GA和多系统因素效应∞增加了信贷组合的整体风险，证实了我国信贷组合中存在着“集中风险”而非“分散风险”；b)CCRM法凭借着其在求解经济资本值具有良好的稳健性和计算耗时较少等优点，在实践中将优于Monte-Carlo模拟法；c)传统采用的HHI法既无法反映出信贷组合的质量，也与CCRM等方法测量的真实经济资本值相差甚远，因此，在实践中不宜采用HHI指标法；d)用传统的VaR法计算经济资本将会导致对我国信贷组合所需真实经济资本的严重低估，而CCRM法采用置信度调整的ES策略对信用集中风险经济资本进行测度具有良好的稳健性。因此，CCRM模型相比较于HHI指数法、Monte-Carlo模拟法和ASRF*模型法，其具有计算耗时少、结果稳健等优点，体现出一定的实践应用合理性，将在我国信用集中风险的衡量及经济资本的计算中发挥重要的作用。

参考文献：

[1] LUCCHETTA M. Does the bank risk concentration freeze the interbank system[J]. The North American Journal of Economics and Finance, 2015, 17(1): 1-18.

[2] 徐少君，金雪军．信用集中风险研究新进展[J]．金融理论与实践，2010(7)：3-8．

[3] DUETTMANN K. Measuring concentration risk in credit portfolio[J]. The Analytics of Risk Model Validation, 2008(5): 59-78.

[4] GORDY M. A risk-factor model foundation for ratings-based bank capital rules[J]. Journal of Financial Intermediation, 2003, 12(3): 199-232.

[5] UBERTI P, FIGINI S. How to measure single-name credit risk concentrations[J]. European Journal of Operational Research, 2010, 202(1): 232-238.

[6] RAO P, YUE H, ZHU J. An investigation of credit borrower concentration[J]. Journal of Banking & Finance, 2015, 54(2): 208-221.

[7] PYKHTIN M. Multi-factor adjustment[J]. Risk, 2004(3): 85-90.

[8] SEMPER J, BELTRAN J. Sector concentration risk: a model for estimating capital requirements[J]. Mathematical and Computer Modelling, 2011, 54(7): 1765-1772.

[9] CHEN Y, WEI X, ZHANG L. A new measurement of sectoral concentration of credit portfolio[J]. Procedia Computer Science, 2013(17): 1231-1240.

[10] GORDY M, MARRONE J. Granularity adjustment for mark-to-market credit risk models[J]. Journal of Banking & Finance, 2012, 36(7): 1896-1910.

[11] CESPEDES G J C, DE JUNA HERRERO, KEININ A, et al. A simple multi-factor factor adjustment for the treatment of diversification in credit capital rules[J]. Journal of Credit Risk, 2006, 2(3): 57-85.

[12] EGLOFF D, LEIPPOLD M, VANINI P. A simple model of credit contagion[J]. Journal of Banking & Finance, 2007, 31(8): 2475-2492.

[13] ARTZNER P, DELBAE F, EBER J M, et al. Coherent risk measures[J]. Mathematical Finance, 1999, 9(3): 203-228.

[14] HEITFIELD S, BURTON E, CHOMSISENGPHET S. Systematic and idiosyncratic risk in syndicated loan portfolios[J]. Journal of Credit Risk, 2006, 2(3): 3-31.

[15] DÜLLMAN K, MASSCHELEIN N. A tractable model to measure sector concentration risk in credit portfolios[J]. Journal of Financial Services Research, 2007, 32(1): 55-79.

[16] GÜRTLER M, HIBBELN M, VOHRINGER C. Measuring concentration risk for regulatory purposes[J]. Journal of Risk, 2010, 12(3): 69-104.

[17] 杨继光，刘海龙．商业银行组合信用风险经济资本测度方法研究[J]．金融研究，2009(4)：143-158．

[18] 颜新秀，王睿．银行业集中度风险的计量与监管:国际经验及对我国的启示[J]．中国金融，2010(3)：23-25．

[19] 欧阳正仲．信用集中度风险与经济资本研究[J]．金融与经济，2012(7)：76-78．

[20] 巴曙松，陈剑．贷款集中度风险：当前信贷风险管理与监管的关键因素[J]．金融管理与研究，2010(8)：8-21．

[21] 李红霞．商业银行贷款款集中度风险的计量与实证研究[J]．海南金融，2010(2)：25-30．

[22] 李芳，陈德棉．中国银行业信贷集中的风险收益效应分析[J]．财贸研究，2011(1)：94-98．

[23] BONTI G, KALKBRENER M, LOTZ C, et al. Credit risk concentrations under stress[J]. Journal of Credit Risk, 2006, 2(3): 115-136.

[24] MARTIN R, WILDE T. Unsystematic credit risk[J]. Risk Magazine, 2002, 15(11): 123-128.

[25] GOURIEROUX C, LAURENT J P, SCAILLET O. Sensitivity analysis of values at risk[J]. Journal of Empirical Finance, 2000, 7(3-4): 225-245.

[26] ACERBI C, TASCHE D. On the coherence of expected shortfall[J]. Journal of Banking and Finance, 2002, 26(7): 1487-1503.

(责任编辑： 陈和榜)

DOI:10.3969/j.issn.1673-3851.2016.02.004

收稿日期：2015-05-04

基金项目：国家自然科学基金项目(71103161)；浙江省高校人文社科重点研究基地(浙江理工大学应用经济学)项目(2014YJZD07，2014JDLXZD06)；浙江理工大学521人才培养计划

作者简介：徐少君(1979-)，女，浙江宁波人，副教授，博士，主要从事金融风险管理等方面的研究。

中图分类号：F832

文献标志码：A

文章编号：1673- 3851 (2016) 01- 0020- 08 引用页码： 020104

Research on Credit Concentration Risk and Its Economic Capital Measurement of Chinese Commercial Banks

XUShaojun

(School of Economics and Management, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Abstract：In view of the widespread credit concentration risk in China and the weak economic capital measurement of credit concentration risk, this paper constructs an integrated model to measure the economic capital of credit concentration risk (CCRM) which is consistent with the Basel II & III regulatory requirements and contains three dimensions of credit concentration risk: name concentration risk, sector concentration risk and contagion risk. Then, this paper carries out the simulation study on credit concentration risk and economic capital in Chinese commercial banks with CCRM method, and finds that there are significant credit concentration risk. Besides, CCRM method is better than HHI index, Monte-Carlo simulation and the ASRF* model with less time-consuming calculation and more robust results in Chinese credit portfolios. Hence, CCRM model well measures credit concentration risk degree in Chinese commercial banks and will play an important role in measuring the economic capital of credit concentration risk in Chinese commercial banks.

Key words：credit concentration risk; economic capital; CCRM; commercial bank; basel regulation agreement