一个改进的就地稳定二路归并算法

胡圣荣,杨文君

(1.华南农业大学 工程基础教学与训练中心，广东 广州 510642；2.怀雅逊大学 电子与计算机工程系，安大略 多伦多 M5B 2K3)



一个改进的就地稳定二路归并算法

胡圣荣1,杨文君2

(1.华南农业大学 工程基础教学与训练中心，广东 广州 510642；2.怀雅逊大学 电子与计算机工程系，安大略 多伦多 M5B 2K3)

摘要：提出溢出队列的概念，用于管理二路归并过程中的动态存储区，它位于第二归并段的头部，存放归并时前段的较大者；对一个二路归并算法进行了改进，将理顺队列改为理顺溢出队列，并保留了原算法简便、就地进行、稳定、比较次数最优的特点；进行了二路归并和二路归并排序测试，结果表明归并总长为n的两个等长归并段时移动次数约为n2/108，可减少到原算法的4/9。

关键词：归并；就地归并；归并排序；溢出队列

在计算机相关学科中，有序区的归并算法有重要意义，如用于排序问题的二路归并排序。但经典的归并算法需要O(n)的辅助空间。

为此很多文献研究附加空间少的甚至就地归并的算法，其中采用了一些特殊的技术或技巧，如“内部缓存”技术[1]、邻块交换的旋转算法[1]、连续交换中的浮洞技术[1]等。不难发现，很多算法过于追求“就地”与“线性性能”，结果比较复杂，而线性因子也可能较大；还有些放弃了稳定性。Geffert等的稳定算法比较典型，最多m(t+1)+n/2t+o(m)次比较，5n+12m+o(m)次移动[1]，其中m≤n，t=[log2(n/m)]。这类算法中Kim的实现[2]有一定实用性，但仍很复杂。若放松严格的“就地”要求，允许O(log2n)的附加栈空间，如Ellis和Markov的ShuffleMerge算法[3]，虽不是线性的，但简洁实用。Dalkilic的实现[4]则进一步提高了时空性能和实用性。

本文对一个就地归并算法进行了改进，保持了原算法简便、稳定、就地进行、比较次数最优的特点，但移动次数可减少一半以上。

1算法

设二路归并的初始归并段为A[i, j)、B[j, to)(它们存放于同一数组R中)。

算法Ⅰ[8]：对A、B段从前向后扫描，设当前位置分别为i、p；在[j, p)之间形成动态存储区，存储归并时A段大于B[p]者(它们后移而成，其值大于A段已归并好的部分)，并组织成循环队列。于是：

(1)若队头≤B[p]，则队头出队(前移到A[i]位置)，原A[i]入队(后移到原队头位置)，队头位置循环后移1位；

(2)若队头>B[p]，先理顺队列(队头开始的后段与前段交换，使队头位于缓冲区开始位置)，然后将B[p]前移到A[i]位置，原A[i]入队(后移到B[p])，队列长度增1，但队头位置不变。

以上方法在情况(2)时，入队后队列长度增1，由于是顺序存储，入队前进行了队列理顺操作(使入队后队列元素大小排列正常)，这在多次入队时会导致队列元素的多次反复移动。显然若减少队列的理顺操作，就可减少移动量。

算法Ⅱ：修改算法Ⅰ，当情况(2)队头>B[p]时，前部的A[i]入队时仍存放到B[p]位置，但并不理顺队列，这时缓冲区中在循环队列后又形成一个存储区，不妨称“溢出区”或“溢出队列”。这时当情况(1)队头≤B[p]，队头出队时需要理顺队列，易见这只需理顺溢出队列即可：将它与循环队列中队头开始的后段交换。交换后溢出区合并到了循环队列中，循环队列长度增加，(当前)溢出区消失。

比较两种理顺操作，一种在入队时进行，一种在出队时进行；假设出、入队概率相当，则因归并过程中循环队列可能较长，队头之前的部分(平均)也就较长，而溢出队列会相对短些，故理顺溢出队列的移动量会小些。后面的测试结果验证了这种定性分析(大规模时可减少一半以上)。

与算法Ⅰ类似，归并过程中可能出现两种情况：

(1)若原B段已处理完，则理顺队列，归并结束。

(2)若原A段已处理完，则理顺队列作为新的A段，与p开始的B段继续归并。

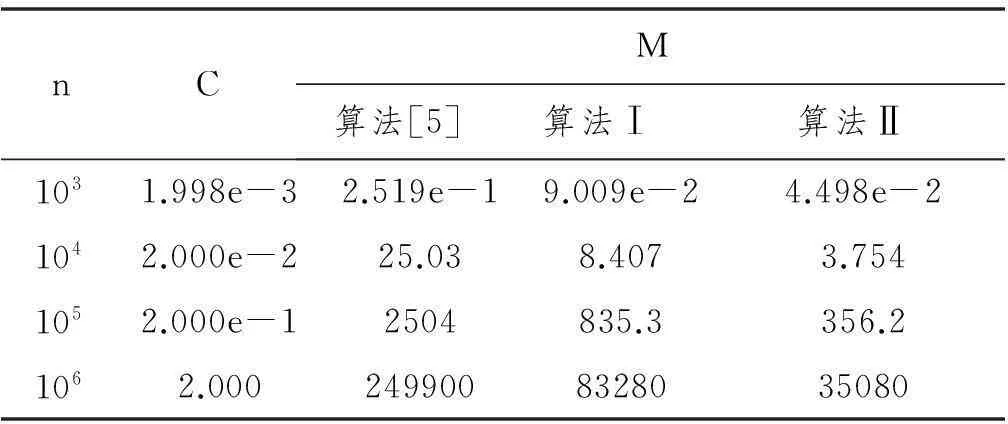
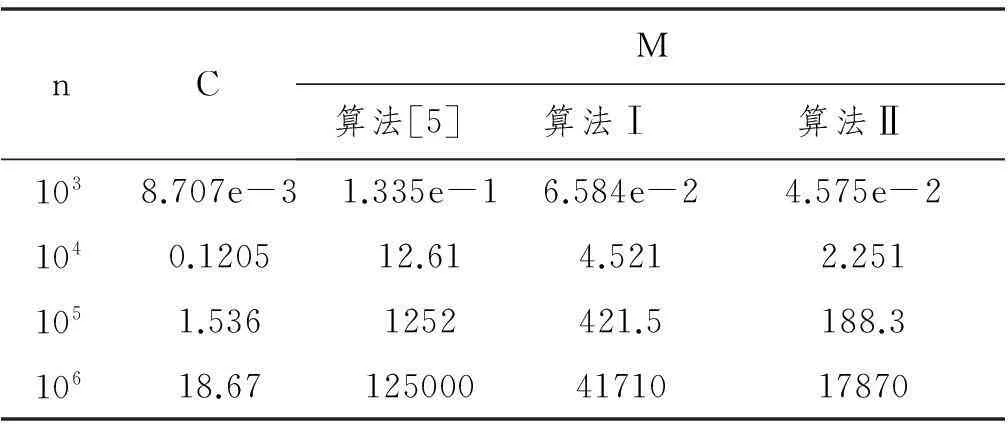
参见图1，设循环队列、溢出队列长度分别为n、m，归并算法如下：

L1：while(i

L2：if(i>=j) 结束返回;

L3：交换R[i]和R[j];f=0,n=1,m=0;//初始队列i++,p=j+1;

L4：while(i

if(队头<=R[p]) {

if(m>0) {理顺溢出队列;f=f+m;n=p-j;m=0;}

队头出队并置于R[i]，原R[i]入队，i++;}

else {

交换R[i]和R[p];

if(f==0) n++; else m++;

i++;p++;}

L5：if(p>=to) {

理顺队列;交换R[i,j)和R[j,p);结束返回;}

else {理顺队列;i=j;j=p;转L1;}

其中理顺溢出队列是交换R[j+f, p-m)和R[p-m, p)，理顺队列是交换R[j, j+f)和R[j+f, p-m)，它们是相邻块交换，可用旋转算法[1]实现，它交换长度为m、n的相邻两块移动量为m+n+GCP(m,n)，其中GCP为求最大公约数。

图1采用溢出队列的二路归并

以上两个算法，每比较一次就有一个元素到位，故若归并长度分别为m、n的两个有序段，比较次数最多m+n-1次。如果队列中不出现理顺操作，则A段元素最多入队、出队1次，加上B段元素的移动，移动量最好O(m+n)；但一般要多次理顺队列，移动量最坏O(mn)。两个算法都是稳定的。

2性能分析与测试

这里进行了两种测试：(1)归并算法测试，取2个长度都为n的随机序列，分别排序(得到有序序列)后再进行归并，考察归并的比较次数、移动次数等[2-5]，结果见表1。(2)归并排序测试，将归并算法用于归并排序，通过排序的比较次数、移动次数间接考察归并的比较次数、移动次数，结果见表2。表1、表2中C、M表示关键字比较次数(106)、移动次数(106)；三个算法的比较次数相同。

测试时随机序列的生成采用文[6]的长周期随机函数，各规模下测试若干组后对结果平均。各组随机序列是在长周期随机序列中依次截取(不改变种子)。组数的多少自动调整：最多106组，以该规模总排序时间不超过1分钟为准，但最少10组。算法[5]改自文[5](原文可能排印瑕疵，比较次数有多余)。

表1　归并测试结果(/106)

表2　归并排序测试结果(/106)

采用更多测试数据(略)，对表1、表2进行类似文[7]的稳定性拟合，结果为：

对表1，算法[5]、算法Ⅰ、算法Ⅱ归并的比较次数约为2n，移动次数分别约为n2/4+1.85n、n2/12+6.6n、n2/27+7.8n。若n表示归并后的总长度(两段分别长n/2)则相应拟合结果分别为n、n2/16+0.92n、n2/48+3.3n、n2/108+3.9n。

对表2，算法[5]、算法Ⅰ、算法Ⅱ归并排序的比较次数约为1.44nln(n)-1.21n，移动次数分别约为n2/8+1.33nln(n)、n2/24+4.8nln(n)、n2/54+5.5nln(n)。

以上拟合结果高次项(主项)稳定些，低次项略差(原始数据中去掉占主导的高次项后剩余部分精度差，波动较大)。易见，拟合结果符合归并和归并排序的复杂性关系[8]：

f(n)=T(n)-2T(n/2)

如对算法Ⅱ，由归并排序移动次数导出的归并移动次数为：

f(n)=T(n)-2T(n/2)

这与单独归并测试的拟合结果是一致的。

由测试数据及其拟合主项可见，当规模足够大后，算法Ⅰ的移动次数约为算法[5]的4/12=1/3，减少了2/3；而改进的算法Ⅱ移动次数约为算法Ⅰ的12/27=4/9，又减少了5/9，即移动次数又可减少一半以上。

3结论

引入溢出队列对归并算法Ⅰ的缓冲区队列进行改进，将理顺队列改为理顺溢出队列，结果表明对减少移动次数是有效的：在保持算法简便、稳定、就地进行、比较次数最优的情况下，当规模足够大后，移动次数约下降到原算法的4/9，减少了一半以上。

参考文献：

[1] Geffert V, Katajainen J, Pasanen T. Asymptotically efficient in-place merging[J]. Theoretical Computer Science, 2000, 237(1): 159-181.

[2] Kim P S, Kutzner A. On optimal and efficient in place merging[M]//SOFSEM 2006: Theory and Practice of Computer Science. Springer Berlin Heidelberg, 2006: 350-359.

[3] Ellis J, Markov M. In situ, stable merging by way of the perfect shuffle[J]. The Computer Journal, 2000, 43(1): 40-53.

[4] Dalkilic M E, Acar E, Tokatli G. A simple shuffle-based stable in-place merge algorithm[J]. Procedia Computer Science, 2011, 3: 1049-1054.

[5] 范时平, 聂永萍, 汪林林. 一种基于数据块交换的快速稳定原地归并算法[J]. 重庆邮电学院学报 (自然科学版), 2004, 16(4): 93-93.

[6] 胡圣荣. 关于排序算法的随机输入序列[J]. 武汉理工大学学报, 2006, 28(9): 105-107.

[7] 胡圣荣. 关于排序效率的数值估计[J]. 广州城市职业学院学报, 2008, 2(1): 61-64.

[8] 胡圣荣. 一个新的就地稳定归并算法[J]. 河池学院学报, 2014, 34(5): 49-52.

(责任编辑夏侯国论)

收稿日期：2016-05-27

作者简介：胡圣荣，男，华南农业大学工程基础教学与训练中心教授，博士。

中图分类号：TP311.12

文献标识码：A

文章编号：1674-0408(2016)02-0001-04

An improved in-place stable 2-way merge algorithm

HU Sheng-rong1，YANG Wen-jun2

(1. Engineering Fundamentals Teaching and Training Centre, South China Agricultural University, Guangzhou 510642，China;2. Department of Electrical and Computer Engineering, Ryerson University, Toronto Ontario M5B 2K3, Canada)

Abstract：The concept of overflow queue is proposed to manage the dynamical storage buffer, which is located in the head part of the second merge segment and formed by larger elements of the first merge segment in the merging process. The corresponding improved algorithm replaces queue reforming with overflow queue reforming, and retains the good characteristics of the original 2-way merge algorithm, it is simple, in-place, stable, and optimal in comparisons. The algorithm was tested through both merge and merge sort, the results showed the amount of key movement or assignment of the improved algorithm in merging two segments of equal length with total length of n is about n2/108, which is 4/9 of the original algorithm.

Key words：merge; in-place merge; merge sort; overflow queue