一种基于启发式算法的货物装载问题的研究
郑炜, 刘文兴, 杨喜兵, 袁绪龙, 王文鹏
(1.西北工业大学 软件与微电子学院, 陕西 西安 710072; 2.西北工业大学 航海学院, 陕西 西安 710072)
一种基于启发式算法的货物装载问题的研究
郑炜1, 刘文兴1, 杨喜兵1, 袁绪龙2, 王文鹏1
(1.西北工业大学 软件与微电子学院, 陕西 西安710072; 2.西北工业大学 航海学院, 陕西 西安710072)
摘要:文章旨在解决多车辆车厢合理、高效装载问题,即给定一批大小不同的货物和一批车厢大小不同的车辆,在满足货物装载约束条件下实现自动化装载。文章首先分析借助计算机实现自动化装载存在的难点,在此基础上提出一种基于平面分割理论的启发式搜索算法,以解决自动化装载问题,并给出算法优化方法以提高算法的效率与实用价值。最后,为了得到满足货物装载约束条件的最优装载方案,文章也提出了结合遗传算法解决货物装载问题的改进思路。
关键词:成本降低;三维货物装载;多车辆;多货物;平面划分;遗传算法;启发式算法
在货物的流通运输环节中,货物装载工作是最费时费力的部分,直接影响着运输部门的运输效率与成本。随着信息技术的不断发展,货物的装载方案完全可以通过计算机模拟来自动生成,并以此指导装载人员的装载活动,以提高货物运输环节的效率并降低成本。
本文试图构建一种能自动生成装载方案的算法,该算法可以将货物合理有效地装入车辆车厢中,并在满足给定车辆车厢与货物约束条件的情况下装完所有的货物。为了验证算法生成的装载方案的可行性,本文利用SharpGL图形包对生成的方案进行了验证,实验结果表明,该算法可以合理、高效地完成自动化装载。
1货物自动化装载问题
1.1货物自动化装载概述
货物自动化装载问题,简言之就是利用计算机自动生成把不同大小、不同形状的一些货物合理地装到车厢中的方案。
货物装载问题不是一类简单的问题,而是由许多不同种类装载问题所组成的装载问题家族。根据不同的目标和不同的约束条件,可以将其细分为不同的分支。货物装载还是一类多目标组合优化问题,其已被证明为NP-HARD问题[1-2],而解决NP完全问题的一般方法就是利用元启发式搜索算法,不断在解空间中搜索最优解,使得到的最终解尽量达到最优解或者接近最优解。
1.2货物自动化装载问题的分类
货物自动化装载是一个三维空间装载问题,有多种分类方法。目前比较流行的分类方法是由德国人Dyckhoff[3]提出的,他根据货物装载所需要车辆车厢的数量,将装载问题划分为以下2类:
1) 多车辆车厢问题:给定一批货物和一定数量的车辆车厢,要求所有的货物都能装入到车辆车厢内,并且尽可能使所需的车辆车厢最少,本文的主要研究工作是解决此类问题,即满足货物的约束条件下,使得所需要的车辆车厢最少。
2) 单车辆车厢问题:给定一批规格不同的货物并且只给定一个车辆车厢,要求将尽量多的货物装载到给定的单个车厢内,使给定的单个车辆车厢的空间利用率达到最大。
Bortfeldt[4]提出了另外一种比较流行的分类方法,其思路是将装载问题分为3类,即同类问题、弱异类问题、强异类问题。划分依据是货物规格差异的程度:当待装货物规格完全一样时,为同类问题;当待装货物只有少数几种不同规格时,为弱异类问题;当待装货物有很多不同类型时,为强异类问题。
另外,在工程领域中,还可以根据货物约束条件进行分类。例如考虑是否多目的地运送。
1.3货物自动化装载问题的技术难点
通常在解决货物自动装载过程中,存在以下技术难点:
1) NP-HARD问题本身就是一个比较难以解决的技术问题,通常是通过元启发式算法求其比较理想的解,最优解很难通过自动化求解得到。
2) 传统的货物自动化装载大都规定货物的形状为长方体,但是在实际运输过程中,运输的货物很可能是一种不规则形状的货物,或者是一种规则的形状,但不是规则的长方体。在货物形状很多并且车厢尺寸不确定的情况下,解决货物的装载,并且满足装载约束条件是一个技术难点。
3) 在实际摆放时,货物存在着不同的摆放状态,货物的形状即使是长方体情况下,如图1所示,仍可以有6种不同装载状态。
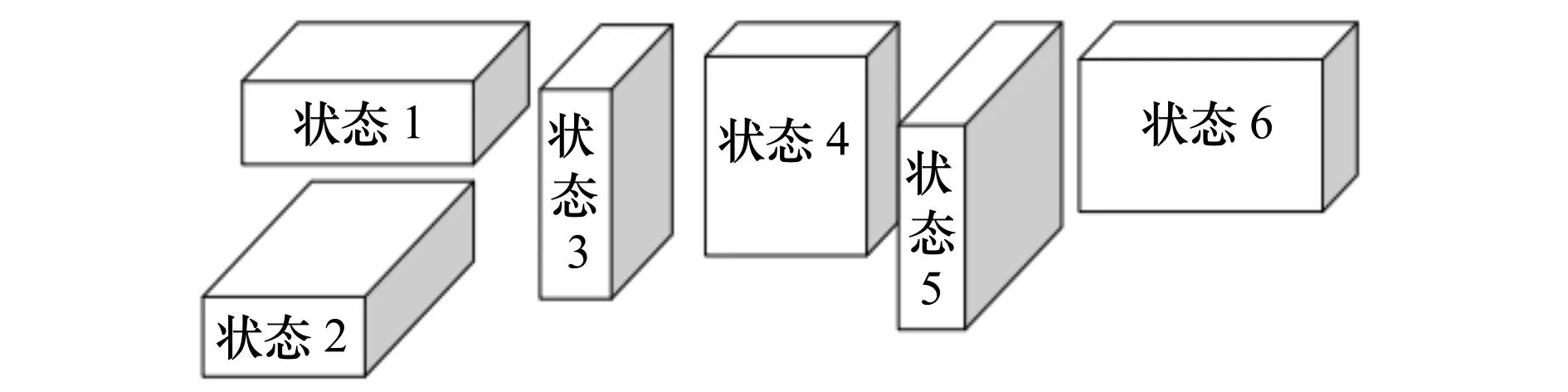
图1 长方体货物的6种摆放状态
4) 所设定的装载约束条件使装载过程变得更为复杂,如Bischoff和Ratchliff[5]总结的货物承重约束、分类约束、稳定性约束、卸载顺序约束、方位约束等。
2一般求解方法
货物自动化装载问题的解决方法目前主要有启发式搜索算法、数学规划法、组合算法[6]。在一般求解货物装载问题用到的启发式算法中,遗传算法是最为广泛使用的一种元启发式搜索算法,属于全局性的搜索算法,能自适应地控制搜索过程,以求得最优解[7]。在解决类似于货物装载这样的NP问题中表现非常卓越,但是其算法时间复杂度很大,并且,搜索结果具有不确定性,使其在实际工程应用中有一定的局限性。
3核心算法
3.1算法基本思想
本文在货物装载约束条件下,探索基于平面划分理论求解货物自动化装载问题,如图2所示。根据货物装载的误差要求以及时间成本要求将车厢内底面划分为不同数量的等面积小格子,这里为了显示方便,将车厢内底面划分为5*4=20个等面积小格子。如要提高装载的精度,可以划分为更多的小格子。
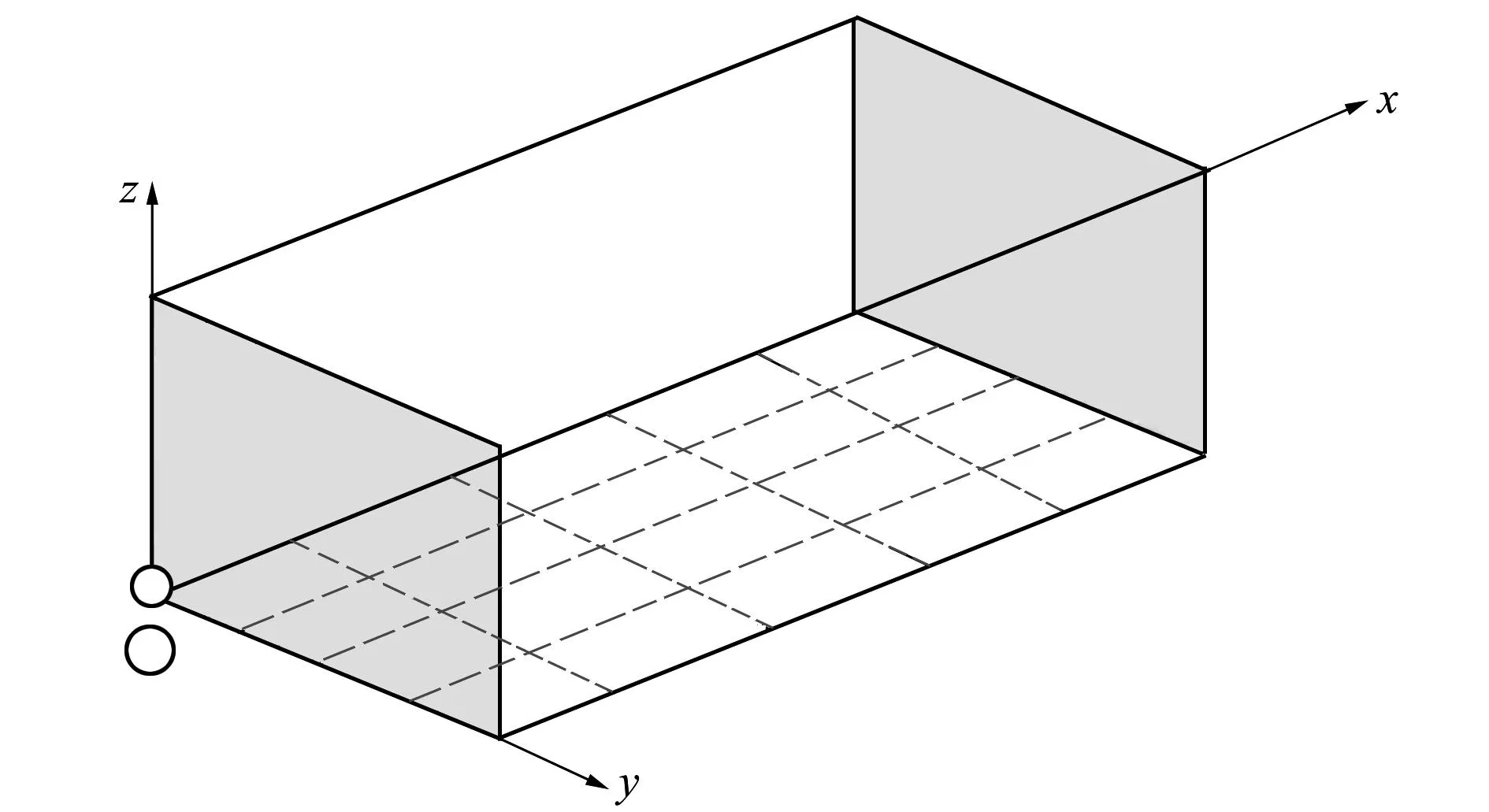
图2 车厢底面分割图
假设货物的装载层数要求为NumLayer,并且货物总是底面接地时,即货物只有如图1所示的第一种和第二种放置状态。当NumLayer为1时,这里优先选择图1的第二种放置状态(在具体的算法实验中,可以优先选择不同的货物放置状态)。利用搜索算法选择一个货物,记当前选择的货物长为Li,宽为Wi,高为Hi,从车厢内底面原点出发,开始顺着X轴正方向依次查找,直到找到第一个空白小格子,开始依次累加小格子的长,当到达车厢内底面边缘或小格子已经填上货物编号,则停止累加。记小格子的累加长为Lsum,当Lsum≥Wi,从找到的第一个空白小格子位置开始顺着Y轴正方向依次累加小格子的宽,当到达车厢内底面边缘或小格子已经填上货物编号,则停止累加。记小格子的累加宽为Wsum,当Wsum≥Li,判断车厢的高是否大于等于货物的高,如大于等于,则将以小格子向X轴正方向累加长为宽与小格子向Y轴正方向累加宽为长的长方形区域填写上货物的编号与货物的摆放状态(图1中状态2),表明当前货物已经装载到车辆车厢中。在累加过程中,如不能同时满足Lsum≥Wi,Wsum≥Li条件,则变换到如图1所示的第一种货物放置的状态,重复操作,若满足Lsum≥Li,Wsum≥Wi,并且货物高小于等于车厢的高时,则将以小格子向X轴正方向累加长为长与小格子向Y轴正方向累加宽为宽的长方形区域填写上货物的编号与货物的摆放状态(图1中状态1),表明当前货物已经装载到车厢中。当以找到的第一个空白小格子为起点顺着X轴与Y轴正方向累加不能搜索到上述长方形区域时,则应顺着X轴正方向与Y轴正方向寻找下一个空白小格子。
当NumLayer≥2时,可以在第二层或者第二层以上建立如图2所示长方形底面,称其为虚平面,并且按照第一层划分小格子的方法划分第二层及第二层以上建立的虚平面,并为货物查找放置区域。在第二层及第二层以上放置货物不同于第一层的是:要累加其下面几层已装载货物的总高度并要判断下层已填长方形区域是否满足叠放条件。
当NumLayer为1时,对上述算法步骤用图像化的方式给出说明。如图3所示。
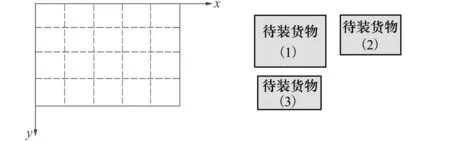
图3 货物装载初始状态
假设车厢底面内长为5 m,内宽为4 m,要求精度为1 m,则可以将车厢内底面划分为5*4=20个小格子。每个格子的长与宽都为1 m。图3右边是待装货物俯视图。将货物编号为1~3。货物1的长度和宽度设为4 m和2 m,货物2的长度和宽度设为3.5 m和1.5 m,货物3的长度和宽度设为2.3 m和1 m。
开始选择编号为1的货物进行装载,从车厢内底面原点开始顺着X轴正方向开始寻找空白小格子,由于第一个为空格子,所以可以从这个位置向X轴正方向进行累加,累加到第二个格子时,累加长已经大于货物1的宽度,然后顺着初始找到的第一个空格子向Y轴正方向累加,到车厢内底面边缘时,车厢内底面宽度恰好等于货物长度,再比较货物1
高度与车厢内高,得出货物高度小于车厢内高,因此将货物1的编号及放置状态填入放置货物1的长方形区域中,结果如图4所示。其中货物1覆盖的小格子填写的编号都是1和货物摆放状态(图1中状态2)。
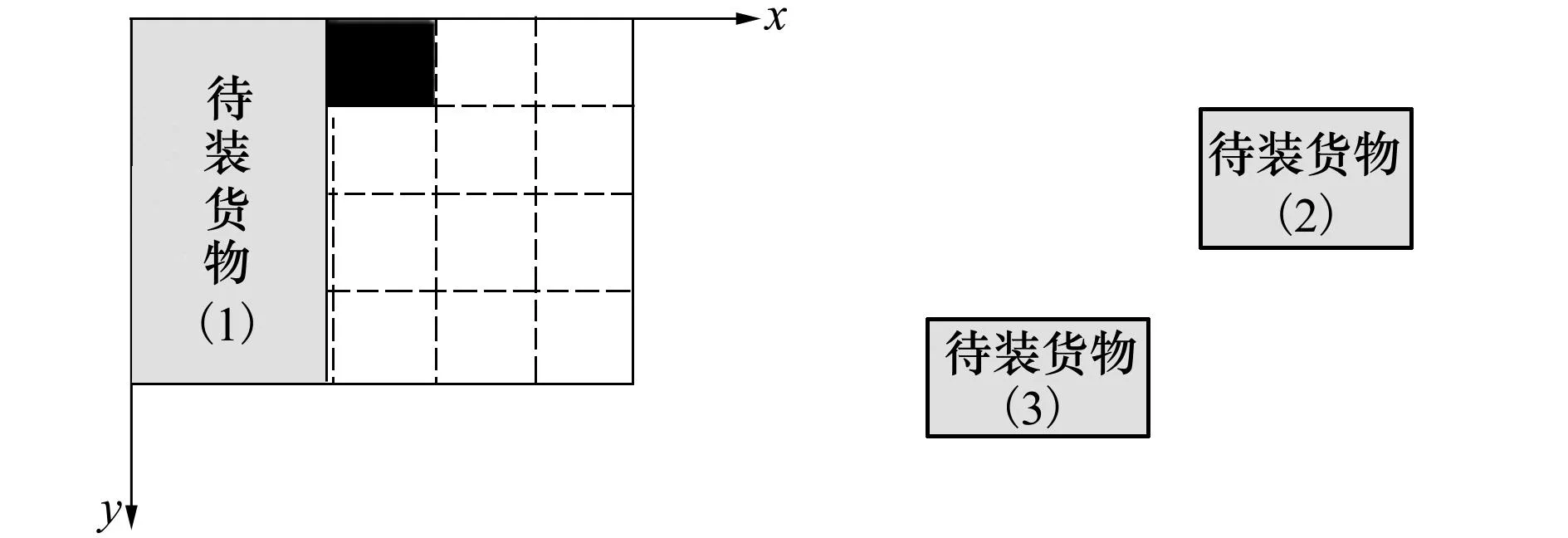
图4 装入货物1时货物的状态
接着,选择编号为2的货物进行装载,从车厢的内底面原点出发,顺着X轴寻找第一个空白小格子,如图4所示,黑色小格子为找到的第一空白小格子,从这个小格子开始顺着X轴累加,当累加长度大于等于货物2宽度时,从初始找到的空白小格子处顺着Y轴累加,当累加宽度大于等于货物2的长度时,并且货物2高度小于等于车厢内部高度时,给以小空白格子累加宽与累加长组成的长方形域填写货物编号2与货物2的摆放状态。货物3也以此方法填入车厢内底面中。最终装填状态如图5所示,从图5可以看出货物2与货物3之间存在很大间隙,可以通过增加划分的小格子个数解决。
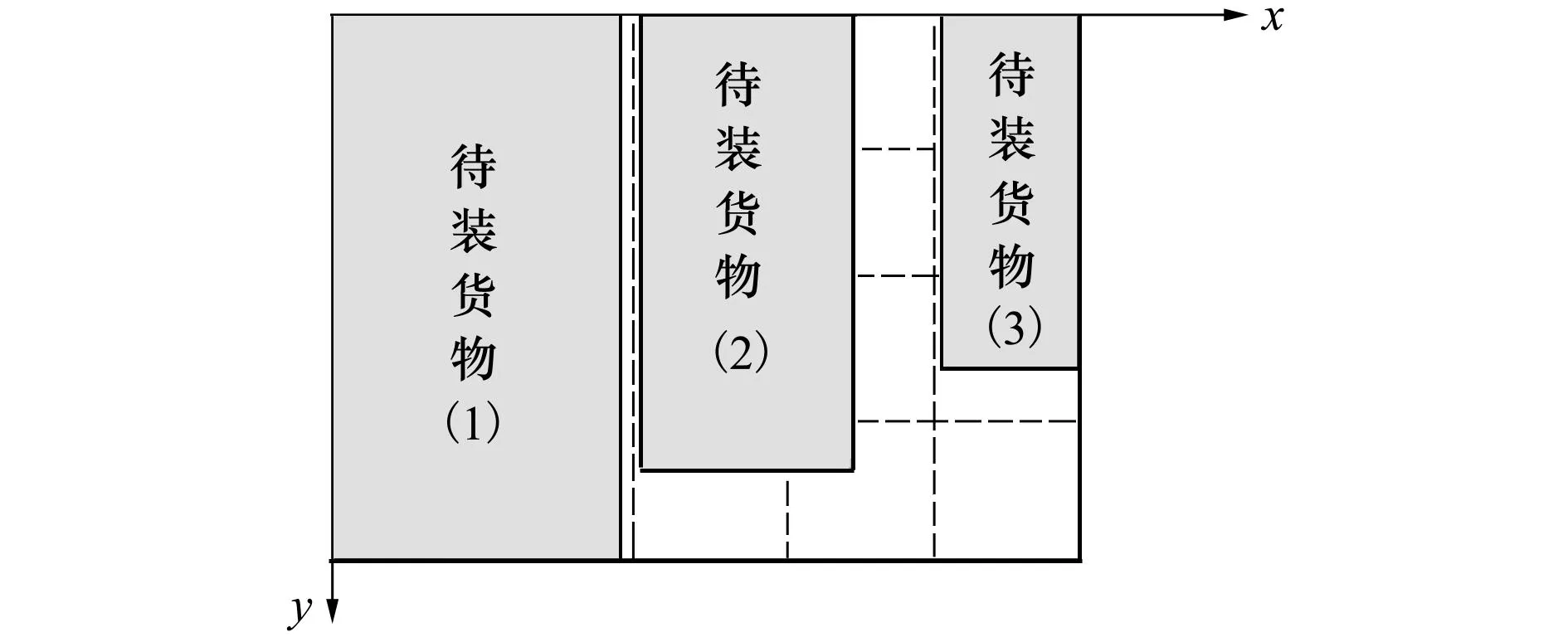
图5 最终货物装填状态
假设车厢内长为Lcarriage,车厢内宽为Wcarriage,车厢内高为Hcarriage。公式(1)与公式(2)给出当货物放置状态为图1所示第一种和第二种放置状态时,单个货物进行装载时的一般约束条件。
(1)
(2)
其中CurrentLayer为当前装载货物层数,公式(1)为如图1所示的第二种货物放置状态的一般装载约束条件,公式(2)为如图1所示的第一种货物放置状态的一般装载约束条件。
对基于平面分割理论的货物装载算法梳理为以下几个步骤:
Step1对所有的待装货物及车辆车厢进行编号,为所有待装货物设置一个装载状态标志数组,表明当前货物是否已经装载到车厢中。
Step2按照预先设置的搜索条件从待装货物中选择一个货物,利用上述所提到算法装填到车辆车厢中,若装载不成功则装填到下一个车厢中,如若成功,则在相应小空白格子中填入货物编号及货物放置状态,并设置货物对应标志数组状态为已装载。
Step3从当前未装载货物中搜索条件选择一个货物,重复Step2步骤,直到标志数组全部元素状态变为已装载。
3.2改进思想
上述提供了一种货物装载的基本思路,但是存在以下几个缺陷:
1) 进行货物装载时,只考虑了如图1所示的前2种货物放置状态,当考虑所有的货物放置状态时,算法时间成本急剧上升。
2) 算法本身带有贪婪算法的特征,致使得到的装载方案往往很难达到最优解或接近于最优解。
3) 有时在给定车辆数量的情况下,要求每个车辆装载的货物数量、质量、体积尽量达到均衡化,但通过上述算法得到的装载方案很可能不能满足此要求。
对于上述算法缺陷,提出2种改进思路。
第一个改进思路是对算法效率的改进,顺着X轴正方向搜索第一个空白小格子过程中,当开始发现不是空白小格子时,不应该继续顺序读取已添编号与状态的小格子,而是直接根据货物放置状态与货物编号跳到货物长或者货物宽占有的全部小格子的下一个小格子。这样做的好处是节省了搜索的时间,对算法效率的提高具有深远的意义。
设搜索到第一非空白小格子的时候,读取的放置状态为Status,可能取值为0或1。当Status=0时,表明货物放置状态为如图1所示第一种状态,当Status=1时,表明货物放置状态为如图1所示的第二种状态。具体的跳格步数计算公式如公式(3)所示。
(3)
式中,Lgrid为X轴正方向上划分的小格子长,X表示X轴正方向。
由于贪心算法本身具有局部搜索最优解,很难得到全局最优解的弊端,结合元启发式搜索算法-遗传算法提出第二个改进思想。
遗传算法把搜索最优解的任务交给进化过程,其关键操作包括:初始种群的设置、交叉操作,变异操作以及适应度的确定。
本文实现的是多货物多车辆车厢问题,并在车辆数量不确定的状况下,要求装载方式具有一定的伸缩性,以上述算法为基础,结合遗传算法解决货物装载问题的具体操作如下:
·染色体编码
先对货物进行顺序编码,编码为a1,a2,a3…an,其中n为货物的数量。随机生成区间在[1,6]的n个整数b1,b2,b3…bn,作为货物装载时的摆放状态。每种装载方案对应一个长度为2n的符号串,表示为P(a1,a2,a3,a4…an,b1,b2,b3…bn)。基因位a1,a2,a3…an表示货物装载的顺序,b1,b2,b3…bn表示货物装载时摆放的状态,a1,a2,a3…an与b1,b2,b3…bn一一对应,当进行装载时,按照货物编号顺序选择车厢按照平面划分理论进行填充。
·选择
选择时采用锦标赛选择算法进行选择。
·交叉
进行交叉时对货物编码和摆放状态编码分别进行交叉,由于货物编码的基因位的唯一性,货物编码交叉采用PMX部分匹配交叉法[4],摆放状态采用普通交叉方式。
·变异
由于货物编码的唯一性,所以只对基因段b1,b2,b3…bn进行随机变异。
·适应度计算
可以根据车厢承重、虚面积中空白格子占有率或者装载的均衡化程度设置相应的适应度计算公式。
可以看出,当车辆车厢变为一个时,多车厢多货物装载问题就变成了单车厢多货物装载优化问题,上述提到的遗传算法解决货物装载优化问题是基于平面分割理论的。
4实验仿真与分析
4.1实验配置
本文选用C#语言下的OpenGL函数库SharpGL对算法进行验证,SharpGL可以在Windows Forms或WPF中轻松使用OpenGL开发图形应用,借助SharpGL使用地优雅性,可以迅速建立其对装载效果的模拟仿真。
4.2实验结果与分析
本实验对基于平面分割理论算法进行了验证,实验中,设装载时具有以下约束条件:
1) 给定一批货物与一批车辆,货物及车厢形状全部是规则的长方体,车厢与货物数量不固定,要求将给定货物全部装载到给定的车辆车厢中。
2) 货物种类分为4类,第一、二、三类货物不能互相混装,第四类货物可以与前3类货物进行混装。
3) 要求货物底面接地,即实际放置状态只有如图1所示的第一、二种放置状态。
给定表1车辆车厢尺寸与表2货物尺寸,当NumLayer为1时,即只要求货物装载1层时,根据实验结果得出如表3所示的货物坐标以及放置状态,其中实验所用坐标系如图2所示。
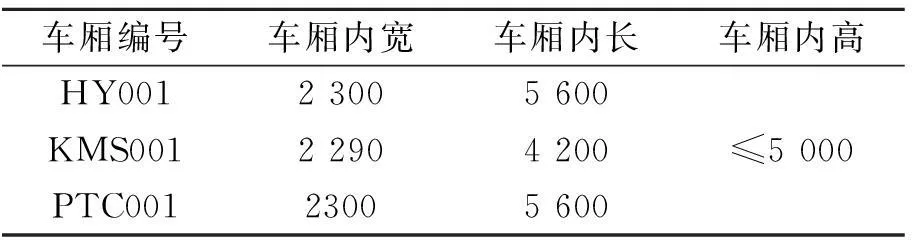
表1 给定的车辆车厢尺寸/mm

表2 给定的货物尺寸/mm

表3 生成的货物放置状态及坐标/mm
其中,货物编号、货物坐标及摆放状态所组成的五元式表示为(货物编号、货物放置的X轴坐标,货物放置的Z轴坐标,货物放置的Y轴坐标,货物放置状态)。
从实验结果可以看出,要求装载一层时,算法生成的装载方案充分利用了车厢底面空间,其中HY001车辆车厢底面空间的占有率达到90%以上,利用本算法求解自动化装载方案,在时间成本方面有明显优势。
5结论
三维货物装载问题是一个难以有效解决的NP-HARD问题,当货物装载约束条件很多时,很难得到满意的结果。本文所提出的基于平面分割的算法提供了一种货物自动化装载方案,但本算法还存在很多局限,如不能很好地利用车厢空间,对于异构货物的装载,尚不能圆满满足车厢和货物装载的约束条件。结合本算法的遗传算法解决三维货物装载问题,基于此问题,本文提出了改进思想,结合遗传算法全局搜索性可望得到最优解。不过,结合本算法的遗传算法解决三维货物装载问题,我们将会进一步给出研究与验证。
参考文献:
[1]Raymond Edward Miller, James W Thatcher. Complexity of Computer Computations[M]. New York: Plenum Press, 1972: 85-103
[2]雷定猷,陈德良. 平衡装载问题的优化模型与算法[J]. 系统工程学报, 2004,19(3): 251-257
Lei Dingyou, Chen Deliang. Optimizing Model and Its Algorithm of Balanced Loading Problems[J]. Journal of System Engineering, 2004, 19(3): 251-257 (in Chinese)
[3]Dyckhoff H. A Typology of Cutting and Packing Problems[J]. European Journal of Operational Research, 1990, 44(2): 145-159
[4]Bortfeldt A. A Genetic Algorithm for the Container Loading Problem[C]∥Proceedings of the Conference on Adaptive Computing and Information Processing, London, 1994: 25-32
[5]Bischoff E E, Ratcliff M S W. Issues in the Development of Approaches to Container Loading[J]. Omega, 1995, 23(4): 377-390
[6]李鹏,汤勇. 三维货物装箱问题的研究进展[J]. 南京林业大学学报,2015, 12(5): 1235-1238
Li Peng, Tang Yong. Research Progress of Three Dimensional Packing of Goods[J]. Journal of Nanjing Forestry University, 2015, 12(5): 1235-1238 (in Chinese)
[7]Goldberg D E. Genetic Algorithms in Search,Optimization and Machine Learning[M]. Boston, Addison-Wesley Professional,
1989
[8]Dwmkerr.SharpGL[EB/OL](2014-3-31)[2016-6-27].http:∥sharpgl.codeplex.com
Research on the Problem of Cargo Loading Based on Heuristic Algorithm
Zheng Wei1, Liu Wenxing1, Yang Xibing1, Yuan Xulong2, Wang Wenpeng1
1.School of Software and Microelectronic Engineering, Northwestern Polytechnology, Xi′an 710072, China 2.School of Marine Science and Technolgoy University, Xi′an 710072, China
Abstract:Cargo loading is a key link in the process of cargo transportation. The effective realization of rational loading of cargoes can save enormous manpower and material resources cost. But in practical work, most of the loading is directed by experience, time-consuming and unsatisfactory loading scheme ultimately. With the development of information technology, rational loading scheme can be generated automatically by computer, which can guide the actual loading. But it has been proved that the automated loading is a NP-HARD problem, how to use computer to generate automated loading to meet the constraints and possible near-optimal loading solution is a hotspot of current research. The purpose of this paper is to solve the problem of rational and efficient loading of vehicle compartments, that is, given a number of different sizes of cargoes and a number of vehicles with different sizes of compartments, automatic loading will be realized under the condition of meeting the cargo loading constraints. This paper firstly analyzes the difficulties in the realization of automatic loading by computer, then, a heuristic search algorithm based on plane segmentation theory is proposed to solve the problem of automatic loading. In order to improve the efficiency and practical value of the algorithm. This paper also puts forward the method of improving the efficiency of the algorithm. Finally, in order to accomplish the optimal loading scheme under the condition of meeting the cargo loading constraints, such as achieving a balanced loading of cargoes in a fixed number of vehicle compartments, this paper also puts forward the improved idea of combining genetic algorithm to solve the problem of cargoes loading.
Keywords:cost reduction,dimensional cargo loading, multi-vehicle, multi-cargo, plane division, genetic algorithm, heuristic algorithm
收稿日期:2016-04-14
基金项目:国家自然科学基金(61402370)与中央高校基本科研业务费专项资金资助
作者简介:郑炜(1975—),西北工业大学副教授,主要从事软件工程及软件测试的研究。
中图分类号:TP311.5
文献标志码:A
文章编号:1000-2758(2016)04-0708-06

