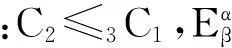覆盖空间下粗糙集和Vague软集融合方法研究

陈鹏岗, 冯晓毅, 毛晓菲



覆盖空间下粗糙集和Vague软集融合方法研究

陈鹏岗, 冯晓毅, 毛晓菲

摘要：针对覆盖近似空间下粗糙集、Vague集和软集3种不确定性理论方法融合扩展的问题，提出了一种新的基于近邻域的覆盖粗糙Vague软集模型，并讨论了相关性质。又针对该模型的不确定性度量问题，定义了一种新的覆盖粗糙Vague软集的不确定性度量方法。该方法通过引入覆盖粒度空间下知识熵的概念定义覆盖粒度空间的不确定程度，同时采用粗糙度定义覆盖粗糙Vague软集本身的粗糙性，最后将二者结合度量覆盖粗糙Vague软集的不确定性程度。算例分析表明，该度量方法是有效可行的,并且随着覆盖粒度的增大覆盖粗糙Vague软集的不确定性程度也随之增大。覆盖粗糙Vague软集模型在胃电信号(EGG)分析及胃疾病辅助诊断问题研究中有很好的应用前景。

关键词：覆盖粗糙集;Vague集;软集;不确定性

体表胃电信号(EGG)是研究胃动力学特性和功能性胃疾病诊断的重要依据。胃电是一种典型的有用信号和噪声相选加的复合信号，其检测过程中会引入大量的强背景噪声。在实际应用中，由于胃电的检测过程中存在着很多不确定性，这些先验知识往往难以获得，因此胃电的检测与分析更类似一个在不确定的环境中提取与分析未知信号的过程。近年来，基于粗糙集、Vague集、软集等不确定理论发展起来的各类融合模型为解决胃电信号数据分析等问题研究提供了强有力工具和参考模型。

实践证明，任何单一的理论和方法都很难独自解决所有问题，甚至很难全面反映和处理某一个具体问题，因此研究各种不确定模型的扩展理论及其应用问题十分必要。粗糙集[1]理论基于集合中对象间的不可分辨性，在分析处理不确定信息时无须任何先验信息，其分析方法是相对客观的。基于覆盖关系建立的覆盖粗糙集模型是对经典粗糙集模型的扩展，由于其较好的应用前景得到了研究者的广泛关注[2-7]。Vague集[8]理论作为模糊集的推广，在处理不确定性信息时比传统的模糊集有更强的表达能力及灵活性，是一种新型的处理模糊性问题的数学分析工具，有许多学者将其和其他处理不确定性信息模型结合开展研究。软集理论[9]是Moldtsov在1999年提出的一种新的处理不确定性和不精确性信息的数学工具，该理论克服了Vague集只能处理一部分不确定性信息的不足，目前在文本分类、数据挖掘、模糊决策、图像检索等领域成功应用。上述3种理论都关注信息系统中知识的不准确、不完备、不精准问题，在实际应用时既相互联系又相互补充，因此可以进行融合，以发挥各自的优势，弥补各自的不足。

因此，在研究Vague集和其他软计算理论的结合以及不确定性度量和相关应用背景问题方面，仍有大量的工作要做。针对Vague集、粗糙集和软集的结合问题，如文献[10]首次将粗糙集与软集思想进行融合，提出了粗糙软集的概念。文献[11]则将Fuzzy集与软集思想进行融合，提出了Fuzzy软集的概念。文献[12]将Vague集与软集思想进行融合，提出了新的Vague软集的基本概念并研究了相关性质、相似度量和不确定性度量等问题，但是没有研究Vague软集的相关应用问题。分析发现，类比覆盖粗糙Vague集模型，可以进一步在覆盖近似空间下将Vague软集和粗糙集进行融合，分别基于全邻域(∪Md(x))和近邻域(∩Md(x))定义2种新的覆盖粗糙Vague软集数学模型,并研究其相关性质,这是对覆盖粗糙集、Vague集和软集等理论的进一步扩展。同时,探讨Vague软集的相关应用问题也是一个重要的研究方向。另外,求属性重要性、属性核和属性约简是模糊数学理论中的几个主要问题,而不确定性度量作为各种软计算理论模型的一个重要数学特征,是上述问题的关键。

本文在上述研究的基础上,进一步在覆盖近似空间下将粗糙集、Vague集和软集3种不确定性理论方法进行融合,提出了一种全新的处理不确定信息的数学模型——覆盖粗糙Vague软集,并研究了相关性质及其不确定性度量方法,为下一步将该数学模型及其不确定性度量方法应用于胃电信号数据预处理问题奠定了相关理论基础。

1预备知识

下面对有关基础理论进行描述。

1.1粗糙集

定义1(集合的下近似和上近似)给定知识库(近似空间)K=(U,S),其中U为论域,S表示论域U上的等价关系簇,则∀X⊆U和论域U上的一个等价关系R∈IND(K),定义子集(概念或信息粒)X关于知识R的下近似和上近似分别为

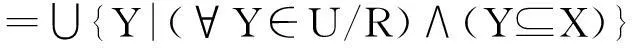
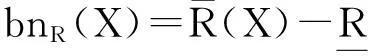
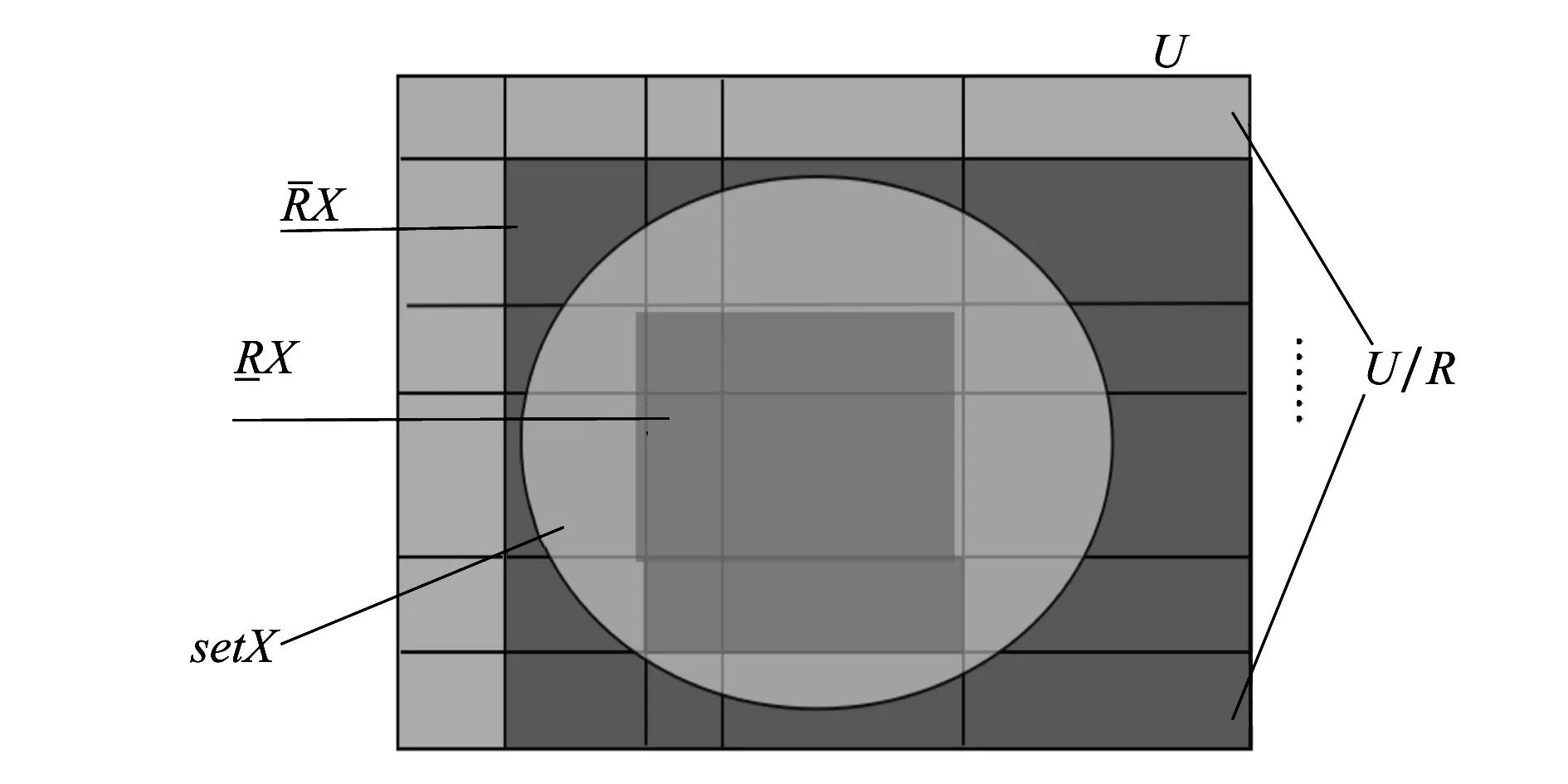
图1　集合X的上近似、下近似和边界域

1.2Vague软集

文献[13-15]提出的Vague软集模型描述如下:

定义3(Vague软集)设U是一个论域,E是一个参数集,A⊆E,且F:A→P(U)是一个映射,即∀e∈A,F(e)为U上的一个Vague集,称(F,A)为U上的一个Vague软集。

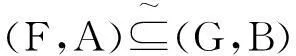
定义5(Vague软集的补集)设(F,A)为U上的一个Vague软集,称(F,A)c=(Fc,A)为(F,A)的补,其中Fc:A→V(U),具体为∀e∈A,x∈U,有tFc(e)(x)=fF(e)(x),1-fFc(e)(x)=1-tF(e)(x)。

定义6(相对空的Vague软集)设U是一个论域,E是一个参数集,A⊆E,(F,A)为U上的一个Vague软集,若∀e∈A,x∈U,tF(e)(x)=0,1-fF(e)(x)=0,则称(F,A)为U上的一个相对空的(相对于参数集A)Vague软集,记为φA。

定义7(相对全的Vague软集)设U是一个论域,E是一个参数集,A⊆E,(F,A)为U上的一个Vague软集,若∀e∈A,x∈U,tF(e)(x)=1,1-fF(e)(x)=1,则称(F,A)为U上的一个相对全的(相对于参数集A)Vague软集,记为μA。

1.3覆盖粗糙Vague集

文献[16-17]提出的覆盖粗糙Vague集模型描述如下:

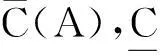
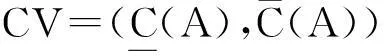
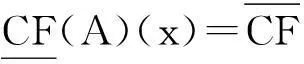
2新的覆盖粗糙Vague软集

本文在现有覆盖粗糙Vague集和Vague软集研究的基础上,进一步将2种模型融合,定义了一种新的覆盖粗糙Vague软集模型。

2.1覆盖粗糙Vague软集的定义

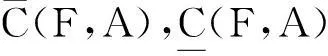
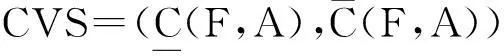
从定义9可以看出,在覆盖空间(U,C)上定义的粗糙Vague软集,表示的是在覆盖知识C上用论域上一对可定义的下近似和上近似子集来逼近所讨论的模糊对象集合, 从而可以发现模糊信息系统中一些隐藏的知识。

2.2覆盖粗糙Vague软集的性质

下面讨论覆盖粗糙Vague软集的一些重要性质。

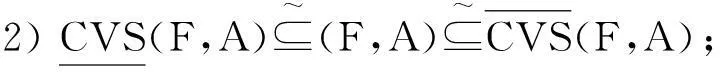
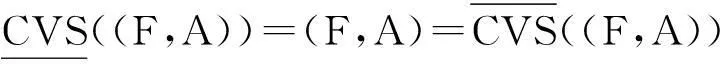
性质(1)～性质(5)依据Vague软集的相关性质证明较为简单,从略。这里仅对性质(6)和(7)进行证明,如下所示:

性质(6)的证明过程如下:

由定义3可知:

性质(7)的证明过程如下:由定义7可得

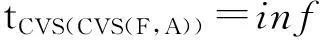
=inf{inf{t(F,A)(y)|y∈∩Md(x)}}

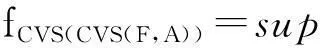
=sup{sup{f(F,A)(y)|y∈∩Md(x)}}

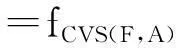
2.33种模型之间的关系

下面分别讨论Vague软集、覆盖粗糙Vague集和覆盖粗糙Vague软集的关系。3种模型都是机器学习领域处理不确定性信息的数学模型,但是根据上述3种模型的定义可以看出,Vague软集兼具Vague集和软集的代数特征,其本质是具有Vague集区间特征的软集。而覆盖粗糙Vague集兼具粗糙集和Vague集的代数特征,其本质是上下上近似算子均为Vague集的覆盖粗糙集。本文提出的覆盖粗糙Vague软集兼具粗糙集和Vague软集的代数特征,其本质是上下上近似算子均为Vague软集的覆盖粗糙集,是对覆盖粗糙Vague集和Vague软集的进一步推广和扩展。3种模型的关系如图2所示。

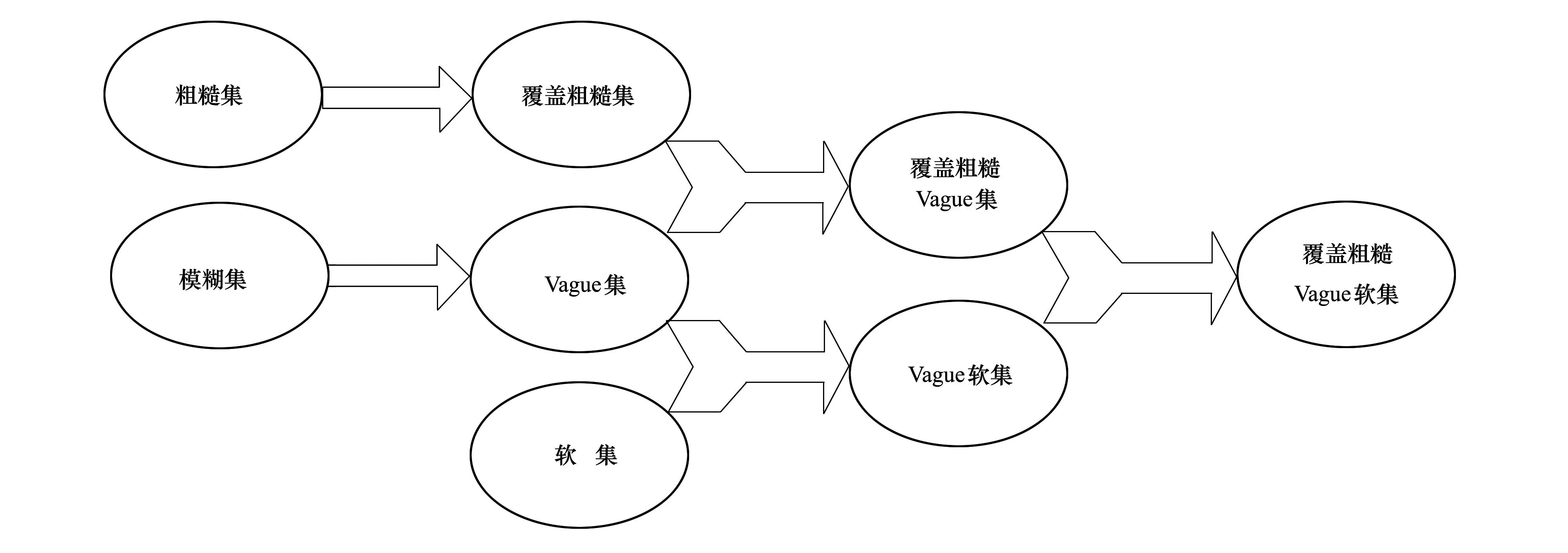
图2　3种模型之间的关系

3覆盖粗糙Vague软集的不确定性度量

引起覆盖粗糙Vague软集不确定性的因素主要有2个：①覆盖粒度空间的知识具有颗粒型。在具有较细关系的2个覆盖粒度空间上,其知识熵也具有偏序关系,即粒度空间越细,知识熵越大,覆盖粒度空间不确定性越小。反之,粒度空间越粗,知识熵越小,覆盖粒度空间不确定性越大。②其本身边界域的大小。因此类比经典粗糙集,通过覆盖粗糙Vague软集本身的代数特征来定义覆盖粗糙Vague软集本身的粗糙度。

3.1知识熵

定义10(知识熵)设U为非空有限论域,C为U上的一个覆盖,则覆盖近似空间(U,C)的知识熵定义如下:

性质2[18]设U为非空有限论域,C为U上的一个覆盖,则覆盖近似空间(U,C)的知识熵具有如下性质:

1) 0≤E(U,C)≤log|U|;

2) 当∀xi∈U(IndC(xi)=U)时,E(U,C)取最小值0;

3) 当∀xi∈U(IndC(xi)=xi)时,E(U,C)取最大值log|U|。

定理1设(U,C1)和(U,C2)为覆盖近似空间,若C1≤3C2,则有E(U,C1)≥E(U,C2)。证明参见文献[16]。

3.2覆盖粗糙Vague软集的粗糙度

定义11(覆盖粗糙Vague软集的粗糙度)

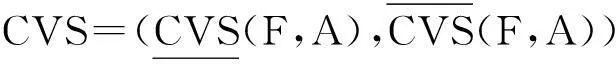
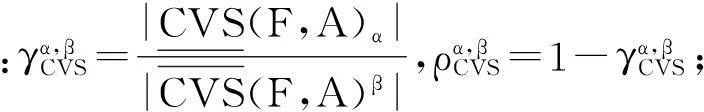
3.3覆盖粗糙Vague软集的不确定性度量方法

下面定义基于熵的覆盖粗糙Vague软集不确定性度量方法:

上述覆盖粗糙Vague软集的不确定性度量方法,既反映了覆盖粗糙空间的粒度大小也反映了覆盖粗糙Vague软集本身的粗糙度,因此可以度量覆盖粗糙Vague软集的不确定性。

4算例分析

例1设论域(U,C)为检测到的7位胃病患者xi(i=1,…,7)的1组胃电信号(EGG),用一覆盖近似空间表示,记为U={x1,x2,…,x7},将7位胃病患者随机划分为2类,分别分析每类患者胃电信号数据的不确定性,用U上的2个覆盖分别表示为

由于胃电信号(EGG)主要受电极摆放、胃的运动状态、胃壁位置变化3个参数影响,用Vague软集(F,A)表示为

知,C2≤3C1,由定义10计算知E(U,C1)=1.079;E(U,C2)=1.550,显然E(U,C1)

由覆盖粗糙Vague软集定义可得

取β=0.3,α=0.4,有

计算覆盖粗糙Vague软集不确定性度量为

5结论

本文在覆盖粗糙集理论和Vague软集理论研究的基础上，在覆盖近似空间下将粗糙集与Vague软集进行融合，提出了一种新的处理不确定性信息的数学模型-基于近邻域的覆盖粗糙Vague软集，并给出了该模型满足的各类性质及证明。另外，结合覆盖近似空间下知识熵及覆盖粗糙Vague软集粗糙度的概念，提出了一种覆盖粗糙Vague软集的不确定性度量方法，并将该模型及其不确定性度量方法应用于胃电信号分析，实验表明，覆盖粗糙Vague软集模型为胃电信号处理及胃疾病辅助诊断问题提供了良好的理论工具和数学模型。

参考文献：

[1]Pawlak Z. Rough Set[J]. International Journal of Computer and Information Sciences,l982, 11: 341-356

[2]Wang G Y, Li T R. Grzymalabusse J, et al. Rough Sets and Knowledge Technology[C]∥Proceedings of RSKT2008, Berlin, Germany, 2008

[3]Zhu W, Wang F Y. Reduction and Axiomization of Covering Generalized Rough Sets[J]. Information Sciences, 2003,152: 217-230

[4]Tsang E C C, Chen D G, Lee J W T, et al. On the Upper Approximations of Covering Generalized Rough Sets[C]∥Proceedings of the 3rdInternational Conference Machine Learning and Cybernetics, Shanghai, China, 2004: 4200-4203

[5]Zhu W, Wang F Y. On Three Types of Covering-Based Rough Sets[J]. IEEE Trans on Knowledge and Data Engineering, 2007, 19(8): 1131-1144

[6]Zhu W. Relationship between Generalized Rough Sets Based on Binary Relation and Covering[J]. Information Sciences, 2009, 179(3): 210-225

[7]Zhu W, Wang F Y. A New Type of Covering Rough Set [C]∥3rd International IEEE Conference on Intelligent Systems, London, 2006: 444-449

[8]Gau W L, Buehrer D J. Vague Sets[J]. IEEE Trans on Systems,Man,and Cybmetics,1993,23(2): 610-614

[9]Molodtsov D. Soft Set Theory-First Results[J]. Computers and Mathematics with Applications, 1999, 37: 19-31

[10] Feng F, Xiao L, Violeta L, et al. Soft Sets and Soft Rough Sets[J]. Information Sciences, 2011, 181(6): 1125-1137

[11] Feng F, Chang L, Davvaz B. Soft Sets Combined with Fuzzy Sets and Rough Sets: A Tentative Approach[J]. Information Sciences, 2010, 14(9): 899-911

[12] Wei X, Jian M, Shou W, et al. Vague Soft Sets and Their Properties[J]. Computers & Mathematics with Applications, 2010, 59(2): 787-794.

[13] 王金艳. 软集理论及其在决策中的应用研究[D]. 长春：东北师范大学，2011

Wang Jinyan. Soft Set Theory and Its Application in DeCision Making[D]. Changchun, Northeast Normal University, 2011 (in Chinese)

[14] 王昌，袁敏. Vague软集的一些代数性质[J]. 计算机工程与应用，2010，46(13)：15-21

Wang Chang, Yuan Min. Some Algebraic Properties of Vague Soft Sets[J]. Computer Engineering And Applications, 2010, 46(13): 15-21 (in Chinese)

[15] 王昌. Vague软集的相似度量及其应用[J]. 统计与决策，2012，350(2)：115-117

Wang Chang. Similarity Measurement and Application of Vague Soft Sets[J]. Statistics and Dmecision Making, 2012, 350(2): 115-117 (in Chinese)

[16] 王昌. Vague软集的模糊熵和它的一些性质[J]. 小型微型计算机系统，2012，(7)：33-35

Wang Chang. Fuzzy Entropy of Vague Soft Sets and Some of Its Properties[J]. Journal of Chinese Computer Systems, 2012,(7): 33-35 (in Chinese)

[17] 张倩倩，徐久成，胡玉文. 基于覆盖的粗糙Vague集模型研究[J]. 广西大学学报，2009，35(5)：653-657

Zhang Qianqian, Xu Jiucheng, Hu Yuwen. Study of Rough-Vague Sets Model Based on Covering[J]. Journal of Guangxi University, 2009,35(5): 653-657 (in Chinese)

[18] 徐久成，张倩倩. 覆盖粗糙Vague集的不确定性度量研究[J]. 计算机科学，2010，37(10)：225-227

Xu Jiucheng, Zhang Qianqian. Research on Uncertainty Measurement for Covering Rough-Vague Sets[J]. Computer Science, 2010, 37(10): 225-227 (in Chinese)

[19] 胡军，王国胤. 覆盖粒度空间的层次模型[J]. 南京大学学报，2008，44(5)：551-558

Hu Jun, Wang Guoyin. Hierarchical Model of Covering Granular Space[J]. Journal of Nanjing University, 2008,44(5): 551-558 (in Chinese)

[20] 杨海龙，李生刚. 软Vague关系[J]. 计算机工程与应用，2009，45(10)：1-3

Yang Hailong, Li Shenggang. Soft Vague Relation Computer[J]. Engineering and Applications,2009, 45(10): 1-3 (in Chinese)

[21] 徐菲菲，苗夺谦，李国道,等. 基于最简覆盖的粗糙模糊集的粗糙熵[J]. 计算机科学，2006，33(10)：179-181

Xu Feifei, Miao Duoqian, Li Guodao. Rough Entropy of Rough Fuzzy Sets Based on Covering[J]. Computer Science, 2006, 33(10): 179-181 (in Chinese)

[22] 王伟，彭进业，李展. 一种覆盖粗糙Vague集模型及其不确定性度量[J]. 计算机科学，2012，39(8)：228-232

Wang Wei, Peng Jinye, Li Zhan. Covering Rough Vague Sets and Uncertainty Measurement[J]. Computer Science, 2012, 39(8): 228-232 (in Chinese)

[23] 解滨，李磊军，米据生. 基于知识粒度的粗糙集的不确定性度量[J]. 计算机学报，2010，37(9)：225-228

Xie Bin, Li Leijun, Mi Jusheng. Uncertainty Measures of Rough Sets Based an Knowledge Granularities[J]. Computer Science, 2010, 37(9): 225-228 (in Chinese)

[24] 胡文彬，张宏，李千目. 基于全知熵的模式集成不确定性度量模型[J]. 南京航空航天大学学报，2012，44(4)：576-579

Hu Wenbin, Zhang Hong, Li Qianmu. Uncertainty Measure Model of Schema Integration Based on All Known Entropy[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4): 576-579 (in Chinese)

[25] 解浪，杨叶. 一种软件工作量估算的不确定性度量方法[J]. 计算机工程，2012，38(3)：276-280

Xie Lang, Yang Ye. Uncertainty Measurement Method of Software Effort Estimation[J]. Computer Engineer, 2012, 38(3): 276-280 (in Chinese)

[26] 胡军. 覆盖近似空间中粗糙集的不确定性度量研究[J]. 计算机应用与软件，2011，28(11)：376-379

Hu Jun. Uncertainty Measuring Study on Rough Sets in Covering Approximation Space[J]. Computer Applications and Software, 2011, 28(11): 376-379 (in Chinese)

Integrating of Rough Sets and Vague Soft Sets Theory in Covering Approximation Space

Chen Penggang, Feng Xiaoyi, Mao Xiaofei

(School of Electronics and Information, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Proposed in this paper is a novel covering rough Vague soft sets model based on neighbor domain and some related properties, which is applied to the problem of integrating rough sets ,Vague sets and soft sets theory in covering approximation space. At the same time, a new uncertainty measurement method is defined, which is applied to the problem of uncertainty measurement for covering rough Vague soft sets. In this method, first, the uncertainty of covering granular space based on knowledge entropy in covering granular space is defined. Next, the roughness for covering rough Vague soft sets itself is defined based on roughness. Then, the knowledge entropy in covering granular space and roughness for covering rough Vague soft sets are combinatively used to measure the uncertainty degree for covering rough Vague soft sets model. Experimental results show that this method is effective and practical, and the uncertainty degree for the covering rough Vague soft sets increase with the increase of the covering granularity. Experimental results show that the covering rough Vague soft sets has good application prospect in EGG analysis and the auxiliary diagnosis problem .

Keywords:covering rough sets; Vague sets; soft sets; uncertainty

收稿日期：2015-09-24

作者简介：陈鹏岗(1974—),西北工业大学博士研究生, 主要从事信号处理的研究。

中图分类号：TP18

文献标志码：A

文章编号:1000-2758(2016)04-0642-08