无人机快速三维航迹规划算法

尹高扬, 周绍磊, 吴青坡

(海军航空工程学院 控制科学与工程系, 山东 烟台　264001)



无人机快速三维航迹规划算法

尹高扬, 周绍磊, 吴青坡

(海军航空工程学院 控制科学与工程系, 山东 烟台264001)

摘要：针对无人机三维航迹规划的实时性问题，提出了基于快速扩展随机树的三维航迹规划方法。该算法能够根据当前环境快速有效搜索规划空间，通过随机采样点将搜索导向空白区域，使三维航迹规划能够用于实时航迹规划。通过引入航迹距离约束，搜索树将沿着路径距离最短的近似最优航迹的方向进行扩展，克服了基本快速扩展随机树方法随机性强，只能快速获得可行航迹，无法获得较优航迹的缺点。在搜索过程中无人机的航迹约束条件和地形信息得到了充分利用，使算法生成的航迹能够自动回避地形和威胁，同时满足无人机的动力学约束。通过生成的虚拟数字地图对算法进行了仿真验证，仿真结果表明该方法能够快速有效地规划出满意的无人机三维航迹。

关键词：无人机；快速扩展随机树；实时性；地形回避；三维航迹

在现代战争中，无人机所处的战场环境瞬息万变，同时由于其所执行任务的不确定性，无人机要能够根据任务过程中的实时环境信息进行在线的自主航迹规划，这对规划算法的实时性提出了很高要求[1-2]。传统的航迹规划方法是基于预先确定的代价函数生成一条具有最小代价的路径。由于无人机航迹规划的规划区域广阔，虽然近年来研究人员从规划环境建模和求解算法两方面均提出了许多改进策略，但由于规划算法强调航迹的最优性，加上要考虑无人机的性能约束等要求，传统的规划方法如遗传算法[3-4]、蚁群算法[5-6]、稀疏A*算法[7-8]、粒子群算法[9-10]等要获得一条最优路径需要很长的收敛时间和极大的内存需求，失去了在线航迹规划的现实可行性。

快速扩展随机树(RRT)方法是一种基于采样的单查询随机搜索算法，由S.M.LaValle在1998年首次提出[11]。RRT的节点扩展不需要在规划前执行预处理，能够根据当前的环境信息快速有效地搜索规划空间，在可行路径的搜索概率意义上是完全的。RRT方法已被成功应用于许多非完整系统的规划问题中，包括地面移动机器人运动规划[12]和无人机航迹规划[13]等问题。虽然基本RRT方法具有很多良好特性，但是其随机性太强，只能够保证高效快速地获取无人机的可行轨迹，无法获得较优轨迹。针对基本RRT方法的不足，研究者们从RRT方法的节点采样方式、节点扩展方式和节点选择方式3个方面对其进行了改进，取得了一定的成果[14-19]。

基本RRT及其改进方法虽然能够满足无人机在线自主航迹规划的应用要求，但是它们都是在二维平面上进行航迹搜索，因而未能利用地形的高度信息，不能有效地利用地形进行地形规避和威胁规避。本文在基本RRT方法的基础上，提出了一种三维快速航迹规划方法。并在生成的虚拟数字地形图上进行了仿真验证，实验结果表明，该方法能够充分利用地形的高程信息，有效地进行地形回避和威胁回避，是一种快速有效的三维航迹规划算法。

1问题提出

无人机三维在线航迹规划要求无人机根据预先装载的任务区的三维地形数据，规划出一条从规划起始点到目标点的三维航迹，该航迹避开了所有三维障碍物和威胁，并且满足无人机自身的飞行性能约束。无人机在惯性坐标系下的三自由度质点运动方程为：

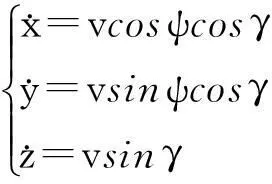
(1)

式中,(x,y,z)表示无人机在惯性坐标系中的位置;v表示无人机的速度;ψ为无人机的航向角;γ为无人机的航迹倾角。

具体来说,三维航迹规划生成的目标航迹要求满足以下几个约束条件[20]:

1) 最小航迹段长度:无人机在开始改变飞行姿态前必须保持直飞的最短距离。这一约束取决于无人机的机动能力和导航要求。

2) 最大拐弯角:无人机只能在小于或等于由自身水平平面机动性能预先确定的最大拐弯角范围内转弯。

3) 最大爬升、俯冲角:无人机只能在小于或等于由自身垂直平面机动性预先确定的上升和下滑的最大角度内爬升或俯冲。

4) 最大航迹长度:无人机的规划航迹的长度必须小于或等于一个预先设置的最大距离,它由无人机所携带的燃料以及指定任务中到达目标的允许飞行时间决定。

5) 最低飞行高度:无人机利用地形进行地形回避和威胁回避时,需要尽可能在离地面低的高度上飞行,但是飞得过低往往会增加与地面的相撞概率。一般在保持离地高度不小于某一指定高度的前提下,使飞行高度尽量降低。

只有满足了以上基本约束条件的三维航迹才是无人机的三维可行航迹。本文将这些约束条件结合到基本RRT算法中,从而得到一种快速有效的无人机三维航迹规划方法。

2基于RRT方法的三维航迹规划

基于RRT方法的航迹规划以状态空间中的规划起始点为根节点,通过随机采样逐渐增加叶节点的方式生成随机扩展树。当随机树的叶节点中包含了目标点或者目标区域的点时,随机树的扩展停止,便可在随机树中找到一条以根节点组成的从起始点到目标点的路径。RRT的扩展方式如图1所示。

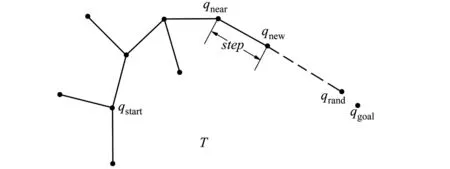
图1　RRT算法的扩展过程

图1中T表示当前存在的扩展树,qrand表示状态空间中的随机采样点,qnear表示离随机采样点qrand最近的一个树节点,然后在qrand和qnear的连线上以扩展步长step为单位截取一个新节点qnew,如果在向新节点qnew行进的过程中没有碰到障碍物,则将应qnew加入到扩展树中,否则需要重新选择为qrand。继续迭代计算直到qnew到达目标区域则算法结束,此时可以在扩展树T中找到一条从起点qstart到目标点qgoal的路径。

RRT算法主要包括3个部分:采样点选择;搜索扩展树上距采样点最近的节点;扩展节点。下面将从这3个部分,结合无人机的性能约束和地形高程数据,将RRT方法引入到无人机三维航迹规划。

2.1采样点选择

采样点qrand的选择不仅影响航迹质量,而且影响规划速度。三维航迹规划中采样点的随机选取原则如下:以概率p选择目标点作为采样点;以概率1-p在整个规划窗口内随机选择采样点。对于随机采样点,根据采样点的在水平面的位置信息可以查询到采样点的高程信息。令随机采样点在水平面的投影坐标为(xrand,yrand),则随机采样点的高程信息为z(xrand,yrand)。令无人机的最低飞行高度约束为Hmin,则随机采样点的三维坐标为qrand=(xrand,yrand,z(xrand,yrand)+Hmin)。

2.2节点扩展

通过随机采样点qrand,可以找出已存在扩展树T的树节点q中离随机采样点距离最近的一个树节点qnear,使得

(2)

在qnear和qrand的连线上,计算从qnear以最小航迹段长度L到达的新点qnew

(3)

令qnew的坐标为(xnew,ynew,znew),qnear的坐标为(xnear,ynear,znear),qnear的根节点为qnear-root(xnear-root,ynear-root,znear-root)。qnew必须满足避障和无人机自身性能约束的条件下才能加入到扩展树T中。

1) 最大拐弯角约束

如图2所示,令航迹段qnear-rootqnear和qnearqnew的水平投影分别为

设最大允许拐弯角为θ,则qnew必须满足

(4)

图2　拐弯角约束示意图

2) 最大爬升/俯冲角约束

如图3所示,航迹段qnearqnew的坐标为

设最大爬升、俯冲角为φ,则qnew必须满足

(5)

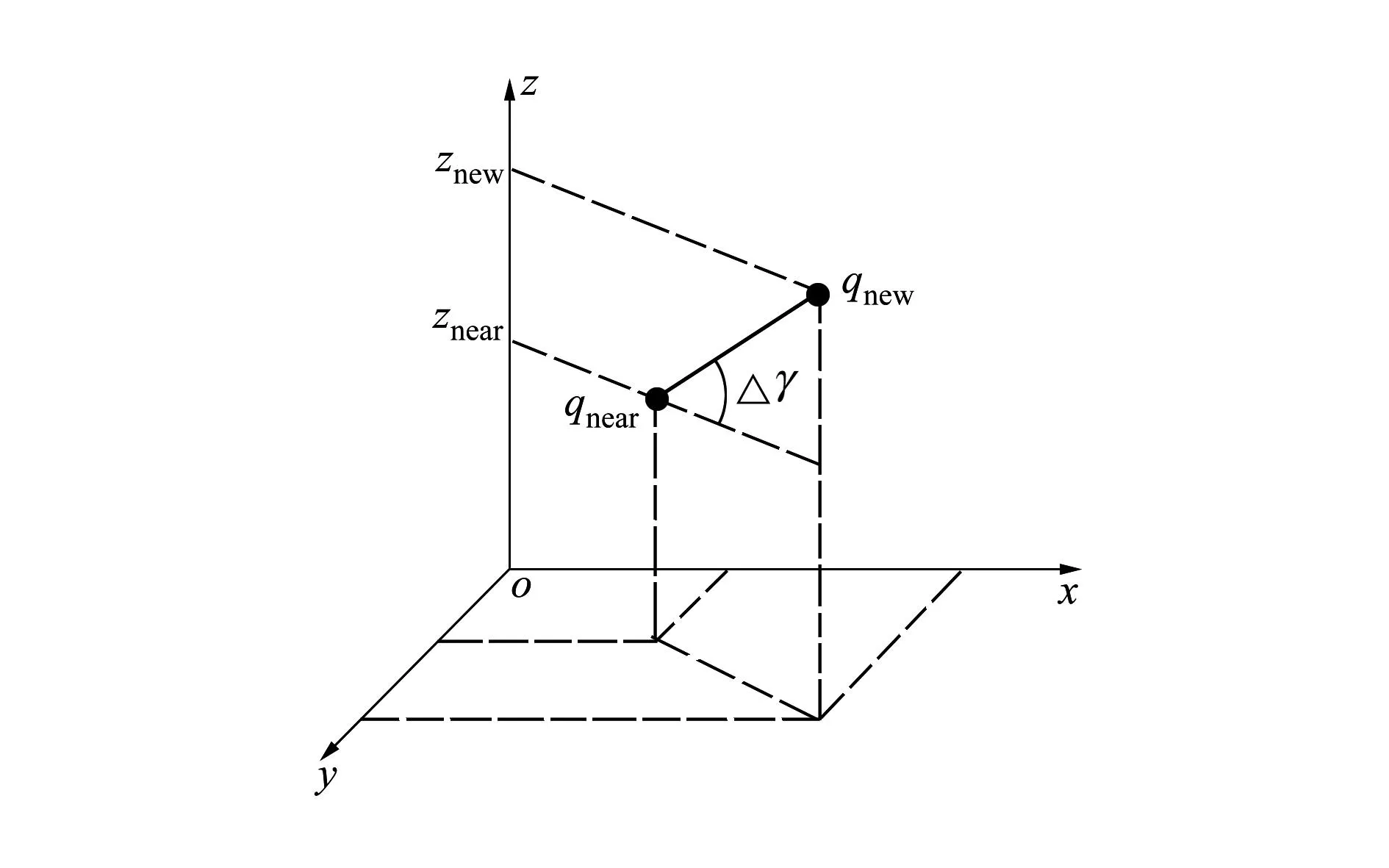
图3　爬升角约束示意图

3) 最大航迹长度

最大航迹长度是无人机的航迹距离约束,它取决于无人机的燃料载荷和任务执行时间的限制,记为dmax。节点扩展过程中长度大于这个距离的航迹认为是无效航迹,新节点为无效点。该约束在二维空间的投影表示如图4所示。新的扩展节点qnew,通过追溯根节点得到从起始点到qnew的航迹距离为D(qnew),图中黑色粗实线航迹。SL(qnew)是从扩展节点qnew到目标点qgoal的欧氏距离。只有当满足D(qnew)+SL(qnew)≤dmax时,才能把qnew加入到已有的扩展树T中。

图4　最大航迹长度约束

2.3冗余扩展点剪裁

由于RRT方法是一种随机方法。在RRT方法产生的可行航迹中可能会包含冗余的节点。去除冗余的航迹节点,可以缩短无人机的航迹长度,减少无人机的机动次数。

设经过RRT方法求得的可行路径的节点序列为{wp1,…,wpn},其中wpn为目标点位置。记经过冗余节点剪裁后的节点序列为φ,φ初始为空。令j=n,首先将目标点wpj添加到φ中。对于i∈[1,…j-1],循环检查(wpj,wpi)之间的连线是否存在障碍或者威胁,是否存在不满足无人机自身性能约束的情况。如果存在,则令i=i+1;否则,只要检测出第一个不违背条件的节点wpi就停止循环,令j=i,并将wpi添加到φ中。重复上述循环,直到j=1时结束。

2.4算法描述

基于RRT方法的三维航迹规划算法的具体步骤如下:

1) 以无人机当前位置作为规划起始点qstart,初始化搜索树T。

2) 以概率p选择目标点作为采样点;以概率1-p在整个规划窗口内随机选择采样点qrand。

3) 通过随机采样点qrand,找出已存在扩展树T的树节点q中离随机采样点距离最近的一个树节点qnear。在qnear和qrand的连线上,计算从qnear以最小航迹段长度L到达的新点qnew。

4) 判断qnew是否满足避障和文中所述无人机自身性能约束,若满足,则将qnew加入到扩展树T中。否则转到步骤 2)。

5) 判断|qnew-qgoal|≤L,若满足,转到步骤6),否则转到步骤 2)。

6) 通过形成的扩展树T,获得从起始点qstart到终点qnear的可行路径。

7) 对冗余航迹节点进行剪裁,得到最终航迹。

3数字地图数据的模拟

通过对实际地形的研究,一定范围内的地形特性,可以通过地形高度均值、地形起伏的均方差及地形点之间的抗相关系数来描述[21]。

地形的高程可以表示为

(6)

式中,H(x,y)为(x,y)点的实际高度;H0为该地区的平均高度;Z(x,y)为地形平均高度基础上的地形起伏高度。

3.1随机地形的模拟

实际地形的起伏可以表征为高斯分布的随机序列。文中采用通用的两维一阶离散自递推过程进行求解,即

(7)

(8)

(9)

(10)

式中，Std为地形起伏高度的均方差;τxc和τyc分别为x方向和y方向上的抗相关距离。

两维离散自递推过程需要有2个一维随机过程产生该地区随机地形在x方向和y方向上的地形边界的初始条件,即

(11)

(12)

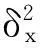
(13)

(14)

(15)

(16)

3.2山峰的模拟

文中使用多项式产生地形数据,模拟山峰地形:

式中，Zi为基准地形高度Z0上的第i个山峰的高度;x0i、y0i是第i个山峰的坐标;xsi、ysi分别是与第i座山沿x方向和y方向上的与坡度有关的量。

4仿真实验

4.1仿真参数设置

基于上述算法设计,在Intel 2.5 GHz 主频,8GB内存的普通PC机上使用MATLAB编程进行算法仿真实验。无人机执行任务区域的地形为1 001×1 001(无量纲)大小的由上述数字地图的模拟算法生成的虚拟三维地形图和模拟威胁地图。地形高度均值为0;地形起伏方差为50;该地形在x方向和y方向上抗相关距离均为300。5座模拟山峰在坐标(400,500)、(600,800)、(600,200)、(350,200)和(300,300)处,山峰高度分别为450、300、400、400和300;1个模拟湖泊位于坐标(500,100)处,深度为150;2个防空导弹威胁区位于坐标(330,750)和(750,500)处,用半球体表示,球体半径均为200。无人机的最大转弯角为60°;最大爬升/俯冲角为30°;最低飞行高度为50;最小航迹段长度为100。

4.2仿真结果

图5～图6和表1显示了规划起始点坐标为(10,10,49),目标点坐标为(900,900,0)进行的试验1的结果。图5中最大航迹约束dmax取值为起始点到目标点的直线距离S的1.3倍;而图6中采用一个较大的dmax,取值为起始点到目标点的直线距离S的2倍。图中a)为规划航迹的三维显示结果。b)为规划航迹航路点的高度与该点地形高度对比。图7、图8和表2显示了规划起始点坐标为(10,900,49),目标点坐标为(900,10,50)进行的试验2的结果。

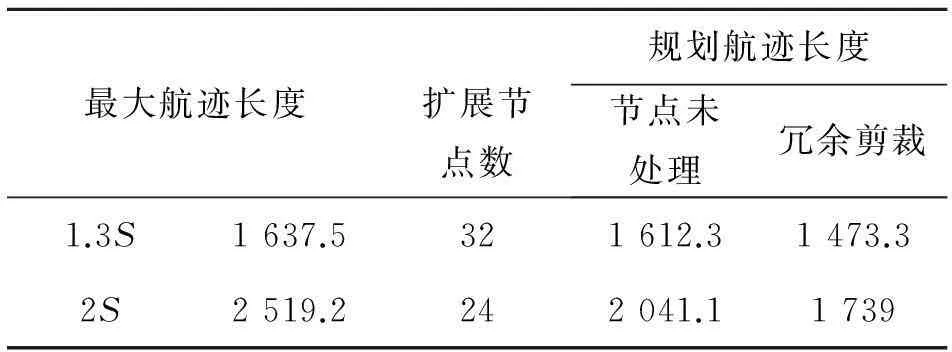
表1　试验1数据

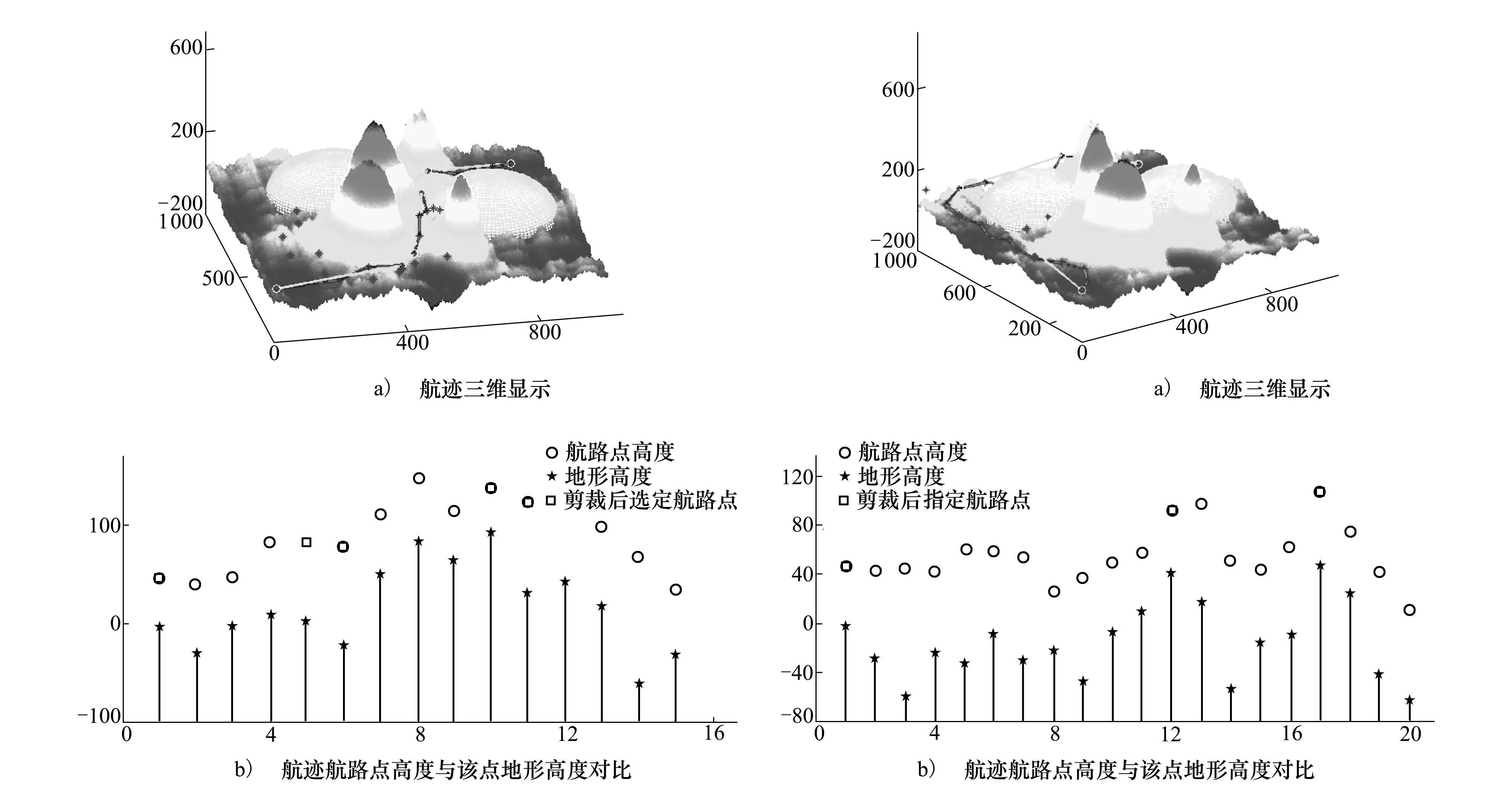
图5　试验1中采用小dmax值规划的结果　　　　图6　试验1中采用较大dmax值规划的结果

图7　试验2中采用小dmax值规划的结果　　　　　图8　试验2中采用较大dmax值规划的结果

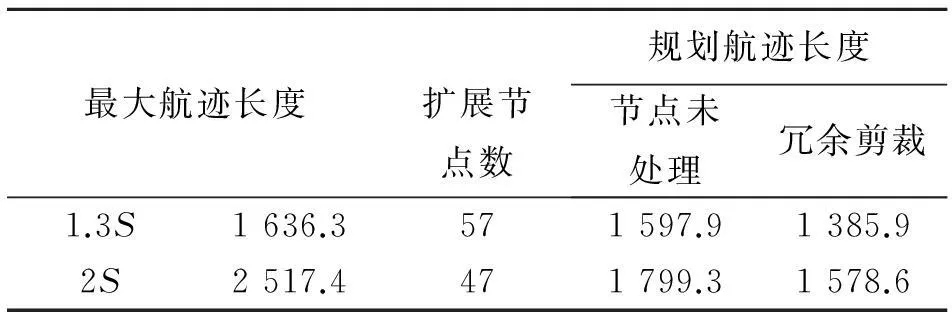
最大航迹长度扩展节点数规划航迹长度节点未处理冗余剪裁1.3S1636.3571597.91385.92S2517.4471799.31578.6

实验结果表明，基于RRT方法的三维航迹规划算法对于不同的规划起始点和目标点均能够快速地规划出满足地形、威胁回避和无人机自身性能约束条件的可行航迹，通过对冗余节点的剪裁，可以去除不必要的航迹点，缩短了规划航迹的长度。对于相同的规划起始点和目标点，通过引入航迹距离约束，限制了生成路径中可能的转弯次数，减少了可扩展节点，提高了搜索效率，同时以一定概率选择目标点作为采样点来加强搜索过程中的启发信息，搜索树将沿着路径距离最短的近似最优航迹的方向进行扩展。该算法克服了基本RRT方法随机性强，只能快速获得可行航迹，无法获得较优航迹的缺点。

5结论

本文针对无人机自主航迹规划的实时性问题，提出了基于RRT方法的三维快速航迹规划算法。该算法继承了RRT方法用于航迹规划的快速性，同时将地形信息和无人机的自身性能约束结合到扩展树的节点扩展中，使得规划出来的航迹能够满足实战要求。通过引入航迹距离约束，增加启发信息克服搜索的随机性，使得规划出的可行航迹接近最优航迹，有效地提高了无人机自主航迹规划的时间性能，兼顾了航迹规划的最优性与实时性。

参考文献：

[1]沈林成,牛轶峰,朱华勇. 多无人机自主协同控制理论与方法[M]. 北京: 国防工业出版社, 2013

Shen L C, Niu Z F, Zhu H Y. Theories and Methods of Autonomous Cooperative Control for Multiple UAVs[M]. Beijing, National Defense Industry Press, 2013: 109-110 (in Chinese)

[2]沈林成,陈璟,王楠. 飞行器任务规划技术综述[J]. 航空学报, 2014, 35(3): 593-606

Shen L C, Chen J, Wang N. Overview of Air Vehicle Mission Planning Techniques[J]. Acta Aeronoutica et Astronautica Sinica, 2014, 35(3): 593-606 (in Chinese)

[3]Zheng C W, Ding M Y, Zhou C P. Real-Time Route Planning for Unmanned Air Vehicle with An Evolutionary Algorithm[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2003, 17(1): 63-81

[4]何珮,屈香菊,武哲. 应用自适应遗传算法进行参考航迹规划[J]. 航空学报, 2003, 24(6): 499-502

He P, Qu X J, Wu Z. Aircraft Referenced Flight Path Planning by Using Adaptive Genetic Algorithms[J]. Acta Aeronoutica et Astronautica Sinica, 2003, 24(6): 499-502 (in Chinese)

[5]Chen M, Wu Q X, Jiang C S. A Modified Ant Optimization Algorithm for Path Planning of UCAV[J]. Applied Soft Computation, 2008, 8(4): 1712-1718

[6]Duan H B, Zhang X Y, Wu J. Max-Min Adaptive Ant Colony Optimization Approach to Multi-UAVs Coordinated Trajectory Replanning in Dynamic and Uncertain Environments[J]. Journal of Bionic Engineering, 2009, 6(2): 161-173

[7]李春华,郑昌文,周成平. 一种三维航迹快速搜索方法[J]. 宇航学报, 2002, 23(3):13-16

Li C H, Zheng C W, Zhou C P. Fast Search Algorithm for 3D-Route Planning[J]. Journal of Astronautics, 2002, 23(3): 13-16 (in Chinese)

[8]Wang Z, Liu L, Long T. Enhanced Sparse A*Search for UAV Path Planning Using Dubins Path Estimation[C]∥Proceedings of the 33rdChinese Control Conference, Nanjing, 2014: 738-742

[9]Li S B, Sun X X, Xu Y J. Particle Swarm Optimization for Route Planning of Unmanned Air Vehicles[C]∥Proceedings of the Congress on Information Acquisition. Weihai, 2006: 1213-1218

[10] Fu Y G, Ding M Y, Zhou C P. Routing Planning for Unmanned Aerial Vehicle(UAV) on the Sea Using Hybrid Differential Evolution and Quantum-Behaved Particle Swarm Optimization[J]. IEEE Trans on Systems, Man, and Cybernetics: Systems, 2013,43(6): 1451-1465

[11] LaValle S M. Rapidly-Exploring Random Trees: A New Tool for Path Planning[R]. Computer Science Department, Iowa State University, 1998

[12] 周金良,黄彦文,曹其新. 对抗环境下足球机器人路径规划[J]. 上海交通大学学报, 2006,40(11):1827-1831

Zhou J L, Huang Y W, Cao Q X. The Path Planning for Robot Soccer Under Antagonistic Environment[J]. Journal of Shanghai Jiaotong University, 2006,40(11): 1827-1831 (in Chinese)

[13] Amin J N, Boskovic J D, Mehra R K. A Fast and Efficient Approach to Path Planning for Unmanned Vehicles[C]∥Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit. Keystone, 2006

[14] Kuffner J J, LaValle S M. RRT-Connect: An Efficient Approach to Single-Query Path Planning[C]∥Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, 2000:995-1001

[15] Kalisiak M, Panne M. RRT-Blossom: RRT with a Local Flood-Fill Behavior[C]∥Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Florida, 2006: 1237-1242

[16] Melchior N A, Simmons R. Particle RRT for Path Planning with Uncertainty[C]∥Proceedings of the IEEE International Conference on Robotics and Automation, Roma, 2007: 1617-1624

[17] 彭辉,王林,沈林成. 区域搜索中基于改进RRT的UAV实时航迹规划[J]. 国防科学技术大学学报, 2009, 31(5): 86-91

Peng H, Wang L, Shen L C. The Modified RRT-Based Real-Time Route Planning for UAV Area Target Searching[J]. Journal of National University of Defense Technology, 2009, 31(5): 86-91 (in Chinese)

[18] Bruce J, Veloso M. Real-Time Randomized Path Planning for Robot Navigation[C]∥Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Lausanne, 2002: 2383-2388

[19] Yershova A, Jaillet L, Simeon T. Dynamic-Domain RRTs: Efficient Exploration by Controlling the Sampling Domain[C]∥Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, 2005: 3851-3861

[20] 丁明跃,郑昌文,周成平,严平. 无人飞行器航迹规划[M]. 北京: 电子工业出版社, 2009

Ding M Y, Zheng C W, Zhou C P, Yan P. Route Planning for Unmanned Aerial Vehicles[M]. Beijing, Publishing House of Electronics Industry, 2009: 41-43 (in Chinese)

[21] 叶文,范洪达,朱爱红. 无人飞行器任务规划[M]. 北京: 国防工业出版社, 2011

Ye W, Fan H D, Zhu A H. Mission Planning for Unmanned Aerial Vehicles[M]. Beijing, National Defense Industry Press, 2011: 42-47 (in Chinese)

Efficient Path Planning Algorithm in Three Dimensions for UAV

Yin Gaoyang, Zhou Shaolei, Wu Qingpo

(Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Abstract:To satisfy the real-time requirement of path planning in three dimensions for unmanned aerial vehicle, a path planning algorithm based on rapidly-exploring random tree is proposed. By random sampling point in configuration space, the search will be guided to empty area, thus the algorithm can search the high-dimension space quickly and efficiently according to the current environment, which can be used in real-time path planner. By introducing the path length constraint, the search tree will explore along the direction of the near optimal path. The proposed algorithm overcomes the disadvantage of basic RRT algorithm that only to quickly get feasible path, unable to obtain near optimal path. During the search process, the path constraints of UAV and the terrain information are fully utilized, so that the path generated by the algorithm can avoid terrain and threat automatically, and meet the dynamic constraints of UAV. Simulations for the algorithm are made on a generated virtual digital map. Simulation results demonstrated that this proposed method can complete path planning mission in three dimensions quickly and effectively.

Keywords:unmanned aerial vehicle (UAV); rapidly-exploring random tree; real-time; terrain avoidance; 3D-path

收稿日期：2016-02-12

基金项目：航空科学基金(20135184007)资助

作者简介：尹高扬(1987—)，海军航空工程学院博士研究生,主要从事导航、制导与控制的研究。

中图分类号：V249.1

文献标志码：A

文章编号:1000-2758(2016)04-0564-07