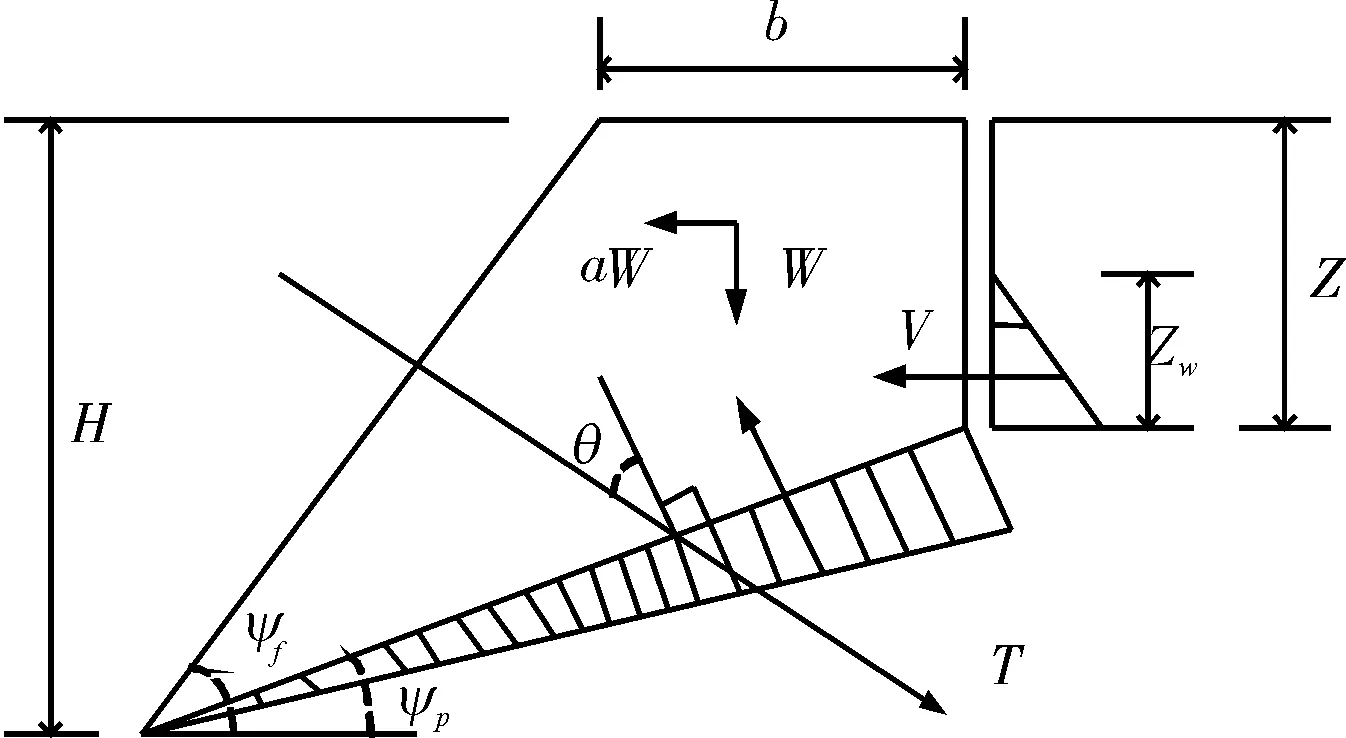
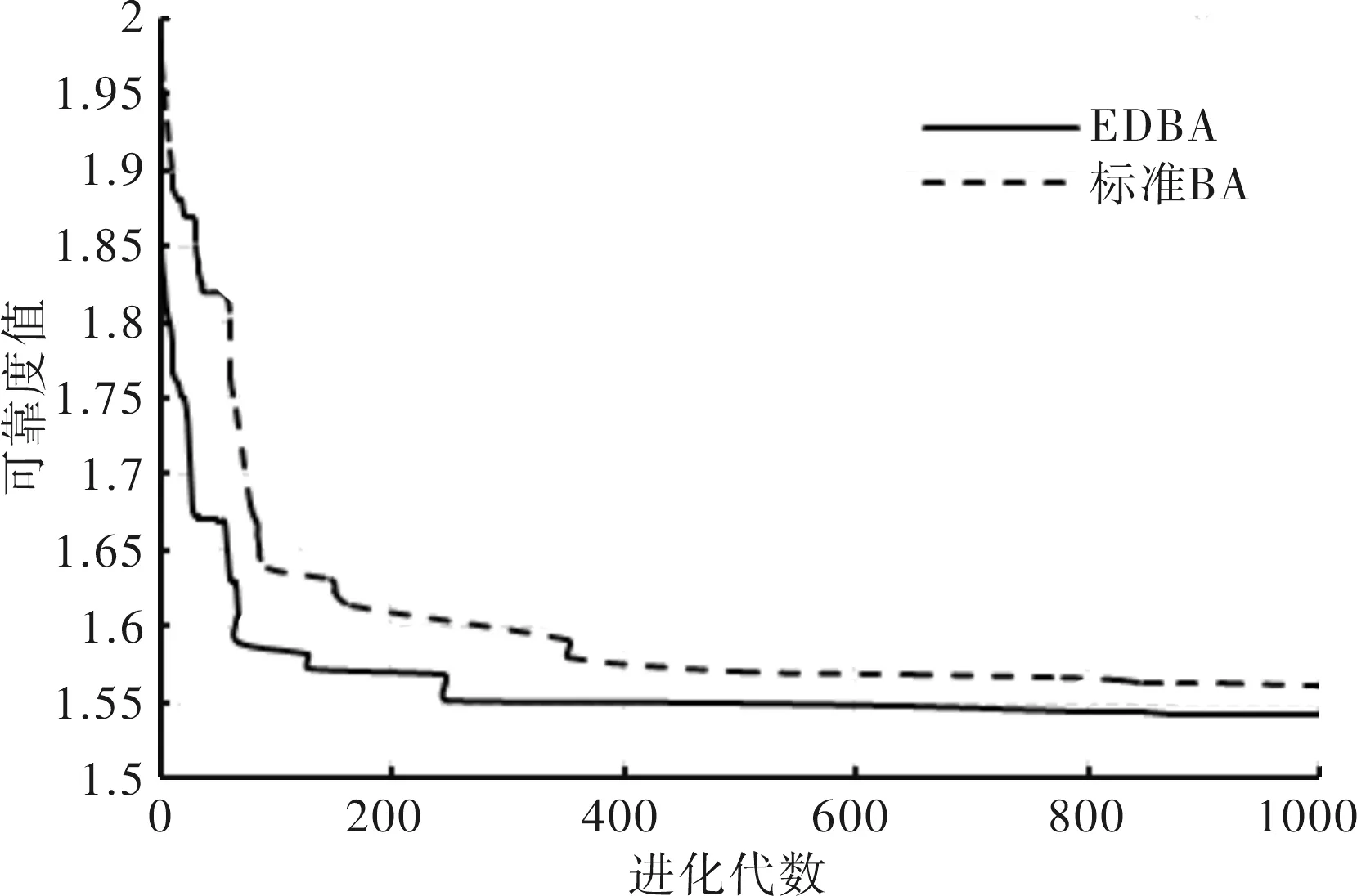
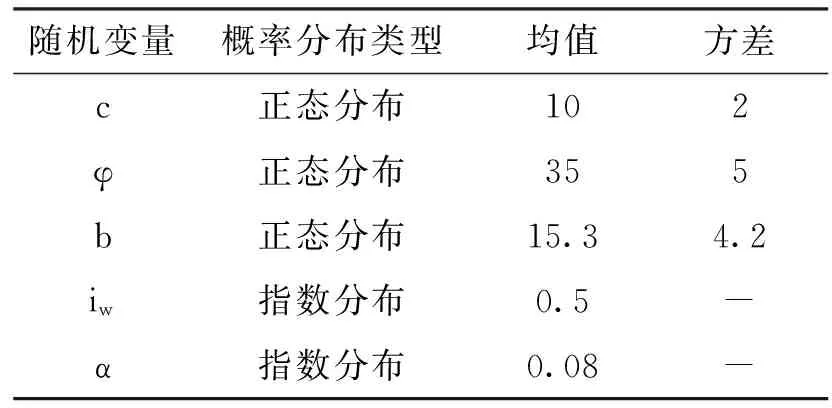
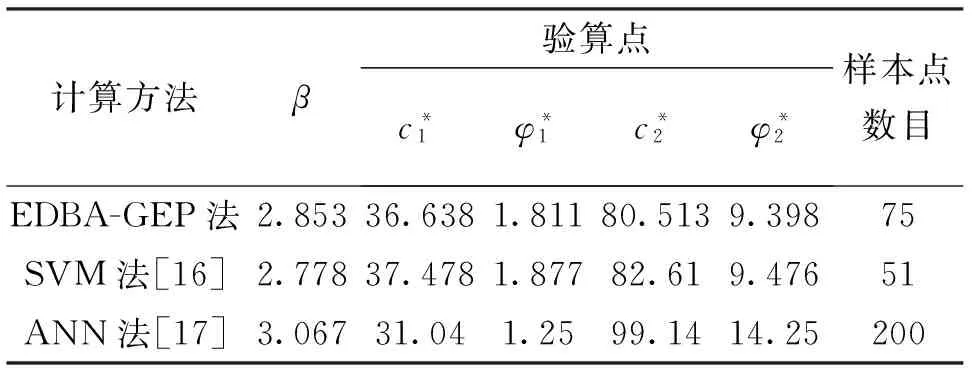
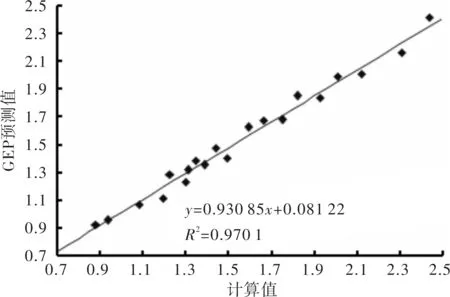
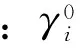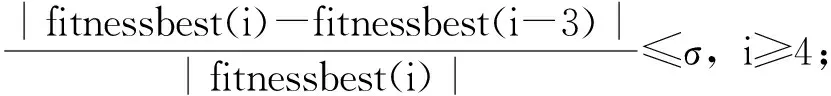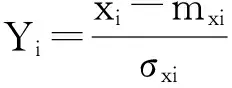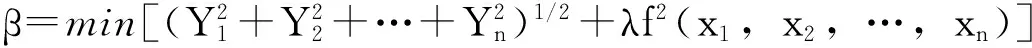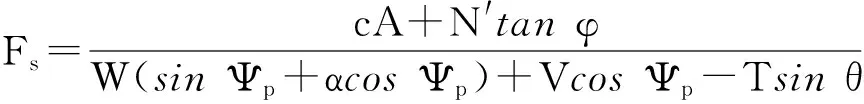蝙蝠优化算法在边坡可靠性分析中的应用*

贺子光，吴　博，赵法锁，程振全，汪班桥，段　钊

(1.长安大学 地质工程与测绘学院，陕西 西安 710054； 2.西安科技大学 地质与环境学院，陕西 西安 710054)



蝙蝠优化算法在边坡可靠性分析中的应用*

贺子光1，吴博1，赵法锁1，程振全1，汪班桥1，段钊2

(1.长安大学 地质工程与测绘学院，陕西 西安 710054； 2.西安科技大学 地质与环境学院，陕西 西安 710054)

摘要:基于可靠度的几何意义，提出基于蝙蝠算法(Bat Algorithm, BA)进行边坡可靠性分析。针对基本蝙蝠算法易早熟、收敛精度低的不足，将细菌觅食算法中的迁徙操作(Elimination Dispersal)引入基本蝙蝠算法，形成迁徙蝙蝠算法(EDBA)，提高了算法的全局搜索能力和收敛速度。算例1的计算结果表明：EDBA较基本BA的计算精度高，收敛速度快，稳定性更好，对求解复杂、高度非线性功能函数的可靠性问题具有很好的适应性。对于隐式功能函数的边坡可靠度求解，提出了采用蝙蝠算法和基因表达式编程(Gene Expression Programming, GEP)相结合的计算边坡可靠度的新方法。该方法采用GEP方法拟合边坡极限状态函数，构建响应面，通过蝙蝠算法计算边坡可靠度及相应的验算点；算例2的计算结果证明：EDBA-GEP方法对求解隐式功能函数的边坡可靠性问题具有很好的适应性，是科学可行的，具有很好的应用前景。

关键词:基因表达式编程(GEP)；蝙蝠算法(BA)；迁徙因子；响应面法(RSM)； 边坡；可靠度

在边坡工程评价、设计和施工过程中，最重要、最根本的指标是边坡的安全性，由于岩土工程的不确定性中，传统的边坡稳定性评价方法不能很好地解决该问题。鉴于此，边坡的可靠性分析理论得到了迅速发展，它的分析结果能够反映各种类型的不确定性或随机性，更能客观地评价边坡的安全性。

经过国内外众多学者的研究，边坡可靠性分析方法取得了一定的成果。目前，用于边坡可靠度计算的方法主要有：蒙特卡罗法(MCS)[1]、一次二阶矩法(FORM)[2]、最优化法[3]和响应面法(RSM)[4]等，但这些方法均存在一些或多或少的缺陷：MCS是最简单、最直接的可靠度分析方法，回避了可靠度指标计算中的数学困难，不需要考虑极限状态函数的复杂性，但是对失稳概率小的边坡问题，其计算效率低下，非常耗时；最优化法是一种新的求解可靠度指标的数值方法，即求解可靠指标等同于求解极限状态曲面到原点最短距离的优化问题。应该说用优化方法求解可靠指标是一种有效的途径，但现有的大部分优化方法在求解功能函数呈高度非线性问题时，有时会陷入局部最小值，或者是计算结果不收敛，效果往往不理想；RSM通过多项式函数拟合技术构造响应面代替隐式功能函数，在确定性方法和可靠性分析之间建立了“桥梁”，但传统的响应面法在某些特殊情况下还存在收敛困难的问题。后来，有学者将ANN法和SVM法应用于边坡可靠性分析中，然ANN法存在局部极小和“过拟合”问题；SVM法的拟合精度受所选核函数参数取值的影响较大，而其参数是通过优化方法得到，不同的参数优化方法导致其拟合精度不同。因此，寻求合适的边坡可靠度分析方法仍是一个亟待解决的问题。

蝙蝠算法(Bat Algorithm，BA)是一种模拟蝙蝠觅食行为的新型元启发示优化算法[5]，已在工程设计、分类等领域得到应用，研究表明，BA对高度非线性优化问题有着很好的解决能力。基因表达式编程(Gene Expression Programming，GEP)是Ferreira在生物基因表达的启示下[6]，融合了GA和GP优点的新函数挖掘方法。GEP方法具有很强的函数拟合能力，在函数拟合时不需要任何先验知识，结合多数据流之间的映射关系，是一种新型多数据流的拟合方法。因此本文提出将BA和GEP结合，应用于边坡可靠性分析中，通过GEP构建显式的极限状态函数，利用BA进行可靠度指标计算。

1EDBA-GEP方法

1.1基本蝙蝠算法

蝙蝠在不同程度上都有回声定位系统，因此有“活雷达”之称。借助这一系统，它们能在完全黑暗，且存在大量干扰的环境中飞行和捕捉食物。蝙蝠能连续不断地发出高频率超声波，如果碰到障碍物或飞舞的昆虫时，这些超声波就能反射回来，然后由它们超凡的大耳廓所接收，使反馈的信息在它们微细的大脑中进行分析。这种超声波探测灵敏度和分辩力极高，使它们根据回声不仅能判别方向，为自身飞行路线定位，还能辨别不同的昆虫或障碍物，进行有效的回避或追捕。根据蝙蝠的觅食特性，Xin-She Yang于2010年提出了新的种群进化算法——蝙蝠算法[7]。BA的寻优过程同粒子群算法、果蝇优化算法等类似，首先随机生成初始种群，对种群内每个个体计算相应的适应度值，然后其他个体都追随当前最优个体在空间中搜索即通过迭代找到最优解。具体的实施过程如下所示：

(1) 设置相关参数：种群规模Sizepop、最大响度值A0、初始，搜索脉冲频率范围[fminfmax] ，音量的衰减系数α，搜索频率的增强系数γ和最大迭代次数iterMax。

(2) 随机初始化蝙蝠的位置xi，并根据适应度值的优劣寻找当前最优解x*。

(3) 蝙蝠的搜索脉冲频率、速度和位置更新。种群在进化过程中，每一代个体的搜索脉冲频率、速度和位置按如下公式进行变化：

fi=fmin+(fmax-fmin)β

(1)

(2)

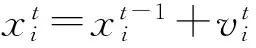
(3)

式中：fmin和fmax分别为蝙蝠发出声波的最小和最大频率，β为[0,1]中的均匀随机数。设置初始值时，每只蝙蝠发射声波的频率服从于[fmin,fmax]的均匀随机分布。

(4) 生成随机数rand1>ri，则从处在最佳位置的蝙蝠群体中选择1个，对蝙蝠进行随机扰动，用扰动后的位置取代蝙蝠当前的位置x*。

Xnew=Xold+εAt,

(4)

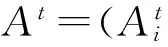
(5) 生成随机数rand2，如果rand2>Ai且f(xi)

(5)

(6)

(6) 依据适应度值的大小对群体蝙蝠进行排序，找到当前最优位置x*。

(7) 判断是否满足停止条件，若满足，则结束算法并输出最优解，否则转到步骤2。

1.2蝙蝠算法的改进

1.2.1引入细菌迁徙因子

尽管BA具有很多其他算法不具有的优点，但是由BA的原理可知，在整个迭代寻优过程中，一旦选取出当代最优个体，所有的个体都是根据最优个体的位置更新自身的速度，因此降低了种群的多样性。假如最优个体为局部最优解，则整个进化过程易发生“早熟”收敛现象，导致算法陷入局部最优解。针对该问题，本文将细菌觅食算法中的迁徙操作因子引入基本BA中，形成迁徙蝙蝠算法(Elimination Dispersal Bat algorithm，EDBA)[8-10]。新算法采用进化停滞步数t作为执行条件，假设细菌的迁徙概率为Ped，当t≥T(最大进化停滞步数)时，对当代种群中个体以一固定概率Ped(i)执行迁徙操作，对于适应度值高的，且靠近全局最优的个体，执行迁徙操作将会引起解的退化，因此，本文针对不同适应度值个体赋予不同的迁徙概率Ped(i)，具体见式(7)。

(7)

1.2.2改变局部搜索策略

(8)

(9)

Xnew=(ω1·Xfitbest+ω2·Xmean)+εAt。

(10)

式中：Xfitbest指当前最优解；Xmean是最优解集的平均值；ω1、ω2分别是Xfitbest和Xmean的权重，ω1+ω2=1，具体取值见式(9)。

1.3引入细菌迁徙因子的蝙蝠算法

引入细菌迁徙因子的蝙蝠算法(EDBA)以基本蝙蝠算法为依托，具体计算过程如下：

(1) 所需参数进行初始化设置，即：种群规模(Sizepop)、最大进化停滞步数限值T、脉冲发射的响度A0(i)、初始速率r0(i)，搜索脉冲频率范围[fmax,fmin]，音量的衰减系数α，最大迭代次数iterMax。

(2) 根据式(2)～(4)随机产生初始种群。

(3) 依据适应度值的大小对群体蝙蝠进行排序，记录最优适应度值fitnessbest和最差适应度值fitnessworst，并记录停滞步数t。

(4) 判断是t≥T否成立，若成立，根据式(7)计算每个蝙蝠个体的迁徙概率，采用遗传算法中的轮盘赌方式作为选择机制，将被选择个体重新分配到空间中进行寻优，未迁徙的个体保留。

(5) 对迁徙后的蝙蝠群体进行评价，根据个体适应度值的大小来更新最优解和最优值。

(6) 进行局部搜索。根据式(8)和式(9)确定ω1、ω2的取值，采用式(10)更新新解的位置。

(7) 评价新解的结果，记录当前群体中的最优位置和最优值。若当前最优位置和最优值优于以前的最优值和最优位置，则用当前最优位置和最优值替换以前的最优值和最优位置，否则保持以往的状态。

(8) 进入迭代寻优，重复步骤(2)～(7)，直至达到最大进化代数为止。

1.4GEP函数挖掘方法

GEP方法是在生物基因表达的启示下，完美地融合了GA和GP方法的优点，同时引入独特的编解码方式和头部基因约束机制，保证染色体在各种遗传操作下均能存活，增强了种群进化能力和适应能力。GEP方法同其他种群进化方法类似，演绎了生物遗传进化的机理，首先随机创建初始种群，按照独特的染色体编解码方式对初始种群进行基因表达(染色体解码)，依据所解决问题设置相应的适宜度函数，并对每个染色体进行评估。当评估结果满足进化条件，则输出结果；若否，通过一定原则或方法(例如，轮盘赌方法)选择最优个体，对所选择的最优个体进行遗传操作，产生新的子代个体，再评估。如此反复，直到得到最优解或者满足进化条件停止。

1.5响应面法

响应面法是通过一系列确定性计算，用显示的表达式来近似代替隐式极限状态函数。通过合理地选取试验点和迭代策略，来保证显示表达式函数能够在失效概率上收敛于真实的隐式极限状态函数的失效概率。响应面法为功能函数为隐式表达式的边坡可靠度计算问题提供了一条有效途径[11]，在确定性计算和随机变量之间建立了“纽带”。响应面法在使用中应注意三个问题：①响应面形式；②选择确定响应面的样本点；③迭代策略，这三个问题应根据不同情况具体分析。

2可靠度计算模型

可靠度指标β定义是：在标准正态空间中，坐标原点到极限状态曲面的最短距离。显然，不管极限状函数的具体形式如何，只要具有相同的力学或物理含义，在标准正态空间中，所表示的都是同一曲面，曲面上与坐标原点距离最近的点也只有一个，因此，可靠度指标可以转化为标准正态空间中的几何求解问题。

设具有n个正态变量x1,x2,…,xn的极限状态方程：

Z=G(x1,x2,x3,…,xn)=0。

(11)

或Z=Fs-1。

(12)

将式(11)中的变量x1,x2,…,xn标准化得：

(13)

式中：Yi为变量xi的标准正态化值，其含义为在标准正态空间中，变量xi的取值；mxi和σxi是变量xi的均值和方差。因此可靠度计算模型为：

(14)

如果随机变量服从一般分布F(xi)，则可以进行高斯变换，将一般分布变换成正态分布。高斯变换如下：

Yi=φ-1(F(xi))。

(15)

3EDBA计算可靠度

由可靠度的几何含义可知，在标准正态坐标系中，可靠度β是原点到极限状态曲面的最短距离，而验算点就是极限状态曲面上到原点距离最短的点。利用EDBA的全局搜索能力找出其到原点最短距离的点以及相应的最短距离，即可靠度和验算点，具体步骤如下所示。

(1) 对所需参数进行初始化设置，即：种群规模(Sizepop)、固定迁徙概率(Ped)最大进化停滞步数T、音量的衰减系数α，最大迭代次数iterMax。

(2) 根据式(2)～(4)随机产生初始种群。随机初始化种群中各蝙蝠的位置，其中通常将各蝙蝠的位置设置在[-3σ，3σ]区间。

(3) 约束条件处理

由于可靠度计算模型为有约束的规划模型,因此需要对约束条件进行处理，这里采用罚函数法将约束求解问题转化为无约束求解问题。

(16)

式中：f(x1,x2,…,xn)为极限状态函数，λ为惩罚因子。

(4) 计算每个蝙蝠个体的适应度值，依据适应度值的大小对群体蝙蝠进行排序，记录最优适应度值fitnessbest和最差适应度值fitnessworst，并记录停滞步数t。

(5) 判断t≥T是否成立，若成立，根据式(7)计算每个蝙蝠个体的迁徙概率，按照遗传算法中的轮盘赌方式选择个体进行迁徙操作，将选择个体重新分配到空间中进行寻优，未执行迁徙的个体保留。

(6) 对迁徙后的蝙蝠群体进行评价，根据个体适应度值的大小来更新最优解和最优值。

(7) 进行局部搜索。根据式(8)和式(9)确定ω1，ω2的取值，采用式(10)更新新解的位置。

(8) 评价新解的结果，记录当前群体中的最优位置和最优值。若当前最优位置和最优值优于以前的最优值和最优位置，则用当前最优位置和最优值替换以前的最优值和最优位置，否则保持以往的状态。

(9) 进入迭代寻优，重复步骤(2)～(8)，直至达到最大进化代数为止。

4EDBA-GEP方法计算边坡可靠度

4.1选择样本点

响应面法的计算精度受所选取样本点的影响较大,因此采用合适的样本选取方法尤为重要。统计学中，常用的取样方法有很多，各种方法均有其最为适用的范围，根据可靠度的计算特点，本文采用均匀设计法选取样本点[12-13]。在第一次响应面优化迭代时，在[-3σ，3σ]选取样本点，在后续迭代中，为了提高响应面拟合精度，应逐渐缩小选样范围。

4.2EDBA-GEP方法计算边坡可靠度

本文采用GEP方法拟合安全系数与各随机变量的显示表达式，根据拟合的显式表达式建立可靠度优化计算模型，采用EDBA计算可靠度指标及验算点。具体的实施步骤如下所示。

(1) 根据各随机变量的具体分布，在其均值处采用均匀设计法选取样本点，并通过确定性方法计算相应的安全系数。

(2) 采用GEP方法拟合安全系数与各随机变量的显式表达式。在显式表达式的基础上，建立相应的可靠度优化计算模型。

(3) 利用EDBA计算可靠度指标及相应的验算点。

(4) 判断是否满足精度要求，若否，则以当前验算点为中心点重新取样计算。如此反复迭代，直至达到预设精度停止。

5工程算例

5.1算例1：秀茂坪边坡

香港秀茂坪边坡是一典型的岩质边坡[14-15]，其稳定性主要受岩石的c，φ值影响，考虑地震和裂缝中水压对边坡的作用。剖面图如图1所示，由极限平衡条件，可得潜在滑动面上的安全系数，安全系数等于总抗滑力和总滑动力之比，随机变量为c,φ,b,iw,α，各变量含义如图1所示，采用EDBA计算该边坡的可靠度。

图1　岩质边坡剖面图

因为该边坡具有显式的安全系数表达式，因此本算例只采用EDBA计算可靠度值，并以该算例为基础，对EDBA中主要控制参数的最优组合取值进行讨论。EDBA的参数设置如下，种群规模Sizepop=40，最大进化代数iterMax=1 000、音量的衰减系数α=0.9、搜索频率的增强系数φ=0.9、固定迁徙概率Ped=0.3，最大停滞步数T=3。参数统计见表1，计算结果见表2，计算结果数据分析见表3。优化过程见图2。

图2　EDBA和基本BA的优化过程

(17)

式中：

A=(H-z)/sinΨp;

b=(H-z)cotΨp-Hcotψf

U=0.5γwZwA;

z=H-(b+Hcotψf)tanψp;

N=W(cosψp-αsinψp)-U-Vsinψp+Tcosθ;

H=60m,ψf=50°,ψp=35°,T=0,γw=1.0kN/m3;

γ=2.6kN/m3。

表1　随机变量及其统计参数

表2　边坡可靠度的计算结果

首先引入“寻优成功率”概念，若|si-最优值|/最优值≤ξ，则称第i次寻优成功。si为算法第i次搜索到的最优值，ξ为给定的阀值。定义寻优成功率η=寻优成功的次数/总寻优次数，BA和EDBA程序分别运行20次，对结果进行统计分析。

文献[14]中的计算结果为1.557，对应的失效概率为5.97%，EDBA和基本BA的计算结果与其基本一致，蒙特卡洛计算10万的失效概率为6.01%。表明了EDBA的准确性，可以作为可靠度计算的一种有效方法；从图2可以看出，EDBA较基本BA的收敛速度快，计算精度比基本BA高；表3中计算统计结果表明：EDBA较基本BA的稳定性更好，搜索效率更高。

表3　BA和EDBA的计算结果统计

EDBA控制参数的不同选取，直接对方法的性能产生较大影响，控制参数主要包括最大进化代数和音量衰减系数、搜索频率的增强系数、固定迁徙概率和当前最优解权值。下面讨论各控制参数对可靠度计算值的影响规律。由于方法具有一定的随机性，为了减小随机性导致的计算结果误差，在同样的参数情况下，程序均运行50次，以平均值作为衡量依据。

5.2EDBA主要控制参数的讨论

为了分析EDBA中各主要控制参数对计算结果的影响，本文采用正交试验对其进行极差分析和方差分析。下文主要对进化代数iterMax、音量的衰减系数(α)、搜索频率的增强系数(γ)、固定迁徙概率(Ped)和当前最优解权值(ω1)5个指标进行分析。这里只考虑当前最优值权重(ω1)，因为ω1+ω2=1。各控制参数分别设置：(500，1 000，2 000)，(0.1，0.5，0.9)，(0.1，0.5，0.9)，(0.1，0.3，0.5)，(0.5，0.7，0.9)。每组数据各运行50次，ζ值取2%，统计其寻优成功率。正交试验计算结果见表4，极差分析结果见表5，方差分析结果见表6。

表4　正交试验结果

从表5和表6中可以看出，EDBA中，对于平均最优值来说，音量衰减系数(α)对计算结果影响最大且灵敏性最高，其F值大于F0.05，说明音量衰减系数对计算结果影响显著；其他四个控制参数的F值均小于F0.05，表明其对计算结果的影响不显著，有利于参数取值。从表6可以得到，最大进化代数(iterMax)各个水平的平均最优值比较接近，说明EDBA的搜索速度较快，当进化代数大于500时，进化代数对计算结果影响较小。最大进化代数为500时的最优值优于进化代数为2 000时的最优值，这主要是由算法随机性误差引起的，当某参数对计算结果影响较小时，相对放大了随机性误差对计算结果的影响，综合考虑进化迭代时间，算法最大进化代数通常设置为1 000。对于算法的寻优成功率，这里以搜索到的最优值1.551为标准，阀值ξ取2%,，从表6中可以看出，固定迁徙概率Ped的F值大于F0.05，表明其对寻优成功率影响显著，增强了算法的全局搜索能力且算法的稳定性更好。音量衰减系数α的F值同样大于F0.05，表明其对寻优成功率的影响同样显著，其余依次为γ，ω1，iterMax，后三位参数在取值时，其约束条件相对宽松，便于参数取值。综合以上分析，EDBA的主要控制参数的最佳取值组合应为(1 000，0.9，0.9，0.3，0.9)。

表5　正交试验极差分析结果

*括号内为分析寻优成功率时的数据

表6　正交试验方差分析结果

*括号内为分析寻优成功率时的数据

由于正交试验法中，各参数的水平数选取有限，下面重点分析固定迁徙概率、音量的衰减系数(α)、搜索频率的增强系数(γ)的具体取值。由表5和表6可得，分析“固定迁徙概率”时，音量的衰减系数(α)、搜索频率的增强系数(γ)均取0.9，其他参数分别取最佳组合值。同样参数设置下，程序运行10次，取可靠度值的平均值作为评价标准。

由图3可见，当固定迁徙概率从0.1～0.3逐渐增大时，可靠度值逐渐减小，但非常接近；当固定迁徙概率从0.3～0.9逐渐增大时，可靠度值逐渐增大；当可靠度值取0.3时，可靠度值最小，表明EDBA的全局搜索能力最强。从整个趋势图分析，可靠度值随着迁徙概率的增大而逐渐增大，主要原因为：当固定迁徙概率大于0.4时，由于迁徙概率过高，导致原优秀蝙蝠个体的特性发生改变，造成解的退化，降低了方法的全局搜索能力。当固定迁徙概率取0.1～0.3时，EDBA的搜索结果非常接近，由于算法具有一定的随机性，因此0.1，0.2，0.3均可作为固定迁徙概率的取值。通常情况下，固定迁徙概率取0.3。

图3　固定迁徙概率对计算结果的影响

下面分析音量衰减系数(α)、搜索频率增强系数(γ)的具体取值，其中固定迁徙概率取0.3，分析‘音量衰减系数’时，搜索频率增强系数取0.9；分析‘搜索频率增强系数’时，音量衰减系数取0.9。

从图4可以看出，随着音量衰减系数和搜索频率增强系数的不断增大，可靠度逐渐减小，表明算法的全局搜索能力得到提高。音量衰减系数当音量衰减系数取0.9时，优化结果最优。搜索频率增强系数取0.4～0.9时，计算结果非常接近，取0.9时结果最优。从二者的趋势图可以看出，音量衰减系数对计算结果的影响较搜索频率大，其取值应慎重。通常情况下，音量衰减系数和搜索频率增强系数均取0.9。

图4　音量衰减系数和搜索频率增强系数对计算结果的影响

由于EDBA在相同种群规模，不同进化代数的情况下，搜索的全局最优解不同，因此进一步分析了“进化代数”与“种群规模”的相互关系及其对EDBA优化结果的影响，本文分别设定进化代数为200，500，1 000，2 000，统计不同种群规模对应的最优结果，其他参数采用最优组合值，同样参数设置下，程序均运行10次，以平均值作为评价标准，统计结果见图5。

图5　种群规模对计算结果的影响

由图5可以得出，当进化代数一定时，随着种群规模的增加，可靠度值不断减小，表明EDBA的全局搜索能力提高。当种群规模取10，20时，进化代数2 000的收敛精度明显优于进化代数200，500，1 000时的收敛精度。当种群规模大于40时，进化代数500，1 000，2 000的收敛精度非常接近。当种群规模大于80时，不同进化代数的收敛精度均十分接近，表明当种群规模达到一定程度时，算法的收敛精度与种群规模大小无明显关系。

综合表5、表6、图3、图4和图5分析，EDBA主要参数(最大进化代数，种群规模、音量衰减系数、搜索频率增强系数、固定迁徙概率)的最优组合取值为(1 000，40，0.9，0.9，0.3)。

5.3算例2：Cannon坝

众多学者对加拿大的Cannon坝的坝体稳定性问题进行了研究[16]，断面见图6，表7所示为各土层参数，其中黏土层Ⅰ、Ⅱ的粘聚力c和内摩擦角φ视为随机变量，服从对数正态分布，见表8。

假定坝体在土层自重作用下发生破坏，随机变量取均值，其他参数见表7，采用Bishop法计算坝体的安全系数为2.49。

图6　Cannon 坝剖面图

土层粘聚力c/kPa内摩擦角φ/(°)重度/(kN/m3)黏土层Ⅰ/Ⅱ22滤砂器53522砂基础51820填土53525石灰岩2504626

表8　黏土层Ⅰ、Ⅱ的参数

该算例中，坝体的安全系数没有显示的功能函数，需要通过数值软件进行计算。在第一次迭代中，采用均匀设计法在[-3σ，3σ]选取15个样本点。在后续迭代中，为了提高拟合精度，分别在[-σ，σ]和[-0.5σ，0.5σ]选取，GEP方法参数设置见表9，计算结果见表10。

表9　GEP方法参数设置表

表10　各方法计算边坡可靠度结果对比

由表10可以看出，EDBA-GEP方法计算得到的可靠度指标与ANN法的计算结果接近，误差为2.63%，在允许的误差范围之内；与SVM的误差为6.97%，产生误差的原因有：①计算安全系数所采用的方法不同；②计算可靠度的方法不同；③计算的模型尺寸略有差异。但对于边坡工程来说，这样的误差均在允许范围之内。

为检验GEP方法对功能函数的拟合精度，在[-3σ，3σ]随机取出20组数据，利用GEP方法在第一次迭代中拟合的函数，对这20组数据进行预测，并与计算值进行比较，结果见图7。从图7可以看出，在[-3σ，3σ]范围内，GEP方法的预测值较为精确，预测值较计算值的误差均在8%以内，最低0.79%；以验算点为中心，[-0.5σ，0.5σ]范围内随机取出20组数据，利用GEP方法在最后一次迭代中的拟合函数进行预测，并与计算值进行对比，见图8。从图8可以看出，在验算点附近，GEP方法的拟合精度较[-3σ，3σ]内有明显提高，与计算值的误差均在1%以内。

图7　GEP方法在全局范围内的拟合精度

图8　验算点附近GEP方法拟合精度

6结论

(1)借鉴细菌觅食优化算法中的迁徙操作，将其引入基本蝙蝠算法中，当满足操作条件时，随机选择一定数量的个体进行迁徙操作，重新分配到寻优空间中，该方法改善了蝙蝠算法的全局搜索能力，提高了方法的收敛速度、计算精度和稳定性。

(2)利用GEP方法的函数拟合功能，和响应面方法相结合，拟合边坡极限状态曲面，将隐式的功能函数显式化，解决了传统响应面方法可能不收敛的问题。

(3)EDBA-GEP方法结合了EDBA和GEP方法的各自优点，对功能函数为显式和隐式的边坡可靠度计算问题均能很好地解决，为边坡可靠性分析提供了一种新方法。

参考文献:

[1]Hassan A M. Wolff T F. Search algorithm for minimum reliability index of earth slope[J].Journal of Geotechnical and Geoenvironmental Engineering,1999,125(12): 301-308.

[2]Christian J, Ladd C, Baecher G. Reliability applied to slope stability analysis[J]. Journal of Geotechnical Engineering,1994,120(12):2180-2207.

[3]El-ramly H, Morgenstern N R, Cruden D M, Probabilistic slope stability analysis for practical[J].Canadian Geotechnical Engineering,2002,39(3):665-683.

[4]Lv Q, Low B K. Probabilistic analysis of underground rock excavations using response surface method and SORM[J].Computers and Geotechnics,2011,38:1008-1021.

[5]Yang X S，Gandomi A H. Bat algorithm: a novel approach forglobal engineering optimization[J].Engineering Computations， 2012,29(5):464-483.

[6]Ferreira C. Gene Expression Programming: Mathematical modeling by an artificial intelligence[M].Berlin: Springer-Verlag,2006.

[7]Yang X S. A new met heuristic bat-inspired algorithm [C]/ /Nature Inspired Cooperative Strategies for Optimization. Springer,2010: 65-74.

[8]胡洁.细菌觅食优化算法的改进及应用研究[D].武汉：武汉理工大学，2012.

[9]刘成忠，韩俊英.基于细菌迁徙的自适应果蝇算法[J].计算机工程与科学,2014,36(4):690-696.

[10]杨萍，孙延明，刘小龙，等.基于细菌觅食趋化算子的PSO算法[J].计算机应用研究，2012,28(10):3640-3642.

[11]林育梁. 岩土与结构工程中不确定性问题及其分析方法[M].北京：科学出版社，2009.

[12]吕大刚，贾明明，李刚.基于均匀设计响应面法的钢结构抗震可靠度分析[J].哈尔滨工业大学学报,2011,43(4):1-5.

[13]Wang Y. Fang K T. A note on uniform distribution and experimental design[J]. Chinese Science Bulletin,1981,26(6):474-485.

[14]Low B.K.Efficient probabilistic algorithm illustrated for a rock slope[J].Journal of Rock Mechanics and Rock Engineering,2008,41(5):715-734.

[15]贺子光，赵法锁，段钊，等.MPSO-GEP方法在边坡可靠度计算中的应用[J].防灾减灾工程学报,2015,35(4):425-432.

[16]何婷婷,尚岳全,吕庆,等.边坡可靠度分析的支持向量机法[J].岩土力学,2013,34(11):3269-3276.

[17]Cho S E. Probability stability analyses of slopes using the ANN-based response surface[J].Computers and Geotechnics,2009,36(5):787-797.

*收稿日期：2016-01-12修回日期：2016-03-12

基金项目：国家自然科学基金应急管理项目(41440021)；西部矿产资源与地质工程教育部重点实验室开放基金项目(310826151137); 陕西省科技计划项目(s2012sF3082)

第一作者简介：贺子光(1987-)，男，河南焦作人，博士研究生，主要从事岩土工程计算与分析方面的研究.E-mail:hzg198762@163.com

中图分类号：X43；P64；Tu457

文献标志码：A

文章编号：1000-811X(2016)03-0031-09

doi:10.3969/j.issn.1000-811X.2016.03.006

The Application of Bat Algorithm in Analysis of Slope Reliability

HEZiguang1,WUBo1,ZHAOFasuo1,CHENGZhenquan1,WANGBanqiao1andDUANZhao2

(1. College of Geology Engineering and Geomatics, Chang’an University, Xi’an 710054, China;2. College of Geology and Environment, Xi’an University of Science and Technique, Xi’an 710054, China)

Abstract:Based on geometrical character of reliability, we put forward using Bat Algorithm (BA) to calculate reliability of slope. In allusion to premature and low convergence precision of basic bat algorithm, by introducing elimination disperse operation in Bacterial Foraging Optimization Algorithm (BFOA) to the basic Bat Algorithm, it forms a Elimination Dispersal Bat Algorithm (EDBA), which can improve the global searching ability and convergence rate. The first example shows that EDBA has higher precision and fast convergence speed than basic BA and is good to solve the reliability analysis problem with complex, nonlinear performance function. For explicit performance function, this paper presents to use a new method comparing Bat Algorithm (BA) and gene expression programming (GEP) to calculate reliability of slope. It adopts GEP method to fit the limit state function of slope, structuring response surface methodology, and uses BA algorithm to solve reliability index and corresponding design points. Results of the second example show that, this method has good adapt ability to solve the reliability analysis problem with implicit performance function, and it is scientific and feasible and has a good application prospect.

Key words:gene expression programming (GEP); bat algorithm (BA); migration; response surface method (RSM); slope; reliabilit

贺子光，吴博，赵法锁，等. 蝙蝠优化算法在边坡可靠性分析中的应用[J]. 灾害学，2016，31(3)：31-38,53. [HE Ziguang, WU Bo, ZHAO Fasuo, et al.The Application of Bat Algorithm in Analysis of Slope Reliability[J].Journal of Catastrophology，2016，31(3)：31-38,53.]