压强对MgSiP2电子结构和热电性能影响的第一性原理研究
戴 姗,刘运牙,杨振华
(1. 湘潭大学材料科学与工程学院,湘潭411105;2. 低维材料及其应用技术教育部重点实验室,湘潭411105;3. 湘潭大学材料设计及制备技术湖南省重点实验室,湘潭411105)
压强对MgSiP2电子结构和热电性能影响的第一性原理研究
戴姗,刘运牙,杨振华
(1. 湘潭大学材料科学与工程学院,湘潭411105;2. 低维材料及其应用技术教育部重点实验室,湘潭411105;3. 湘潭大学材料设计及制备技术湖南省重点实验室,湘潭411105)
摘要:基于第一性原理,计算了MgSiP2的能带结构,结果显示压强减小了能带带隙值,部分电子有效质量随着压强增大而减小。费米能级附近电子态密度计算结果显示:随着压强的增大,价带顶电子态密度的斜率逐渐减小,而导带底电子态密度的斜率逐渐增加。结合半经典玻耳兹曼理论,分别计算了p型和n型MgSiP2的电导率与弛豫时间的比值、赛贝克系数以及功率因子与弛豫时间的比值。结果发现:压强所致部分电子有效质量的减小,提高了p型和n型MgSiP2的电导率,但在一定程度上降低了MgSiP2的赛贝克系数。在压强作用下,相对于n型MgSiP2,p型MgSiP2的电导率增加幅度更大,补偿了压强所致p型MgSiP2赛贝克系数的降低,提高了p型MgSiP2的功率因子,使其大于n型MgSiP2的对应值。计算结果表明,通过增大压强可以提高p型MgSiP2的热电性能,为实验制备具有良好热电性能MgSiP2提供了指导方案。
关键词:MgSiP2;电子结构;热电性能;第一性原理计算
热电材料作为一种重要的功能材料,对减少环境污染和缓解能源危机具有非常重要的作用。它可将热能直接转换成电能,且不会造成环境污染[1],因此,在能量转换方面具有重要的研究价值和广泛的应用前景。目前,在利用废热、余热等进行热能转换电能方面,热电材料已有初步的应用,如日本建立的500 W垃圾燃烧余热发电示范系统,已取得良好的实际效果[2]。但目前热电材料的热电转换效率还比较低,因此,探索高性能热电材料和提升热电材料的热电性能成为研究者关注的重点[3-4]。
热电材料的热电性能可由无量纲的热电优值ZT来衡量[1,5]:ZT=S2σTκ-1,其中,S表示赛贝克(Seebeck)系数,μV·K-1;σ表示电导率,S·m-1;T表示热力学温度,K;κ表示热导率,W·m-1·K-1。S2σ称为功率因子。因此,提升材料的热电性能,可以通过提高材料的功率因子和降低其热导率来实现。目前,提高材料热电优值常见的方法包括对热电材料进行掺杂[6-7]、纳米化热电材料[8-9]、对热电材料加压[10-14]等。如Polvani等对处于300 K的p型Sb1.5Bi0.5Te3合金施加2 GPa的静水压,获得热电性能ZT>2[15],这说明施加压强可以提高材料热电性能。近年来,黄铜矿体系的热电材料因具有较好的热电性能而引起广泛关注,探索不同种类黄铜矿体系热电性能的研究也逐渐兴起[16-21],但目前对黄铜矿结构材料MgSiP2的热电性能[22-25]研究很少,因此,本文将通过第一性原理研究压强对MgSiP2电子结构的影响,并结合半经典玻耳兹曼理论,研究压强对MgSiP2热电性能的影响,提出增大压强以提高MgSiP2热电性能的方法。
1压强对MgSiP2电子结构的影响
1.1MgSiP2的晶体结构

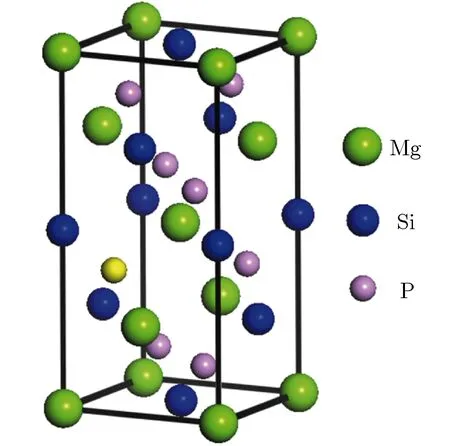
图1MgSiP2晶体结构示意图Fig.1Crystal structure of MgSiP2
1.2MgSiP2的电子结构
首先,对MgSiP2进行结构优化,得到了0,5和10 GPa压强下MgSiP2的晶格常数,如表1所列。从表1可以看出,随着压强的增大,晶格常数a,c逐渐减小,这是由于静水压的作用导致晶体体积变小。表1还给出无压强条件下MgSiP2晶格常数的实验值[10],理论计算值略低于实验值,二者偏差不超过5%,理论计算值与实验值吻合较好。
其次,根据优化后的晶体结构,计算了0, 5 和10 GPa压强下的能带结构,结果如图2所示,其中费米能EF被设置为0。能带计算结果显示,MgSiP2为直接型半导体,压强并未改变MgSiP2直接型半导体这一特性。0 压强下理论计算带隙值比实验带隙值小,是由于GGA通常会低估赝势所致[28-29]。
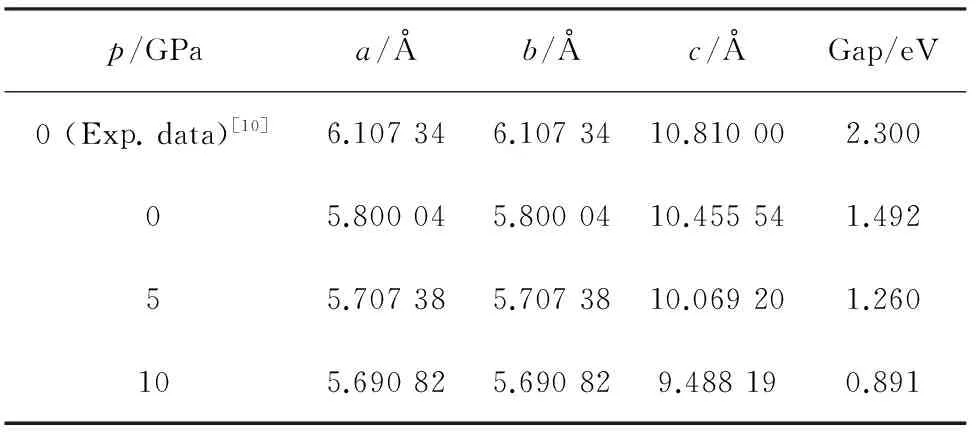
表1 不同压强下MgSiP2的晶格常数与带隙

图2不同压强下MgSiP2的能带结构Fig.2The band structure of MgSiP2under different pressures
从图2可以看出,随着压强的增加,导带底逐渐向费米能靠近,能带斜率增加,能带电子的有效质量减小,这有利于n型MgSiP2电导率的增加。计算结果也显示, 随着压强的增加,价带顶能带变化不明显,但沿Γ至Z方向部分能带斜率增加,能带电子的有效质量减小,这有利于p型MgSiP2电导率的增加。导带底和价带顶部分电子有效质量随着压强的增加而减小,带隙逐渐减小,这表明MgSiP2的电导率将随压强的增加而增加。另外,由于赛贝克系数正比于电子的有效质量[1],因此,电子有效质量的减小也会在一定程度上降低MgSiP2的赛贝克系数。
晶体中电子的态密度与赛贝克系数密切相关。为此,计算了0, 5,10 GPa压强下MgSiP2的电子态密度,结果如图3所示。从图3可以看出,在费米能附近的价带顶处,随着压强的增加,MgSiP2电子态密度的斜率逐渐减小。电子态密度的斜率与赛贝克系数相关,斜率越大,赛贝克系数越大。主要是靠近费米面附近的价带部分决定了p型掺杂半导体的热电性能。在费米能附近导带底处,随着压强的增加,MgSiP2电子态密度的斜率随着压强增大而增大,有利于提高n型MgSiP2赛贝克系数。但图2中导带底电子有效质量随压强增大而减小,又会在一定程度上降低赛贝克系数,因此,MgSiP2赛贝克系数是电子有效质量和电子态密度二者随压强变化总效果的体现。
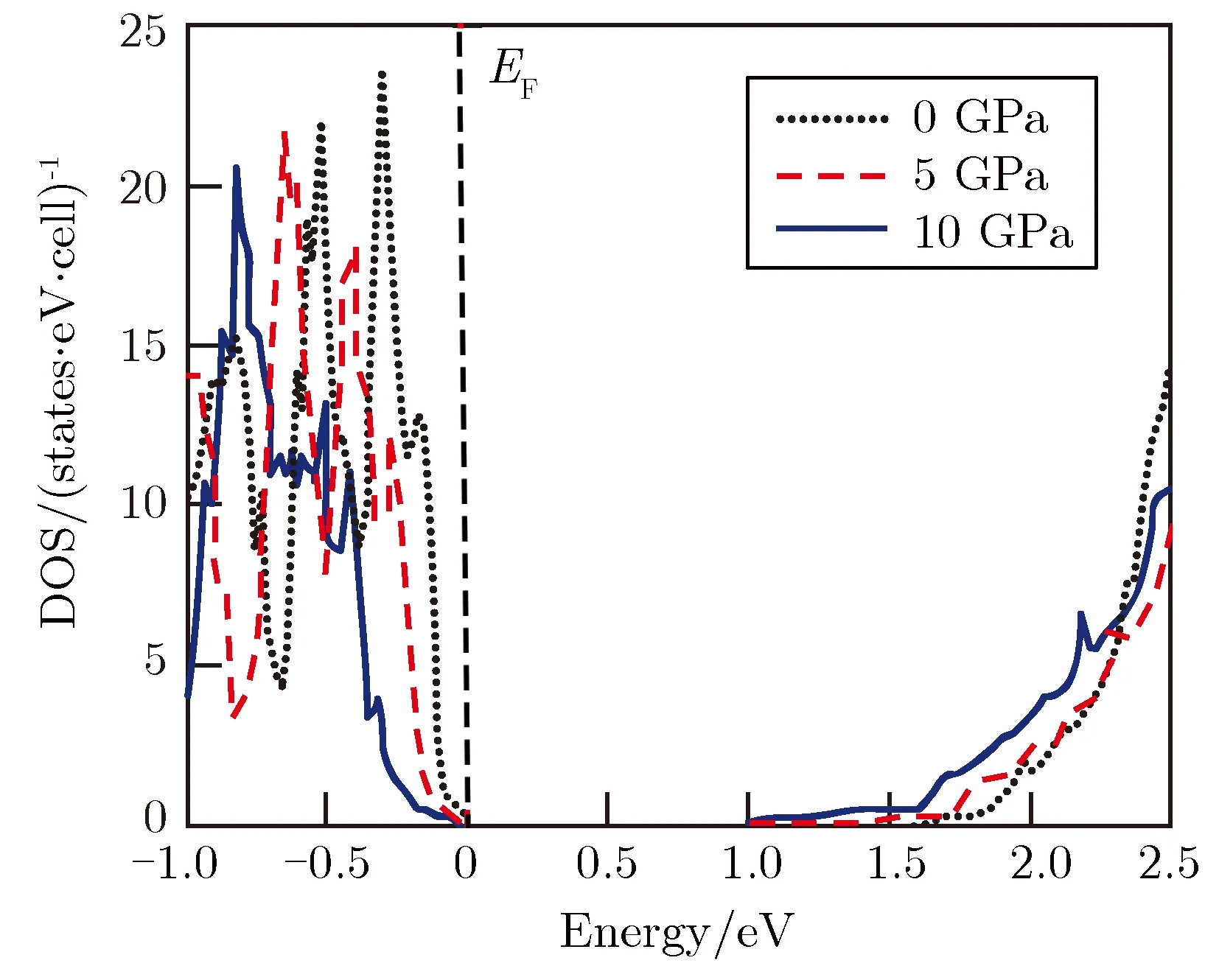
图3不同压强下MgSiP2的电子态密度Fig.3The DOS of MgSiP2 under different pressures
2压强对MgSiP2热电性能的影响
基于半经典玻耳兹曼理论,采用BoltzTraP软件包[30],分别计算并分析了压强对n型和p型MgSiP2热电性能的影响。BoltzTraP软件包建立在半经典玻耳兹曼理论基础上,基于VASP计算得到电子能量本征值、计算材料的电导率和赛贝克系数。本文在计算中采用常弛豫时间近似,这一近似已被广泛地应用于热电性能的计算分析中[31-34]。计算分析了压强对MgSiP2电导率与弛豫时间的比值、赛贝克系数、功率因子与弛豫时间比值的影响。增加载流子浓度可以提高热电材料电导率,但也会降低赛贝克系数,因此,选择合适的载流子浓度才能提升材料的热电功率因子。为此,计算了800 K时无压力条件下MgSiP2的择优载流子浓度,获得了p型掺杂的择优载流子浓度为10.35×1020cm-3,n型掺杂的择优载流子浓度为10.41×1020cm-3。
2.1p型MgSiP2
图4为不同压强下p型MgSiP2热电性能随温度的变化关系。其中图4(a)为电导率与弛豫时间的比值。从图4(a)可以看出,随着温度的增加,不同压强下p型MgSiP2的电导率与弛豫时间的比值均呈现减小的趋势,这是由于通常材料的电导率随温度的升高而降低[35-36]。同时,在同一温度下,由于MgSiP2的带隙逐渐减小,有利于载流子的跃迁,使得p型MgSiP2的电导率与弛豫时间的比值随压强的增加而增大。另一方面,随着压强增大,能带结构中价带顶沿Γ至Z方向部分电子的有效质量减小,增强了电子迁移率[37],提高了p型MgSiP2的电导率。
在图4(b)中,p型MgSiP2的赛贝克系数随温度的增加而增大,但考虑压强时,赛贝克系数随着压强的增加而减小,这与对电子能带结构和电子态密度分析得到预测结果一致。图2中价带顶部分电子有效质量随着压强的增大而减小,虽然提升了p型MgSiP2的电导率,但同时也降低了p型MgSiP2的赛贝克系数。与此同时,图3中电子态密度计算结果显示价带顶处电子态密度斜率随着压强的增大而减小,电子态密度斜率的减小会降低材料的赛贝克系数[38]。因此,压强增加引起价带顶部分电子有效质量的减小以及和电子态密度斜率的降低,同时使p型MgSiP2赛贝克系数的降低,不利于提高p型MgSiP2的赛贝克系数。
基于电导率与弛豫时间的比值以及赛贝克系数的计算结果,在图4(c)中给出不同压强下p型MgSiP2功率因子与弛豫时间比值随温度的变化图。从图4(c)还可以看出, 随着温度的增加,功率因子与弛豫时间的比值逐渐增加。在400~1 000 K范围内,适度增大压强会增强p型MgSiP2的功率因子与弛豫时间的比值,这说明增大压强可提升中高温条件下p型MgSiP2的功率因子,有利于增强p型MgSiP2的热电性能。
2.2n型MgSiP2
计算了不同压强下n型MgSiP2的热电性能随温度的变化,如图5所示。图5(a)是不同压强下n型MgSiP2电导率与弛豫时间的比值随温度的变化关系,结果显示在大部分温度范围内,电导率与弛豫时间的比值随温度的增加而缓慢减小,随着压强的增加而增大,这是由于压强使得导带底电子有效质量减小,增强了载流子的迁移率,从而提高了n型MgSiP2的电导率,这与图2能带结构分析所预测的电导率升高保持一致。
图5(b)给出了不同压强下n型MgSiP2赛贝克系数随温度的变化。由于n型半导体的赛贝克系数为负,所以分析其绝对值随压强的变化。图5(b)表明,大部分温度范围内赛贝克系数绝对值随温度的升高而增加;在300~1 000 K内,赛贝克系数的绝对值都随压强的增加而减小。尽管电子在导带底附近电子态密度的斜率随压强的增大而增大(如图3所示),这种变化有利于n型MgSiP2赛贝克系数的提高,但是在导带底附近电子有效质量的减小(如图2所示)又使得赛贝克系数减小,而且电子有效质量的减小对赛贝克系数的贡献占据了主要部分,从而n型MgSiP2赛贝克系数的绝对值表现为随着压强的增大而减小。
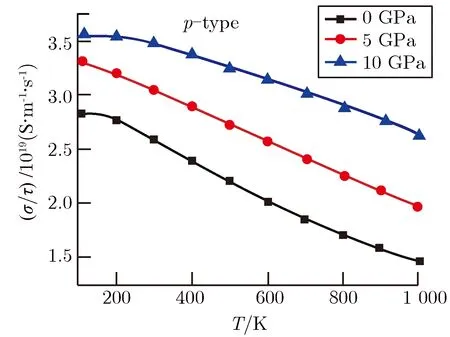
(a)Conductivity divided by relaxation time
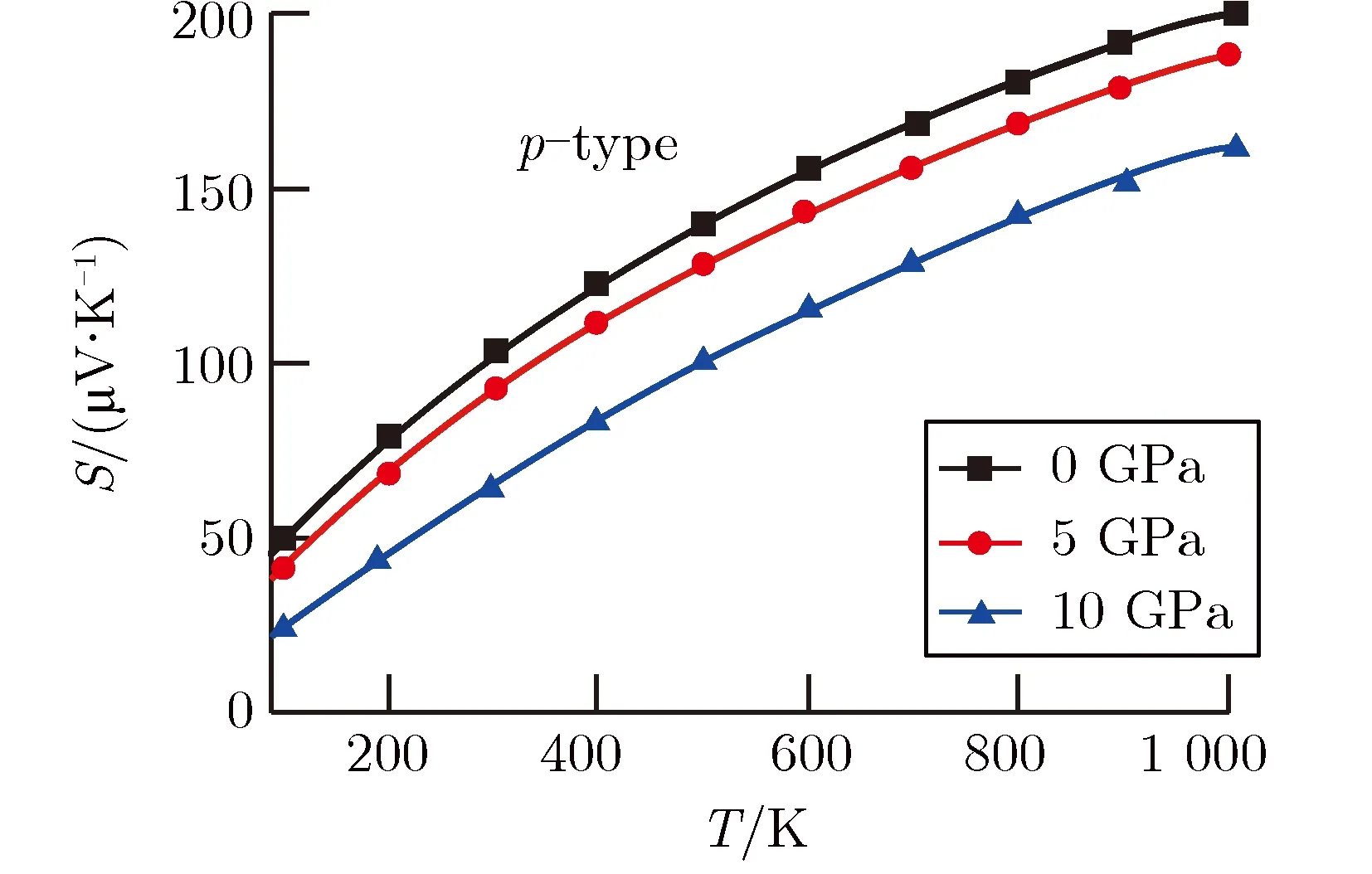
(b)Seebeck coefficient

(c)Power factor divided by relaxation time
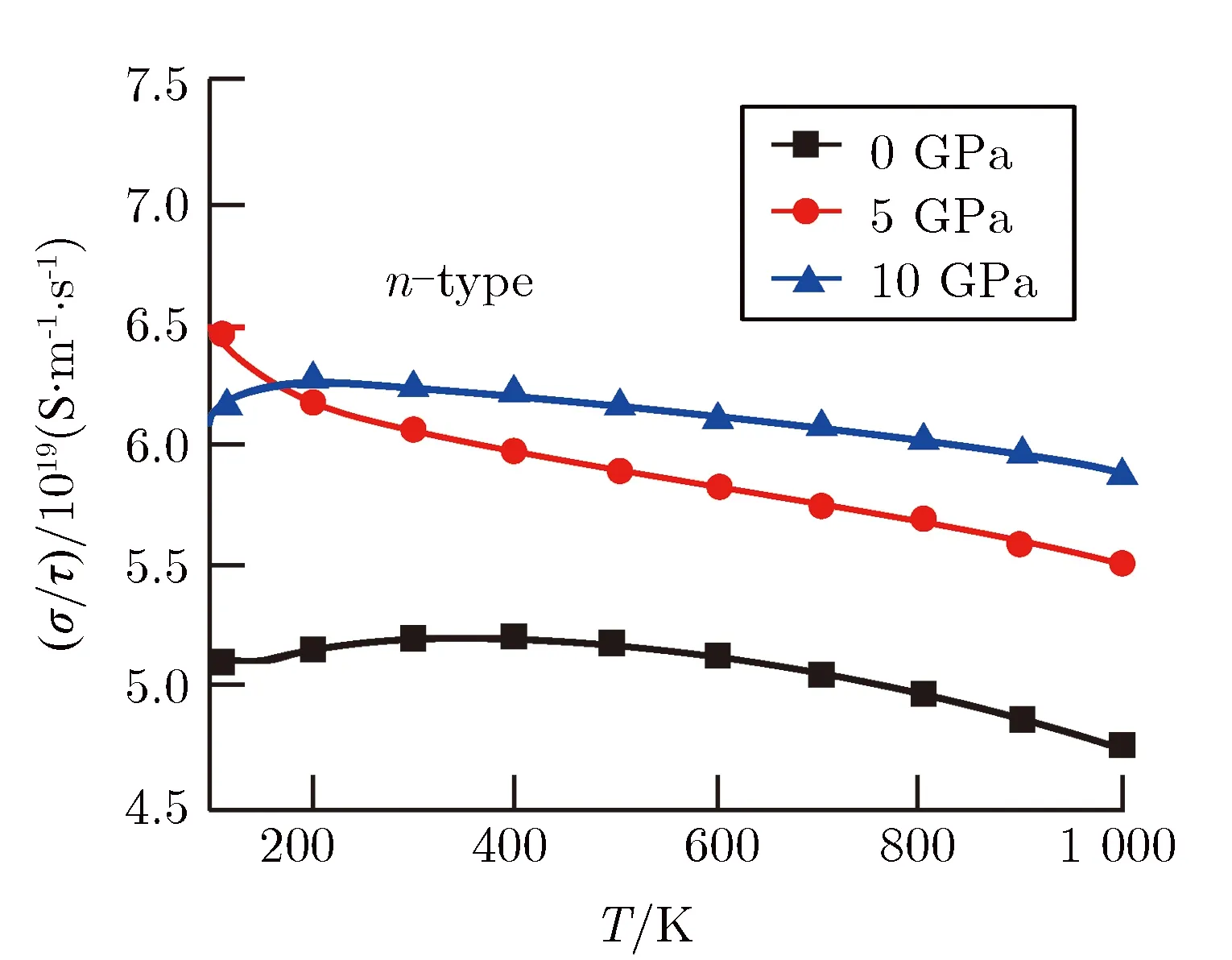
(a)Conductivity divided by relaxation time

(b)Seebeck coefficient

(c)Power factor divided by relaxation time
图5不同压强下n型MgSiP2热电性能随温度的变化
Fig.5Thermoelectric properties ofn-type MgSiP2vs. temperature under different pressures
基于n型MgSiP2的电导率与弛豫时间的比值以及赛贝克系数,计算了n型MgSiP2功率因子与弛豫时间比值随温度的变化,结果如图5(c)所示。功率因子与弛豫时间比值随着温度的升高而增加,增加压强只有在较低温度范围内能够提高n型MgSiP2的功率因子,绝大部分温度范围内,增加压强会降低n型MgSiP2的功率因子,这说明增加压强不利于提高n型MgSiP2的功率因子。
3结论
本文利用第一性原理并结合半经典玻耳兹曼理论,研究了压强对MgSiP2的电子结构和热电性能的影响。能带结构计算结果显示,不同压强下的MgSiP2都表现为直接型半导体,随着压强的增加,带隙值逐渐减小且价带顶和导带底部分电子的有效质量减小,这促进了p型和n型MgSiP2电导率与弛豫时间比值的增加。从电子态密度结果中可以看出,在费米能附近的价带顶处,随着压强的增加,MgSiP2电子态密度的斜率逐渐减小,结合价带顶部分电子有效质量的减小,说明p型MgSiP2的赛贝克系数随着压强的增加而减小。同时,导带底电子有效质量的减小,也使得p型MgSiP2的赛贝克系数随着压强的增加而减小。相对于n型MgSiP2,增加压强使p型MgSiP2的电导率增加幅度更大,补偿了压强所致p型MgSiP2赛贝克系数的降低,因此压强能够增强p型MgSiP2的功率因子,且p型MgSiP2的热电性能优于n型MgSiP2的热电性能。这表明,压强能够使得p型MgSiP2表现出较高的热电转换效率,为实验上制备优异热电性能的MgSiP2材料提供了良好的指导方案。
参考文献
[1]HEREMANS J P, JOVOVIC V, TOBERER E S, et al. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states[J]. Science, 2008, 321(5 888): 554-557.
[2]李洪涛,朱志秀,吴益文,等. 热电材料的应用和研究进展 [J].材料导报, 2012, 26(15): 57-61. (LI Hong-tao, ZHU Zhi-xiu, WU Yi-wen, et al. Progress of application and research of thermoelectric materials [J]. Materials Review, 2012, 26(15): 57-61.)
[3]RHYEE J S, LEE K H, LEE S M, et al. Peierls distortion as a route to high thermoelectric performance in In4Se3-δcrystals[J]. Nature, 2009, 459(7 249): 965-968.
[4]SHAKOURI A. Recent developments in semiconductor thermoelectric physics and materials[J]. Annual Review of Materials Research, 2011, 41: 399-431.
[5]PEI Y E, SHI X Y, LALONDE A, et al. Convergence of electronic bands for high performance bulk thermoelectrics[J]. Nature, 2011, 473(7345): 66-69.
[6]LIU W, TAN X J, YIN K, et al. Convergence of conduction bands as a means of enhancing thermoelectric performance ofn-type Mg2Si1-xSnxsolid solutions[J]. Phys Rev Lett, 2012, 108(16): 166601.
[7]KUO J H, ANDERSON H U, SPARLIN D M. Oxidation-reduction behavior of undoped and Sr-doped LaMnO3: Defect structure, electrical conductivity, and thermoelectric power[J]. Journal of Solid State Chemistry, 1990, 87(1): 55-63.
[8]PICHANUSAKORN P, BANDARU P. Nanostructured thermoelectrics[J]. Materials Science and Engineering, R: Reports, 2010, 67(2): 19-63.
[9]PEI Y E, LENSCH F J, TOBERER E S, et al. High thermoelectric performance in PbTe due to large nanoscale Ag2Te precipitates and La doping[J]. Advanced Functional Materials, 2011, 21(2): 241-249.
[10]OUAHRANI T. Chemical and physical insight on the local properties of the phosphides XSiP2(X= Be, Mg, Cd, Zn and Hg) under pressure: from first principles calculations[J]. The European Physical Journal B, 2013, 86(9): 1-11.
[11]MENG J F, POLVANI D A, JONES C D W, et al. Pressure tuning in the chemical search for improved thermoelectric materials: NdxCe3-xPt3Sb4[J]. Chem Mater, 2000, 12(1): 197-201.
[12]SU T C, JIA X P, MA H A, et al. Enhanced thermoelectric performance of AgSbTe2synthesized by high pressure and high temperature[J]. Appl Phys, 2009, 105(7): 073713.
[13]OVSYANNIKOV S V, SHCHENNIKOV V V, VORONTSOV G V, et al. Giant improvement of thermoelectric power factor of Bi2Te3under pressure[J]. J Appl Phys, 2008, 104(5): 053713.
[14]CHEN F, STOKES K L, NOLAS G S. Thermoelectric properties of tin clathrates under hydrostatic pressure[J]. Journal of Physics and Chemistry of Solids, 2002, 63(5): 827-832.
[15]POLVANI D A, MENG J F, CHANDRA SHEKAR N V, et al. Large improvement in thermoelectric properties in pressure-tunedp-type Sb1.5Bi0.5Te3[J]. Chem Mater, 2001, 13(6): 2 068-2 071.
[16]WU W J, WU K C, MA Z J, et al. Doping and temperature dependence of thermoelectric properties of AgGaTe2: First principles investigations[J]. Chem Phys Lett, 2012, 537: 62-64.
[17]LIU R H, XI L L, LIU H L, et al. Ternary compound CuInTe2: a promising thermoelectric material with diamond-like structure[J]. Chem Commun, 2012, 48(32): 3 818-3 820.
[18]YAO J L, TAKAS N J, SCHLIEFERT M L, et al. Thermoelectric properties ofp-type CuInSe2chalcopyrites enhanced by introduction of manganese[J]. Phys Rev B, 2011, 84(7): 075203.
[19]LI Y P, MENG Q S, DENG Y, et al. High thermoelectric performance of solid solutions CuGa1-xInxTe2(x= 0-1.0)[J]. Appl Phys Lett, 2012, 100(23): 231903.
[20]KOSUGA A, PLIRDPRING T, HIGASHINE R, et al. High-temperature thermoelectric properties of Cu1-xInTe2with a chalcopyrite structure[J]. Appl Phys Lett, 2012, 100(4): 042108.
[21]ZOU D F, XIE S H, LIU Y Y, et al. First-principles study of thermoelectric and lattice vibrational properties of chalcopyrite CuGaTe2[J]. Journal of Alloys and Compounds, 2013, 570: 150-155.
[22]PETUKHOV A G, LAMBRECHT W R L, SEGALL B. Electronic structure of wide-band-gap ternary pnictides with the chalcopyrite structure [J]. Phys Rev B, 1994, 49(7): 4 549-4 558.
[23]POPLAVNOI A S, POLYGALOV Y I, CHALDYSHEV V A. Energy-band structure of semiconductors having the chalcopyrite lattice II. MgSiP2, ZnGeP2, ZnSiAs2, and CdSiP2[J]. Soviet Physics Journal, 1970, 13(6): 766-770.
[24]JAFFE J E, ZUNGER A. Electronic structure of the ternary pnictide semiconductors ZnSiP2, ZnGeP2, ZnSnP2, ZnSiAs2, and MgSiP2[J]. Phys Rev B, 1984, 30(2): 741-756.
[25]SHI L, HU J, QIN Y, et al. First-principles study of structural, elastic and lattice dynamical properties of chalcopyrite BeSiV2and MgSiV2(V= P, As, Sb)[J]. Journal of Alloys and Compounds, 2014, 611: 210-218.
[26]KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals[J]. Phys Rev B, 1993, 47(1): 558-561.
[27]KRESSE G, FURTHMULLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set [J]. Computational Materials Science, 1996, 6(1): 15-50.
[28]MORI-SANCHEZ P, COHEN A J, YANG W. Localization and delocalization errors in density functional theory and implications for band-gap prediction[J]. Phys Rev, 2008, 100(14): 146401.
[29]OBUKURO Y, MATSUSHIMA S, OBATA K, et al. Improved calculation of band gap of Sr2Bi2O5crystal using modified Becke-Johnson exchange potential [J]. Journal of Physics and Chemistry of Solids, 2014, 75(3): 427-432.
[30]MADSEN G K H, SINGH D J. BoltzTraP: A code for calculating band-structure dependent quantities[J]. Computer Physics Communications, 2006, 175(1): 67-71.
[31]PARKER D, SINGH D J. Thermoelectric properties of AgGaTe2and related chalcopyrite structure materials[J]. Phys Rev B, 2012, 85(12): 125209.
[32]SINGH D J, MAZIN I I. Calculated thermoelectric properties of La-filled skutterudites[J]. Phys Rev B, 1997, 56(4): 1 650-1 653.
[33]NOUGIER J P, VAISSIERE J C, GASQUET D, et al. Determination of transient regime of hot carriers in semiconductors using the relaxation time approximations[J]. J Appl Phys, 1981, 52(2): 825-832.
[34]ONG K P, SINGH D J, WU P. Analysis of the thermoelectric properties ofn-type ZnO[J]. Phys Rev B, 2011, 83(11): 115110.
[35]BISWAS K, HE J Q, BLUM I D, et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures[J]. Nature, 2012, 489(7 416): 414-418.
[36]ZOU D F, XIE S H, LIU Y Y, et al. Electronic structure and thermoelectric properties of half-Heusler Zr0.5Hf0.5NiSn by first-principles calculations[J]. J Appl Phys, 2013, 113(19): 193705.
[37]YAN Y L, WANG Y X. Crystal structure, electronic structure, and thermoelectric properties of Ca5Al2Sb6[J]. Journal of Materials Chemistry, 2011, 21(33): 12 497-12 502.
[38]ZOU D F, XIE S H, LIU Y Y, et al. Electronic structures and thermoelectric properties of layered BiCuOCh oxychalcogenides (Ch=S, Se and Te): first-principles calculations[J]. J Mater Chem A, 2013, 1(31): 8 888-8 896.
(上接第020403-4页)
[8]梁曦东, 陈昌渔, 周远翔. 高电压工程[M]. 北京: 清华大学出版社, 2003. (LIANG Xi-dong, CHEN Chang-yu, ZHOU Yuan-xiang. High Voltage Engineering[M]. Beijing: Tsinghua University Press, 2003.)
[9]COOPER J R, HUTCHESON G, KRISTIANSEN M, et al. A multi-spark preionization source for diffuse discharges containing attachers [C]//IEEE 4th International Pulsed Power Conference, 1983: 726-728.
[10]邵涛, 孙广生, 严萍,等. 高压纳秒脉冲气体放电试验研究进展[J].高压电器,2004,40(4): 279-282. (SHAO Tao, SUN Guang-sheng, YAN Ping, et al. Progress in the experiment and research of gas breakdown under HV nanosecond pulse[J]. High Voltage Apparatus, 2004, 40(4): 279-282.)
[11]严璋, 朱德恒. 高电压绝缘技术[M]. 北京: 中国电力出版社,2007. (YAN Zhang, ZHU De-heng. High Voltage and Insulation Technology[M]. Beijing: China Electric Power Press, 2007.)
[12]MARTIN T H. Pulsed charged gas breakdown [C]//5th IEEE Pulsed Power Conference, 1985, 74-83.
(上接第020601-4页)
[10]藤井信生. 运算放大器的基础与应用[M]. 赵满良, 彭连昌, 译. 北京: 电子工业出版社, 1983.(FUJII NOBUK. Basis and Application of Operational Amplifier [M]. (ZHAO Man-liang, PENG Lian-chang, translated. Beijing: Publishing House of Electronics Industry, 1980.)
[11]颉晓明. 集成运算放大器的失效分析及防护[J]. 河南科学, 2009, 27(10): 1 254-1 257.(XIE Xiao-ming. Integration operational amplifier’s failure analysis and protection[J]. Henan Science, 2009, 27(10): 1 254-1 257.)
[12]鲍秀峰. 军用集成电路典型失效模式分析与改进措施研究[D]. 南京: 南京理工大学, 2006.(BAO Xiu-feng. Research on typic failure model and improvement measure of military integrated circuits[D]. Nanjing: Nanjing University of Science & Technology, 2006.)
[13]王长河. 高功率微波和电磁脉冲对半导体器件辐射损伤的研究[J]. 半导体情报, 1997, 34(1): 9-16.(WANG Chang-he. Study on the effect of HPM and EMP radiation damage on semiconductor devices[J]. Semiconductor Information, 1997, 34(1): 9-16.)
收稿日期:2015-06-12;修回日期:2016-01-26
作者简介:戴姗(1990- ),女,湖北天门人,硕士研究生,主要从事新型能源材料研究。 E-mail:Dshan33@aliyun.com
中图分类号:TN377
文献标志码:A
文章编号:2095-6223(2016)020801(7)
The Effects of Pressure on Electronic Structures and Thermoelectric Properties of MgSiP2by First-Principles Calculations
DAIShan,LIU Yun-ya,YANG Zhen-hua
(1. School of Materials Science and Engineering, Xiangtan University,Xiangtan411105,China;2. Key Laboratory of Low Dimensional Materials and Application Technology of Ministry of Education, Xiangtan411105,China;3. Key Laboratory of Materials Design and Preparation Technology of Hunan Province, Xiangtan University,Xiangtan411105,China)
Abstract:The band structures of MgSiP2 under different pressures were investigated by using first-principles calculations. It was found that the band gap and some of electron effective mass of MgSiP2 decrease with the increase of pressure. The results of the density of electronic state (DOS) near the Fermi level show that the slope of DOS decreases with the increases of pressure at the top of valence band, while it shows a contrary trend at the bottom of conduction band. The thermoelectric properties of p-type and n-type MgSiP2 were calculated using the semi-classical Boltzmann transport theory. The results show that both the electric conductivities of p-type and n-type MgSiP2 increase with respect to pressure, while the Seebeck coefficients decrease with respect to pressure due to the decrease of electron effective mass. Although the Seebeck coefficients decrease under pressure, the enhancement of electric conductivity of p-type is more obvious than that of n-type MgSiP2, resulting in the enhancement of power factor of p-type MgSiP2 under pressure. The power factor of p-type MgSiP2 is higher than that of n-type MgSiP2. These insights point to alternative pathways to enhance the thermoelectric properties of MgSiP2 materials.
Key words:MgSiP2;electronic structure;thermoelectric properties;first-principles calculations

