基于消隐记忆SCKF的交互式多模型算法

刘鹏远,吴　博

(解放军军械工程学院，河北 石家庄 050003)



基于消隐记忆SCKF的交互式多模型算法

刘鹏远,吴博

(解放军军械工程学院，河北 石家庄 050003)

摘要:针对交互式多模型算法(Interacting Multiple Model，IMM)在机动目标跟踪时，因模型不准确导致的滤波误差增大问题，提出了基于消隐记忆平方根容积卡尔曼滤波(Memory Attenuation Square Root Kalman Filter，MASCKF)的交互式多模型算法(IMM-MASCKF)。该算法在模型滤波中引入消隐记忆滤波理论，通过消隐记忆因子增大新息在滤波中的比重，改善了滤波器对目标机动的动态性能，提高了滤波精度。仿真结果表明，该算法可以实现对机动目标的有效跟踪，且与常规交互式多模型算法相比减小了滤波误差。

关键词:机动目标跟踪；交互式多模型；平方根滤波；容积卡尔曼滤波；消隐记忆滤波

0引言

由于空中目标机动能力的不断提升，目标跟踪尤其是对目标机动的跟踪一直是滤波理论的研究热点。要实现高精度的滤波，首先要有足够多能够准确描述目标运动的模型，所以单模型滤波器很难满足机动目标的滤波精度要求。交互式多模型方法是一种次优的滤波算法，其利用多个不同目标模型的子滤波器并行滤波，对其输入和输出加权作为整个滤波器的输入和输出。交互式多模型算法实现了各个子滤波器动态性能和稳态性能的折中。其滤波的精度受制于选取的子滤波器性能和发生机动时模型转移的速度两个因素[1]。

提高模型转移速度的方法主要集中在实现模型概率矩阵的自适应[2-3]。在交互式多模型算法中常用的非线性子滤波器有扩展卡尔曼滤波、无迹卡尔曼滤波、容积卡尔曼滤波、粒子滤波等。交互式多模型算法在跟踪机动目标时因模型不准确而出现滤波误差增大问题，本文针对此问题，提出了基于MASCKF的交互式多模型算法。

1线性简化IMM-SCKF算法

1.1SCKF算法原理

SCKF算法是在容积卡尔曼滤波算法的基础上，结合平方根滤波理论得到的一种算法[4-5]。SCKF算法避免了矩阵分解和求逆运算，拥有更好的数字稳定性。

在双坐标体制雷达系统中，其状态方程通常是线性的。根据文献[6]，当系统方程为线性方程时，SCKF的时间更新过程可以进行线性化简化。设系统转移矩阵为Φ，则线性化后的SCKF算法时间更新过程为：

时间更新：

田志芳这一路不是睡轮船火车卡车，就是帐篷，哪见过这玩意儿。半信半疑地走下去，见平地挖出一个四方地坑，有“门”无窗，除了一块土基高至膝盖，啥都没有。那土台上垫有胡麻草和芨芨草，她的行李已放在上面，田志芳猜想，这就是床。地坑顶上铺着厚厚的红柳枝和杨树枝，上面糊着泥巴，最外层铺着与地面一样的沙土。

P(k-1)=S(k-1)ST(k-1)

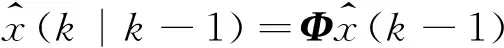
量测更新：

Sy(k)=Tria([γ(k),SR(k)]T)

其中：

Pxy(k)=χ(k)γT(k)

估计滤波增益及k+1时刻状态：

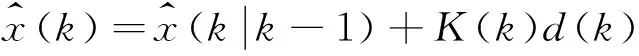
1.2IMM-SCKF算法

IMM算法是一种费效比较高的机动目标跟踪算法。IMM-SCKF算法使用多个SCKF子滤波器并行工作，子滤波器间以Markov概率转移矩阵进行软切换，滤波器的输出状态估计是各子滤波器状态估计融合的结果[7]。一个完整的IMM-SCKF算法循环由四部分组成：输入交互、子滤波器滤波、模型概率更新、输出融合[2]。

1.2.1输入交互

计算子滤波器混合概率：

其中,pij是Markov概率转移矩阵，cj是归一化常数，其计算式如下：

计算混合状态输入：

1.2.2子滤波器滤波

利用第一步得到的状态输入和上一小节的简化SCKF算法进行滤波，得到每一个子滤波器的状态估计和对应的协方差矩阵。

1.2.3模型概率更新

计算各模型似然函数:

根据文献[8]，在SCKF算法中，滤波信息vj(k)及其协方差Sj(k)可以表示为：

计算模型概率：

1.2.4输出融合

一步预测输出融合：

2基于MASCKF的IMM算法

2.1MASCKF算法

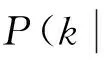
图1展示了加入消隐记忆因子λ前后，滤波增益矩阵K中第一行第二列元素K(1,2)在滤波过程中的变化。

图1　K(1,2)变化曲线Fig.1　Curve of K(1,2)

从上图中可以看出，加入消隐记忆因子后，在MASCKF算法中，K(1,2)要比在SCKF算法中的取值大20%左右，滤波新息在滤波估计中的权重得到了提高。

2.2基于MASCKF的IMM算法设计

为实现对机动目标的良好跟踪，设计了包含两个子滤波器的IMM算法。其中选择常速模型(Constant Velocity Model，CV)作为第一个子滤波器的模型，构成CV-SCKF算法，用于跟踪目标的匀速运动。选择当前统计模型(Current Statistical Model, CS)[10]作为第二个子滤波器的目标运动模型。根据上文描述，为了提高滤波器对目标机动的响应速度，在第二个子滤波器中引入消隐记忆因子，构成CS-MASCKF算法用于跟踪目标机动。两个子滤波器融合交互构成了基于MASCKF的IMM算法，其算法流程如图2所示。

图2　IMM-MASCKF算法流程Fig.2　Flow chart of IMM-MASCKF

3仿真分析

为了检验新算法在机动目标的状态跟踪性能上是否得到改善，进行了跟踪机动目标的仿真实验，并与常规IMM-SCKF算法以及两个子滤波器CV-SCKF和CS-MASCKF算法的跟踪结果进行了比较，验证了新算法的有效性。

定义对目标跟踪的位置均方根误差(Root Mean Square Error，RMSE)如下：

定义x轴上的速度、量测角度、量测距离以及位置上的平均均方根误差(AverageRootMeanSquareError，ARMSE)和位置上的最大均方根误差(MaximumRootMeanSquareError，MRMSE)如下：

仿真实验条件：观测站固定于原点，起始位置和速度分别为(20，20)km和(-100，-100)m/s，目标在x方向上0～50 s做匀速直线运动，第50～80 s做加速度为-4g的加速机动，80～125 s做匀速直线运动。观测角度上的噪声为0.003 rad，观测距离上的噪声为40 m。经过200次的Monte-Carlo仿真，四种算法对加速度的跟踪效果如图3所示。

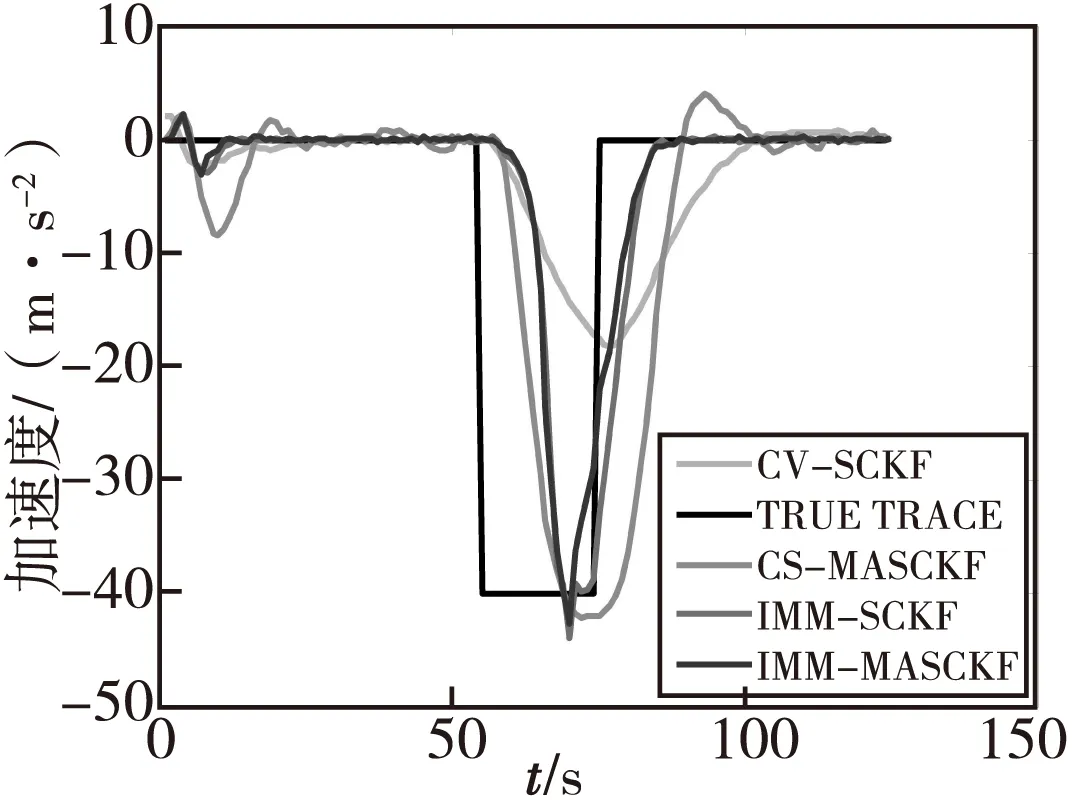
图3　加速度跟踪曲线Fig.3　Tracking curve of acceleration

通过图3中四种算法对加速度的跟踪曲线比较，可以看出CV-SCKF算法对目标机动响应最慢，跟踪误差也最大，但是其稳态跟踪误差最小。CS-MASCKF算法对目标机动响应最快，但是在跟踪加速运动向匀速运动转换过程时，该算法有很大的滞后。两种IMM算法在目标机动初始阶段的响应速度比CS-MASCKF算法略有滞后，但是在机动结束时，IMM算法的响应速度明显比CS-MASCKF算法快，而且在目标匀速运动期间，IMM算法的加速度跟踪误差与CV-SCKF算法相当。

评价目标跟踪滤波器滤波效果时，采用对目标的位置跟踪RMSE作为评价标准。图4展示的是200次Monte-Carlo仿真后四种算法的位置跟踪RMSE比较。

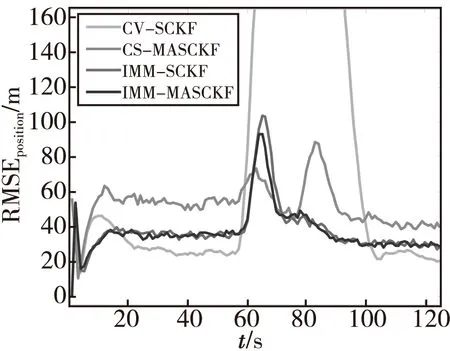
图4　位置跟踪RMSEFig.4　Position tracking RMSE

通过图4可知，CV-SCKF算法对目标匀速运动跟踪效果最好，其位置跟踪RMSE只有CS-MASCKF算法的一半左右，但是CV-SCKF算法在跟踪目标加速机动时位置RMSE急剧增大，远远超过了稳态跟踪RMSE，而CS-MASCKF算法在跟踪目标加速机动时，仅仅出现了两个较小的RMSE尖峰。两种IMM算法对目标匀速运动跟踪RMSE比CV-SCKF算法略大，远小于CS-MASCKF算法，跟踪目标加速机动时，IMM算法出现了一个比CS-MASCKF算法更大的RMSE尖峰，这主要是由于IMM算法的模型转换存在一定延迟造成的，但是由于综合了CV模型的优点，IMM算法在跟踪目标由加速向匀速运动的转换过程时产生的RMSE要小于CS-MASCKF算法。而IMM-MASCKF算法在尖峰处的RMSE比IMM-SCKF算法更小。

上述四种算法的主要性能指标如表1所示。

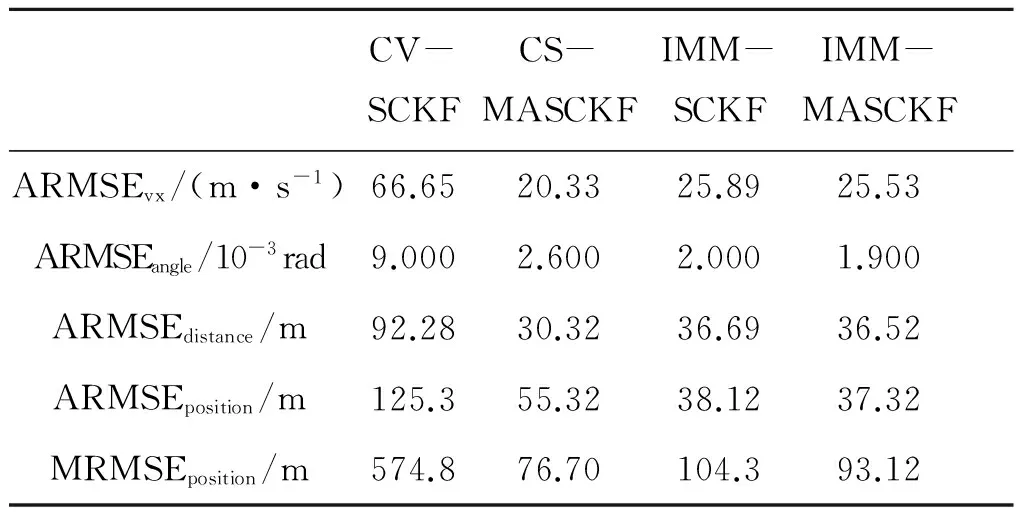
表1　算法滤波效果比较

从表1中的数据对比可知，CV-SCKF算法所有指标都是最差的，这是因为目标的模型不符，造成了巨大的模型误差。CS-MASCKF算法对目标速度跟踪能力最好，其位置RMSE的最值也最小，这是由于加入消隐记忆因子后，CS模型对目标机动的响应更快，能有效抑制RMSE的超调量。IMM算法的角度和位置跟踪效果最好，这是因为IMM算法一定程度上综合了CV模型对目标匀速运动的跟踪能力和CS模型对目标加速的跟踪能力，所以整体上的滤波效果要优于两种子滤波器。IMM-MASCKF算法的性能整体上比IMM-SCKF更优，其中由于消隐记忆因子的引入，IMM-MASCKF算法对目标机动的响应速度更快，使得该算法的RMSE最值比IMM-SCKF算法下降了10.8%，模型误差得到了有效抑制。

4结论

本文提出了基于MASCKF的交互式多模型算法。该算法改善了滤波器的动态性能，提高了滤波器对目标机动的响应速度，同时保留了滤波器良好的稳态跟踪性能，提高了目标跟踪精度。Monte-Carlo仿真结果表明，IMM-MASCKF算法能够实现对目标的有效跟踪，其稳态性能与IMM-SCKF算法相当，但是其动态跟踪能力优于IMM-SCKF算法，是一种有效的机动目标跟踪算法。

通过IMM-MASCKF算法和CS-MASCKF算法的比较可以看出，IMM算法的动态响应速度相较于单模型算法仍然有相当差距，下一步应当着力于进一步提高模型切换速度，从而提高算法的整体滤波性能。

参考文献:

[1]李鸿艳,冯新喜.目标跟踪中的多模型算法发展综述[J].电讯技术，2003(2):12-15.

[2]周卫东,蔡佳楠,孙龙.具有最优模型传递矩阵的交互式多模型算法[J].哈尔滨工业大学学报，2014，46(11):101-106.

[3]封普文,黄长强,曹林平,等.马尔可夫矩阵修正IMM跟踪算法[J].系统工程与电子技术，2013，35(11):2269-2274.

[4]Ienkaran Arasaratnam, Simon Haykin. Cubature Kalman filters[J].IEEE Trans on Automatic Control, 2009, 54(6): 1254-1269.

[5]Ienkaran Arasaratnam, Simon Haykin. Cubature Kalman smoothers [J]. Automatica, 2011, 47: 2245-2250.

[6]戴定成,蔡宗平,牛创.基于简化平方根容积卡尔曼滤波的跟踪算法[J].电光与控制，2015，22(3):11-14.

[7]Blom H A P， Bar-Shalom Y. The interactive multiple model algorithm for system with markov switching coefficients [J]. IEEE Trans. on Automatic Control, 1988, 33(8): 780-783.

[8]郭志,董春云,蔡远利,等.时变转移概率IMM-SRCKF机动目标跟踪算法[J].系统工程与电子技术，2015，37(1):24-30.

[9]蔡佳,黄长强,井会锁,等.基于指数加权的改进衰减记忆自适应滤波算法[J].探测与控制学报，2013，35(4):21-26.

[10]钱华明,陈亮,满国晶,等.基于当前统计模型的机动目标自适应跟踪算法[J].系统工程与电子技术，2011，33(10):2154-2158.

*收稿日期:2016-01-05

作者简介:刘鹏远(1975—),男，河南洛阳人，博士，副教授，研究方向：导弹武器系统建模与仿真。E-mail:bluegd@qq.com。

中图分类号:TP412

文献标志码:A

文章编号：1008-1194(2016)03-0052-05

Interacting Multiple Model Algorithm Based on Memory Attenuation SKCF

LIU Pengyuan, WU Bo

(Ordnance Engineering College, Shijiazhuang050003, China)

Abstract:In order to decrease filtering error caused by inaccurate model when tracking maneuvering target by interacting multiple model(IMM) algorithm, an IMM algorithm based on memory attenuation square root Kalman filter (IMM-MASCKF) was proposed. Attenuation memory filtering theory was applied in the filtering, and the proportion of new measurement in filter was increased through the attenuation memory factor, and then the dynamic performance for maneuvering target tracking and filtering precision was improved. Simulation results showed that the proposed algorithm was effective for maneuvering target tracking, and the filtering error was reduced in comparison with conventional interactive multiple model algorithm.

Key words:maneuvering target tracking; interacting multiple model; square root filtering; cubature Kalman filter; memory attenuation filtering