基于全相位傅里叶变换的多普勒信号频谱提取

雍得鹏，邹金龙，夏　雷，韩银福

(机电动态控制重点实验室，陕西 西安 710065)



基于全相位傅里叶变换的多普勒信号频谱提取

雍得鹏，邹金龙，夏雷，韩银福

(机电动态控制重点实验室，陕西 西安 710065)

摘要:针对截断效应和栅栏效应所带来的频谱泄露的问题，提出基于全相位快速傅里叶变换的多普勒信号频谱提取方法。该方法通过全相位快速傅里叶变换算法实时获取多普勒回波信号的幅度信息，进行幅度和频率的修正。理论和实测的多普勒信号仿真表明，相对于短时傅里叶变换，校正的全相位快速傅里叶变换算法提取的频谱更贴近理想多普勒信号频谱，其频谱幅度信息满足峰值识别的要求。

关键词:引信；调频定高；多普勒；频谱；全相位快速傅里叶变换

Doppler Signal Spectrum Extraction Based on

0引言

调频多普勒定高引信是以地球表面为作用目标的测距系统。地面回波的产生机理非常复杂，依赖很多因素，如引信本身的工作参数、被测地物的介质特性以及系统所处的环境条件等等，地面回波信号实际为一个随机信号。因此，地面回波经混频、中频放大、二混频和低通滤波等处理得到的多普勒回波信号也会随机波动和衰减。基于多普勒信号的域特征如包络幅度变化的传统定高方法，通过对包络波峰进行检测，由于时域信号幅度稳定性差，故定高精度受限于地面反射特性的影响和调制频偏[1]。而频域处理方法如短时傅里叶变换(short-time Fourier transform ，STFT)通过对时域信号的频谱提取，克服了时域包络幅度特征不明显的缺陷，但无法有效抵制数据截断带来的频域上的频谱泄露[2]。为减少频谱泄露并有效分离信号幅度与频率等参数信息，许多文献提出整周期采样或对数据做加窗处理的改进方法[3]。前者在实际应用中容易受到采样频率偏差的影响，导致信号特征量提取精度降低；后者则在抵制旁瓣的同时，不可避免地引入了“主瓣模糊”的问题，故“加窗”不适合信号包含多个密集频率成分的情况[4]。本文针对上述问题，提出了基于全相位快速傅里叶变换(all-phase FFT，apFFT)的多普勒信号频谱提取方法。

1调频多普勒引信定高原理

1.1调频多普勒引信定高原理

对称三角波调频多普勒体制中，由于对称三角波只有偶次谐波分量没有奇次谐波分量，可以根据这一特点将接收差频的频率选在调制频率的偶次谐波上，以避免发射端调制频率的谐波对接收端造成干扰。对称三角波调频多普勒定高的原理就是基于：提取出来的多普勒信号的幅度主要随着差频幅度的变化而变化，而当引信和地面目标没有相对运动时，则无多普勒信号输出。

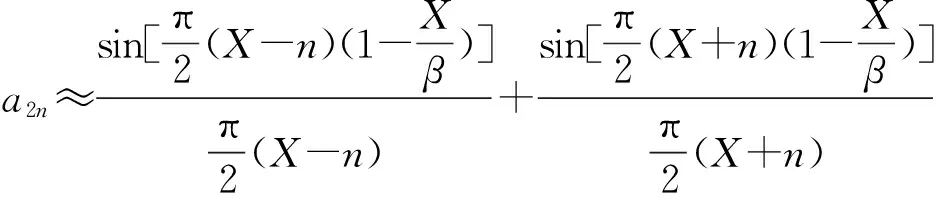
(1)

an近似为sinx/x形式，它是发射信号频偏和延迟时间(即高度)的函数，称为高度函数。而多普勒信号是用某次谐波对差频信号混频得到的。理想的多普勒信号可以表示为[5]

s(t)=a2ncos(2nπf0τ)cos[π(2n)fMτ]cos(2πfdt)

(2)

其中，fd为多普勒频率，f0为载频，fM为调制频率。

1.2基于短时傅里叶变换的频谱提取方法

短时傅里叶变换处理多普勒信号，是将信号加窗，将加窗后的信号再进行快速傅里叶变换，加窗后使得变换为时间t附近的很小时间上的局部谱，窗函数可以根据t的位置变化在整个时间轴上平移，利用窗函数可以得到任意位置附近的时间段频谱实现时间局域化[6]。基于短时傅里叶变换多普勒信号信息处理如图1所示。

图1中模块(3)短时傅里叶算法包括数据预处理和FFT。数据预处理是对每一帧数据加一个根据时频分辨率确定的窗函数。然后对每一帧加窗后的数据做FFT运算。窗函数根据工程要求可以选择N点的汉宁窗。

模块(4)特征提取：对FFT运算后的数据进行幅度提取是取每帧数据的最大频谱幅度为此帧数据的幅度估计，频率提取是取每帧数据最大频谱幅度对应的频率为此帧数据的频率估计。

模块(5)实时定高：设最大幅度的一半为阈值，以采样初始帧幅度估计为An，其后求取连续4帧数据的幅度估计的最大值为Amax，与阈值比较：若Amax递增五次，且都大于阈值时，确认峰值出现；否则，继续采样并且估计频谱幅度Amax作递增判断。此模块用于峰值识别。

图1　基于短时傅里叶变换调频多普勒引信信息处理功能框图Fig.1　FM Doppler fuze information processing block diagram based on short-time Fourier transform

1.3全相位快速傅里叶变换

全相位快速傅里叶变换(apFFT)算法是天津大学的王兆华和候正信教授提出的，具有初始相位不变和有效防止频谱泄露的特性。因为FFT是将截断的序列做周期延拓而得到无限长的序列的。当不是等间隔采样时，做周期延拓后，在首尾相接的地方就会出现信号的跳变，与原始信号不一致，在频谱上的表现就是频谱出现泄露[7]。全相位FFT频谱分析法具有优良的频率泄露抵制能力和相位不变性，适用于包含多个密集频率成分的频谱分析[8]。全相位快速傅里叶变换(apFFT)算法与短时傅里叶变换的区别在于数据预处理。短时傅里叶变换方法的数据预处理是对每一帧数据加一个根据时频分辨率确定的窗函数，然后作FFT运算。而全相位傅里叶变换(apFFT)算法的数据预处理则相对复杂，全相位FFT包括数据预处理和FFT算法两部分，其具体步骤是：

1)构成一个N点的汉宁窗；

2)汉宁窗对自己求卷积，得到2N-1点的卷积窗；

3)求2N-1点的卷积窗的和；

4)将卷积窗的每一项除以卷积窗的和，得到2N-1点的归一化卷积窗；

5)将数据的1：2N-1项和归一化卷积窗相乘，得到加窗的2N-1项；

6)将第1项和N+1项，第2项和N+2项…第N-1项和第2N-1项相加，得到经过全相预处理的N点序列；

7)进行FFT运算。

2多普勒信号频谱提取方法

用全相位FFT频谱分析对二混频后的多普勒回波作信息处理，提取幅度和频率特征参量，与短时傅里叶变换处理方法的不同之处在于中间算法模块，对应图1中的模块(3)、(4) ，亦即通过全相位FFT算法实时提取多普勒信号频谱幅度和频率，并对频谱幅度和频率进行估计，这个过程称为校正的apFFT算法。包括用apFFT算法实现模块(3)和特征提取模块(4)。

模块(3)用apFFT算法代替了原来的STFT算法。STFT和apFFT算法是都要进行FFT运算，只是在数据预处理时不同。常规STFT算法对每帧数据加汉宁窗就可送入FFT模块进行运算，而apFFT算法的数据预处理相对复杂，包括加窗等多项运算(见1.3节)。

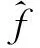
在特征提取，两种方法特征提取的目标都是幅度峰值，apFFT是取总体的数据统计，而STFT取最大值。两种方法提取的特征量通过模块(5)进行峰值识别。

3仿真验证

在Matlab环境下,根据调频多普勒引信定高参数，利用公式(2)产生理想多普勒信号s1。实测多普勒信号s2是在定高参数为表1的调频多普勒引信下实测得到的多普勒信号，故s1可视作s2的理想模型。以点频信号s0(t)=cos(2π×49.1t)为例，分别在周期采样和非周期采样的情况下，比较apFFT算法与STFT算法提取点频信号频谱的性能，即改善频率泄露的性能。然后将两种方法分别应用于信号s1和s2，提取时频曲线、频谱幅度与时间的关系曲线。设置峰值的一半为阈值，比较两种方法频谱幅度峰值的识别性能。

3.1点频信号仿真

目标信号s0(t)=cos(2π×49.1t)，是一个频率为49.1 Hz的余弦波。采样点数N=16。分两种情况进行仿真。1)周期采样的情况，采样频率fs1=49.1×16=785.6 Hz，是信号s0(t)频率的整数倍；2)偏离周期采样率的情况，fs2=512 Hz。则在两种情况下，信号s0(t)=cos(2π×49.1t)的频谱分别如图2、图3所示。

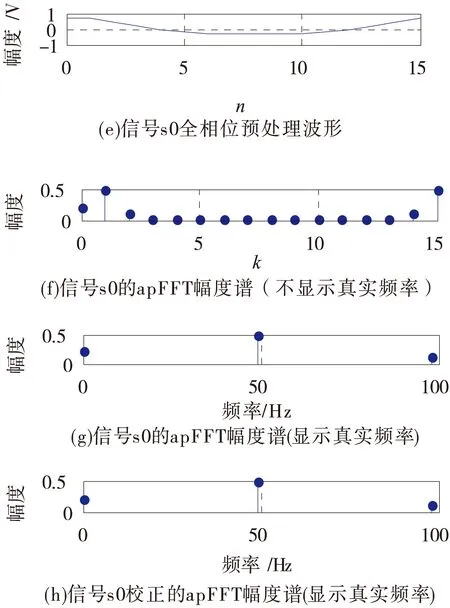
图2　在周期采样的情况下，信号s0(t)分别基于STFT和apFFT处理的幅度谱(采样率fs1=785.6 Hz)Fig.2　Spectrum of the signal based on STFT and apFFT respectively in the case of periodical sampling(sampling rate)

图3　在偏离周期采样率的情况下，信号s0(t)分别基于STFT和apFFT处理的幅度谱的幅度谱(采样率fs2=512 Hz)Fig.3　Spectrum of the signal based on STFT and apFFT respectively in the case of non-integer-period sampling(sampling rate)

从图2可看出，当采样率偏离0倍的周期采样率时，信号的首尾波形幅值是相同的，如图2(a)所示，若对观察区间进行周期为N的延拓，则求得矩形窗截断的波形所对应的谱线只有一根，不存在频谱泄露，如图2(b)所示。采样率偏离周期采样率，信号的首尾波形差异很大，如图3(a)所示，若对观察区间进行周期为N的延拓，其延拓后的信号必然会出现峰值的间断，一旦出现间断就意味着引入了很多高频成分而使得分析的波形失真，而这些由于截断引起的波形失真在频谱图上会以图3(b)所示的主谱线周围的泄露表现出来。

为解决由于截断引起的波形不连续及其频谱泄露问题，通常采用加窗的方法。从图2(c)、3(c)可看出，对截断信号加窗后，信号的首尾波形变得都连续了，这种波形连续在频谱图上以少数几根旁瓣谱线表现出来。但同时也可看出，采样频率一旦偏离周期采样频率，波形就会出现失真。需要注意的是，当采样频率没有偏离周期采样频率或者偏离程度很小时，泄露问题并不突出，但加窗后旁谱线的泄露反而突出起来，如图2(d)所示。

不管采样频率是否偏离周期采样频率，比较三种处理得到波形频谱的主谱线的旁瓣，发现经全相位数据预处理得到的波形，其apFFT幅度谱泄露均小于直接加窗截断所得波形的频谱泄露。虽然apFFT谱相比于加窗FFT谱抑制了频谱泄露，然而直接从apFFT谱图上读取幅度和频率信息，仍然是十分粗糙的。

3.2多普勒信号仿真

在Matlab环境下，根据调频多普勒引信前端定高参数，分别产生理想多普勒信号s1，并采集此系统输出的实际多普勒信号为实测多普勒信号s2，因为s1和s2出自同一个系统，可以预测，不考虑工程因素，两者的参数是一致的。下面验证基于STFT方法和基于校正apFFT方法对实测信号s2频谱提取的性能，并与理想多普勒信号s1的频谱作比较。

表1　调频多普勒引信定高参数

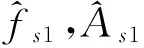
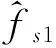
对于提取的频谱幅度，其峰值位置如表2所示。

表2　提取的频谱幅度峰值位置

值得一提的是STFT法提取的频谱幅度有多个峰值，在理想多普勒信号s1表现为类sinc函数，在实测信号s2表现为两个峰值差不多大。这表示已经很难区别哪个是主峰了；而此时校正apFFT的方法，其频谱幅度的副峰位置为(0.883 7,0.172 4) 。一般设置峰值的一半为阈值，0.172 4小于峰值的一半，依然很清晰地识别主峰。仿真结果与工程参数基本吻合，相对于STFT法，校正的apFFT法提取出来的特征量：即实测多普勒信号的频谱幅度，对峰值有很好的识别效果。这表明apFFT法更好地抑制了频谱泄露，而短时傅里叶变换法因为频谱泄露造成了估计出来的频谱的失真。仿真结果表明全相位FFT算法比短时傅里叶变换法更好的抑制了高频杂波，实时提取的幅度特性更明显，主峰特征明显，意味着全相位FFT算法能精确地识别峰值。当然，付出的代价是比短时傅里叶变换算法更加复杂。以提取出来的理想多普勒信号频谱为参照，得出校正的apFFT法提取的频谱比STFT法更贴近理想多普勒信号频谱，其频谱幅度信息满足峰值识别的要求。

图4　理想多普勒信号s1频谱提取Fig.4　Spectrum extraction of ideal Doppler signal s1

图5　实测多普勒信号s2频谱提取Fig.5　Spectrum extraction of actual Doppler signal s2

4结论

本文提出了基于全相位FFT的适用于调频多普勒信号的频谱提取方法。该方法采用全相位FFT算法实时获取多普勒回波信号的幅度信息，通过对幅度和频率进行修正，实时提取多普勒信号的幅度和频率，利用较为简单的幅度和频率融合判决算法检测峰值以达到定高的目的。Matlab仿真表明：全相位FFT提取的多普勒回波的频谱特征比短时傅里叶变换法更有效地减少了频谱泄露对峰值检测的影响，提取的频率更加贴近真实频率，提取的幅度更好的识别峰值，更加拟合理想多普勒信号包络。仿真结果与工程参数基本吻合，相对于短时傅里叶变换，校正的apFFT法提取的频谱比更贴近理想多普勒信号频谱，其频谱幅度信息满足峰值识别的要求。

参考文献:

[1]袁昆，曲家惠．连续波多普勒无线电引信的仿真和信号处理[J]．沈阳理工大学学报,2013，32(1)：38-40．

[2]谭思炜，任志良，孙常存．全相位FFT相位差频谱校正法改进[J]．系统工程与电子技术，2013，35(1)：35-36．

[3]Okarma K.Polynomial windows with low side-lobes’level[J].Signal Processing,2007,87(4):782-788.

[4]Agrez D.Improving phase estimation with leakage minimization[J].IEEE Trans.on Instrumentation and Measurement,2005,54(4):137-1353.

[5]赵惠昌．无线电引信设计原理与方法[M]．北京:国防工业出版社，2012．

[6]杜汉卿．无线电引信技术实验基础[M]．北京:北京兵器工业部教材审编室，1986．

[7]朱小勇，丁康．离散频谱校正法的综合比较[J]．信号处理，2001，17(1)：91-97．

[8]崔占忠，宋世和．近感引信原理[M]．北京：北京理工大学出版社，1995．

*收稿日期:2016-02-01

作者简介:雍得鹏(1985—)男，甘肃定西人，硕士研究生，研究方向：数字信号处理。E-mail:yongdepeng@163.com。

中图分类号:TJ434

文献标志码:A

文章编号：1008-1194(2016)03-0041-06

All Phase Fourier Transform

YONG Depeng，ZOU Jinlong，XIA Lei ，HAN Yinfu

(Science and Technology on Electromechanical Dynamic Control Laboratory，Xi’an 710065，China)

Abstract:Aiming at the problem of spectrum leakage due to the truncation effect and the fence effect, a method of spectrum extraction of Doppler signal based on all phase Fourier transform was proposed. The method obtained real-time Doppler echo signal amplitude information through the all phase fast Fourier transform algorithm, then the amplitude and frequency was calibrated. The simulation of theoretical and actual measured Doppler signal showed that, compared with the short time Fourier transform, the extracted spectrum of actual measured Doppler signal based on the corrected all phase fast Fourier transform algorithm was more proximate to the spectrum of the ideal Doppler signal and its spectrum amplitude information met the requirements of the peak identification.

Key words:fuze；frequency modulation height-fixed；Doppler；spectrum；all phase fast Fourier transform