基于盒维数的间歇采样转发干扰识别方法*

蒋莹，何明浩，郁春来，王冰切

(空军预警学院，湖北 武汉　430019)



探测跟踪技术

基于盒维数的间歇采样转发干扰识别方法*

蒋莹，何明浩，郁春来，王冰切

(空军预警学院，湖北 武汉430019)

摘要：间歇采样转发干扰是一种针对相干雷达的有效干扰样式，其对抗技术研究已经成为电子战领域的热点课题，而干扰识别历来是抗干扰技术中最关键的环节，针对间歇采样转发干扰的识别问题，提出了一种基于盒维数的干扰识别方法，将分形理论应用于间歇采样转发干扰的识别。通过对3类间歇采样转发干扰信号的产生原理及频谱进行分析，挖掘干扰及目标回波的分形特征，提取分形盒维数作为干扰识别的特征参数，并利用支持向量机进行分类识别，为后续雷达系统采取抗干扰措施提供先验信息。仿真结果证明该方法具有较高的识别概率。

关键词：间歇采样；干扰识别；特征提取；分形维数；盒维数；支持向量机

0引言

现代电子战中，雷达干扰与抗干扰之间的斗争正日趋激烈，特别是基于数字射频存储器(digital radio frequency memory，DRFM )的欺骗式干扰机，可以复制出与雷达发射信号具有相干性的干扰信号，从而在雷达接收机端获得相当大的相干处理增益，大大提高干扰效能，为雷达检测带来巨大挑战，已经成为了电子战中的主流对抗装备[1-4]。

随着应用的愈加广泛，基于DRFM的干扰技术近年来发展迅速，新的干扰样式不断涌现，文献[5]针对线性调频脉冲压缩雷达，提出了一种基于间歇采样转发的干扰技术，该技术立足于天线收发分时体制，通过对雷达信号进行低速间歇采样，巧妙地利用线性调频脉冲压缩雷达的匹配滤波特性，产生多假目标干扰。文献[6]深入研究了基于DRFM的多种干扰样式，在间歇采样直接转发的基础上，进一步提出了间歇采样重复转发干扰以及间歇采样循环转发干扰样式。新的干扰样式解决了特殊干扰平台(如弹载干扰机)下要求的高天线隔离度和工程实现之间的矛盾。

间歇采样转发干扰直接攻击线性调频脉冲压缩雷达的脉内相干性，可以使雷达产生多个逼真假目标，在一定条件下还可以产生压制干扰的效果。鉴于其干扰性能优越，间歇采样转发干扰不断得到改进，并用于干扰其他新体制雷达，其抑制与对抗迫在眉睫[7-9]。

众所周知，干扰识别是抗干扰流程中的关键环节，采取有效抗干扰措施的前提是正确进行干扰类型的识别。文献[10]提取了雷达复合干扰信号的盒维数及L-Z复杂度特征，对3种复合干扰信号进行了识别；文献[11]提取了干扰信号的积谱特征；文献[12]将小波分解理论应用于雷达有源欺骗干扰识别；文献[13]利用霍夫曼树建立识别模型，实现了待测干扰的识别。随着现代信号处理方法在抗干扰领域的应用，干扰识别方法不断创新发展，但针对间歇采样转发干扰识别的研究目前仍较为缺乏。

本文针对间歇采样转发干扰的识别问题，从信号处理的角度出发，将目标回波与干扰看做空间不同的模式类，利用干扰和目标回波信号在频谱上的差异，提取频谱盒维数特征，最后利用支持向量机对目标回波与干扰进行分类，实现干扰信号的检测与识别，为雷达抗干扰提供重要的决策信息，仿真结果验证了该方法的有效性。

1干扰产生原理

与传统的欺骗干扰样式通过人为地调制距离、速度或角度等信息来实现对雷达的欺骗不同，间歇采样转发干扰直接攻击雷达的脉内相干性，巧妙地利用对雷达信号的间歇性“欠采样”处理技术，可以使雷达产生多个逼真距离假目标，从而丧失探测与跟踪能力，为雷达检测带来巨大挑战。

1.1间歇采样直接转发干扰

对雷达发射的信号进行间歇采样直接转发处理，即截获到大时宽的雷达信号，高保真采样其中的一小段信号以后马上进行转发，然后再采样、处理转发下一段，采样转发分时交替工作，直到大时宽信号结束。干扰机的接收机和发射机在整个脉冲宽度内分时工作，其基本原理如图1所示。

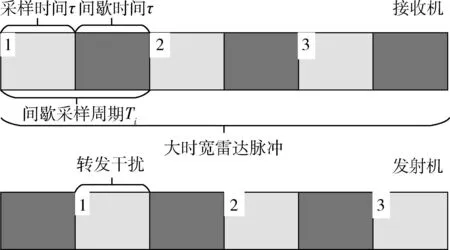
图1　间歇采样直接转发干扰基本原理Fig.1　Principle of interrupted-sampling repeater jamming

设雷达发射的信号为线性调频信号

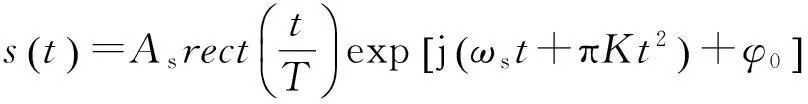
(1)

间歇采样信号为矩形包络脉冲串，其脉宽为τ，重复周期为Ts，包络脉冲为

(2)

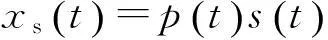
(3)

对一个脉冲宽度为T的线性调频信号，经过间歇采样周期为Ts、采样时长为τ为间歇采样处理，可以得到N个脉冲内为线性调频的窄脉冲，且N=⎣T/Ts」+1，⎣ 」表示向下取整。

其中，任意一个子脉冲信号可以表示为

(4)

式中：1≤n≤N，则采样信号为

(5)

那么，转发出去的干扰信号可以表示为

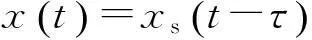
(6)

1.2间歇采样重复转发干扰

间歇采样重复转发的原理是，干扰机采样到雷达发射的一小段信号后，按照程序设定的次数重复读出当前采样信号并转发，然后再采样一小段信号并重复进行转发，如此重复上述过程，直到雷达脉冲结束。在雷达脉冲结束时，若最后一个采样转发的次数没有达到规定的次数，则继续转发直到达到规定的次数后为止。干扰机工作过程如图2所示。图中转发信号编码的第1位表示转发的信号是第几个采样，第2位表示该信号被转发的次数，如转发2-3表示第2个采样信号被第3次转发。

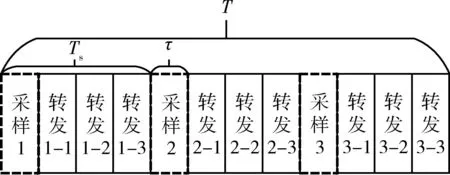
图2　重复转发的工作原理Fig.2　Principle of interrupted-sampling repetitive repeater jamming

设在间歇采样周期Ts内，可转发当前采样的次数为M,则M=⎣Ts/τ」-1。

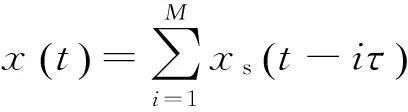
(7)

1.3间歇采样循环转发干扰

设脉冲持续时间T内可进行间歇采样的次数为N，间歇采样周期Ts内可转发采样信号的次数为M，则N=⎣T/Ts」+1，M=⎣Ts/τ」-1。

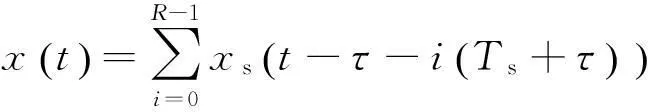
(8)

2干扰信号频谱分析

由式可知，间歇采样直接转发干扰信号的频谱与采样信号频谱理论上一致。脉冲宽度为100 μs，调频带宽为10 MBZ的线性调频雷达信号经过Ts=10 μs，τ=5 μs的间歇采样直接转发产生的干扰信

图3　循环转发的工作原理Fig.3　Principle of interrupted-sampling circular repeater jamming

号的频谱如图4所示。与目标回波信号的频谱(图5)相比可以发现，干扰信号幅度频谱的宽度和位置与目标回波信号基本相同，不同的是干扰信号频谱带内、带外均出现了许多起伏。带内起伏为各个子脉冲幅度频谱的体现，而带外起伏是各子脉冲频谱相互混叠导致的结果。

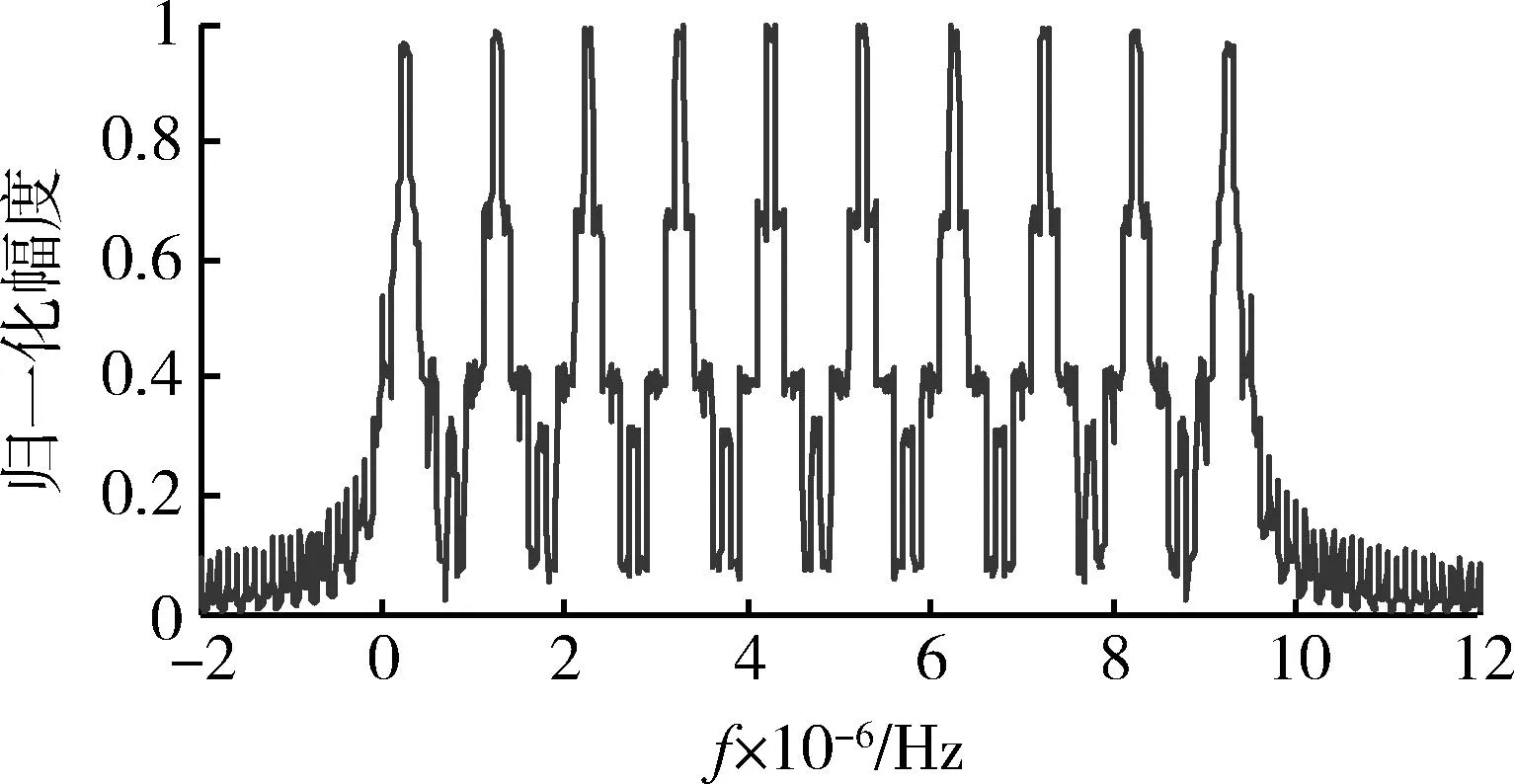
图4　间歇采样转发干扰频谱Fig.4　Frequency spectrum of interruptedsampling repeater jamming

图5　目标回波信号频谱Fig.5　Frequency spectrum of target echo

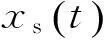
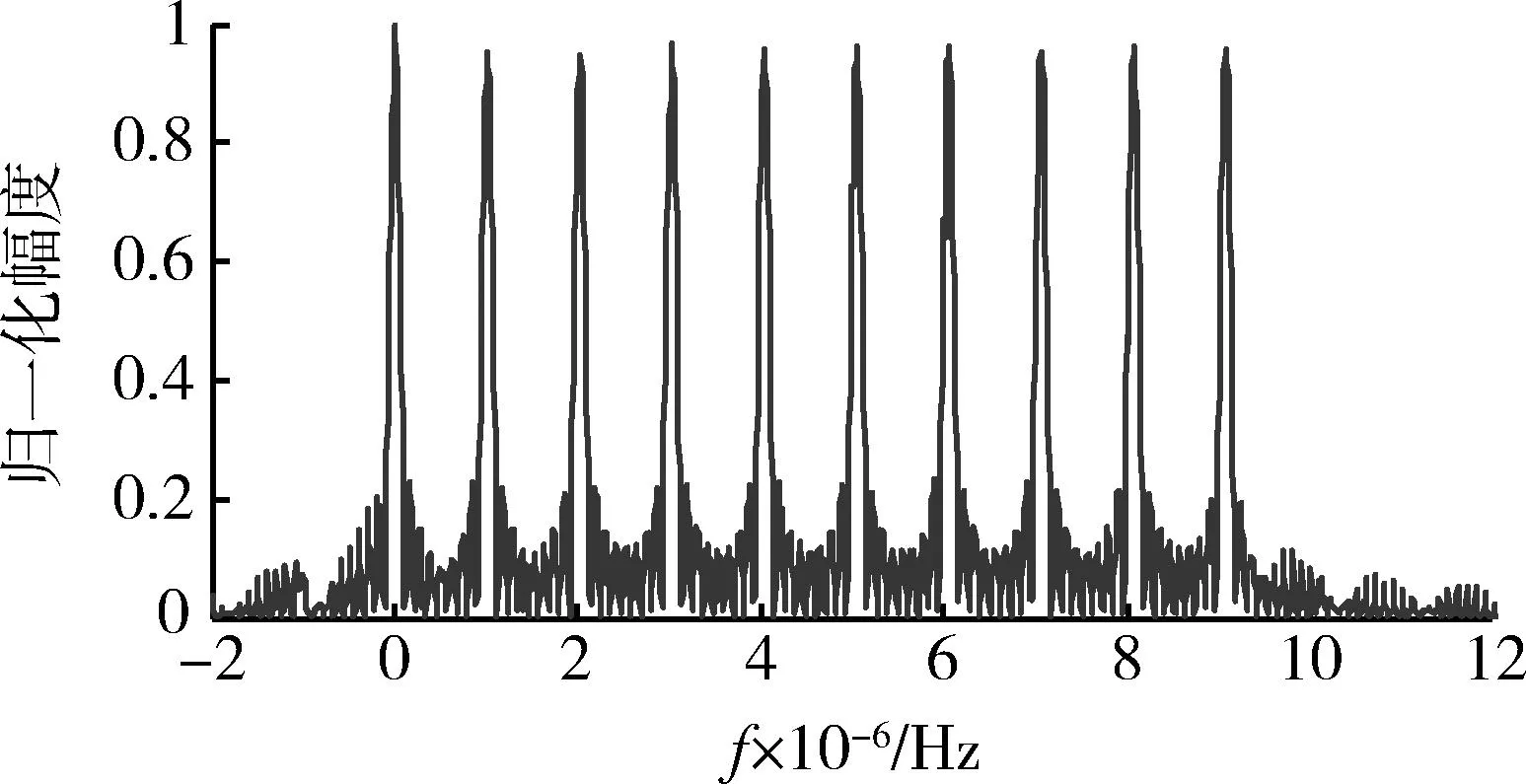
图6　间歇采样重复转发干扰信号频谱Fig.6　Frequency spectrum of interrupted-sampling repetitive repeater jamming

至于间歇采样循环转发干扰，与直接转发干扰、重复转发干扰一致，其频谱在宽度和位置上与目标回波信号频谱基本一致，主要的不同在于带内频谱分布。上述雷达信号经过Ts=10 μs，τ=2 μs的循环转发，产生的干扰信号频谱如图7所示。由于多处相邻转发信号之间相位存在突变，其带内频谱分布更为复杂。

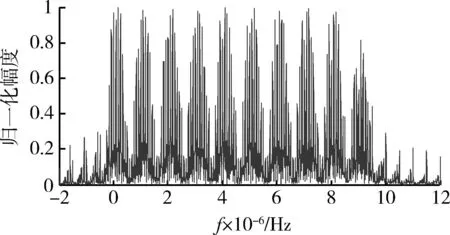
图7　间歇采样循环转发干扰信号频谱Fig.7　Frequency spectrum of interrupted-sampling circular repeater jamming

通过上述分析可以发现，3类间歇采样转发干扰经过傅里叶变换以后，频谱宽度及位置与目标回波信号基本相同，但在有效带宽内存在明显差异，利用这一差异，可以为干扰识别提供可能。

3特征参数提取

由上一节的分析可知，间歇采样转发干扰信号在频谱上与真实目标回波具有较大差异，虽然频谱的位置及宽度大致相同，但在有效带宽内，频谱分布各异。与真实目标回波相比，干扰信号的频谱更为复杂，带内起伏明显，间歇采样循环转发干扰尤为显著，直接转发干扰次之，重复转发干扰相比较之下则较为简单。本文立足于这一差异，力图挖掘可以表征干扰信号频谱复杂程度的特征参数以用于干扰识别。

分形盒维数是分形理论中的一种重要参数，它能定量描述分形集的复杂性和不规则性，反映分形集的几何尺度情况，且其计算简单、易于工程实现[14]。本文将分形理论应用至间歇采样转发干扰的特征提取中，提取干扰及回波的频谱盒维数，对信号频谱的复杂程度进行定量描述。

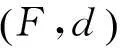
(9)

式中：f1,f2,…,fN是F的不同的点。

再设A是一个紧集，并且是非负的实数，若存在

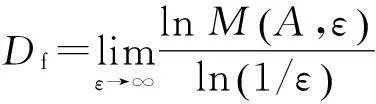
(10)

(11)

则盒维数为

(12)

本文提取频谱盒维数特征的算法流程如下：

(1) 将3类间歇采样转发干扰与目标回波信号从时域变换到频域，并对信号能量进行归一化处理，为提取频谱差异信息做好准备；

(2) 求出信号频谱的中心频率和有效带宽，并对带宽进行归一化处理，以减少特征提取的计算量，并排除带外噪声及载频的影响；

(3) 根据公式分别求取预处理后干扰及目标回波信号的频谱盒维数；

(4) 将频谱盒维数作为检测、识别间歇采样转发干扰所用的特征参数。

4仿真实验

为了验证本文算法的有效性，设置仿真条件如下：雷达发射的信号为线性调频信号，信号载频30 MBZ，带宽5 MBZ，脉宽100 μs，采样频率120 MBZ；间歇采样直接转发干扰的间歇采样周期为10 μs，采样占空比τ/Ts=0.5；重复转发干扰的采样周期为10 μs，采样时间1 μs，单个周期转发9次；循环转发干扰的采样周期为10 μs，采样时间1 μs；干信比0～10 dB，信噪比-5～25 dB。在不同干信比条件下，对每种干扰信号在每种信噪比下进行300次蒙特卡罗仿真，分别计算4种信号的频谱盒维数均值，得到结果如图8a)～c)所示。

图8　不同干信比条件下，盒维数均值随信噪比变化曲线Fig.8　Variation of mean value of box dimension with SNR under different JSR

观察图8可以发现，其一，目标回波与3类间歇采样转发干扰信号的频谱盒维数存在一定差异，虽然在某些信噪比处存在交叠，但除去交叠点以外，类间分离度较优；其二，干扰信号频谱盒维数受噪声的影响较小，且随着干信比的增加，干扰信号的频谱盒维数逐渐趋于稳定、不受噪声影响；其三，当信噪比足够大时，间歇采样循环转发干扰的频谱盒维数值最大，直接转发干扰次之，真实目标回波频谱盒维数值最小，这与第3节中信号频谱图所示的复杂度相一致，证明了盒维数表征频谱复杂程度的正确性。

为了验证本文算法的有效性，选用径向基核函数设计的支持向量机对4种信号进行分类识别，在干信比JSR=0 dB的条件下，对每种信号在信噪比为-5～25 dB时分别进行300次蒙特卡罗仿真，得到300个特征样本。选用其中100个样本进行分类器训练，200个样本用作信号识别测试，得到的识别准确率如图9所示。

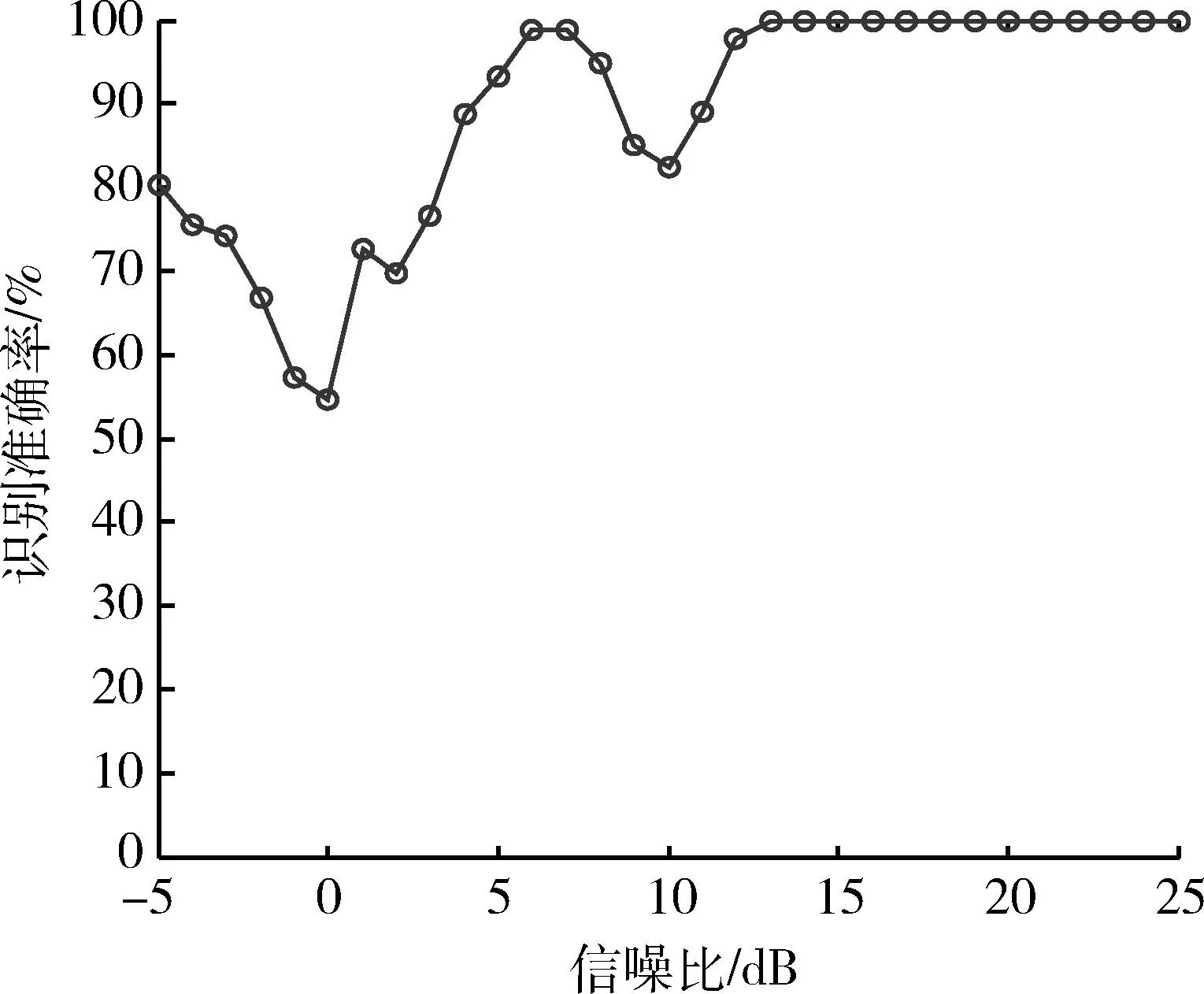
图9　JSR=0 dB时4种信号的平均识别准确率Fig.9　Average recognition accuracy while JSR is 0 dB

由图9可见，平均识别准确率在SNR=5 dB时已经超过了90%，但在SNR=10 dB左右出现了一定程度的下降，这是由于在SNR=10 dB时，真实目标回波与间歇采样重复转发干扰信号的频谱盒维数交叠导致的(见图8a))。SNR=0 dB处出现低谷的原因也类似。

为了进一步验证频谱盒维数作为特征参数的识别性能，将3种间歇采样转发干扰分别与真实目标回波进行组合，每个信噪比条件下进行300次蒙特卡罗仿真，得到300个样本，选取其中100个样本构成训练集，另外200个样本组成测试集，利用支持向量机进行识别，得到的识别准确率如图10所示。

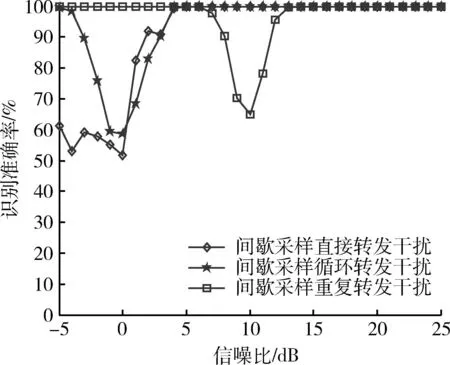
图10　JSR=0 dB时不同信号的识别准确率Fig.10　Recognition accuracy of different jamming while JSR is 0 dB

观察图10可以发现，间歇采样重复转发干扰和循环转发干扰的识别准确率分别在SNR=10 dB和SNR=0 dB左右出现了一定程度的下降，这与图8a)中信号频谱盒维数交叠的位置相一致。另外，即使在信噪比较低的情况下，间歇采样重复转发干扰的识别准确率也接近100%。对于间歇采样循环转发干扰而言，在SNR≥5 dB时，识别性能较优，均接近100%。而对于间歇采样直接转发干扰而言，由于在SNR≤0 dB时，干扰信号频谱盒维数与真实目标回波较为接近，识别准确率较低，但在信噪比较高(SNR≥5 dB)的条件下，识别准确率较高，均接近100%。

5结束语

本文针对间歇采样转发干扰的对抗问题展开研究，提出了基于分形盒维数的间歇采样转发干扰识别方法，将分形理论应用于间歇采样转发干扰的识别，利用干扰信号与目标回波信号在频谱上的差异，提取信号的频谱盒维数作为干扰识别的特征参数，并选取支持向量机作为分类器进行了干扰识别实验，仿真结果表明，该方法是有效的，且具有较高的识别准确率，能有效区分间歇采样转发干扰与真实目标回波，可以为雷达采取有效的抗干扰措施提供重要的决策信息。

参考文献：

[1]OLIVIER K,CILLIERS J E,PLESSIS M Du. Design and Performance of Wideband DRFM for Radar Test and Evaluation[J]. Electronics Letters, 2011, 47(14): 824-825.

[2]Scott D Berger. Digital Radio Frequency Memory Linear Range Gate Stealer Spectrum[J]. Transactions on Aerospace and Electronic System， 2003，39( 2): 725-735.

[3]孙智勇，唐宏，余定旺,等. 基于DRFM的机载PD雷达干扰研究[J]. 现代防御技术, 2012, 40(4): 138-142.

SUN Zhi-yong, TANG Hong, YU Ding-wang, et al. Interference on Airborne PD Radar Using DRFM-Based Technology [J] . Modern Defence Technology, 2012, 40(4): 138-142.

[4]赵锋，王雪松，肖顺平，等. 现代雷达电子战系统建模与仿真[M]. 北京: 电子工业出版社，2010.

ZHAO Feng, WANG Xue-song, XIAO Shun-ping， et al. Modeling and Simulation of Modern Radar and Elecreonic Warfare Systems[M]. Beijing: Publishing House of Electronic Industry， 2010.

[5]王雪松，刘建成，张文明，等. 间歇采样转发干扰的数学原理[J]. 中国科学E辑:信息科学, 2006, 36(8): 891-901.

WANG Xue-song, LIU Jian-cheng, ZHANG Wen-ming, et al. Mathematics Principles of Interrupted-Sampling Repeater Jamming [J] . Science China (Ser-E), 2006, 36(8): 891-901.

[6]刘忠. 基于DRFM的线性调频脉冲压缩雷达干扰新技术[D].长沙:国防科学技术大学,2006.

LIU Zhong. Jamming Technology for Countering LFM Pulse Conpression Rader Based on Digital Radio Frequency Memory [D] . Changsha: National University of Defense Technology, 2006.

[7]吴晓芳，王雪松，卢焕章. 对SAR的间歇采样转发干扰研究[J]. 宇航学报, 2009, 30(5): 2043-2048.

WU Xiao-fang, WANG Xue-song, LU Huan-zhang. Study of Intermittent Sampling Repeater Jamming to SAR [J] . Journal of Astronautics,2009, 30(5): 2043-2048.

[8]郭雷，李宏，李青山. 相参雷达间歇采样灵巧干扰方法[J]. 现代防御技术, 2013, 41(3): 111-116.

GUO Lei, LI Hong, LI Qing-shan. Interrupted Sampling Smart Jamming Method for Coherent Radar [J] . Modern Defence Technology, 2013, 41(3): 111-116.

[9]冯德军，王伟，徐乐涛. 对V-调频信号的间歇采样转发干扰研究[J]. 雷达科学与技术, 2013, 11(2): 209-213.

FENG De-jun, WANG Wei, XU Le-tao. Jamming V-FM Signal Using Interrupted-Sampling Repeater [J] . Radar Science and Technology, 2013, 11(2): 209-213.

[10]熊英，刘旻，唐斌，等. 基于盒维数与L—Z复杂度的雷达复合干扰特征提取方法[J]. 数据采集与处理, 2008, 23(6): 663-667.

XIONG Ying, LIU Min, TANG Bin, et al.Feature-Extracting Method for Radar Compound Jamming Signal Based on Box Dimension and L-Z Complexity [J] . Journal of Data Acquisition & Processing, 2008, 23(6): 663-667.

[11]TIAN Xiao, TANG Bin, GUI Guan. Product Spectrum Matrix Feature Extraction and Recognition of Radar Deception Jamming[J]. International Journal of Electronics，2013， 100(12): 1621-1629.

[12]田晓，唐斌. 基于归一化小波分解能量比的雷达有源欺骗干扰识别[J]. 数据采集与处理, 2013, 28(4): 416-420.

TIAN Xiao, TANG Bin. Active Deception Jamming Recognition of Radar Based on Normalized Wavelet Decomposition Power Ratio [J] . Journal of Data Acquisition & Processing, 2013, 28(4): 416-420.

[13]李芳，熊英，唐斌. 基于霍夫曼树和逆云模型的雷达拖引干扰识别[J]. 数据采集与处理, 2013, 28(4): 497-501.

LI Fang, XIONG Ying, TANG Bin. Identification of Radar Pull-off Jamming Based on Huffman Tree and Backward Cloud Model [J] . Journal of Data Acquisition & Processing, 2013, 28(4): 497-501.

[14]刘文涛，陈红，蔡晓霞，等. 基于分形维数的数字调制信号识别[J]. 火力与指挥控制, 2014, 39(10): 88-90.

LIU Wen-tao;CHEN Hong，CAI Xiao-xia, et al. Digital Modulation Signal Identification Based on Fractal Dimension [J] . Fire Control & Command Control, 2014, 39(10): 88-90.

[15]谢和平，薛秀谦. 分形应用中的数学基础与方法[M]. 北京: 科学出版社,1998.

XIE He-ping, XUE Xiu-qian. Mathematical Foundation and Method of Application of Fractal Theory [M] . Beijing: Science Publishing Company, 1998.

[16]吕铁军，郭双冰，肖先赐. 调制信号的分形特征研究[J]. 中国科学E辑:技术科学, 2001, 31(6): 508-513.

LÜ Tie-jun, GUO Shuang-bing, XIAO Xian-ci. Research of Fractal Features of Modulation Signal [J] . Science China (Ser-E), 2001, 31(6): 508-513.

Method of Interrupted-Sampling Repeater Jamming Recognition Based on Box Dimension

JIANG Ying，HE Ming-hao, YU Chun-lai, WANG Bing-qie

(Air Force Early Warning Academy，Hubei Wuhan 430019, China)

Abstract:Interrupted-sampling repeater jamming (ISRJ) is a valid jamming mode for coherent radar and suppression studying and it has become a hot topic in electronic warfare (EW). As we all know, jamming recognition is the key link of the antijamming system. Aiming at recognition of ISRJ, fractal theory is applied to identification and a jamming recognition scheme is proposed based on fractal box dimension. Firstly, we analyze the generation principle and frequency spectrum of jamming signals. Then the fractal box dimension is extracted and used as a feature parameter to discriminate target and jamming. Finally, the support vector machine is adopted to classify the target and jamming so that the priori information can be provided for radar system to select antijamming method. The simulation results show high recognition probability.

Key words:interrupted-sampling; jamming recognition; feature extraction; fractal dimension; box dimension; support vector machine

*收稿日期：2015-04-24；修回日期：2015-07-07

作者简介：蒋莹(1991-)，女，江苏南京人。博士生，研究方向为电子对抗信息处理。

通信地址：430019湖北省武汉市江岸区黄浦大街288号研管21队E-mail：jty614@163.com

doi:10.3969/j.issn.1009-086x.2016.02.025

中图分类号：TN974

文献标志码：A

文章编号：1009-086X(2016)-02-0157-08