基于级数反演的方位NCS成像算法分析*

邢涛，胡庆荣，李军，王冠勇

(北京无线电测量研究所，北京　100854)



探测跟踪技术

基于级数反演的方位NCS成像算法分析*

邢涛，胡庆荣，李军，王冠勇

(北京无线电测量研究所，北京100854)

摘要：斜视SAR成像时，存在方位空变现象，方位空变减小了方位聚焦深度，可通过方位NCS增大方位聚焦深度。在进行方位NCS时，忽略高次项对驻相点的影响会造成成像精度的降低甚至散焦。采用级数反演方法计算方位NCS的驻相点，提高了驻相点的计算精度，更新了高次变标系数及校正函数。仿真结果表明，采用级数反演计算驻相点后，点目标聚焦效果改善明显，较好地增大了方位聚焦深度。

关键词：合成孔径雷达; 高分辨; 方位; 非线性变标; 级数反演; 分析;

0引言

斜视SAR成像算法有基于倾斜谱[1-3]的成像算法和基于正交谱[1,4-6]的成像算法，基于正交谱的成像算法通过距离走动校正处理，降低了信号距离、方位两维耦合，增强了正交性。在正交谱成像处理模式下，成像结果存在方位空变现象，点目标在方位向散焦。文献[7]提出了基于NCS原理的方位非线性变标方法，该方法能使点目标在方位向聚焦，但是存在方位形变的问题，需要插值校正形变。文献[8]提出了新的方位变标方式，通过构造三次相位，避免了形变的产生，并对方位NCS后残留高次相位及变标因子的选取进行了系统地分析。文献[9-11]的三次方位NCS源自于距离维DeChirp处理后的距离时域、方位时域信号，第一次变标即从方位时域开始。文献[12]与文献[8]一样，首次变标从距离维CS处理后的距离时域、方位频域开始，并且采用四次方位NCS，在高精度成像中能取得更好的效果。

驻相点的精确求取主要有2种方法，最直接的方法为对一元二次方程或一元三次方程求根，高次方程求根涉及到判别式正负及复根问题，根的计算、取舍及显式解的获取都比较困难。另外一种相对精确求取驻相点的方法是级数反演方法，级数反演是多项式级数与其反函数间的变换公式[13-15]。在方位NCS部分，采用四次变标，驻相点计算时仍然忽略了高次项的影响。本文距离维处理与文献[8,12]一样，采用CS处理，方位首次变标从方位频域开始。文献[8-12]方位NCS过程中驻相点的求取均忽略了三次或四次项的影响。在高分辨高精度成像中，驻相点不精确将导致图像散焦，造成方位聚焦深度下降。

本文把级数反演与方位NCS驻相点的求取相结合，给出了基于级数反演的四次方位NCS成像算法及对应的变标系数。另外，距离维CS处理后，除了方位原本相位项，还存在因距离维CS处理而残留的相位项，文献[8]，式(23)给出了该残留相位项表达式，并指出可于第一次方位频域变标时一并把残留项校正掉。然而文献[8]给出的残留项并不完全，因为文献[8,12]在距离维CS过程中，均忽略了方位偏移对距离驻相点的影响，在高分辨成像中，这种影响会给方位NCS处理增添附加的残留相位，并制约方位NCS的性能。本文分析了距离维处理给方位NCS带来的附加相位的表达式及其对方位NCS成像的影响，并进行了仿真验证。

1方位NCS处理

斜视成像几何关系如图1所示。

图1　斜视成像几何关系Fig.1　Squint imaging geometry

斜距为

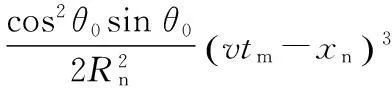
(1)

令

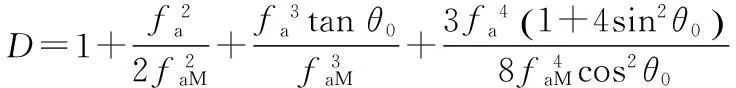
(2)

(3)

可得距离走动校正之后的二维谱[8,12]为

(4)

(5)

式(5)中最后一个指数项即为距离CS处理的残留项。令Rr=Rn+xnsinθ0，xn=vt0，定义校正函数及变标函数：

(6)

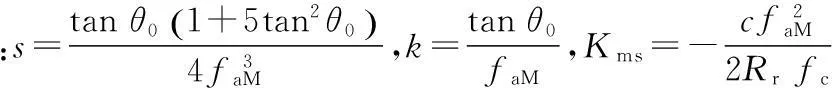
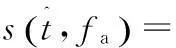
(7)

令：K3=K1-k2t0，K4=K2-st0，把K3，K4代入式(7)，进行方位IFFT，忽略高次项对驻相点的影响，得

(8)

定义变标函数：

(9)

令

(10)

式(8)乘以式(9)，进行方位FFT，得

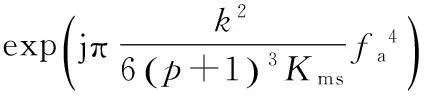
(11)

定义校正函数：

(12)

式(11)乘以式(12)，得

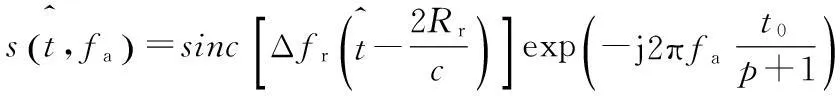
(13)

式(13)方位IFFT，得

(14)

式中:p的选取方法可参考文献[8,12]。成像算法流程如图2所示。

图2　成像流程图Fig.2　Flow chart of imaging algorithm

2基于级数反演的方位NCS

经过级数反演计算[7]，得到新的变标系数：

(15)

与式(11)对应的方位频谱为

(16)

比较式(16)与式(11)，可以发现，采用级数反演方法计算方位NCS过程中的时域及频域驻相点后，变标因子K1，K5，K6没有发生变化，而与四次项对应的变标因子K2，K7发生了改变。接下来方位校正相应更新式(12)即可，成像流程如图2所示。

3仿真实验及分析

仿真系统参数如表1所示，点目标设置如图3所示，仿真结果如图4、图5所示。

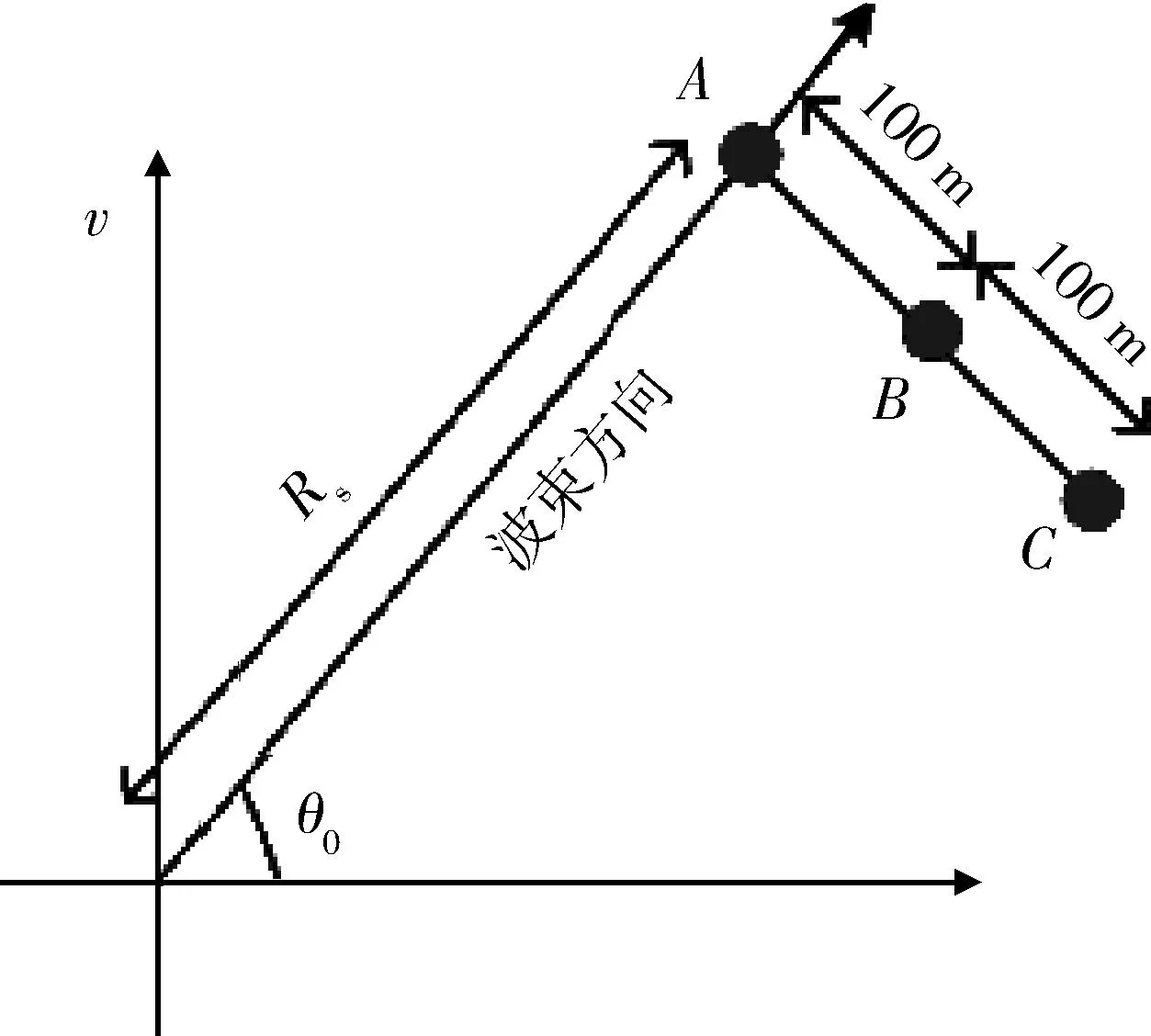
图3　点目标设置示意图Fig.3　Point targets setting

图5与图4对比表明：经过级数反演计算驻相点后，小斜视角时C点聚焦效果有了非常明显的改善。但在大斜视角时，B和C点均有不同程度的散焦，下面对原因进行分析。

表1　仿真参数

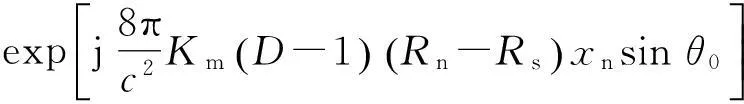
(17)

图6表明：附加相位项的相位随斜视角大小成正比增加，在10°斜视角时，该附加项在B和C点相位小于π/4，可以忽略，不影响聚焦；30°斜视角时，该附加项在C点的相位大于π/4，会降低C点聚焦质量；在60°斜视角时，附加项在B点和C点相位均大于π/4，尤其是C点，散焦现象比较严重。附加项的存在限制了方位NCS能处理的最大方位有效偏移量。文献[13]把距离CS及方位NCS混合在一起交替进行处理，能较大地拓展方位聚焦深度。文献[15]采用等效阵列重采样的方式达到较大的方位聚焦深度。上述两种方法均是基于方位全孔径进行的，不适宜应用在某些基于方位分块运动补偿与成像处理的实测数据处理中。

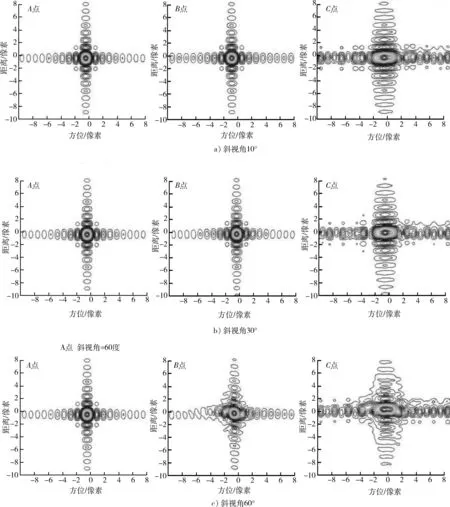
图4　方位NCS成像结果Fig.4　Imaging results of azimuth NCS

图5　基于级数反演的方位NCS成像结果Fig.5　Imaging results of azimuth NCS based on series reversion

图6　附加相位项的相位Fig.6　Phase of additional phase term

4结束语

本文把级数反演应用到方位NCS的驻相点计算上，在高分辨成像中，能较好地增强点目标的聚焦效果。针对大斜视角下点目标的散焦现象，文中分析了原因，主要是由于距离维CS处理给方位NCS产生的附加项相位过大的原因，该相位对点目标的方位偏移大小非常敏感，附加相位项的存在限制了高分辨大斜视SAR方位NCS的性能。

参考文献：

[1]AN Dao-xiang，LI Yang-huan, HUANG Xiao-tao,et al. Performance Evaluation of Frequency-Domain Algorithms for Chirped Low Frequency UWB SAR Data Processing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2014, 7(2): 678-690.

[2]SUN Guang-cai, XING Meng-dao, LIU Yan, et al. Extended NCS Based on Method of Series Reversion for Imaging of Highly Squinted SAR[J]. IEEE Geoscience and Remote Sensing letters, 2011, 8(8): 446-450.

[3]LI Dong, LIAO Gui-sheng, WANG Wei, et al. Extended Azimuth Nonlinear Chirp Scaling Algorithm for Bistatic SAR Processing in High-Resolution Highly Squinted Mode[J]. IEEE Geoscience and Remote Sensing letters, 2014, 11(6): 1134-1138.

[4]IRAOLA P P, SCHEIBER R, MAROTTI L, et al. TOPS Interferometry with TerraSAR-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3179-3188.

[5]WANG Yan, LI Jing-wen, CHEN Jie, et al. A Parameter-Adjusting Polar Format Algorithm for Extremely High Sqint SAR Imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 640-650.

[6]XING Meng-dao, WU Yu-feng, ZHANG Yi-min , et al. Azimuth Resampling Processing for Highly Squinted Synthetic Aperture Radar Imaging with Several Modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4339-4352.

[7]Frank H Wong，Tat Soon Yeo. New Applications of Nonlinear Chirp Scaling in SAR Data Processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(5): 946-953.

[8]SUN Guang-cai, JIANG Xiu-wei, XING Meng-dao, et al. Focus Improvement of Highly Squinted Data Based on Azimuth Nonlinear Scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2308-2322.

[9]邢涛, 胡庆荣, 李军，等. 毫米波高分辨SAR成像算法性能分析[J]. 现代防御技术, 2015, 43(1): 81-86.

XING Tao, HU Qing-rong, LI Jun, et al. Analysis of Millimeter Wave High Resolution SAR Imaging algorithm[J]. Modern Defence Technology, 2015, 43(1): 81-86.

[10]朱江, 廖桂生, 朱圣棋. 空间目标成像中基于FrFT的高精度距离压缩方法[J]. 系统工程与电子技术, 2015, 37(2): 271-277.

ZHU Jiang, LIAO Gui-sheng, ZHU Sheng-qi. High Precision Range Compression Based on FrFT for Space Target Imaging[J]. Systems Engineering and Electronics, 2015, 37(2): 271-277.

[11]LIU Gao-gao, ZHANG Lin-rang, LIU Nan, et al. Focusing Highly Squinted Data Using the Extended Nonlinear Chirp Scaling Algorithm[J]. IEEE Geoscience and Remote Sensing letters, 2013, 10(2): 342-346.

[12]AN Dao-xiang, HUANG Xiao-tao, JIN Tian, et al. Extended Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Data Focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(9): 3595-3609.

[13]ZHANG Shuang-xi, XING Meng-dao, XIA Xiang-gen, et al. Focus Improvement of High-Squint SAR Based on Azimuth Dependence of Quadratic Range Cell Migration Correction[J]. IEEE Geoscience and Remote Sensing letters, 2013, 10(1): 150-154.

[14]田超, 文树梁. 互耦条件下方位全向米波雷达测角算法[J]. 现代防御技术, 2015, 43(1): 94-99.

TIAN Chao, WEN Shu-liang. Angle Measuring Algorithm with Mutual Coupling of Azimuth Omni-Directional VHF Radar[J]. Modern Defence Technology, 2015, 43(1): 94-99.

[15]WU Yu-feng, SUN Guang-cai, XIA Xiang-gen, et al. An Azimuth Frequency Non-Linear Chirp Scaling(FNCS) Algorithm for TOPS SAR Imaging with High Squint Angle[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(1): 213-221.

Analysis of Azimuth NCS Imaging Algorithm Based on Series Reversion

XING Tao，HU Qing-rong，LI Jun，WANG Guan-yong

(Beijing Institute of Radio Measurement, Beijing 100854, China)

Abstract:In squint SAR imaging, there exists azimuth varying phenomenon which reduces the depth of azimuth focus. Azimuth NCS can increase the depth of focus. During azimuth NCS, ignoring the impact of high-order terms to the stationary phase point will result in lower imaging precision even defocus. A method of calculating the stationary phase point by series reversion in azimuth NCS is proposed. The proposed method improves the stationary phase point accuracy by updating the high-order terms coefficients and correction functions. The simulation results show that after adopting the series reversion method for stationary phase point computation, point target focusing effect improves significantly and the depth of azimuth focus increases.

Key words:synthetic aperture radar(SAR); high-resolution ; azimuth; nonlinear chirp scaling(NCS); series reversion; analysis

*收稿日期：2015-02-09；修回日期：2015-05-28

基金项目：有

作者简介：邢涛(1986-)，男，湖北黄梅人。博士生，研究方向为雷达成像技术。

通信地址：北京142信箱203分箱1号E-mail：1mingzongyue@163.com

doi:10.3969/j.issn.1009-086x.2016.02.022

中图分类号：TN957.52；TP391.9

文献标志码：A

文章编号：1009-086X(2016)-02-0135-08