基于电磁兼容分析的舰载雷达优化部署方法*

方小星，朱志宇，张冰，李阳

(江苏科技大学 电子信息学院，江苏 镇江　212003)



基于电磁兼容分析的舰载雷达优化部署方法*

方小星，朱志宇，张冰，李阳

(江苏科技大学 电子信息学院，江苏 镇江212003)

摘要：针对舰载雷达频谱拥挤，频率相近或相同雷达之间存在电磁兼容的问题，提出了一种基于电磁兼容分析的雷达优化部署方法。针对由定向天线和全向天线雷达组成的雷达系统，建立了电磁兼容模型，将其作为适应度函数，运用粒子群算法对雷达进行优化部署。仿真结果表明，应用粒子群算法结合电磁兼容模型，可以很好地解决雷达的优化部署问题。

关键词：电磁兼容；雷达天线；度量模型；舰载雷达系统；粒子群；优化部署

0引言

在海战场上雷达林立，尤其是雷达工作频谱拥挤的情况下，相近和相同频率雷达同时工作时会产生严重的电磁兼容问题[1-3]，这时候需要对雷达进行优化部署。现有的文献一般只考虑雷达对责任区的覆盖，将覆盖系数和重叠系数为主要优化目标[4-7],这种方法主要从对主要方向、主要高度层中的目标区覆盖冗余数最多、体积最大以及单部雷达对目标的覆盖系数最大两个方面进行优化部署。少数文献考虑了雷达的探测概率，通过提高雷达探测概率来优化雷达组网[8-10]，给出了单部雷达探测概率和组网雷达联合探测概率模型，通过分析模型与雷达位置的关系来实现优化部署。然而上述文献忽略了雷达间存在的电磁兼容问题，尤其在频谱拥挤的情况下。本文提出了一种将雷达间的电磁兼容作为雷达优化目标，结合粒子群算法对雷达进行优化部署的方法。

1舰载雷达电磁兼容模型

假设有N部雷达同时工作，且存在同频干扰。那么可知第n个雷达受到其他雷达的干扰Prn可表示为

Prn=Pn1+Pn2+…+Pn(n-1)+Pn(n+1)+

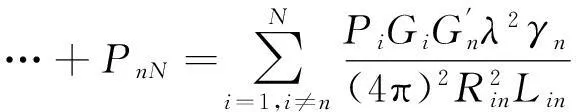
(1)

此时，雷达n收到的目标信号功率Prs为[11]

(2)

式中：Pn为雷达n发射功率；Gn为雷达n天线增益；σ为目标散射截面积；Ln为雷达发射并接收电磁波过程中的能量损耗；Rn为雷达n与目标的距离。

在受干扰条件下，雷达要能发现目标，收到的目标信号功率Prs和接收的干扰功率Prn必须满足以下条件：

(3)

式中：Kn为第n个雷达的压制系数。

当Prn/Sn min≤Kn时，雷达的最大作用距离不受影响。当Prn/Sn min>Kn时，可以得到干扰下的雷达最大作用距离[12]：

(4)

1.1全向天线雷达之间的电磁兼容模型

雷达有许多种类，但是通过雷达天线种类可以将其分为2种：采用定向天线的雷达和采用全向天线的雷达。由于全向天线波束简单，首先建立全向天线雷达之间的电磁兼容模型。

(5)

由N部全向天线雷达组成的雷达系统的电磁兼容程度为

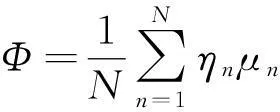
(6)

式中：ηn为第n个雷达的重要系数，根据作战要求对雷达的要求度确定。

1.2全向天线与定向天线雷达之间电磁兼容模型

当存在定向天线时，被定向天线对准，接收机前端会出现过载现象，电磁兼容程度很差，可认为电磁兼容程度μ=0。假设，有M个定向天线雷达对全向天线雷达n有干扰。定向天线雷达i对全向天线雷达n的对准概率pni，那么雷达n不被对准的概率为

(7)

第n个雷达与定向雷达的电磁兼容程度为

(8)

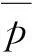
(9)

第k个定向天线雷达与全向天线雷达的电磁兼容程度可表示为

(10)

1.3定向天线雷达之间的电磁兼容模型

对于2个定向天线雷达之间的电磁兼容问题显然不能直接完全用上述模型来预测雷达间的电磁兼容程度。当2个定向天线雷达的主瓣波束不能相互对准的时候，模型与上述相同。当2个定向天线雷达的主瓣波束可以相互对准时，既需要避免对其他天线的对准也需要避免对准其他天线。

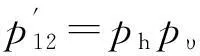
(11)

式中：Ph为水平方位对准概率；Pυ为俯仰方位对准概率。

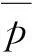
(12)

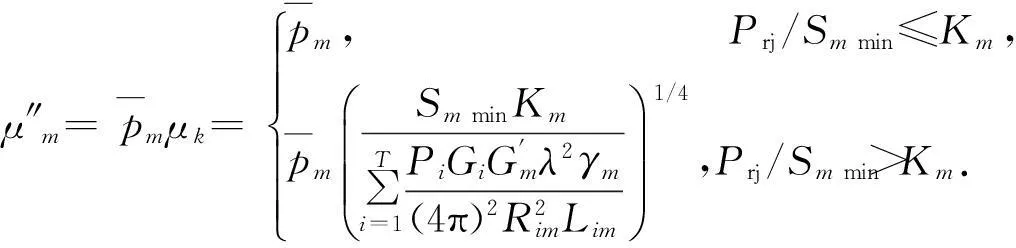
(13)

1.4雷达系统的电磁兼容模型

将相近或相同频率的雷达组成雷达系统，应用上述电磁兼容模型，可以预测整个雷达系统的电磁兼容程度。假设有N个全向天线雷达，K个定向天线雷达，其中有M个定向天线雷达有可以两两对准的雷达。雷达系统的电磁兼容程度为

(14)

式中：ηn是第n个全向天线雷达的重要系数；εk，εm为第k，m个定向天线雷达的重要系数。

2基于电磁兼容的舰载雷达位置优化部署方法

采用粒子群算法对雷达位置进行优化部署，而对舰载雷达优化部署就是对舰船编队时的位置进行优化。用Xi表示n维搜索空间中粒子i的当前位置，Vi表示当前粒子的飞行速度，Pi表示当前粒子所经历的最好位置[15-16]。

(15)

式中：n表示维度；i表示第i个粒子(当前粒子)。

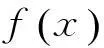
(16)

式中：t表示第t次迭代。

设群体中粒子数为S，群体中所有粒子所经历过的最好位置为Pg(t)(最优位置)，可得：

(17)

基本粒子群算法粒子i的进化方程可描述为

vij(t+1)=wvij(t)+c1r1j(t)(Pij(t)-xij(t))+

c2r2j(t)(Pgj(t)-xij(t)),

(18)

xij(t+1)=xij(t)+vij(t+1)，

(19)

式中：xij(t)，vij(t)表示粒子i第j维第t代的位置与运动速度；w为惯性系数，值在0～1之间；c1，c2为加速度常数，值在0～2之间；r1j，r2j分别为2个相互独立的随机数，值在0～1之间；Pgj(t)表示第j维最优位置粒子。

将雷达的电磁兼容程度作为雷达位置优化部署的适应度函数，在已知雷达参数的情况下，当雷达工作在相近或相同频率时，以满足作战要求为前提确定雷达的位置空间范围，运用粒子群算法对雷达的部署进行优化。基于电磁兼容分析的雷达优化部署方法的步骤：

(2) 不考虑不同时间的雷达使用与否与重要度系数变化，只分析此时的位置对雷达对准的概率影响，确定此时的总电磁兼容程度。

(3) 对粒子进行选择:①假设以概率1选择所有Xi；②通过公式(14)计算每个粒子的Φ总，通过公式(16)求出当前所有粒子的最优位置；③运用公式(17)求得种群中到目前为止在搜索空间找到的最好粒子，即最优位置。

(4) 对粒子进行繁殖：①利用公式(19)求出更新后的速度；②利用公式(20)求出更新后的t+1代的粒子群，即位置。

(5) 判断是否达到迭代次数：若是，直接输出当前最优位置；若不是，则令t=t+1，转入第⑵步。

(6) 结束，输出最后的最优位置。

此方法默认各雷达的工作情况不变，忽略时间这一维度，只从空间角度来简化问题。最后用算例来说明方法的有效性。

3算例分析

以3部雷达为例，表1给出3部雷达的参数。

3部雷达分别为表1中的雷达A、雷达B和雷达C，用圆圈表示它们的位置，如图1所示。

雷达A在x2+y2=1 600,(0≤x≤40)的范围内满足作战需求，雷达B在x轴上，雷达C在y轴上。雷达C扫描范围为以雷达C为圆心顺时针从y轴扫描60°，雷达B扫描范围在x轴下方。显而易见，雷达A在边界上得到的Φ比在边界以内大。用上述粒子群算法对其进行优化分布，得到的雷达位置优化结果如表2～4所示。

表1　雷达的主要技术参数

图1　雷达分布图Fig.1　Radar maps

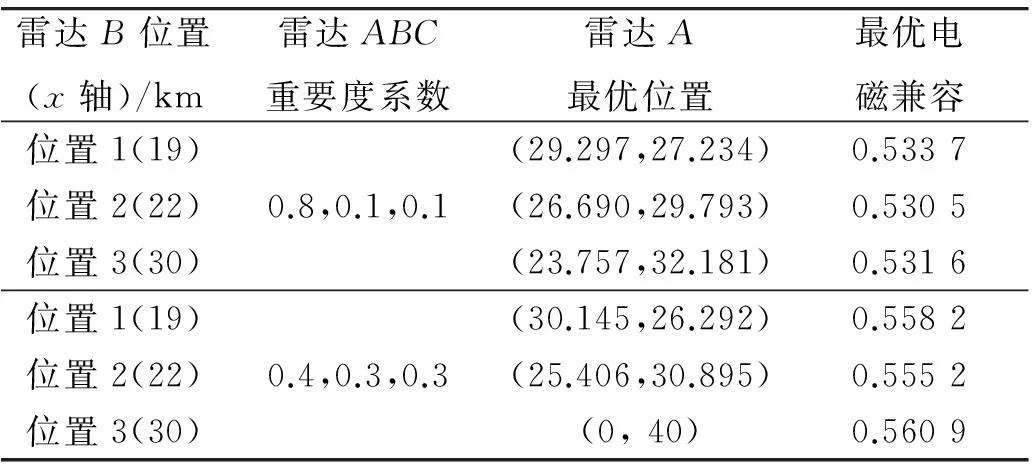
表2　雷达C位于y轴20 km处时位置优化结果

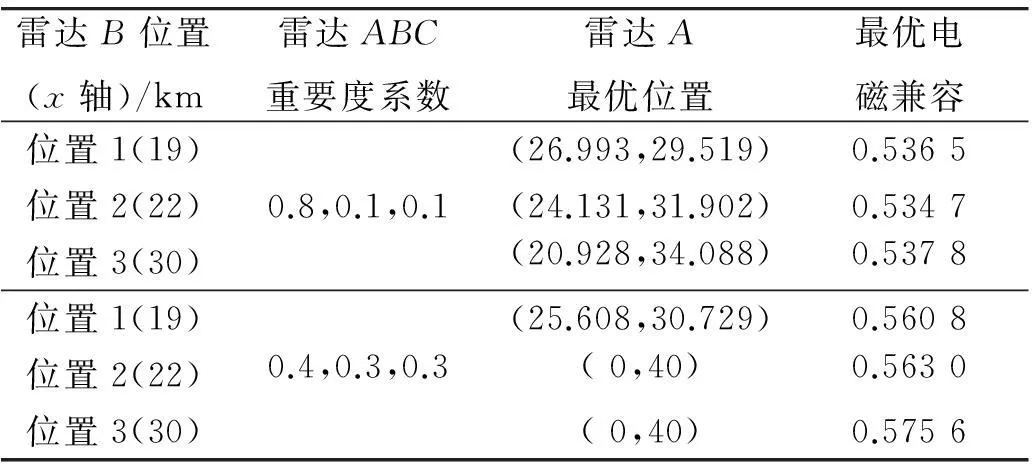
表3　雷达C位于y轴18 km处时位置优化结果

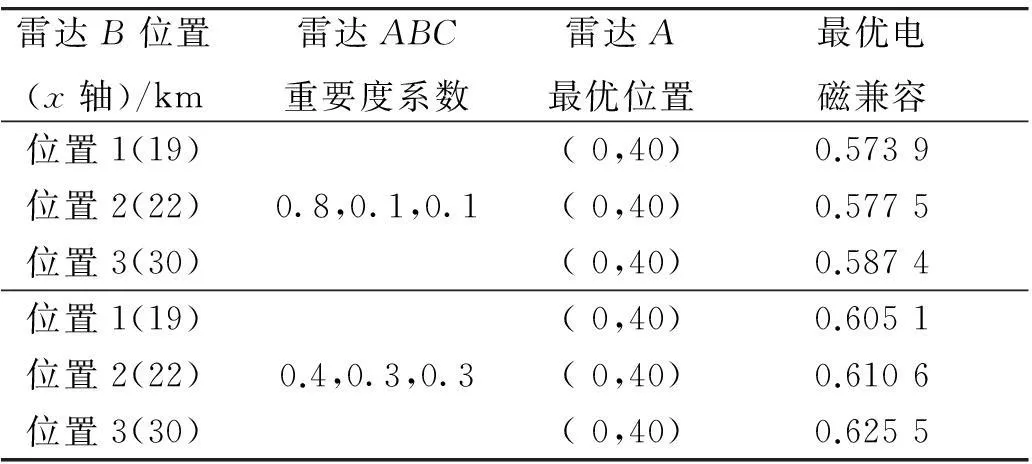
表4　雷达C位于y轴10 km处时位置优化结果

从上述表2～4可以看出，雷达的重要度系数对于雷达的电磁兼容程度有很重要的影响，当雷达A的重要度系数从0.8降低到0.4时，表2中总电磁兼容程度由0.53提高到0.55～0.56，表3中总电磁兼容程度由0.53提高到0.56～0.57，表4中总电磁兼容程度由0.57～0.58提高到0.60～0.62；雷达B，C的位置对于雷达的电磁兼容程度有很重要影响，由表2～4可以发现在重要度系数相同时，随着雷达B在x轴离原点距离的增大，总电磁兼容程度并不是线性增大的。例如在表2中第一次优化的结果中，位置1：Φ总=0.533 7；位置2：Φ总=0.530 5；位置3：Φ总=0.531 6。

从上述表2～4中的结果可以看出，雷达B，C的位置对最优的雷达A的位置也有很大影响，但是当雷达C位于y轴10 km时，雷达A的最优位置不发生改变，这时候最优位置超出了所要求的雷达位置范围。雷达的重要度系数也会影响雷达A的最优位置，例如表2中在雷达B位置相同时，雷达A的最优位置也明显不同。

上述仿真结果表明，应用粒子群算法结合电磁兼容模型，可以很好地解决频率相近或相同雷达工作时的优化部署问题。

4结束语

本文应用粒子群算法，提出了一种基于电磁兼容分析的雷达优化部署方法。针对由工作频率相近或相同的定向天线雷达和全向天线雷达组成雷达系统，建立了雷达的电磁兼容模型，将电磁兼容程度作为雷达位置优化部署的适应度函数，以满足作战要求为前提确定雷达的位置空间范围，运用粒子群算法对雷达的部署进行优化。仿真结果表明，在雷达频谱拥挤的情况下，该方法可以有效地解决雷达的优化部署问题，使得雷达在满足作战要求的范围内，电磁兼容程度达到最大，对舰船编队时决定舰船的位置有一定参考作用。

参考文献：

[1]毛滔,曾浩.雷达抗同频干扰方法研究[J].航天电子对抗，2005,21(6):43-45.

MAO Tao, ZENG Hao.Anti-Interference in the Same Frequency of Radar[J].Aerospace Electronic Warfare,2005,21(6):43-45.

[2]郎维川,张林昌,楼鼎夫,等.GB/T17624.1-1998 电磁兼容综述电磁兼容基本术语和定义的应用与解释[S].北京:中国标准出版社,1998.

LANG Wei-chuan,ZHANG Lin-chang,LOU Ding-fu,et al. Electromagnetic compatibility-General-Application and Interpretation of Fundamental Definitions and Terms[S].Beijing:Standards Press of China,1998.

[3]邱炎,肖雳.电磁兼容标准与认证[M].北京:北京邮电大学出版社,2002.

QIU Yan,XIAO li.Electromagnetic Compatibility Standards and Certification[M].Beijing:Beijing University of Posts and Telecommunications Press,2002.

[4]邢福成,康锡章.雷达组网区域性防御区优化部署[J].现代防御技术,2004,32(4):58-62.

XING Fu-cheng,KANG Xi-zhang.The Optimal Deployment of Radar Network in a Defensive Area[J].Modern Defense Technology,2004,32(4):58-62.

[5]蔡婧,许剑,李婧娇.基于文化遗传算法的雷达优化部署[J].现代防御技术,2010,38(6):6-11.

CAI Jing,XU Jian,LI Jing-jiao.Genetic Algorithm Based on Optimal Deployment of Radar Network[J].Modern Defense Technology,2010,38(6):6-11.

[6]刘彦君,黄金才,王江.有源干扰条件下基于NSGA-Ⅱ的雷达网优化部署方法[J].指挥控制与仿真,2014,36(1):36-40.

LIU Yan-jun,HUANG Jin-cai,WANG Jiang.Optimal Deployment of Radar Network Based on NSGA-Ⅱ Under Active Jamming[J].Command Control & Simulation,2014,36(1):36-40.

[7]崔玉娟,察豪,田斌.改进的混合蛙跳算法在雷达网部署中的应用[J].海军工程大学学报,2015,36(1):36-40.

CUI Yu-juan,CHA Hao,TIAN Bin.Improved Shuffled Frog Leaping Algorithm for Radar Network Deployment[J].Journal of Naval University of Engineering,2015,36(1):36-40.

[8]谭贤四,武文,王红,等. 区域警戒雷达网优化部署研究[J].现代雷达,2001,23(5):6-10.

TAN Xian-si,WU Wen,WANG Hong,et al.Study on Optimizing a Locally Netted Warning Radar System[J].Modern Radar,2001,23(5):6-10.

[9]孙国伟,谢军伟,孙博.一种新的组网雷达优化布站方法[J].计算机仿真,2013,30(9):23-26.

SUN Guo-wei,XIE Jun-wei,SUN Bo.New Method of Network Radar Optimized Disposition[J].Computer Simulation,2013,30(9):23-26.

[10]师俊朋,胡国平.基于N-P准则的雷达网反隐身探测概率分析[J].现代防御技术,2015,43(2):24-28.

SHI Jun-peng,HU Guo-ping.Performance Research of Radar Network Anti-Stealth Detection Probability on N-P Criterion[J].Modern Defense Technology,2015,43(2):24-28.

[11]MAHAFZA B R,ELSHERBENI A.MATLAB Simulations for Radar Systems Design[M].Chapman&Hall/CRC Press,2003.

[12]李圭源,张厚,殷雄,等.基于作用距离衰减的雷达间电磁兼容模型[J].电讯技术,2010,50(3):49-53.

LI Gui-yuan,ZHANG Hou,YIN Xiong,et al.Radar Electromagnetic Compatibility Model Based on Radar Range Attenuation[J].Telecommunications Technology,2010，50(3):49-53.

[13]史豪杰,邢清华,刘付显.基于最大作用距离损耗的雷达间电磁兼容度量新方法[J].现代防御技术,2010,38(6):138-140.

SHI Hao-jie,XING Qing-hua,LIU Fu-xian.A New Method to Measure EMC between Radars Based on Maximun Radar Range’s Loss[J].Modern Defense Technology,2010,38(6):138-140.

[14]侯民胜.雷达之间的干扰及概率计算[J].雷达与对抗,2006,26(2):16-18.

HOU Min-sheng.The Analysis of Interference Between Radars and the Computation of Interference Probability[J].Radar and ECM,2006,26(2):16-18.

[15]KENNEDY J,EBERHART R C.Particle Swarm Optimization [C]∥Proceedings of International Conference on Neural Networks.New York: IEEE,1995:1942-1948.

[16]EBERHART R C,SHI Y H.Particle Swarm Optimization:Development,Applications and Resources[C]∥Proceedings of the Congress on Evolutionary Computation. Piscataway:IEEE,2001:81-86.

Ship-borne Radar Optimal Deployment Method Based on EMC Analysis

FANG Xiao-xing,ZHU Zhi-yu,ZHANG Bing,LI Yang

(Jiangsu University of Science and Technology,Dept. of Electronics and Information,Jiangsu Zhenjiang 212003,China)

Abstract:Aimed at the existence of electro-magnetic compatibility (EMC) problems between similar or identical frequency radars when ship-borne radar spectrum is crowding, a radar optimal deployment method based on EMC analysis is presented. For the radar systems composed of directional antenna radars and omni-directional antenna radars, an EMC degree measurement model is established as the fitness function. The optimal deployment of the radars can be got with particle swarm optimization (PSO) algorithm. The simulation results show that application of PSO algorithm combined with EMC model can commendably solve the radar optimal deployment problems.

Key words:electro magnetic compatibility(EMC); radar antenna; measurement model;ship-borne radar system; particle swarm optimization(PSO);optimal deployment

*收稿日期：2015-04-20；修回日期：2016-06-06

基金项目：船舶预研支撑技术基金项目(13J3.3.5);江苏省普通高校研究生科研创新计划资助项目(KYL X15_1109)

作者简介：方小星(1991-)，男，江苏江都人。硕士生，主要研究方向为电磁兼容分析。

通信地址：212003江苏省镇江市梦溪路2号江苏科技大学电子信息学院E-mail：fang_xiaoxing@126.com

doi:10.3969/j.issn.1009-086x.2016.02.006

中图分类号：TN956

文献标志码：A

文章编号：1009-086X(2016)-02-0037-06

空天防御体系与武器