基于凸优化的有限推力远程转移轨迹优化*

李 鑫 欧阳高翔 孙成明 孙 铮 杨 新

1. 中国科学院光电研究院，北京100094 2. 中国科学院大学, 北京 100049



基于凸优化的有限推力远程转移轨迹优化*

李 鑫1,2欧阳高翔1孙成明1孙 铮1杨 新1

1. 中国科学院光电研究院，北京100094 2. 中国科学院大学, 北京 100049

针对轨迹优化问题中动力学方程对凸优化方法的限制，建立了有限推力远程转移轨迹优化问题的凸优化问题模型，并提出一种迭代逼近算法，使得在每步迭代中状态矩阵保持为线性，从而实现了凸优化在远程轨迹优化中的应用，仿真分析证明了所提出的迭代逼近算法对优化问题的收敛性，所得轨迹迅速收敛至最优轨迹，并与最优控制序列所得实际轨迹保持一致。本文构建的凸优化问题模型及提出的迭代逼近算法对这类远程轨迹优化问题是可行的。

凸优化；远程转移；有限推力；轨迹优化；迭代逼近

航天器燃料最优的转移问题一直是研究的热点，广泛存在于交会对接、机动变轨、行星际航行等工程应用中。国内外学者对有限连续推力航天器轨道转移问题的研究主要有2类方法。Yan Hui等人使用基于初始协态变量猜测的间接法研究了最优轨道转移问题[1]，其本质是求解一个非线性方程组，其结果的最优性得到理论保证，但采用间接法需要对协状态变量的初值进行猜测，鲁棒性较差。王明春等人将两点边值问题的求解转化为非线性规划问题，以控制变量初始值代替伴随变量初始值，对轨道转移问题进行了求解[2]。但这种变换仍然无法解决间接法需要初值猜测的弊端。Johnson较早采用直接法对轨道转移问题进行了研究[3]，他运用Chebyshev多项式和积分惩罚函数将原始问题转化为无约束最优问题，从而能够数值求解。Enright和Conway利用直接配置和非线性规划方法处理了同平面有限推力转移最优轨迹问题[4]。采用直接法求解轨迹优化问题时，是将优化问题转化为非线性优化问题，采用非线性规划算法进行求解计算量大。张亚锋利用Guass伪谱法将最优控制问题转化为非线性规划问题，求解了有限推力的同面轨道和异面轨道的能量最优转移[5]。

近年来，凸优化理论及方法取得较大发展并被广泛应用。凸优化问题是非线性优化中非常重要的一种类型，这类问题的局部极小点就是全局最小点，因此如果凸优化问题的目标函数是一个严格凸函数，且存在极小点，那么它的极小点就是最小点，并且这个点是唯一的。以往研究的重点是区分线性与非线性，而凸优化只关注问题的凸与非凸。目前，凸优化已被应用于航天器交会最终逼近段轨迹优化以及行星大气再入轨迹优化等领域。Acikmese和Blackmore等将凸优化技术应用于火星登陆器软着陆最优控制问题[6-10]，将问题转化为二阶锥形式的凸优化问题，使用内点法求解。Liu Xinfu和Lu Ping等运用凸优化技术研究了交会对接中的轨迹优化问题[11-12]，针对约束条件研究了一种无损松弛方法，并验证了求解结果等价于原始问题。国内的林晓辉等人基于凸优化理论研究了月球定点着陆的轨迹优化[13]，池贤彬等人运用凸优化方法提出了有限推力下最终逼近段的自主交会迭代制导方法[14]，陈洪普将凸优化方法应用于高超声速飞行器再入制导中的模型预测控制[15]。

运用凸优化技术的前提是正确判别问题是否属于凸优化问题，以及按照DCP(Discplined Convex Programming)规则对问题进行正确合适的凸优化表述。由于凸优化理论和方法对等式约束要求为凸函数，而轨迹优化问题中动力学方程存在强非线性项，以往在近程轨迹优化问题的研究中往往将其进行简单的近似处理，文献[13-15]中均采用此类方法。但在应用至远程轨迹优化问题时如仍采用这类方法，不仅不符合客观实际，并且其计算结果的可靠性和准确性也无法保证。本文针对有限推力远程转移问题，构建了其凸优化问题模型，并提出迭代逼近算法，使得在求解凸优化问题时状态方程保持为线性，从而克服了凸优化方法应用于远程轨迹优化时在动力学方程非线性上的限制。通过仿真计算，验证了该方法的有效性、准确性和计算效率。

1 基于凸优化的问题建模

[16]中有限推力轨道拦截问题的数学模型类似，有限推力远程转移的燃料最优轨迹优化问题可以表述为：

(1)

1)航天器的推力形式为有限推力形式，存在推力上下界；在每个迭代周期内，认为质量为常量，推力矢量恒定。

2)上节所描述的问题模型中，在整个转移过程中航天器质量是线性时变的，但状态方程含有质量导数项为非凸函数。为此，对变量做如下变换：

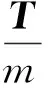
(2)

则质量方程可转化为：

(3)

3)推力约束方程所定义的集合为非凸集，通过引入松弛因子η，将控制输入约束方程二维空间中的非凸集约束转换为三维空间中的凸集约束，并使性能指标函数为线性函数形式：

(4)

4)对于推力大小约束方程0≤η≤Tmaxe-e，将其右端在z0进行一阶泰勒展开，并近似缩小为凸集约束：

0≤σ≤Tmaxe-z0[1-(z-z0)]

(5)

通过上述假设和变换，并令x=[rvz]T为状态变量，u=[τη]T为控制变量，同时考虑实际轨迹的具体约束，则原始问题模型转化为如式(6)所示的凸优化问题模型：

(6)

式中,

考虑J2摄动项，则Q(r)表示为：

Q(r)=

其中,J2=1.0826×10- 9，Rg=6378 km。

由于在凸优化方法中，一般不采用积分表达形式，因而对式(6)进行离散化处理，转化为矩阵相乘的形式。

(7)

式中，Tc为采样周期，状态转移矩阵Φ(t)=eA(r(n))t，对其进行幂级数展开并忽略高阶项可得Φ(t)=eA(r(n))t=I+At，从而可计

则离散化后，原凸优化问题转化为如下形式：

(8)

2 迭代逼近算法

本文研究的这类远程轨迹优化问题中，r变化范围大，A具有明显的时变特性和强非线性，这对问题有无可行解，以及对可行解的准确性都有重要影响。因而，本文研究并设计了一种迭代逼近算法，通过在每一步迭代中求解上一节建立的凸优化问题，获得一组最优轨迹序列，更新状态矩阵A,并在每一步迭代中保持其为定常矩阵。最优轨迹和时变矩阵A都收敛至误差允许范围内，即获得最终的求解结果。算法流程如图1所示。

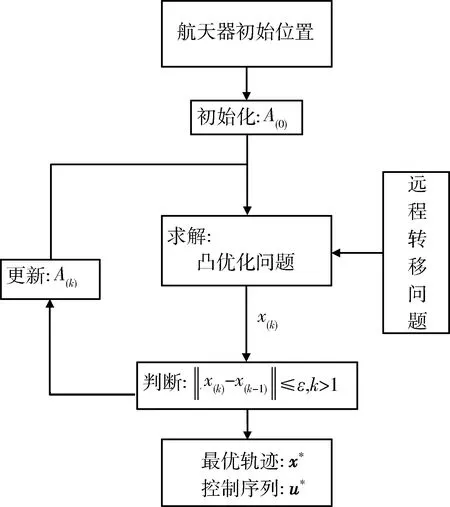
图1 迭代逼近算法流程

具体算法流程如下：

1)状态矩阵A的初始化

通过将初始位置与末端位置间的距离进行等分，得到一组猜测的初始位置序列，设置k=0 ，并对A进行初始化得到A(0)。通过后续验证，采用这种初始化方法，有效地保证了第1)步迭代能获得可行解，进而保证迭代算法的进行；

2)求解凸优化问题

在第u=u(k)步迭代中，以定常矩阵A(k)，求解上一节建立的凸优化问题式(8)，得到可行解x(k)和u(k)，分别为A(k)条件下的最优轨迹序列和控制序列；

3)终止判断

当迭代所得的轨迹收敛至误差允许范围内时，认为满足判断条件，即x(k)-x(k-1)≤ε,k>1，其中常值ε为允许误差，则最终结果x*=x(k)，u*=u(k)。如不满足判断条件，则进行下一步；

4)迭代更新A(k)

以第2)步获得的x(k)计算得矩阵A(k)，并返回到第2)步。

在此，对本文提出的迭代逼近算法的收敛性进行简要的证明如下：

根据文献[17]，若矩阵A(x)满足条件

A(x)-A(y)≤αx-y
μ(A(x))≤μ0

(9)

其中,α，μ0为正的常数，μ(A)为A的范数对数，则可以保证解序列{x(k)}的收敛性。

在本文研究的问题中，可令r被地球半径归一化，使得r>1，由矩阵二阶范数定义可得

(10)

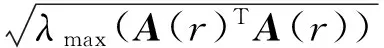
(11)

A(r1)-A(r2)≤A(r1)+A(r2)=2

(12)

并且

(13)

由文献[18-19]对矩阵的对数范数的定义及扩展可得

(14)

综上，证明了本文提出的迭代逼近算法对所研究的问题具有收敛性。

3 仿真分析

为了验证所提出的凸优化问题模型以及迭代逼近算法，针对有限推力下的远程轨道转移进行了仿真计算。转移过程以燃料最优为性能指标，同时考虑初末位置约束及推力大小约束。

航天器在地心惯性系下的初始位置及初始速度，以及转移目标点处的位置和速度如表1所示，其他仿真参数如表2所示。

表1 初始及目标状态

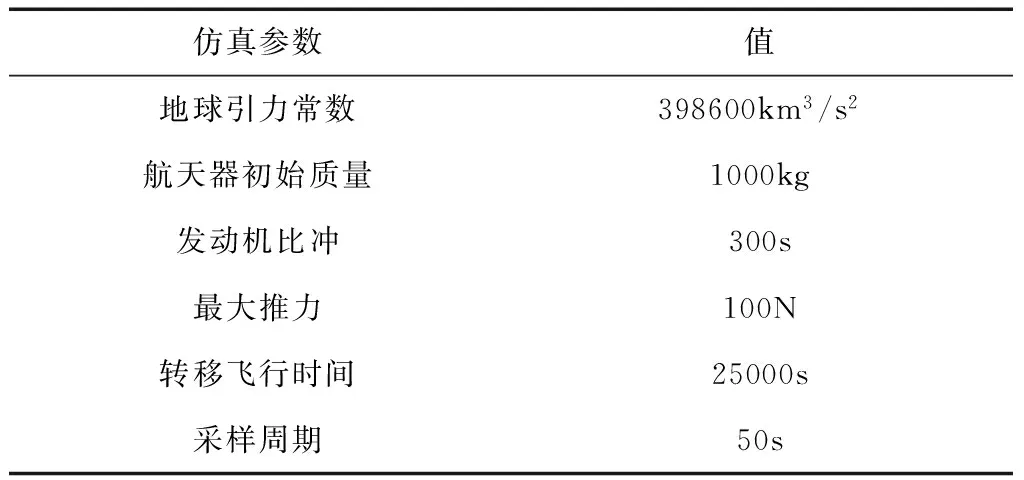
表2 仿真参数表

仿真结果见图2～6。图2为地心惯性系下的最终优化轨迹，可以看出航天器沿最优轨迹从初始位置到达目标位置，两点间距离71164km，轨道半径相差2164km，即实现了远程转移的任务要求。

图2 最终优化轨迹

图3为迭代过程中的推力幅值变化曲线。可以看出在迭代计算过程中，每一次计算得到的控制推力序列，其幅值满足推力大小约束，且近似在最大值与最小值之间切换。

图4为最终优化结果中航天器在X，Y方向上的位置及推力变化。可以看出，位置变化平缓稳定，X方向位置变化范围达61082km，Y方向位置变化范围达36515km；X，Y方向上的推力同图3所示推力幅值变化规律一致。

图3 迭代过程中的推力幅值变化

图4 XY位置变化及推力作用段

图5 燃料消耗收敛曲线

图5为迭代过程中优化目标即燃料消耗的收敛曲线。可以看出，通过最初的几步迭代，燃料消耗由424kg迅速下降至280kg附近，并最终收敛至276kg。与基于Lambert的双脉冲转移进行对比，见表3，可以看出基于本文方法所产生的速度增量已十分接近双脉冲转移。

表3 方法及结果对比

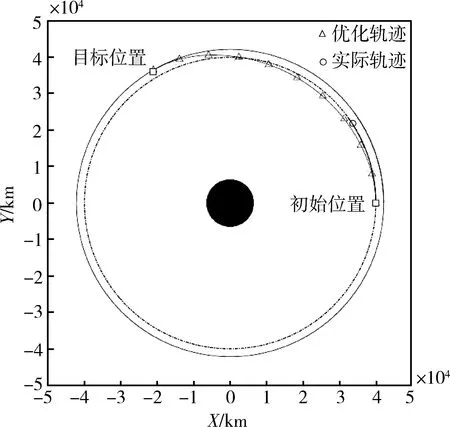
图6 优化轨迹与实际轨迹

本文提出的方法可同时求解出最优轨迹和最优控制序列，为了验证结果的准确性，进行误差分析，对优化所得的控制序列在航天器动力学方程下进行轨道外推，将所得轨迹与优化所得的最优轨迹进行对比，如图6所示。可以得出，最终位置误差为465km，仅为最终轨道半径的1.1%，优化结果与外推结果基本一致，证明了本文提出方法的有效性和准确性。

在Matlab编程环境及CPU频率为2.27GHz的硬件平台下，每步迭代计算中的凸优化求解耗时在1.24～3.23s之间。通过近500步迭代，由图6最终收敛段可见,计算结果已基本收敛至最优，说明了凸优化方法及迭代逼近算法的有效性和较高的计算效率。进行较长步数的迭代，可得到较高精度的最优轨迹和控制序列，保证优化轨迹与外推轨迹基本重合。

仿真结果表明：由于凸优化理论和方法对等式约束要求为凸函数，而轨迹优化问题中动力学方程存在强非线性项，以往在近程轨迹优化问题的研究中往往将其进行简单的近似处理，但在应用至远程轨迹优化问题时如仍采用这类方法，不但不符合客观实际，其计算结果的可靠性和准确性也无法保证。本文提出的方法准确求解了有限推力远程转移问题，转移距离达数万千米，而已有凸优化方法在轨迹优化领域的应用只局限于数百米，表明本文方法有效地解决了非线性状态方程对凸优化方法应用的制约问题。

基于本文方法能够同时求解出最优轨迹和最优控制序列。最优轨迹与按控制序列进行外推所得实际轨迹的误差在允许范围内，末端位置和速度均达到约束要求，证明了方法的准确性和高效性。

本文求解过程采用了斯坦福大学开发的CVX工具软件，按照其语法规则编写程序，在每一步迭代中求解了式(8)所示的凸优化问题。

4 结论

基于凸优化理论和方法，对航天器远程转移轨迹优化问题进行了建模和凸优化问题标准形式的表述。针对制约凸优化方法应用于远程轨迹优化的非线性状态方程，提出并设计了一种迭代逼近算法，并通过仿真计算证明了其有效性。其能有效求解远程转移轨迹优化问题。对将凸优化应用拓展至远距离的航天器远程转移、交会远程导引、远程制导等问题进行了有意义的探索。

参 考 文 献

[1] Yan H, Wu H Y. Initial Adjoint-Variable Guess Technique and Its Application in Optimal Orbital Transfer [J]. Journal of Guidance, Control, and Dynamics, 1999, 22(3):490-492.

[2] 王明春, 荆武兴, 等.能量最省有限推力同平面轨道转移 [J].宇航学报, 1992, 13(3):24-31. (Wang Mingchun, Jing Wuxing, et al. Minemum Fuel Orbit Coplanar Transfers with Finite Thrust [J]. Journal of Astronautics, 1992, 13(3):24-31.)

[3] Johnson F T. Approximate Finite-thrust Trajectory Optimization [J]. AIAA Journal, 1969, 7(6):993-997.

[4] Enright P J, Conway B A. Optimal Finite-thrust Spacecraft Trajectories Using Collocation and Nonlinear Programming [J]. Journal of Guidance, Control, and Dynamics, 1991, 14(5):981-985.

[5] 张亚锋, 和兴锁. 基于Guass伪谱法的有限推力轨道转移优化 [J].航天控制, 2010, 28(3):38-41. (Zhang Yafeng, He Xingsuo. Optimal Orbit Transfer with Finite Thrust Based on Guass Pseudospectral Method [J]. Aerospace Control, 2010, 28(3) :38-41.)

[6] Acikmese B, Scott R P. Convex Programming Approach to Powered Descent Guidance for Mars Landing [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5):1353-1366.

[7] Acikmese B, Blackmore L. Enhancements on the Convex Programming Based Powered Descent Guidance Algorithm for Mars Landing [C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, 2008.

[8] Blackmore L, Acikmese B, et al. Minimum Landing error Powered Descent Guidance for Mars Landing Using Convex Optimization [J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4):1161-1172.

[9] Acikmese B, John M, et al. Lossless Convexification of Nonconvex Control Bound and Pointing Constraints of the Soft Landing Optimal Control Problem [J]. IEEE Transactions on Control System Technology, 2013, 21(6):2104-2113.

[10] Blackmore L, Acikmese B, et al. Lossless Convexification of Control Constraints for a Class of Nonlinear Optimal Control Problem [J]. Systems&Control Letters, 2012, 61(8):863-870.

[11] Liu Xinfu, Lu Ping. Solving nonconvex optimal control problems by convex optimization [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3):750-765.

[12] Lu Ping, Liu Xinfu. Autonomous Trajectory Planning for Rendezvous and Proximity Operations by Conic Optimization [J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3):750-765.

[13] 林晓辉, 于文进.基于凸优化理论的含约束月球定点着陆轨道优化 [J].宇航学报, 2013, 34(7):901-908. (Lin Xiaohui, Yu Wenjin. Constrained Trajectory Optimization for Lunar Pin-point Landing Based on Convex Optimization Theory [J]. Journal of Astronautics, 2013, 34(7):901-908.)

[14] 池贤彬, 岳晓奎, 等. 基于凸优化的自主交会迭代制导方法 [J].中国空间科学技术, 2014, 1:26-34. (Chi Xianbin, Yue Xiaokui, et al. Iterative Guidance Method of Autonomous Rendezvous Based on Convex Optimization [J]. Chinise Space Science and Technology, 2014, 1:26-34.)

[15] 陈洪普.基于凸优化的模型预测控制在飞行器再入制导中的应用 [D].哈尔滨:哈尔滨工业大学, 2013.(Chen Hongpu. The Application of Convex Optimization Based Model Predictive Control in Guidance of Reentry Vehicles [D]. Harbin:Harbin Institude of Technology, 2013.)

[16] 汤一华, 陈士橹, 等.基于遗传算法的有限推力轨道拦截优化研究 [J].西北工业大学学报, 2005, 23(5):671-675.(Tang Yihua, Chen Shilu, et al. A Genetic Algorithm Method of Orbit Interception with Finite Thrust [J]. Journal of Northwestern Polytechnical University, 2005, 23(5):671-675.)

[17] Banks S P, Dinesh K. Approximate Optimal Control and Stability of Nonlinear Finite and Infinite-dimensional Systems [J]. Annals of Operations Research, 2000,98:19-44.

[18] Ström T. Logarithmic norms [J]. SIAM Journal of Numercial Analysis, 1975, 12(5):741-753.

[19] Ström T. Minimization of Norms and Logarithmic Norms by Diagonal Similarities[J]. Computing, 1972,10:1-7.

Optimal Remote Transfer with Finite Thrust Based on Convex Optimization

Li Xin1,2，Ouyang Gaoxiang1，Sun Chengming1，Sun Zheng1，Yang Xin1

1. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China 2. University of Chinese Academy of Sciences, Beijing 100049, China

Aimingatthelimitationofthekineticequationagainstconvexoptimizationapplicationintheremotetransfertrajectory,theconvexoptimizationmodelofremotetransfertrajectoryoptimizationwithfinitethrustisestablished,andaniterativeapproximationalgorithmisproposedtokeepthestatematrixlinearineachiteration,thereby,theconvexoptimizationcansolvetheproblemsmoothly.Itisproventhattheconvergenceofproposediterativeapproximationalgorithmfortheoptimizationproblemandtheoptimaltrajectoryandcontrollawaresimultaneouslysolved.Throughanalysisandverification,theresultingoptimalcontrollawisinaccordwiththeoptimalcontrolsequences,meanwhile,theresultingoptimaltrajectoryandactualtrajectoryareconsistent.Theconvexoptimizationmodelestablishedandtheiterativeapproximationalgorithmproposedarevaluableandfeasiblefortheremotetrajectoryoptimization.

Convexoptimization;Remotetransfer;Trajectoryoptimization;Finitethrust;Iterativeapproximationalgorithm

*国家自然科学基金(61308101)

2015-08-03

李 鑫(1990-)，男，山西大同人，硕士，主要研究方向为飞行器设计，航天器轨迹优化；欧阳高翔(1977-)，男，四川人，博士，高级工程师，主要研究方向为飞行器设计，飞行器轨道姿态控制及仿真；孙成明(1984-)，男，吉林人，博士，助理研究员，主要研究方向为空间目标光学探测与识别；孙 铮(1985-)，男，北京人，硕士，工程师，主要研究方向为空间应用系统总体设计；杨 新(1967-)，男，北京人，博士，研究员，主要研究领域为空间应用系统总体设计、空间飞行器总体设计。

V412.41

A

1006-3242(2016)03-0019-07