火箭TVC伺服系统频率特性测试算法研究

钱昌年 姜晨维 傅俊勇

1.上海航天控制技术研究所，上海2011092.上海市伺服系统工程技术研究中心，上海201109



火箭TVC伺服系统频率特性测试算法研究

钱昌年1,2姜晨维1,2傅俊勇1,2

1.上海航天控制技术研究所，上海2011092.上海市伺服系统工程技术研究中心，上海201109

总结归纳了火箭TVC(Thrust Vector Control)伺服系统常用频率特性测试方法的原理和特点，发现了相关分析法和传统最小二乘拟合法的等价性质。提出一种改进的最小二乘拟合法，通过引入高次项使算法具有了对复杂漂移干扰的处理能力。定义了算法的评价准则，使用数值仿真分析了4种测试算法的性能，得出了不同算法在不同场合的适用性结论，仿真结果表明在复杂漂移干扰下本文提出的新算法精度高于其他3种传统算法。

TVC伺服系统；频率特性；相关分析法；最小二乘拟合法

火箭伺服系统是火箭推力矢量控制(TVC)伺服系统的简称，是火箭姿态控制系统的子系统，负责调整火箭发动机喷管的摆角。其频率特性是重要的考核指标，运载火箭伺服系统普遍使用正弦逐点扫描法(简称扫频法)测试频率特性。从扫频数据求取频率特性，常见的方法有FFT计算法、相关分析法(COR)、功率谱法(PSD)和最小二乘拟合法(LSQ)等[1-5]。对于实际伺服系统，扫频数据除受噪声影响外，还受结构谐振及其他因素引入的数据漂移影响，严重的数据畸变给频率特性的求取带来了困难。文献中对上述算法的研究多关注于算法的应用，对算法的适用性、鲁棒性及准确性少有研究[6-7]。本文对FFT计算法、相关分析法、功率谱法和最小二乘拟合法的原理和实现方法进行分析和总结，并提出了一种精度更高的处理方法。

1 问题背景

以某型伺服系统为例，当输入正弦信号频率为14.32Hz、幅值为0.4°时，输出信号如图1所示，信号频谱如图2所示。输出信号受噪声影响严重；漂移特性复杂，其影响难以靠简单方法去除；谐振影响明显，位于30Hz的谐振频率成分量级较大且位置接近扫频试验的最高频率25Hz，对试验结果的影响不可忽略。经过滤波、去除均值和去除趋势处理后，依然不能有效消除该信号畸变(如图3)，在某些开环扫频场合，漂移干扰更加复杂。

由于各种原因，测试得到的数据可能存在频率成分不单一，分布不均匀且不够平滑的问题，故有必要研究不同频率特性计算方法的适用性，或改进现有计算方法，提高对复杂干扰的处理能力。

图1 伺服系统扫频信号(14.32Hz)

图2 伺服系统扫频信号频谱(14.32Hz)

图3 经过预处理的伺服系统扫频信号(14.32Hz)

2 频率特性测试方法

2.1 FFT计算法

使用FFT算法分别计算输入和输出信号的频谱，对频谱的幅值求商，相位求差，就可以得到系统的频率特性。

离散输入序列傅里叶变换表示为XFFT(k)，k=0,1,…,L-1，设输出信号的FFT结果为YFFT(k)，则系统的频率特性可以写为

(1)

其中，round(·)表示四舍五入取整；Fs为采样频率；2πFs/L表示频谱的频率分辨率(rad/s)。

通常情况下感兴趣的频率点ω不是2πFs/L的整数倍，当2πFs/L较大时，由式(1)近似处理带来的误差较大。

2.2 相关分析法

设输入信号为x(t)=Axsin(ωt)，则线性系统的输出信号可以表示为

(2)

要计算系统在ω的频率特性只需求得基波成分的幅值和相位即可。将式(2)展开，得到

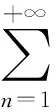
(3)其中,an=Ancosθn，bn=Ansinθn。 分别计算y(t)与sin(ωt)，cos(ωt)的互相关函数P，Q(时间差为0)

(4)

(5)

其中，N为正整数，表示进行积分的基波周期个数；T为基波周期。P和Q也可以视为输出信号y(t)的傅里叶级数中基波成分的系数。

根据式(4)和(5)可以解得

(6)

(7)

将该方法应用于离散信号，设系统输入信号为x(n)，输出信号为y(n)，其中n=0,1,2,…,L-1，数据采样周期为Ts。将式(4)和(5)中的积分运算替换为求和运算，得到

(8)

(9)

其中,tn=nTs。该方法运算量较小，在频率特性测试软件中应用广泛[2-3]。

2.3 功率谱法

设输入输出信号分别为序列x(n)，y(n)，n=0,1,2,…,L-1，是各态遍历的宽平稳随机信号，且均值为0。输入信号的自功率谱和输入输出信号的互功率谱分别为

(10)

(11)

其中，“*”表示复共轭。根据式(10)和(11)解出系统的频率特性

(12)

在上述推导过程中使用了宽平稳各态遍历且均值为0的假设，但工程实践证明该方法对信号的适应性较强，可以适用于白噪声、正弦逐点扫描信号、Chirp信号和Multitone信号等。工程上常使用周期图法和welch法等计算信号功率谱[8]，在精度要求不高的场合可以作为一种快速算法。

2.4 最小二乘拟合法及其改进

设系统的输入信号为序列x(n)=Axsin(ωnTs)，n=0,1,2,…,L-1，其中Ts为采样周期。在传统最小二乘法中假设输出信号为

y(n)=Aysin(ωnTs+θ)
=Aysin(ωnTs)cosθ+Aycos(ωnTs)sinθ
=φn·K′

(13)

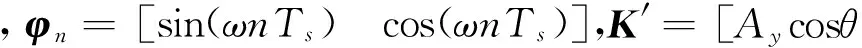
基于此输出形式，使用最小二乘方法求解未知参数矩阵K′，进一步即可求解输出信号的幅值Ay和相位θ，这是传统最小二乘法的思路。

可见，传统最小二乘法将输出信号作为理想信号处理，忽略了实际信号中可能存在的噪声、漂移和谐振干扰，用于处理图1信号的精度有待验证。

为了提高最小二乘拟合法对复杂信号的处理能力，可以对传统方法进行改进，在输出方程中增加关于时间的高次项，用于拟合复杂漂移，将干扰从实际信号中分离出来，使输出信号的幅值和相位求取免受干扰影响。系统输出可以表示为

y(n)=k0+k1nTs+k2(nTs)2+…+
kN′(nTs)N′+Aysin(ωnTs+θ)
=k0+k1nTs+k2(nTs)2+…+
kN′(nTs)N′+Aysin(ωnTs)cosθ+
Aycos(ωnTs)sinθ

(14)

其中，N′表示漂移干扰的最高阶次。将nTs用tn代替，将式(14)写成矩阵形式，得到

y(n)=φn·K

(15)

其中，

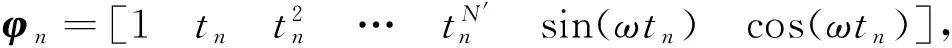
定义输出矩阵

其中，L为输入输出序列的长度。定义输入矩阵

(16)

则存在关系式

Y=Φ·K

(17)

式(17)的最小二乘解为

K=(ΦTΦ)-1ΦTY

(18)

若求出K，可进一步求出Ay与θ，则系统频率为ω时的频率特性可以表示为

(19)

工程上一般认为最小二乘法的处理精度最高[1]，上述拟合方法对传统最小二乘拟合方法进行了改进，既具有传统最小二乘方法对噪声和谐振干扰鲁棒性强的优点，而且能处理具有复杂漂移特性的信号，该方法的处理效果将在后续部分验证。

2.5 最小二乘拟合法与相关分析法的联系

当不考虑输出信号的复杂漂移干扰时，即采用传统最小二乘拟合法求取系统的频率特性，参数向量为

(20)

对应于N个周期输出数据的输出矩阵为

(21)

其中,L=NT/Ts。 根据式(18)，最小二乘解可以写为

(22)

应用三角函数正交性，将上式进一步化简得到

(23)

将式(23)与(8)和(9)对比发现

(24)

即传统最小二乘法的计算结果与相关分析法计算结果仅相差一个比例常数，由2种方法计算得到的频率特性是一致的。可以得出传统最小二乘拟合法在数据长度为整数个周期时与相关分析法等价。

3 处理方法对比

为客观比较几种方法的处理效果，应建立统一评价准则对处理方法进行验证。首先对比FFT、相关分析法(COR)、功率谱法(PSD)、传统最小二乘法(LSQ)和改进最小二乘法(LSQ2)的处理结果，接着使用传统最小二乘法和改进后的方法处理图1中数据，证明改进方法的有效性。

图4 仿真信号生成原理

3.1 评价标准

构造一组正弦逐点扫描信号x(n)，该信号由一组频率递增的正弦波组成，正弦波的频率为{ω1,ω2,…,ωNp}，NP为频率点的数量。如图4所示，x(n)通过一个二阶系统(ω0=62.8rad/s，ξ=0.25)，分别加入噪声干扰r(n)、谐振干扰w(n)和漂移干扰f(n)，得到具有确定幅值衰减和相位滞后的输出信号y(n)，理想二阶系统的频率特性表示为G0(jω)。

(25)

定义偏差向量

(26)

定义以下评价标准

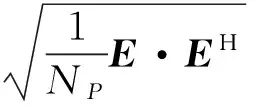
(27)

M=max(Ek),k=1,2,…,Np

(28)

其中，V用来衡量整体偏差，M用于衡量偏差的最大程度，数值越大表示偏差越明显。

3.2 特性分析

输入信号的幅值为1，正弦波的频率为{1Hz,2Hz,…,20Hz}，采样周期Ts=0.002s，使用Matlab/m语言编写代码来求取系统的频率特性。

图5 受噪声干扰时的处理误差

3.2.1 噪声干扰抑制能力

当输出信号仅受噪声干扰时(噪声呈正态分布，均值为0，标准差为0.12)，计算5种方法的处理结果与理想特性的偏差，如图5所示，FFT方法的误差较明显，在10Hz之后偏差较大；功率谱法在高频段也有较大误差。评价指标见表1和2，FFT方法的处理精度明显差于其他4种方法。

3.2.2 谐振干扰抑制能力

伺服系统在运行过程中，发动机部件或测量结构部件的结构谐振会干扰输出结果，如果谐振频率在扫频信号的频率范围之内，则其对测量精度的影响不可忽略。在数据中加入12Hz的正弦干扰，对应于每个扫频点的干扰信号幅值为

(29)

其中，fk=1Hz,2Hz,…,20Hz。即越靠近12Hz，谐振干扰的量级越大。处理结果如图6所示，评价指标见表1和2，FFT计算法处理结果与精确特性的偏差较大，功率谱法的计算精度也不理想，其余3种方法对谐振干扰的抑制能力较强。

图6 受谐振干扰时的处理误差(图例同图5)

表1 整体偏差V比较

干扰FFTCORPSDLSQLSQ2噪声0.09330.04480.05380.04430.0416谐振0.17570.05220.05530.05180.0465漂移0.77360.06340.23450.06030.0413

表2 最大偏差M比较

3.2.3 复杂漂移干扰抑制

在实际测试过程中，测试信号可能受到各种复杂因素引起的漂移干扰，扫频信号中加入均值为0的干扰

f(n)=e(3nTs/NT)-E(e(3nTs/NT))

(30)

其中，N为扫频信号周期数量；T为扫频信号周期；E(·)为求平均函数。式(30)用于模拟图1中的漂移干扰，即信号整体随时间不同程度偏移零位。5种方法的处理结果如图7所示，评价指标见表1和2，FFT计算法的相位偏差达到40°，功率谱法的最大相位偏差接近20°，已没有参考价值。通过评价指标可以看到改进后的最小二乘拟合法在处理漂移干扰方面的能力要强于传统最小二乘法和相关分析法，具有最高处理精度。

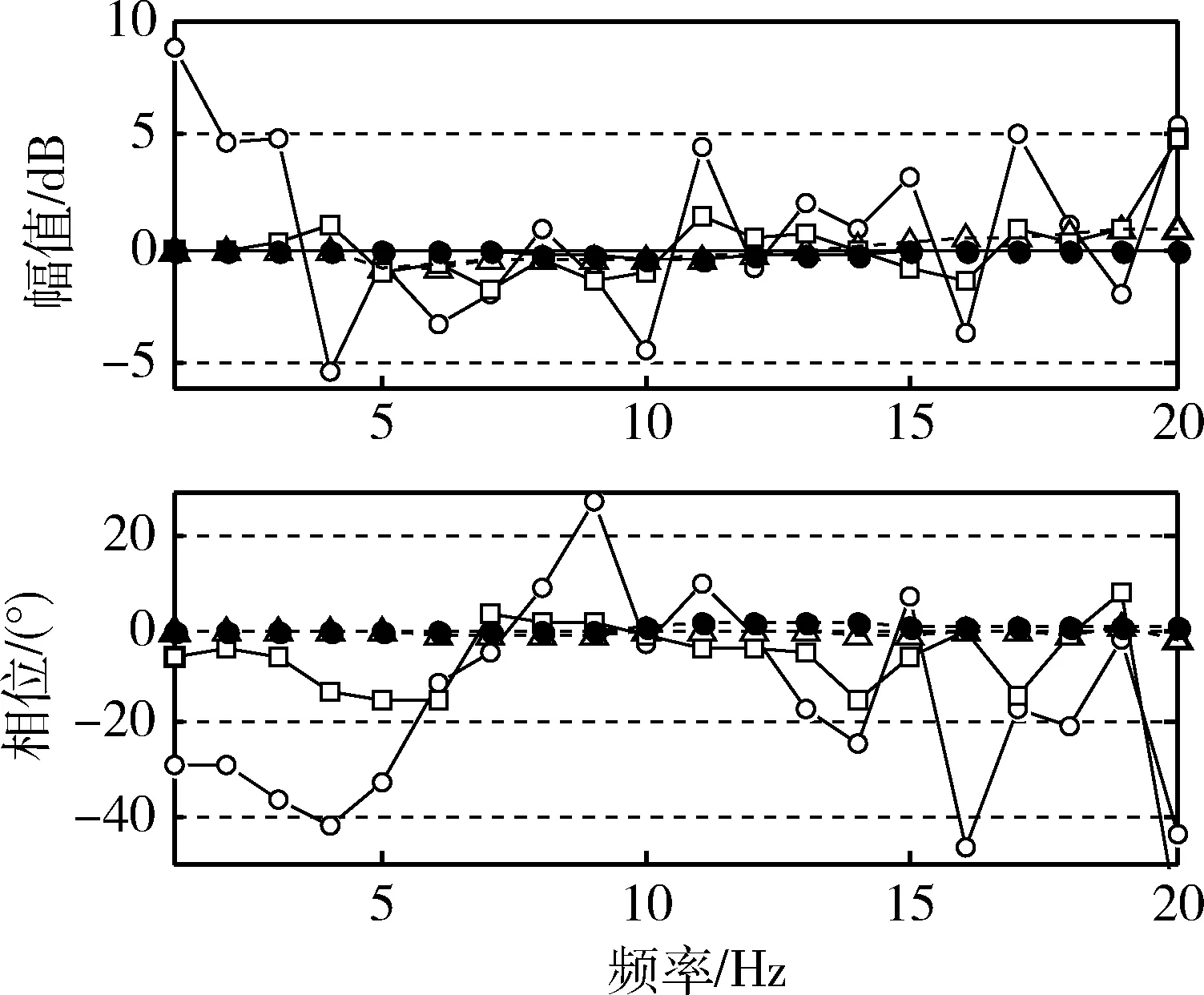
图7 受漂移干扰时的处理误差(图例同图5)

4 实际信号分析

根据以上仿真结果，FFT方法和功率谱法在干扰较严重时不宜使用，而改进后的最小二乘法具有最高精度。现在以图1数据为例，检验相关分析法、传统最小二乘法和改进方法应用于实际系统的处理效果，处理结果见表3。 对于图1所示14.32Hz信号，改进后的最小二乘法将频响幅值处理精度提高0.72dB，相位处理精度提高0.1°。

表3 实际数据处理结果

5 结论

通过推导4种频率特性测试算法的原理，发现了相关分析法和传统最小二乘法的等价性质。针对工程实际中扫频信号畸变严重的情况，提出了一种新的处理方法，有效排除了信号中漂移干扰的影响。通过仿真证明了在大漂移干扰下，新算法的精度高于其他常规方法。

[1] 侯国屏, 吴静, 董甲瑞. Multitone信号及其在测量中的应用[J]. 清华大学学报, 2007, 47(10): 1574-1577.(Hou Guoping, Wu Jing, Dong Jiarui. Multitone Signals and Its Applications in Measurement [J]. Journal of Tsinghua University (Sci&Tech), 2007, 47(10): 1574-1577.)

[2] Stroud C, Yang D Y， Dai F. Analog Frequency Response Measurement in Mixed-Signal Systems [J]. IEEE International Symposium on Circuits and Systems, Island of Kos, Greece, May 21-24, 2006.

[3] Miao B T, Zane R, Maksimovic D. System Identification of Power Converters with Digital Control Through Cross-Correlation Methods [J]. IEEE Journals & Magazines, 2005, 20(5): 1093-1099.

[4] 沈伟, 兰山. 伺服系统频率特性测试方法研究[J]. 试验技术与管理, 2011, 28(11): 268-271.(Shen Wei, Lan Shan. Research on Testing Method of Frequency Characteristic for Servo System [J]. Experimental Technology and Management, 2011, 28(11): 268-271.)

[5] 杨超. 现代运动控制系统的数字式频响测试方法[J]. 计算机测量与控制, 2006, 14(11): 1452-1455.(Yang Chao. Digital Frequency Response Test Method of Modern Motion Control System [J]. Computer Measurement & Control, 2006, 14(11): 1452-1455.)

[6] 汪首坤, 王军政. 基于调频脉冲扫频的导弹舵机频率特性测试方法[J]. 北京理工大学学报, 2006, 26(8): 697-703.(Wang Shoukun, Wang Junzheng. Frequency Response Testing Method for Missile Actuator Based on Frequency Modulated Pulse Sweep [J]. Transactions of Beijing Institute of Technology, 2006, 26(8): 697-703.)

[7] 支超有, 李振水, 李霞. 基于VXI总线的多通道频率响应测量与系统建模[J]. 测控技术, 2004, 23(1): 11-13.(Zhi Chaoyou, Li Zhenshui, Li Xia. Multi-Channel Frequency Response Measurement and Establishing System Model Based On VXI Bus [J]. Measurement & Control Technology, 2004, 23(1): 11-13.)

[8] 刘党辉, 蔡远文. 系统辨识方法及应用[M]. 国防工业出版社, 2010: 73-90.

Research on Frequency Response Detecting Algorithms for Launch Vehicle Servo System

Qian Changnian1,2, Jiang Chenwei1,2, Fu Junyong1,2

1. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China 2. Shanghai Engineering Research Center of Servo Systems, Shanghai 201109, China

Thegeneralalgorithmsfordetectingfrequencyresponseforlaunchvehiclethrustvectorcontrol(TVC)servosystemaresummarizedandanalyzed,andtheequivalencerelationshipbetweentraditionalleastsquarequadratic(LSQ)algorithmandcorrelation(COR)algorithmisdemonstrated.AnovelalgorithmbasedonLSQmethodisthenpresented,andinwhich,highordertermsareintroducedtoprocessthedriftinterference.Theeffectivenessofthealgorithmproposedisdemonstratedbysimulation.

TVCservosystem;Frequencyresponse; COR; LSQ

2015-06-18

钱昌年(1987-),男，甘肃武威人，硕士，工程师，主要从事火箭伺服系统控制研究；姜晨维(1987-),男，上海人，硕士，工程师，主要从事火箭伺服系统控制研究；傅俊勇(1972-)，男，江苏盐城人，硕士，研究员，主要从事火箭伺服技术研究。

V475.1

A

1006-3242(2016)03-0014-05