地下连续墙对地铁车站主体结构内力计算的影响
李玉琼
(深圳市地铁集团有限公司,广东深圳 518000)
地下连续墙对地铁车站主体结构内力计算的影响
李玉琼
(深圳市地铁集团有限公司,广东深圳 518000)
【摘要】以实际明挖车站工程为背景,通过有限元软件,分别计算车站主体结构在有无围护结构(地下连续墙)情况下的结构内力,并进行比较分析。本次建模计算分别采用SAP84与ANSYS有限元软件,通过两个软件的计算对比,发现有无围护结构对侧墙的内力影响十分明显,特别是侧墙中部。总的来说无围护结构方案计算过程简便,内力曲线更加连续合理,对地铁车站设计具有一定的指导意义。
【关键词】地下连续墙;重合墙结构;有限元
近年来,随着地铁建设的迅猛发展,连续墙在地铁车站围护结构设计中的应用愈来愈广泛。在地铁设计中,连续墙作为围护结构,与主体结构共同承受结构荷载,因此,其对结构受力有着极为关键的作用。本文以有限元软件为基础,结合某实际地铁工程,比较分析地下连续墙作为围护结构(重合墙结构),对车站主体结构内力计算的影响。
1工程概况
某市地铁2号线某车站有效站台中心里程处底板底部埋深为17.29m、顶板覆土厚4.3m,侧墙高度12.89m,厚0.65m。车站主体标准段宽为19m,为两跨单柱2层车站。围护结构选用1m厚地下连续墙,嵌固深度为4m。车站场区土层的主要物理力学参数见表1。
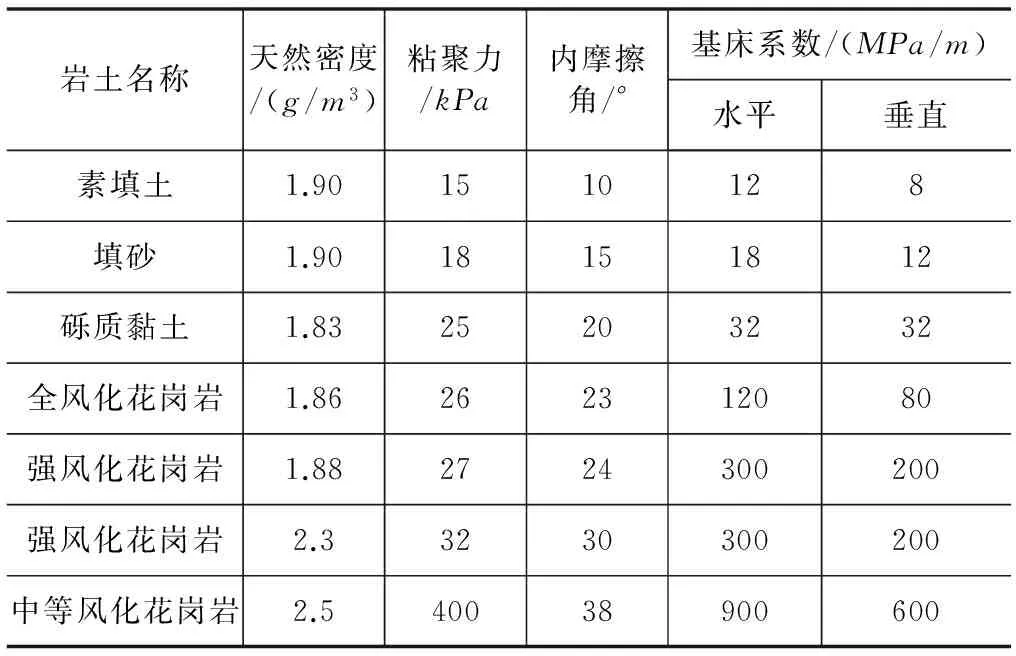
表1 各土层主要设计参数
注:表中只列出了所选取车站横断面内的主要土层信息。
2计算模型及荷载边界条件
原方案着重考虑主体结构与围护结构共同承受荷载时的相互作用,修改方案考虑主体结构单独承受荷载时的内力变化,均选用荷载-结构模型[1]。采用弹簧单元模拟围岩土体,用压杆模拟连续墙与主体结构之间连接,压杆只传递轴力。原方案采用重合墙结构(连续墙与侧墙之间只传递轴力),中板底部采用抗拔桩,记为方案1;修改方案去除地下连续墙,单独分析主体结构受力变形,记为方案2。
计算模型:方案1约束连续墙底部的所有约束以及约束底板中部的竖向位移(模拟抗拔桩);方案2只约束底板中部的竖向位移。两方案的计算模型对比图见图1。
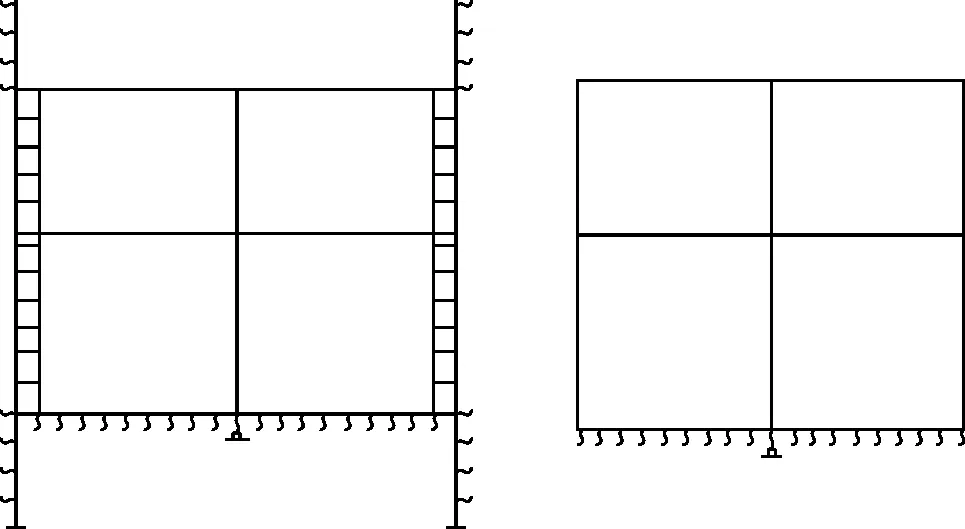
(a)方案1 (b)方案2图1 计算模型对比
3荷载计算
方案1中,按弹性地基上的框架模型考虑连续墙与主体结构的共同作用,荷载采用水土分算,土压力作用在连续墙上、水压力作用在侧墙上[2];方案2去除围护结构,水土荷载均作用于主体结构[3]。两方案均采用极限状态进行荷载组合[4],本文只计算分析承载能力极限状态下的结构内力,并进行后续的比较研究。
4计算结果
4.1SAP84计算结果及分析
方案1采用重合墙结构,采用梁柱单元模拟主体结构与连续墙,连续墙与主体结构之间设置压杆连接,弹性模量取为3×1010Pa,使结构变形更加连续合理。压杆面积取为单元长度乘以每延米,与方案2弯矩计算结果进行比较,见图3。由弯矩对比图比较可知,两方案各部位内力曲线趋势基本一致,可见连续墙对主体结构的内力分布影响并不大。
结构各部位计算关键点见图2,各部位内力相对改变量的大小见图3与图4。各部位内力值见表2与表3(括号内为相对差值百分比,黑体数字表示为该构件的最大内力值)。由表2与表3数据比较可知,两方案主体结构各部位内力值基本一致(除去侧墙中部弯矩与剪力两方案相差较大之外)。各构件最大内力值(黑体)处,基本为方案2较大。另外,表3中,侧墙顶部内力值均为方案1较大。由此可见,方案2中,车站顶板以上侧土压力的缺失(方案1中,这部分侧向压力作用于连续墙),对侧墙顶部内力还是产生了较大影响。
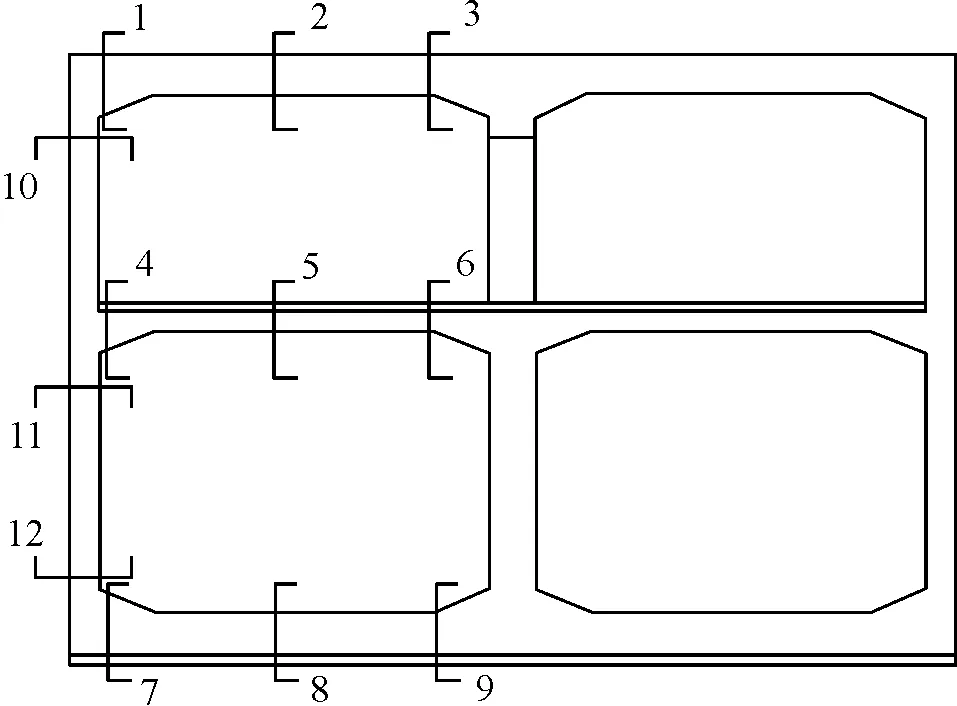
图2 结构计算关键点图
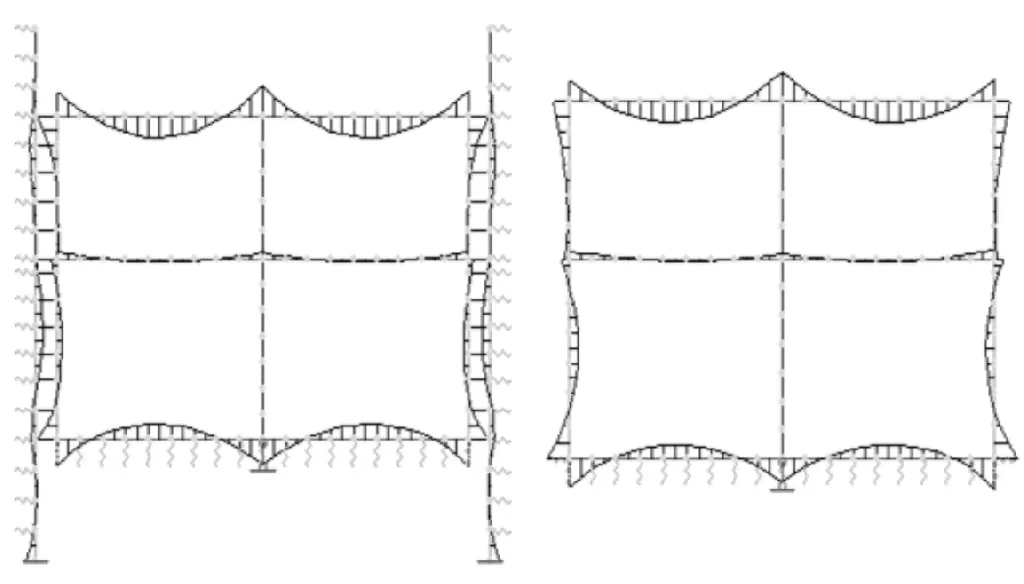
(a)方案1 (b)方案2图3 弯矩对比图(SAP84)

图4 弯矩相对改变量柱状图(SAP84)
表3中,中柱的内力几乎没有变化,这是由于方案2只改变了侧向的荷载,而对竖向荷载没有进行改变,虽然结构在受力中产生的变形会使横向荷载对其在竖向产生影响,但是由计算结果来看,这一影响可忽略不计,即横向荷载的改变不影响主体结构的竖向的受力状态(荷载方向的独立性)。
另外,在表3侧墙截面中,中部位置(图2、图4和图5中关键点11)的内力发生了较大偏差。分析原因:由于方案1中,侧墙与连续墙之间的连接杆件设置为两端铰接只受压形式,而在受力阶段,侧墙中下部位处的部分压杆受拉,既压杆受力为0,导致连续墙上所施加的侧向土压力未能充分传递至主体结构侧墙,使此部分侧墙受力相对偏小;而方案2中,将侧土压力全部作用于侧墙,因此在这个部位上的受力产生了较大变化,而表3中的数据比较也较好的反应出了这一变化。此外,在这一部位,弯矩剪力发生较大变化的同时,而轴力却几乎不变,分析可能原因有两个:一是受压杆只受轴力,消除了弯矩对竖向变形的影响;二是由上文中柱内力变化得出的结论来看,结果也是合理的。
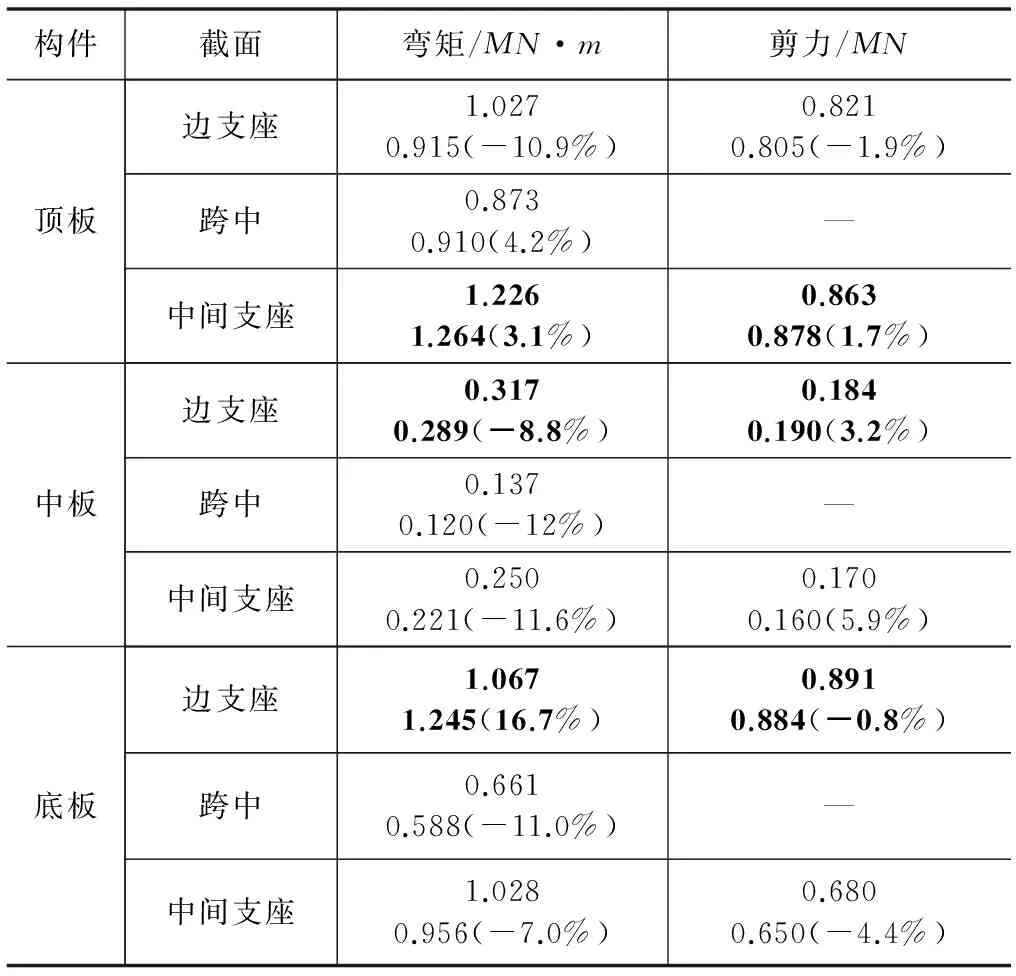
表2 板截面内力对比(SAP84)
注:表中各个单元格,上部为原方案内力值,下部为比较方案内力值,括号内为修改方案角较原方案的相对改变量,下同。
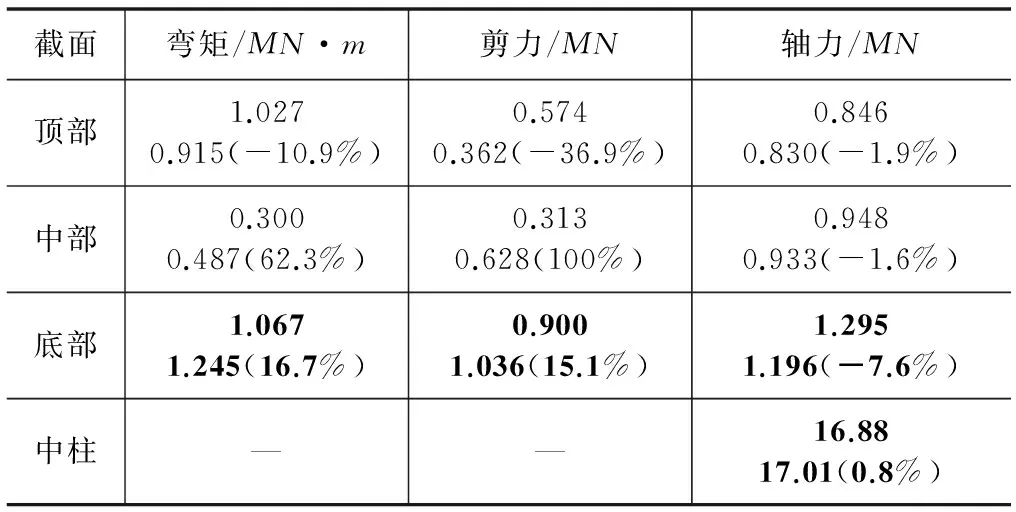
表3 侧墙截面及中柱内力对比(SAP84)

图5 剪力相对改变量柱状图(SAP84)
4.2ANSYS计算结果及分析
方案1中,连续墙与主体结构采用link10杆单元连接,弹性模量取为3×1010Pa,以使连续墙与侧墙的变形更加合理,内力分布更加连续[5]。同样,约束连续墙底端的所有位移,并约束底板中部节点的竖向位移(模拟抗拔桩的作用);方案2则在方案1的基础上,删去连续墙与连接杆,并施加土压力与水压力于主体结构。
弯矩计算结果对比见图6,可见,结构各部位变形曲线基本一致。这也很好的复核了SAP84的计算结果曲线。结构各部位内力相对改变量的大小见图7和图8,结构各部位内力值见表4和表5。对比可知,关键部位内力值基本一致,存在部分部位内力值(侧墙中部,即计算关键点11),方案2远远大于方案1。在结构各构件内力最大值处(黑体字),方案2基本大于方案1。
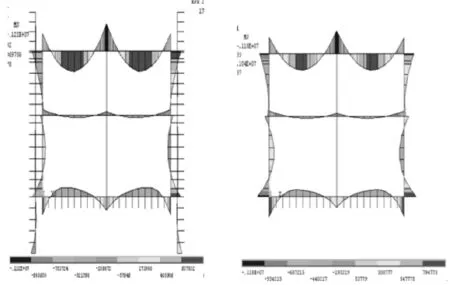
(a)方案1 (b)方案2图6 弯矩对比图(ANSYS)
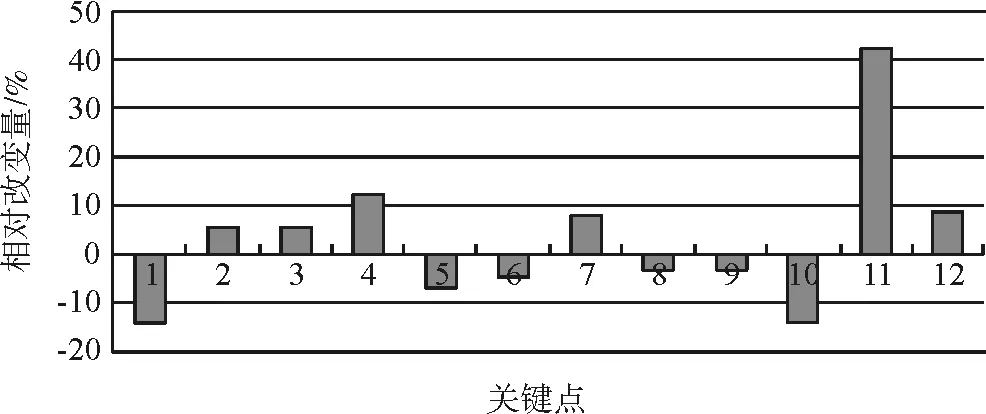
图7 弯矩相对改变量柱状图(ANSYS)
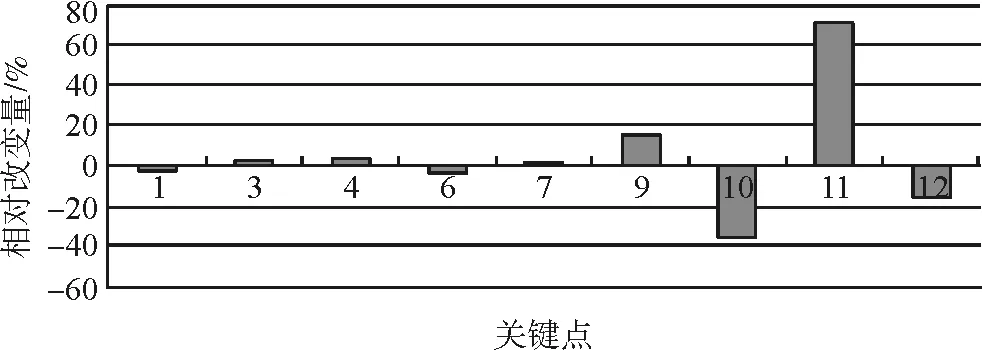
图8 剪力相对改变量柱状图(ANSYS)
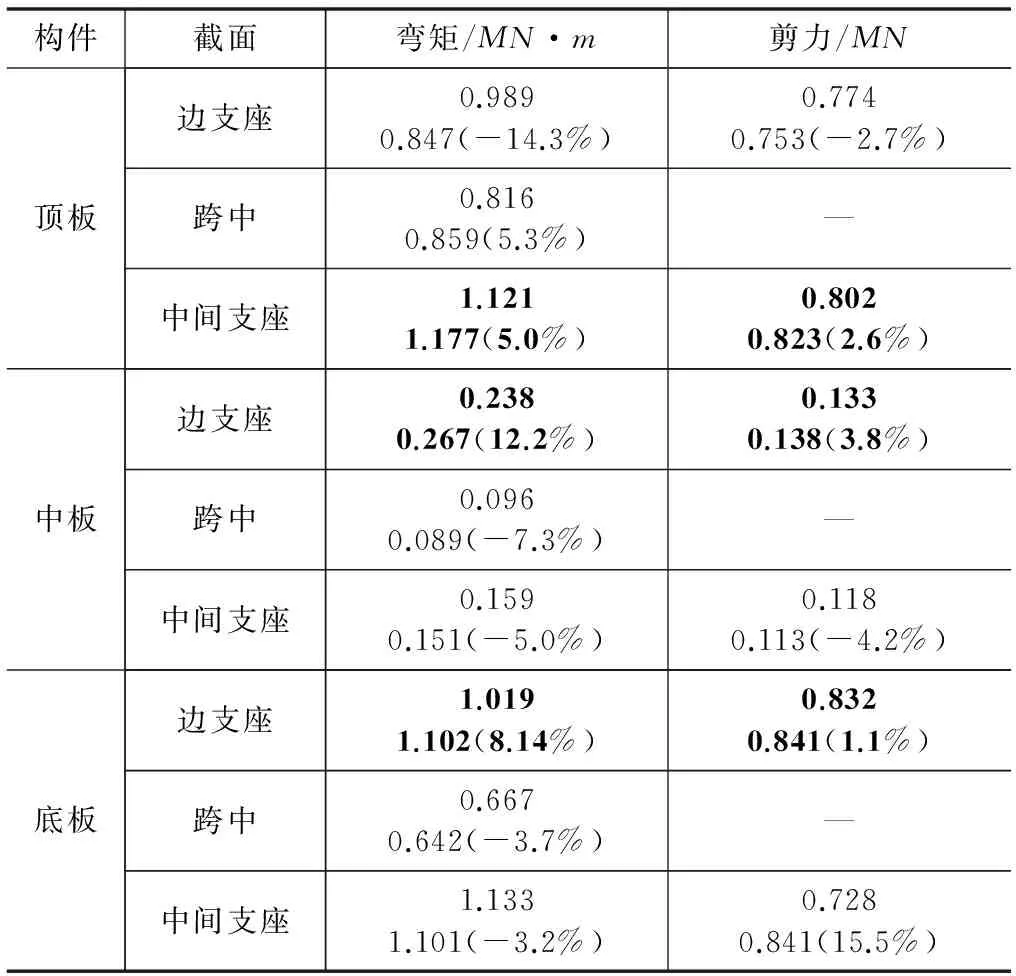
构件截面弯矩/MN·m剪力/MN顶板边支座0.9890.847(-14.3%)0.7740.753(-2.7%)跨中0.8160.859(5.3%)—中间支座1.1211.177(5.0%)0.8020.823(2.6%)中板边支座0.2380.267(12.2%)0.1330.138(3.8%)跨中0.0960.089(-7.3%)—中间支座0.1590.151(-5.0%)0.1180.113(-4.2%)底板边支座1.0191.102(8.14%)0.8320.841(1.1%)跨中0.6670.642(-3.7%)—中间支座1.1331.101(-3.2%)0.7280.841(15.5%)
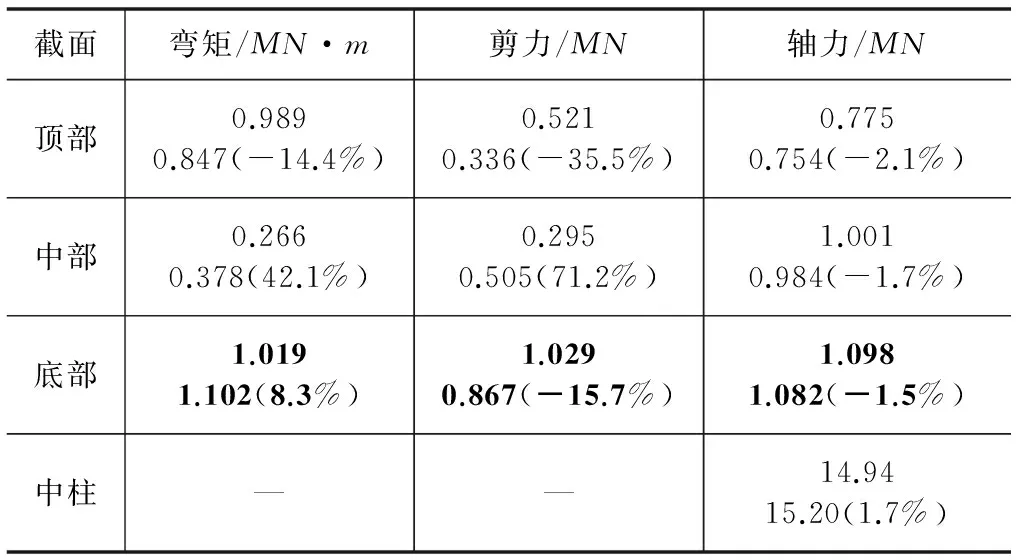
表5 侧墙截面及中柱内力对比(ANSYS)
表5中,侧墙截面中部内力值(关键点11)出现了较大偏差,此情况与SAP84计算结果分析很好的吻合,由此说明:连续墙与侧墙之间的部分压杆在结构受力阶段受力为0(查看单元内力值所得,即压杆为受拉情况),的确对这部分侧墙的受力产生了较大影响。
表5中,各部位的轴力说明了本文4.2章节所得出的结论:横向荷载的改变基本不影响主体结构的竖向受力状态。
5结论
(1)通过两个软件对有无围护结构情况下主体结构的受力结果比较,得知结构内力曲线趋势基本一致。其中:围护结构的有无对侧墙的内力影响十分明显,尤其是侧墙中部,且无围护结构情况下得到的内力值大得多,部分甚至接近2倍大小;而通过侧墙部位以及中柱的轴力值变化可知,围护结构的有无对主体结构竖向轴力的影响却甚微。
(2)通过2个方案的计算结果对比,若以无围护结构情况下得到的内力结果作为基础,对侧墙部位内力值结果乘以一定的系数进行计算,即可得到较为准确的有围护结构情况下的车站内力计算结果,并可以此作为车站主体结构内力计算结果值。由于本次建模计算只为初步分析,具体系数及相关算式有待之后进一步的研究。
(3)当下的车站主体结构内力计算建模基本以文中的方案1为主(即有围护结构),建模流程较为复杂,且存在部分参数的选取疑难点等问题;而不考虑围护结构,直接对主体结构进行内力计算,不但可以大大缩减建模的流程,并且使得到的内力曲线图更加连续合理。因此笔者认为,上述结论二中提到的方案具有很大的研究价值,有望对今后车站建模计算流程的简化提供一定的参考。
参考文献
[1]GB50157-2003 地铁设计规范[S].
[2]GB50009-2012 建筑结构荷载规范[S].
[3]王卫东.地下连续墙作为主体结构的设计[J].建筑结构,2002,32(1): 16-19.
[4]GB50010-2010 混凝土设计规范[S].
[作者简介]李玉琼(1980~),女,工学学士,工程师,主要从事轨道交通投资及轨道交通建设管理工作。
【中图分类号】TU312+.1
【文献标志码】A
[定稿日期]2015-11-10

