矿井风网雅可比矩阵对称特性及并行求解模型

吴奉亮，高佳南，常心坦，李龙清

(1．西安科技大学安全学院，陕西西安　710054;2．西安科技大学教育部西部矿井开采与灾害防治重点实验室，陕西西安　710054)



矿井风网雅可比矩阵对称特性及并行求解模型

吴奉亮1，2，高佳南1，2，常心坦1，2，李龙清1，2

(1．西安科技大学安全学院，陕西西安710054;2．西安科技大学教育部西部矿井开采与灾害防治重点实验室，陕西西安710054)

摘要:为了提高矿井通风网络解算软件的可靠性和求解大型风网时的性能，研究了通风网络雅可比矩阵的对称特性，引入并行计算方法求雅可比矩阵与回路风量修正值。分析了牛顿法求解矿井通风网络的原理，发现并证明了通风网络雅可比矩阵的对称特性，提出用LDLT分解法求解回路风量修正值以有效减少每次迭代的时间。根据多CPU计算机的特点，研究了通风网络雅可比矩阵以及回路风量修正值方程组的并行求解模型。采用VC语言的多线程开发技术实现了通风网络的并行求解，通过两个算例验证了本模型的正确性与高效性。

关键词:矿井通风网络解算;并行计算;牛顿法;雅可比矩阵;对称矩阵

吴奉亮，高佳南，常心坦，等．矿井风网雅可比矩阵对称特性及并行求解模型［J］．煤炭学报，2016，41(6):1454－1459．doi:10．13225/j．cnki．jccs．2015．1302

Wu Fengliang，Gao Jia’nan，Chang Xintan，et al．Symmetry property of Jacobian matrix of mine ventilation network and its parallel calculation model［J］．Journal of China Coal Society，2016，41(6):1454－1459．doi:10．13225/j．cnki．jccs．2015．1302

通风网络解算在矿井通风设计、管理中具有重要作用，因此具备良好性能和人机接口的矿井通风网络解算软件一直倍受学者关注［1－4］。网络解算方法主要有斯拷特－恒斯雷法、牛顿法等。斯拷特－恒斯雷法来源于手工计算矿井通风网络的需要，它在牛顿法的原理上进行了不严密的假设，存在迭代求解回路风量修正值不收敛的可能，为此许多学者对此进行了改进研究［5－10］，有效降低了其不收敛的可能性，但理论上仍存在无解的情况。牛顿法在理论上是严格的［11］，不存在无解的情况，但在求解时必须计算雅可比矩阵的逆阵，对于小型通风网络计算时间较少，当网络规模较大时牛顿法雅可比矩阵及其逆阵的计算量倍增，算法性能明显下降。除了用以模拟风流在井巷中流动的规律外［12－14］，网络解算也被用于模拟采空区流场［15－16］，对于前者风网分支数一般不超过1 000，而对于后者可形成大规模风网，其分支数可超过5 000，其对网络解算的性能提出了更高的要求。

目前基于多CPU计算机的并行计算方兴未艾［17－18］，而矿井通风网络解算理论仍是建立在串行计算流程上的，基于此开发的软件只需要一个CPU的支持，其他CPU都处于闲置。为此本文对矿井通风网络的雅可比矩阵特性及其并行求解技术进行研究，以解决牛顿法在大型通风网络解算方面的不足。

1　通风网络雅可比矩阵的对称特性

1.1牛顿法通风网络解算原理

对于有 n条边、m个节点的矿井风网，设b= n－m+1，其节点风量平衡与回路风压平衡方程见式(1)，(2)。

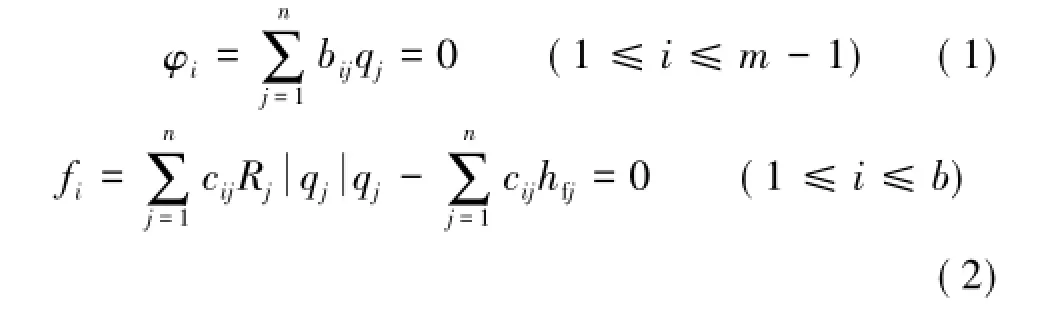
其中，i为整数;cij=1表示分支j与回路i同向，cij=－1表示与回路i反向，cij=0表示分支j不在回路i中; bij=0表示节点i与分支j不相连，bij=1表示分支j风流流入i节点，bij=－1表示j分支风流流出i节点; Rj是分支 j的风阻，N·s2/m8;qj为分支 j的流量，m3/s;hfj为j分支风机风压(是风量的函数)，Pa。根据通风网络理论，风网分支可分为余树支与树支，由结点风量平衡方程(1)可以推得树支风量都可由余树支表示，将风网余树枝风量向量记为Qy=(qy1，qy2，…，qyb)T，则任一分支j的风量qj可表示为

由式(3)可得风网任意分支风量qj对某余树枝l风量qyl的偏导数为

将式(3)代入式(2)得式(5)。采用牛顿法迭代求解式(5)时，记第k次近似解为，…，，将式(5)按泰勒级数展开，并将二次及以上的高阶部分忽略不计，第 k+1次线性化近似式为式(6)。

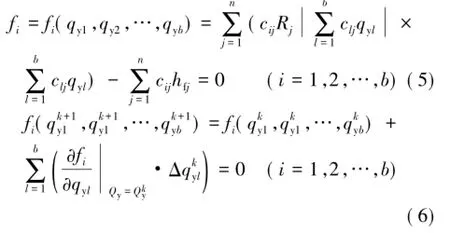
记各回路的风压不平衡值向量F(Qy)=(f1，f2，…，fb)，回路风量修正值向量ΔQy=(Δqy1，Δqy2，…，Δqyb)T，则式(6)可整理为式(7)。

将矩阵∂F/∂Qy记为A，A即为雅可比矩阵。现有基于牛顿法的网络解算都是采用式(8)对A求逆来求。第k+1次的迭代风量，此即为牛顿法解算通风网络的迭代计算模型。当最大元素的绝对值小于给定的计算精度ε时，可被视为风网风量的准确解。

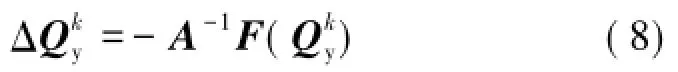
1.2雅可比矩阵的稀疏对称特性

雅可比矩阵展开见式(9)。其矩阵的元素是式(10)在Qy=处取值。由于式(10)中i与l的取值均为(1，2，…，b)，且i和l互换后式(10)保持不变，因此可得式(11)。

式(11)表明雅可比矩阵为对称阵。易知雅可比矩阵元素个数N为b2、非对角线元素的个数为b2－b，则考虑对称特性时需计算的元素个数N1为

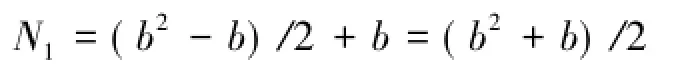
故对称特性下，雅可比矩阵的计算量对原计算量的占比S为

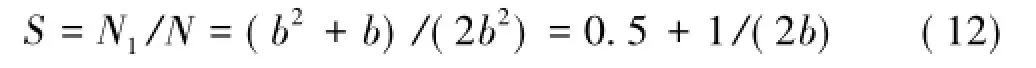
从式(12)可知，当b趋于无穷时，S=50%。如取b=100时，S=50.5%，可见当风网具备一定规模时，雅可比矩阵的对称特性可将其计算量降低约50%。

从式(10)可知，当i回路与l回路无公共分支时，可得式(10)等于0，因为若cij不等于0(j分支在i回路中)，则clj必为0(j分支必定不在l回路中)。根据通风网络独立回路的特性，在大型风网中两回路无公共分支的可能性是较大的，因此大型风网的雅可比矩阵也是稀疏阵。

2　基于LDLT矩阵分解的回路风量修正值求解

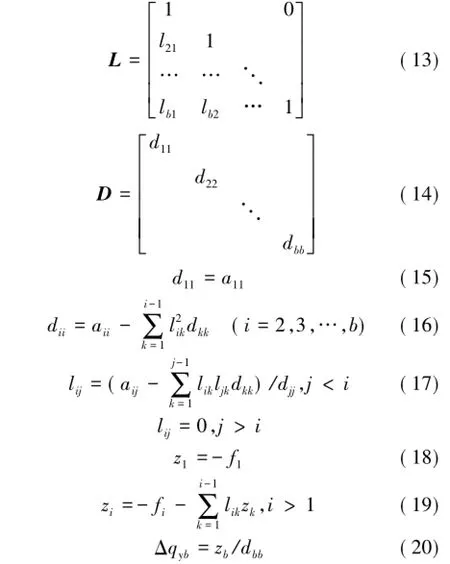
文献［19］表明当线性方程组的系数矩阵为对称阵时，宜用LDLT分解法求解。对式(7)以为未知数的方程组AΔ=－F，使用LDLT分解法时，将对称矩阵A分解为一个下三角矩阵L、一个对角线矩阵 D和一个上三角矩阵 LT的乘积，即A=LDLT，L，D见式(13)，(14)，各元素由式(15)～(17)确定。当L和D确定后，令DLT=z，首先由回代过程求解方程组Lz=－F而得到z，再由方程组DLT=z解出，其计算公式见式(18)～(21)。

3　通风网络解算的并行计算模型

3.1牛顿法矿井通风网络解算流程

根据以上结果可得牛顿法矿井通风网络解算的流程如图1所示，图中划分的各流程之间均是依赖关系，因此并行计算只能存在于各流程内部。从图1可知，雅可比矩阵A的计算与LDLT分解法存在于回路风量修正值的迭代求解循环中(流程6～10)，其计算量占据网络解算的主体，为此网络解算的并行求解模型将基于雅可比矩阵与LDLT分解法的并行计算来建立。

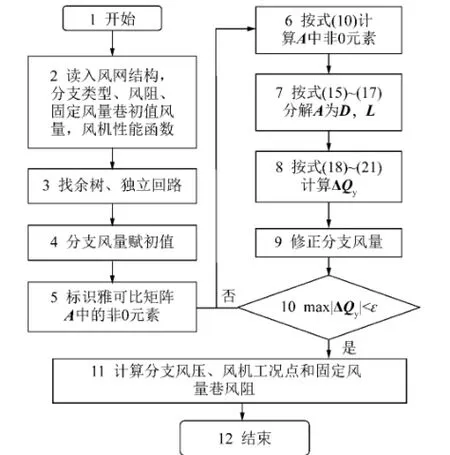
图1　牛顿法矿井通风网络解算流程Fig.1　Flow chart of ventilation network calculation based on Newtown method

3.2网络解算并行计算模型

根据式(10)可知，雅可比矩阵各元素没有相互依赖关系，可以将所有非0元素平均分配到多个线程中并行计算。由于L矩阵对角线元素为常数1，可将D矩阵对角线元素保存于L矩阵中，如图2所示，图中箭头表示由式(15)～(17)中形成的元素依赖关系。由图2可知，D，L矩阵之间以及各矩阵元素内部都存在依赖关系，但L矩阵的同一列元素(图2中用矩形框出)没有依赖关系，可以并行计算。根据以上分析将图1中的第6～8步细化为图3所示流程。图3中第6.1～6.3步完成雅可比矩阵的并行计算:主线程首先获取CPU个数C，并将雅可比矩阵非0

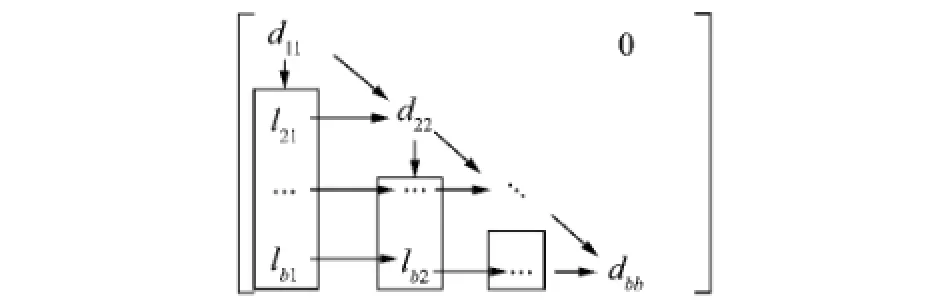
图2　D，L矩阵元素依赖关系Fig.2　Dependence of the elements of the D and L matrixes

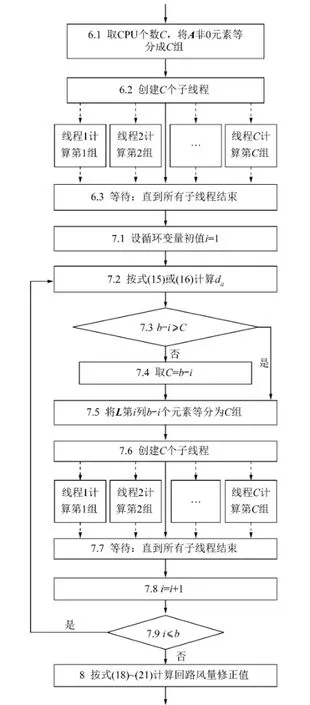
图3　雅可比矩阵与L矩阵的并行求解流程Fig.3　Flow chart of parallel calculation of the Jacobian matrix and L matrix

元素均分成C组(当无法均分时，每组之间的元素个数相差不大于1)，然后创建C个子线程并行计算各组元素，主线程等待各子线程结束后，进入第7步。从7.1～7.9完成L矩阵的并行计算:从L矩阵的第1列(i=1)开始，主线程首先计算D矩阵第i个对角线元素dii，然后判断L矩阵第i列需要计算元素个数b－i是否小于C，如果是则取C=b－i，之后将第i列待求元素分成C组，再创建C个子线程并行计算各组元素，主线程等待各子线程均结束后，再开始计算下一列，如此循环，直到所有列均完成后，进入第8步。综上，A，L矩阵并行计算时子线程之间无信息交互，并发性高，其并行计算是网络解算并行计算模型的核心。

4　算例分析

在已有的网络解算软件基础之上，采用VC++实现了以上模型，现通过一简单风网与一大型风网分别对模型的正确性与性能进行验证。

4.1简单风网算例

图4风网具有12条边，7个节点，分支风阻均取0.1 N·s2/m8，编号12是风机分支，风机性能函数hf=3 204.2－4.91q12+0.025q122－0.000 2q123，有效风量范围为［50，220］。分支7～12是6条余树枝，故Qy=(qy1，qy2，…，qy6)T=(q7，q8，q9，q10，q11，q12)T，各回路编号及所含分支分别为1(7，－6，－5，－4，2，3)，2(8，－5，－4，2)，3(9，－3，－2，4)，4(10，－4，2)，5 (11，－3，－2，4，5)，6(12，1，4，5，6)，分支号为负表示其方向与余树支方向相反。分支12的风量初值取135 m3/s，其他余树支风量初值取1 m3/s，则分支1～12风量初值依次为(135.0，－1.0，1.0，134.0，134.0，134.0，1.0，1.0，1.0，1.0，1.0，135.0)。以第1次迭代计算雅可比矩阵a23，a32元素为例，按式(3)写出2，3回路中树支风量的计算式分别为:q5=－q8－q7+q11+q12，q4=－q8－q7+q9－q10+q11+q12，q3=q7－q9－q11，q2=q7+q8－ q9+q10－q11;回路风压代数和函数分别为:f2=R8－。易知均为0，故

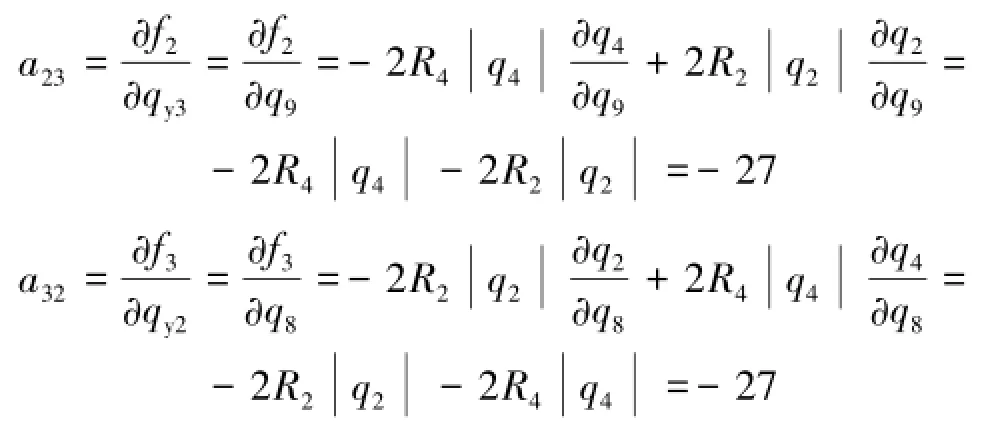
可见此对称位置两元素相等，经验证所有对称位置的元素均相等。采用运行于4核CPU中的程序计算，需计算雅可比矩阵元素总数为21，软件创建的第1个线程计算6个元素，其他3个线程各计算5个元素，得到整个雅可比矩阵见式(22)，对应图2中的D，L矩阵元素见式(23)。

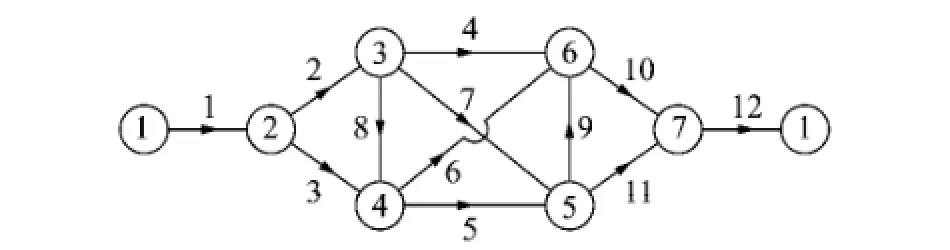
图4 简单风网Fig.4　A simple ventilation network sample

经过7次迭代后求得各分支风量向量为(129.4，64.7，64.7，32.3，32.3，32.3，32.3，0，0，64.7，64.7，129.4)。

4.2大型风网实例

引用文献［15］中使用网络解算求采空区流场的实例，如图5所示，采煤工作面长度为120 m，采空区冒落带走向长度为200 m，采空区被划分为许多纵横交错的滤流分支，滤流分支特有的阻力特性方程［15－16］将采空区多孔介质转换成了网络系统，可用网络解算方法计算其流场。根据其原理，滤流分支长度越小模拟精度越高。图5是将滤流横向长度取为2 m、纵向取为4 m形成的风网，其分支数达到6 135，节点数为 3 133，独立回路数 3 003。采用 4核CPU(频率2.5 GHz)、在Windows 7操作系统下解算以上风网，得到以下结果:

图5　网络化采空区后的大型风网Fig.5　A big ventilation network in a gob area divided by branches

(1)雅可比矩阵共有9 012 004个元素，其中非0元素880 402个，仅占总数的9.8%。

(2)考虑雅可比矩阵对称性，但不考虑稀疏性时，单线程计算时间是4 min，多线程并行计算时间减至94 s。考虑对称性与稀疏性(只计算非0元素)、采用并行计算，雅可比矩阵的计算时间减至8 s。

(3)单线程LDLT分解法求一次回路风量修正值计算时间为13 min，基于多线程并行计算时间为4 min。

图6是程序运行时4个CPU的使用率。每个CPU的曲线均分为3段:第1段是软件单线程运行图1中第1～5步，CPU的平均使用率不到30%;第2段是计算雅可比矩阵，时间为8 s左右，CPU使用率均为100%;第3段是运行图3中7.2～7.9步，曲线的振荡是循环中不断的创建线程与退出线程形成的，但CPU的平均使用率均超过90%。整个解算过程迭代了25次收敛，共耗时约110 min。

图6　基于并行计算的网络解算CPU使用率Fig.6　The usage rate of 4 CPUs when parallel calculating a ventilation network

按25次迭代、每次迭代耗时38 min计算，普通牛顿法将耗时15.8 h。可见本文研究对于大型风网的解算具有明显优势。

5　结　　论

(1)矿井通风网络雅可比矩阵是稀疏对称阵，采用LDLT矩阵分解求回路风量修正值具有更高的性能。通过分析基于牛顿法的矿井通风网络解算原理，发现了雅可比矩阵的对称特性。用LDLT矩阵分解法求以对称雅可比矩阵为系数矩阵的回路风量修正值方程组，提高了牛顿法解算矿井通风网络的性能。通过一简单算例对雅可比矩阵的对称性及LDLT分解法应用于网络解算的正确性进行了验证。

(2)矿井通风网络解算的回路风量修正值求解具有显著的并行特征。网络解算主要耗时于回路风量修正值的迭代计算，每一次迭代包括求雅可比矩阵与解以回路风量修正值为未知数的线性方程组。雅可比矩阵、L矩阵并行计算过程中，子线程之间无信息交互，并发性高。通过实现雅可比矩阵与L矩阵的并行计算，构建了矿井通风网络解算的并行求解模型。

(3)与普通网络解算软件相比，基于牛顿法并行计算的网络解算在当前多CPU个人计算机上性能大幅提升。通过对一含有6 135条分支的风网进行验证，软件可以在2 h左右给出常规网络解算难以求解的结果。

参考文献:

［1］王德明，周福宝．基于WINDOWS的矿井通风网络解算软件的研制［J］．中国矿业大学学报，2000，29(1):41－44．Wang Deming，Zhou Fubao．Study on Windows-Based software for mine ventilation network solution［J］．Journal of China University of Mining＆Technology，2009，29(1):41－44．

［2］刘剑．流体网络理论［M］．北京:煤炭工业出版社，2002．

［3］王德明，王俊，周福宝．基于面向对象技术开发的矿井通风图形系统［J］．煤炭学报，2000，25(5):510－513．Wang Deming，Wang Jun，Zhou Fubao．Developed mine ventilation graphics system based on the object-oriented technologies［J］．Journal of China Coal Society，2000，25(5):510－513．

［4］吴奉亮，周澎，李晖，等．基于智能对象的通风CAD模型研究［J］．煤炭科学技术，2009，37(5):54－57．Wu Fengliang，Zhou Peng，Li Hui，et al．Research on the model of mine ventilation CAD based on the intelligent object［J］．Coal Science and Technology，2009，37(5):54－57．

［5］周心权，吴兵．定向圈划回路法探讨［J］．煤矿安全，1993(4): 10－12．Zhou Xinquan，Wu Bing．The exploration of directional circle loop method［J］．Safety in Coal Mines，1993(4):10－12．

［6］魏连江，周福宝，朱华新．通风网络拓扑理论及通路算法研究［J］．煤炭学报，2008，33(8):926－930．Wei Lianjiang，Zhou Fubao，Zhu Huaxin．Topology theory of ventilation network and path algorithm［J］．Journal of China Coal Society，2008，33(8):926－930．

［7］孙臣良，题正义，赵铁文．基于改进Cross算法的矿井复杂风网可视化解算系统［J］．辽宁工程技术大学学报(自然科学版)， 2008，28(S1):25－27．Sun Chenliang，Ti Zhengyi，Zhao Tiewen．Visual calculation system of complicated ventilation network of coal mine based on improvedcrossalgorithm［J］．JournalofLiaoningTechnical University(Natural Science)，2008，28(S1):25－27．

［8］钟德云，王李管，毕林，等．基于回路风量法的复杂矿井通风网络解算算法［J］．煤炭学报，2015，40(2):365－370．Zhong Deyun，Wang Liguan，Bi Lin，et al．Algorithm of complex ventilation network solution based on circuit air quantity method［J］．Journal of China Coal Society，2015，40(2):365－370．

［9］马心校．解算矿井通风网络不收敛的一种处理方法［J］．煤炭工程师，1990(3):8－17．Ma Xinxiao．Method of solving the problem of not convergence in mineventilationnetworkcalculation［J］．CoalEngineer，1990(3):8－17．

［10］杨鑫祥，肖伟，武猛猛，等．矿井通风网络解算软件的改进研究与实现［J］．矿业研究与开发，2015，35(4):80－83．Yang Xinxiang，Xiao Wei，Wu Mengmeng，et al．Improvement and realization of the software for mine improvement and realization of the software for mine ventilation network solution［J］．Mining R．＆D．，2015，35(4):80－83．

［11］李恕和，王义章．矿井通风网络计算的牛顿法［J］．煤炭学报，1982，7(4):52－62．Li Shuhe，Wang Yizhang．The newtow method for calculating the mine ventilation networks［J］．Journal of China Coal Society，1982，7(4):52－62．

［12］张国枢．通风安全学［M］．徐州:中国矿业大学出版社，2000．

［13］吴奉亮．对角式通风系统封闭型网络降阻分析［J］．煤矿安全，2011，42(7):135－138．Wu Fengliang．Pressure reduction analysis of closed network in a diagonal ventilation system［J］．Safety in Coal Mines，2011，42(7):135－138．

［14］El-Nagdy K A，Shoaib A M．Alternate solutions for mine ventilation network to keep a preassigned fixed quantity in a working place［J］．International Journal of Coal Science＆ Technology，2015，2(4):269－278．

［15］刘泽功．通风安全工程计算机模拟与预测［M］．北京:煤炭工业出版社，1995:172－180．

［16］魏引尚，邵炜航，王慧．基于网络解算的采空区漏风分布计算模式［J］．煤矿安全，2011，42(1):46－49．Wei Yingshang，Shao Weihang，Wang Hui．Calculation model of gob air leakage based on the ventilation network calculation ［J］．Safety in Coal Mines，2011，42(1):46－49．

［17］陈国良．并行算法的设计与分析［M］．北京:高等教育出版社，2009．

［18］谷照升．基于多核CPU的并行计算设计［J］．长春工程学院学报(自然科学版)，2009，10(3):92－94．Gu Zhaosheng．Design for Multi-kernel CPU based parallel computing［J］．Journal of Changchun Institute of Technology(Natural Sciences Edition)，2009，10(3):92－94．

［19］徐士良．C常用算法程序集(第二版)［M］．北京:清华大学出版社，2004．

中图分类号:TD722

文献标志码:A

文章编号:0253－9993(2016)06－1454－06

收稿日期:2015－09－10修回日期:2015－12－08责任编辑:毕永华

基金项目:国家自然科学基金青年基金资助项目(51204135，51104116)

作者简介:吴奉亮(1977—)，男，四川新都人，副教授，硕士生导师。E－mail:15038537@qq．com

Symmetry property of Jacobian matrix of mine ventilation network and its parallel calculation model

WU Feng-liang1，2，GAO Jia-nan1，2，CHANG Xin-tan1，2，LI Long-qing1，2
(1．School of Safety Engineering，Xi’an University of Science and Technology，Xi’an710054，China;2．Key Laboratory of Western Mine＆Hazard Prevention，China Ministry of Education，Xi’an University of Science and Technology，Xi’an710054，China)

Abstract:A parallel calculation and symmetry property of the Jacobian matrix deduced from a ventilation network is adopted in this study to enhance the reliability and the performance of software on calculating Coalmine’s ventilation network．The theory of solving Coalmine’s ventilation network by using Newtown method is presented in some details，and then the symmetry characteristic of the Jacobian matrix of a ventilation network is illustrated．A LDLTdecomposition method is put forward to solve the corrected value of flow rate in a circuit，which can save a lot of time during each iteration．To take the most advantages of a multi-CPU computer，a parallel model is employed to solve the Jacobian matrix and the equations of corrected values in circuits of a ventilation network．This parallel model is achieved using the technology of multi-threads in VC language，whose validity and performance are verified by running it in two ventilation network samples．

Key words:mine ventilation network calculation;parallel calculation;Newtown method;Jacobian matrix;symmetric matrix