基于PCA-SIFT特征与贝叶斯决策的图像分类算法
涂秋洁 王 晅
(陕西师范大学物理学与信息技术学院 陕西 西安 710119)
基于PCA-SIFT特征与贝叶斯决策的图像分类算法
涂秋洁王晅
(陕西师范大学物理学与信息技术学院陕西 西安 710119)
摘要针对现有的基于SIFT特征的图像分类算法具有较大的储存空间需求及对图像背景较为敏感的问题,提出一种基于PCA-SIFT特征和贝叶斯决策的图像分类算法。该算法首先应用主成分分析将SIFT特征从128维降为36维,在训练过程中,对训练样本图像的PCA-SIFT进行区域匹配。基于匹配率选择目标图像中的稳定PCA-SIFT以提高算法对背景图像干扰的鲁棒性,然后应用最大似然估计估计概率分布参数,最后,应用贝叶斯决策理论实现图像分类。仿真实验表明,该算法与现有的SIFT图像分类算法相比分类精度高,而且具有最小的储存空间需求与较高的计算效率。
关键词PCASIFT聚类贝叶斯决策图像分类
0引言
对几何变换如平移、旋转与尺度变换的不变图像目标描述对图像分析、目标识别与分类等具有非常重要的意义[1],现有的不变特征描述主要分为全局、局部与基于目标轮廓的特征表示三类[2]。全局特征只适合于刚性对象的识别与分类,而且对图像剪切、遮挡、光照改变与视角改变较为敏感。基于目标轮廓的特征,如张量尺度、曲率尺度、内距[3]与多尺度距[4]等仅具有部分几何变换不变性,而且对图像剪切、遮挡、光照改变与视角改变较为敏感,另外,其性能严重依赖于边缘检测与图像分割的结果。
基于图像局部特征的不变描述方法,如GLOH[5],Harris-Affine[6],SIFT[7],SURF[8]等对图像的剪切、遮挡、尺度、位置、方向、光照及轻微的视角改变具有很好的稳定性,而且突破了刚性对象的限制。在这些方法中,SIFT已被证实具有最好的描述性能[9],被广泛应用在图像区域匹配、目标检测与图像检索中。但是,由于图像局部特征的固有特性,不太适合图像识别与分类问题。首先,对于一幅图像,通常会检测到成百上千个关键点,每个关键点需要128维的向量表示,这需要较大的储存空间保存图像的类别模式特征。其次,两幅图像的特征点匹配的计算复杂度为128×N2,N为单幅图像的关键点数量,这使得基于局部特征的图像分类很难满足实际应用的计算效率要求。最后,由于图像区域匹配与分类的目标与要求不同,所以分类精度也达不到实际应用的要求。
最近,出现了许多研究工作将SIFT从图像区域匹配推广到图像分类问题中,较早的SIFT图像分类算法是基于图像区域匹配的算法[10,11],这些算法首先将待识别图像与已知类别的训练样本图像进行区域匹配,然后基于区域匹配数量实现模式分类。该类算法具有较高的储存空间要求与计算复杂度,另外,只考虑区域匹配数量很难获得高的分类精度。随后出现了基于编码或聚类的SIFT图像分类算法[12-16],该类算法的主要创意来源于文本数据挖掘的BoW(bag-of-words)概念,将图像所提取的关键点特征当作视觉词汇,然后,基于图像中出现的视觉词汇的频次或编码结果作为特征实现分类[12-14]. 但是,BOW模型直接应用于SIFT特征没有考虑局部特征点的空间位置,所以基于此产生的频次或编码特征缺失了图像的空间组织信息。针对此问题,Lazebnik等提出了SPM算法[15], 该算法将图像在不同尺度上划分为多个细段,计算每个细段内的BOW的直方图,然后,链接所有直方图形成图像的最终表示。SPM算法虽然部分考虑了图像的空间组织信息,获得了较好的分类精度,但其特征具有很高的维数,这严重制约了分类过程的计算效率,特别是使用非线性分类器时,其计算复杂度呈指数增长。为了降低SPM的计算复杂度,文献[16]在SPM的基础上应用非线性编码技术将特征转化为近似线性可分问题,然后应用线性分类器实现分类,获得了较好的分类效果。最新的此方面的研究[17-19]主要集中在将稀疏编码或机器学习应用到BOW或SPM模型中,从而降低图像的特征向量维数或提升其表示能力,以提升分类过程的计算效率与分类精度。如Yang等[17]应用稀疏编码代替SPM中的向量量化,提出了稀疏SPM(ScSPM)算法,Wang[18]将稀疏编码过程转化为局部约束下的优化问题,提出了LLC算法。Zhang等[19]将低阶分解与拉普拉斯群稀疏编码应用于BOF模型中,实现了图像分类等。
现有的基于SIFT的图像分类算法虽然对图像的剪切、遮挡、尺度、位置、方向、光照及轻微的视角改变具有很好的稳定性,但是,其储存需求与计算效率并不能满足实际应用的要求,另外,SIFT描述字已经被证实在图像区域匹配和目标检测中具有非常好的性能,基于编码的方法并没有充分利用SIFT的这一优良特性,所以其分类精度也达不到令人满意的效果。针对此问题,本文提出了一种基于SIFT区域匹配与贝叶斯决策的图像分类算法,为了有效地降低算法的特征维数,使用主成分分析(PCA)将SIFT特征从128维降为36维。在训练过程中,将属于同类的样本图像的PCA-SIFT进行互配,根据匹配率选择该类图像较为稳定的PCA-SIFT特征应用最大似然估计估计其均值向量与协方差矩阵,然后基于贝叶斯决策理论进行分类。仿真实验表明,该算法具有较高的分类精度,而且由于其在分类过程中只涉及简单的数值计算,具有较高的计算效率。
1SIFT算法与PCA-SIFT简介
1.1SIFT算法
经典SIFT算法[7]分为多尺度空间极值点检测、关键点筛选、关键点方向校正与描述字生成四个子过程。在多尺度空间极值点检测过程中,首先将待检测图像I(x,y)与相邻尺度的高斯差分函数进行卷积形成多尺度空间表示,即:
G(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)
(1)
其中,* 表示沿x与y方向的卷积,高斯函数G(x,y,σ)定义为:
L(x,y,σ)=G(x,y,σ)*I(x,y)
(2)
然后,检测多尺度空间中的极值点作为候选关键点,检测规则为该点是某一尺度空间相邻8个像素及其上、下相邻尺度空间中同位置的18个像素的极值点。在这些候选关键点中,会存在对局部噪声干扰较为敏感的不稳定的关键点。针对这一问题,SIFT算法引入Hessian矩阵对候选关键点进行进一步筛选,候选关键点的Hessian矩阵定义为:
(3)
其中:
(4)
(5)
(6)
其中,D(x,y,σ)为该关键点所在的尺度空间,不稳定的关键点的主方向响应会远远大于其垂直方向,如果α表示Hessian矩阵主方向所对应的特征值,β为其垂直方向所对应的特征值,则有:
α+β=Tr(H)=Dxx+Dyy
(7)
(8)
改写可得:
(9)
其中,γ=α/β,因此,候选关键点的筛选规则为:
(10)
其中,T为筛选阈值。通过上述两个过程,在图像I(x,y)的多尺度空间可以检测若干稳定的关键点,为了获得旋转不变性,还要对关键点进行方向校正,其基本原理是在确定该关键点的SIFT描述字时,将坐标轴旋转到该关键点的主方向。关键点的主方向通过计算该关键点邻域梯度分布直方图的峰值,然后再进行二次函数的拟合来确定。在统计邻域梯度分布直方图时,对梯度幅值进行方差为尺度因子σ1.5倍的高斯函数进行加权。
在关键点描述字生成过程中,首先以关键点为中心,旋转其邻域使得坐标轴x与该关键点的主方向重合,并且根据其尺度因子σ进行相应的尺度变换,然后计算其16×16邻域像素点的梯度幅值与方向,将16×16邻域划分为16个4×4的子块,计算每个子块8方向的梯度直方图,将16个子块的梯度直方图的值按从左到右,从上到下的次序排列起来(见图1所示),然后进行归一化,形成该关键点128维的SIFT描述字。

图1 SIFT描述字计算过程图示
1.2PCA-SIFT 算法
直接利用SIFT算法提取的特征进行后续的图像处理,无论是从算法的计算复杂度,还是从算法的性能来看,都是不可取的。所以需要对128维SIFT特征进行降维。利用主成分分析的方法对SIFT算法进行改进,具体实现过程如下。
确定样本图像I(x,y)的关键点 ( 假设为n个),针对每个关键点提取SIFT特征,共128维,将其组成特征矩阵X=(x1,x2,…,xn),维数为n×128。
计算特征向量的均值:
(11)
计算特征向量的协方差矩阵:
(12)
求取协方差矩阵的特征值和特征向量。由于Cx是实对称的,故可以找到128个正交的特征向量,设特征值λi对应的特征向量为ei,将特征值从大到小排列。
将最大的k个特征值对应的特征向量ek组成变换矩阵A,A的维数为128×k,k的取值大小决定最终特征向量的维数。
Ke等的工作[22]表明,当k选择36时,PCA-SIFT具有最佳的区域匹配和表示能力,而且在他们的实验中,PCA-SIFT区域匹配和表示能力好于原SIFT特征。本文选择k=36,变换矩阵A生成过程采用与文献[22]相似的方法,即选择一组与识别问题无关而且差异较大的图像,抽取20 000多个SIFT特征根据上述方法进行PCA降维,获得128×36维的变换矩A,将此变换矩阵保存起来,应用下式进行降维:
y=Ax
(13)
其中,x为原SIFT特征,y为对应的36维的PCA-SIFT。
2本文算法
本文算法的实现过程如图2所示。
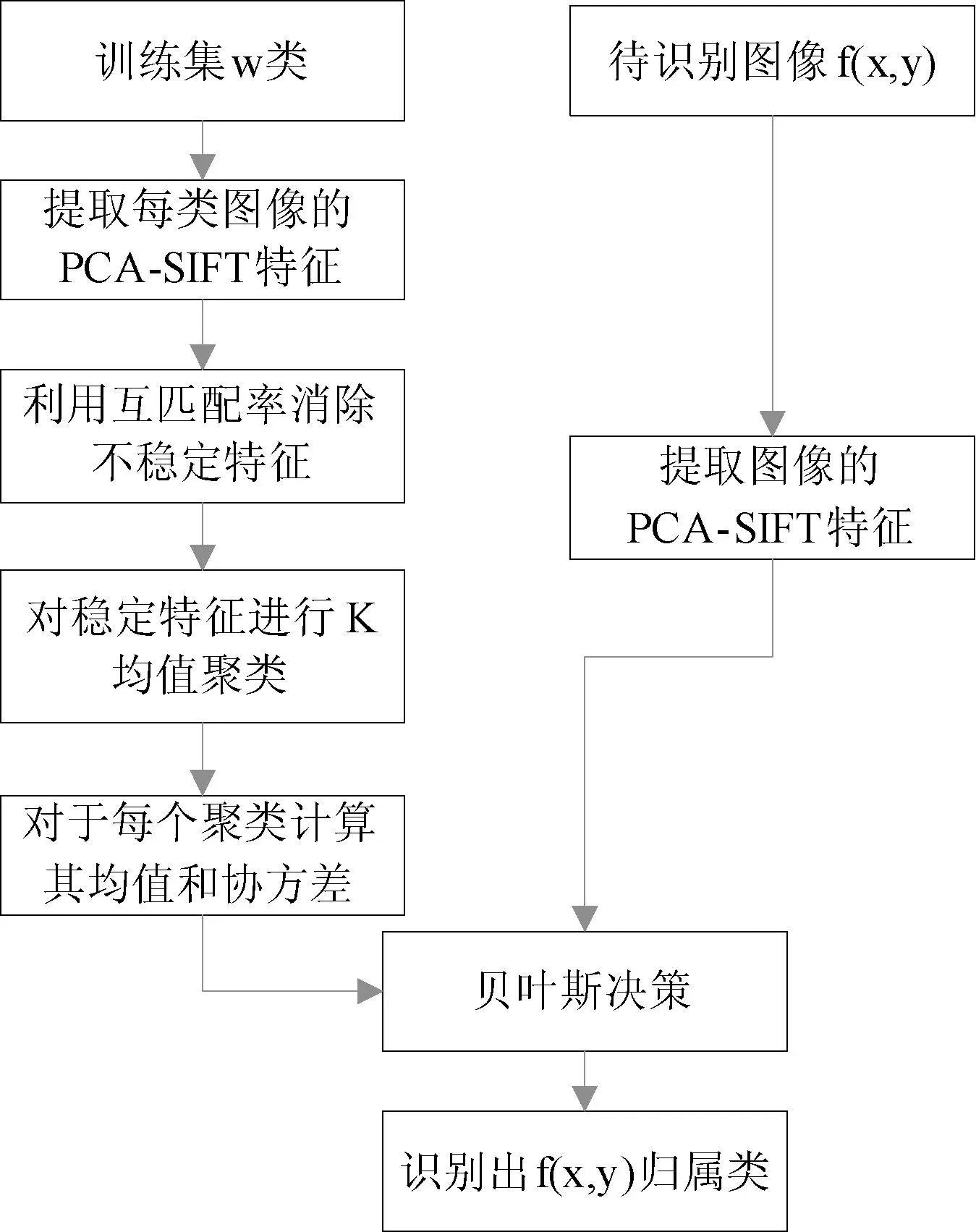
图2 基于PCA-SIFT与贝叶斯决策的图像分类算法实现流程图
2.1训练过程
本文算法首先应用式(10)对所提取到的SIFT特征进行降维。在训练过程中,对同类训练样本图像所提取到的PCA-SIFT特征进行互配,计算每个PCA-SIFT的互配率,具体作法如下,首先在同一类别的训练样本图像中随机选择一幅训练样本图像fw(x,y),将其与同类的其它训练样本图像基于PCA-SIFT进行区域匹配,对于图像fw(x,y)中的某一PCA-SIFT特征ywi,其互配率s(ywi)定义为:
(14)
其中,Nw为训练集中w类样本图像总数,nwi为与特征ywi区域匹配成功的该类训练样本图像总数。互配率s(ywi)反映了特征ywi在该类图像中的稳定程度,如果s(ywi)趋近于1,说明对应特征ywi在该类图像中为目标图像的稳定关键点,在分类过程中应重点考虑,如果s(ywi)趋近于0,则特征ywi为该类图像中背景图像或其它干扰所形成的关键点,在分类过程中可能会干扰分类结果。基于此,我们根据互配率s(ywi)的大小对特征ywi进行进一步筛选,如果s(ywi)>T,则特征ywi在该类图像中为目标图像的稳定关键点保留,否则,即舍去。其中T为阈值,根据具体分类问题基于实验确定。
对于同一目标图像的稳定关键点特征ywi,在不同的训练样本图像和测试图像中,其值由于噪声或成像设备等因素会发生一定漂移,假定其变化符合多维正太分布,有:
(15)
其中,μwi与∑wi为关键点特征ywi概率公布的均值向量与协方差矩阵,可以在训练过程中基于最大似然估计进行估算[23],有:
(16)
(17)
其中,ywij为特征ywi在同类的第j幅训练样本图像对应的区域匹配特征。由于PCA降维使得特征ywi的各分量不相关,基于正太分布假设,理论上∑wi应为对角矩阵,在实验中,我们发现,∑wi虽然不是对角矩阵,但其非对角原素值远小于对角原素,我们只保留∑wi矩阵的对角原素,其它原素为零作为协方差矩阵的近似估计。将w类所有稳定特征对应的μwi、∑wi与互配率s(ywi)作为该类别的模式特征。
2.2基于贝叶斯决策的图像分类
给定未知样本图像f(x,y),提取其所有SIFT特征,应用式(10)获得其对应的PCA-SIFT特征yl,1≤l≤N。考虑到这些特征中一部分特征属于背景图像,与分类的目标图像无关,在分类过程中应舍去,则,样本图像f(x,y)的类概率:
(18)
(19)
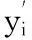
(20)
其中,Nw为w类的图像稳定的PCI-SIFT特征总数,根据贝叶斯公式,给定未知样本f(x,y),其属于类别w的后验概率为:
(21)
则未知样本f(x,y)应分类到后验概率p(w/f(x,y))最大的对应类别中,由于概率函数的非负性,上述分类规则等价于求p(f(x,y)/w)p(w)的最大值。假定在分类过程中,各个训练类别的先验概率类p(w)相同,则上述规则等价于计算p(f(x,y)/w)的最大值,将式(20)代入式(18),有:
(22)
为了简化计算,对式(22)两边取对数,有:
(23)
去掉上式中不影响比较结果的常数项因子,则取上式的最大值等价于计算下式的最小值:
(24)
则,分类规则为:
(25)
考虑到在训练过程中,互配率s(ywi)较大的特征在该类图像中为目标图像的稳定关键点,在分类过程中应重点考,因此,式(25)的分类规则最后修正为:
(26)
2.3方法储存需求与计算效率分析

表1 储存需求与计算效率比较
3实验结果与分析
实验采用文献中常用的两个标准数据库Caltech-101[24]、15-Scene[15]进行了仿真测试,并与基于SIFT最新的、有代表性的图像分类方法如SPM[15]、ScSPM[17]、LLC[18]、拉普拉斯群稀疏编码[19]、自适应分块机器学习[20]与空域金字塔稀疏编码方法[21]进行了性能比较。
实验115-Scene数据库包含了15类图像,包括床、郊区、工业园区、厨房、卧室、海岸、森林、高速路等一共4485幅图像。对每一类选取30幅图像作为训练图像,其它图像作为测试图像。实验结果见表2所示。如表2所示,各种改进的SPM算法较原SPM算法分类精度有不同程度的提高,基于机器学习的改进方法分类精度高于基于稀疏编码的改进算法,我们的方法较现有的方法具有最好的分类精度。
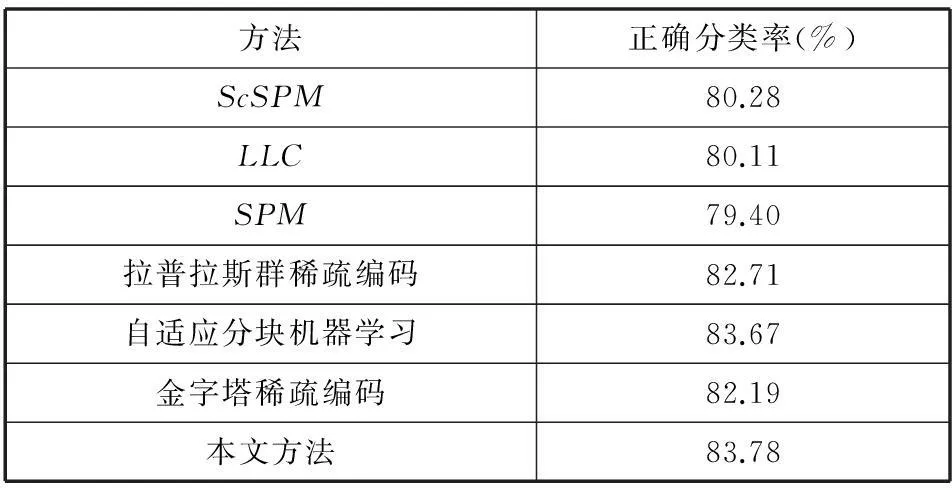
表2 对15-Scene标准数据库的分类精度
实验2Caltech-101 数据库包含了101类共9144幅图像(包含有动物,花,人脸等)。每一类图像有31~800幅方向、光照、大小不同的样本图像。对每一类图像选取30幅图像作为训练样本,其他图像作为测试样本。应用我们的方法与上述方法进行分类,结果见表3所示。由表3可以看出,上述方法该数据库的分类精度较实验1都有不同程度的下降,主要原因是Caltech-101 数据库的样本图像方向、光照、大小明显不同,尤其是其分类的目标图像都具有不同的背景,而我们的方法通过训练过程中的互配率对图像的特征点进行了筛选,在分类过程中,互配率大的特征点对分类结果贡献在。这在一定程度上降低了图像背景中的特征点对分类过程的干扰,所以我们方法较现有方法具有最好的分类精度,而且在两个数据库上的分类精度下降最小。
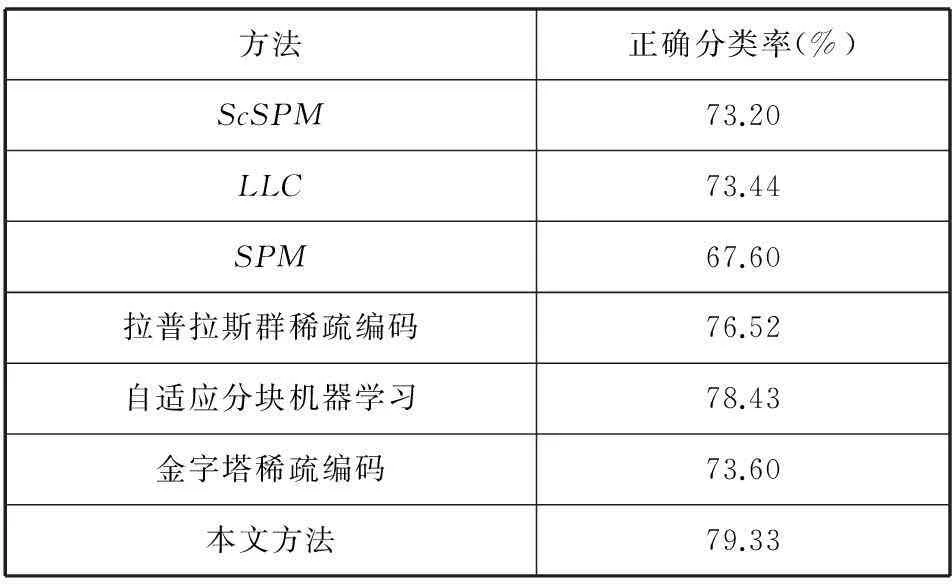
表3 对Caltech-101 标准数据库的分类精度
4结语
本文提出了基于PCASIFT特征和贝叶斯决策的图像分类方法,PCASIFT特征不仅有效地继承了SIFT特征在平移、旋转、尺度变换和光照改变下的鲁棒性,而且解决了SIFT特征维度较高的问题,大大降低了计算的复杂度。实验结果表明,本文的方法比现有算法分类精度高,而且对背景图像的干扰具有较高的鲁棒性。
参考文献
[1]WangX,XiaoB,MaJF,etal.ScalingandrotationinvariantanalysisapproachtoobjectrecognitionbasedonRadonandFourier-Mellintransforms[J].PatternRecognition,2007(40):3503-3508.
[2]XiaoB,MaJF,WangX.ImageanalysisbyBessel-Fouriermoments[J].PatternRecognition,2010(43):2620-2629.
[3]LingH,JacobsDW.Shapeclassificationusingtheinnerdistance[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2007,29(2):286-299.
[4]HuR,JiaW,LingH,etal.MultiscaleDistanceMatrixforFastPlantLeafRecognition[J].IEEETrans.ImageProcessing,2012,21(11):4667-4172.
[5]MikolajczykK,SchmidC.Aperformanceevaluationoflocaldescriptors[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2005(27):1615-1630.
[6]MikolajczykK,SchmidC.Scale&affineinvariantinterestpointdetectors[J].InternationalJournalofComputerVision,2004(60):63-86.
[7]LoweDG.Distinctiveimagefeaturesfromscale-invariantkeypoints[J].InternationalJournalofComputerVision,2003,60(2):91-11.
[8]BayH,EssA,TuytelaarsT,etal.Speeded-uprobustfeatures(SURF)[J].ComputerVisionandImageUnderstanding,2008,110(3):346-359.
[9]TuytelaarsT,MikolajczykK.Localinvariantfeaturedetectors:Asurvey[J].FoundationsandTrendsinComputerGraphicsandVision,2007,3(3):177-280.
[10]BadrinathGS,PhalguniGupta.PalmprintVerificationusingSIFTfeatures[J].ImageProcessingTheory,ToolsandApplications,2008(20):1-8.
[11]LeqingZhu,SanyuanZhang,RuiXing,etal.UsingSIFTandPROSACtoIdentifyPalmprints[C]//Proceedingsofthe2008InternationalConferenceonImageProcessing,ComputerVision,&PatternRecognition,2008:136-141.
[12]XuY,HuangSB,JiH,etal.Scale-spacetexturedescriptiononSIFT-liketextons[J].ComputerVisionandImageUnderstanding,2012(116):999-1013.
[13]HeY,KavukcuogluK,WangY,etal.UnsupervisedFeatureLearningbyDeepSparseCoding[J].arXivpreprintarXiv,2013:1312.5783.
[14]JiangZ,LinZ,DavisLS.LearningadiscriminativedictionaryforsparsecodingvialabelconsistentK-SVD[C]//ComputerVisionandPatternRecognition(CVPR),2011IEEEConferenceon.IEEE,2011:1697-1704.
[15]LazebnikS,SchmidC,PonceJ.Beyondbagsoffeatures:Spatialpyramidmatchingforrecognizingnaturalscenecategories[C]//ComputerVisionandPatternRecognition,2006IEEEComputerSocietyConferenceon.IEEE,2006,2:2169-2178.
[16]ZhouX,CuiN,LiZ,etal.Hierarchicalgaussianizationforimageclassification[C]//ComputerVision,2009IEEE12thInternationalConferenceon.IEEE,2009:1971-1977.
[17]YangJ,YuK,GongY,etal.Linearspatialpyramidmatchingusingsparsecodingforimageclassification[C]//ComputerVisionandPatternRecognition,2009.CVPR2009.IEEEConferenceon.IEEE,2009:1794-1801.
[18]WangJ,YangJ,YuK,etal.Locality-constrainedlinearcodingforimageclassification[C]//ComputerVisionandPatternRecognition(CVPR),2010IEEEConferenceon.IEEE,2010:3360-3367.
[19]ZhangL,MaC.Low-rankdecompositionandLaplaciangroupsparsecodingforimageclassification[J].Neurocomputing,2014(135):339-347.
[20]LiuB,LiuJ,LuH.Adaptivespatialpartitionlearningforimageclassification[J].Neurocomputing,2014(142):282-290.
[21]ZhangC,WangS,HuangQ,etal.Imageclassificationusingspatialpyramidrobustsparsecoding[J].PatternRecognitionLetters,2013,34(9):1046-1052.
[22]KeY,SukthankarR.PCA-SIFT:Amoredistinctiverepresentationforlocalimagedescriptors[C]//ComputerVisionandPatternRecognition,2004.CVPR2004.Proceedingsofthe2004IEEEComputerSocietyConferenceon.IEEE,2004:506-513.
[23] 王晅,马建峰.数字图像分析与模式识别[M].北京:科学出版社,2009.
[24]FeifeiL,FergusR,PeronaP.Learninggenerativevisualmodelsfromfewtrainingexamples:anincrementalBayesianapproachtestedon101objectcategories[C]//IEEECVPRWorkshoponGenerative-ModelBasedVision,2004.
IMAGE CLASSIFICATION ALGORITHM BASED ON PCA-SIFT FEATURESANDBAYESIANDECISION
Tu QiujieWang Xuan
(School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,Shaanxi,China)
AbstractIn order to cope with the problems that existing SIFT-based image classification algorithms require a large amount of storage space and are sensitive to image backgrounds, this paper presents a novel image classification algorithm which is based on PCA-SIFT features and Bayesian decision. The algorithm first applies the principal component analysis (PCA) to reduce the dimensionality of SIFT from 128 to 36, in training process, it makes regional matching on PCA-SIFT descriptors of the training sample images. In order to improve its robustness on background image interference, we selected the stable PCA-SIFT descriptors in object images based on their matching rates, and then used the maximum likelihood estimation to estimate the probability distribution parameters. Finally we used Bayesian decision theory to implement the image classification. Simulation experiment showed that this algorithm has higher classification accuracy compared with existing SIFT-based image classification methods. It also has minimum storage space requirement and higher computation efficiency.
KeywordsPCA-SIFTClusteringBayesian decisionImage classification
收稿日期:2014-12-30。涂秋洁,硕士生,主研领域:数字图像处理,模式识别。王晅,教授。
中图分类号TP3
文献标识码A
DOI:10.3969/j.issn.1000-386x.2016.06.052

