基于GPU的图形学加速算法在离散元法中的应用

鲍春永　赵啦啦　刘万英　杨康康

(中国矿业大学机电工程学院　江苏 徐州 221008)



基于GPU的图形学加速算法在离散元法中的应用

鲍春永赵啦啦刘万英杨康康

(中国矿业大学机电工程学院江苏 徐州 221008)

摘要颗粒离散元法是一种广泛应用于研究颗粒物料力学行为的数值模拟方法，而计算效率是制约其发展和应用的主要因素之一。通过Pro/E软件建立了料斗模型，利用Stream DEM软件对料斗的颗粒充填过程进行离散元法模拟研究，并对基于CPU和GPU加速算法的运算过程和结果进行对比。结果表明，基于GPU的计算机图形学加速算法可大幅提高颗粒离散元法模拟过程的运算效率。当填充颗粒数量达到13万时，其运算效率比基于CPU的运算效率提高了10倍以上。

关键词离散元法图形学算法GPUCPU

0引言

离散元法DEM(discreteelementmethod)发起于20世纪70年代。作为一种数值方法，主要用于模拟离散颗粒组合体在准静态和动态条件下的变形及破坏过程，在包括岩石力学、土力学、岩土工程、颗粒运输、脆性材料加工、物料分选等散体工程技术领域得到成功推广和使用，是目前研究颗粒系统力学行为的有效数值方法。通过离散元方法能够得到不容易测量的颗粒级微观信息，如颗粒在运动过程中的位置、速度、加速度、受力状态等。这给研究人员提供颗粒离散物质的微观以及宏观信息，进而取代部分的物理实验，减少在人力，物力以及能源损耗上的投入。经过长时间的发展，离散元法作为一种研究颗粒系统运动行为的数值方法，在国内外已经得到广泛的应用[1-3]。

基于离散元法的模拟运算过程中包含了大量的计算机图形学算法问题，比如，颗粒群的生成、颗粒碰撞检测预处理等。当利用离散元法对大数量的颗粒系统进行数值模拟时，计算机的运算量和数据存储量都将随着颗粒数量的增加而成几何级数的增长，从而导致整个模拟过程费时费力。解决颗粒数量对离散元计算的限制已成为离散元法应用和发展过程中亟待解决的重要问题之一[4-6]。

随着GPU技术的发展，GPU除了应用于图形处理外，还能用于应用计算。GPU的并行处理功能能够在很大程度上提高计算速度。基于GPU的加速算法已经在动画绘制、体绘制等方面取得了应用[7,8]。因此，基于GPU的计算机图形学加速算法为解决离散元法应用中大量颗粒的高效运算问题提供了一个新方法。

基于此，本文将基于GPU的计算机图形学加速算法应用于颗粒离散元法模拟过程中，建立起了料斗的颗粒充填模型。并基于CPU和GPU两种不同运算方法对料斗充填过程进行数值模拟。并对模拟过程的运算时间进行比较，验证基于GPU的计算机图形学加速算法应用于颗粒离散元法模拟的可行性和有效性。

1颗粒离散元法基本原理

颗粒离散元法是由Cundall和Strack在1979年提出的研究离散颗粒物质结构和运动规律的一种数值方法，其思想起源于分子动力学。与以弹性体力学和流体力学为基础的连续介质理论对颗粒物质的描述不同，颗粒离散元法把所要研究的对象分离为刚性元素的集合，使每个元素满足牛顿第二定律，用中心差分的方法求解各元素的运动方程，得到颗粒组合的整体运动状态。颗粒离散元法理论来自于Hertz和Mindlin-Deresiewicz的球形颗粒接触理论，使用简化的软球和硬球颗粒的接触模型，实现对颗粒物质的运动以及各种微观行为的数值计算[9]。

颗粒离散元法的基本计算流程如图1所示。

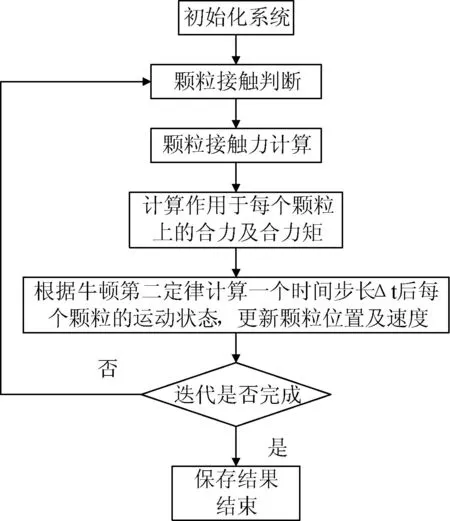
图1　颗粒离散元法求解流程图

其计算过程为：

(1) 初始化系统，对每个颗粒给定一个起始时间时的初始位置以及初始速度，并给定数值计算的时间步长；

(2) 对颗粒进行碰撞接触检测，确定当前时刻系统中的所有碰撞接触，通常分为空间划分和空间判定两步：

(3) 根据第(2)步中的碰撞接触检测结果，计算碰撞颗粒间的接触力；

(4) 进一步计算作用于每个颗粒上的合力以及合力矩；

(5) 根据牛顿第二运动定律，结合给定的计算时间步长，利用迭代算法，更新颗粒的位置、速度和加速度等参数，同时数值计算的时间增加一个时间步长；

(6) 如果迭代计算完成，则保存计算结果并退出程序，否则继续进行颗粒接触判断，循环执行。

由上述颗粒离散元法求解过程可知，当颗粒数量大幅度增加时，颗粒群的生成和接触判断所需要的计算量将快速增大，计算资源将被大量地占用，从而导致颗粒离散元法求解过程中的效率降低，计算过程所用时间过长。因此，解决颗粒数量对离散元计算过程的影响已成为离散元法应用和发展过程中所面临的重要问题之一。

2基于GPU的加速算法原理

图形图像的负载包括复杂顶点、几何图形和像素处理任务图等，这些负载是高度并行的，适合于多核高延迟的多线程处理。GPU作为一种专门的多线程并行处理器，其流处理器对于高效处理大规模的像素点，有其特有的优势。同时，对于CUDA(ComputeUnifiedDeviceArchitecture)的开发解决了GPU编程问题。运用CUDA的编码架构，可以让编码器从复杂的SAD(SumofAbsoluteDifferences)计算中释放，将计算过程交由具有并行处理能力的GPU执行，CPU只执行选择控制和逻辑控制。传统的信息处理模式是在CPU上进行的，然而当处理的信息量较大时，就会出现运行缓慢的问题，GPU快速计算的编程能力和CUDA并发执行的特点可以很好地解决这一问题。CUDA使用新的计算体系结构来利用GPU硬件资源，能够实现比CPU更加优越的大规模的数据计算能力。CUDA采用C语言作为编程语言提供大量的高性能计算指令开发能力，使开发者能够在GPU的强大计算能力的基础上建立起一种效率更高的密集数据计算解决方案[10-12]。

与传统的依靠CPU进行图像动画渲染计算的服务器相比，基于GPU运算的宗旨是实现图形加速，其设计的主要目的是优化图形加速的相关运算，如z-buffering消隐、纹理映射、图形的坐标位置变换与光照计算等。基于GPU的计算偏重于图形渲染运算和大规模并行计算，依靠集群服务器实现实时光线追踪渲染，从而保证图形图像的最终现实效果[13-15]。

3料斗充填过程的离散元法模拟

3.1料斗模型的建立

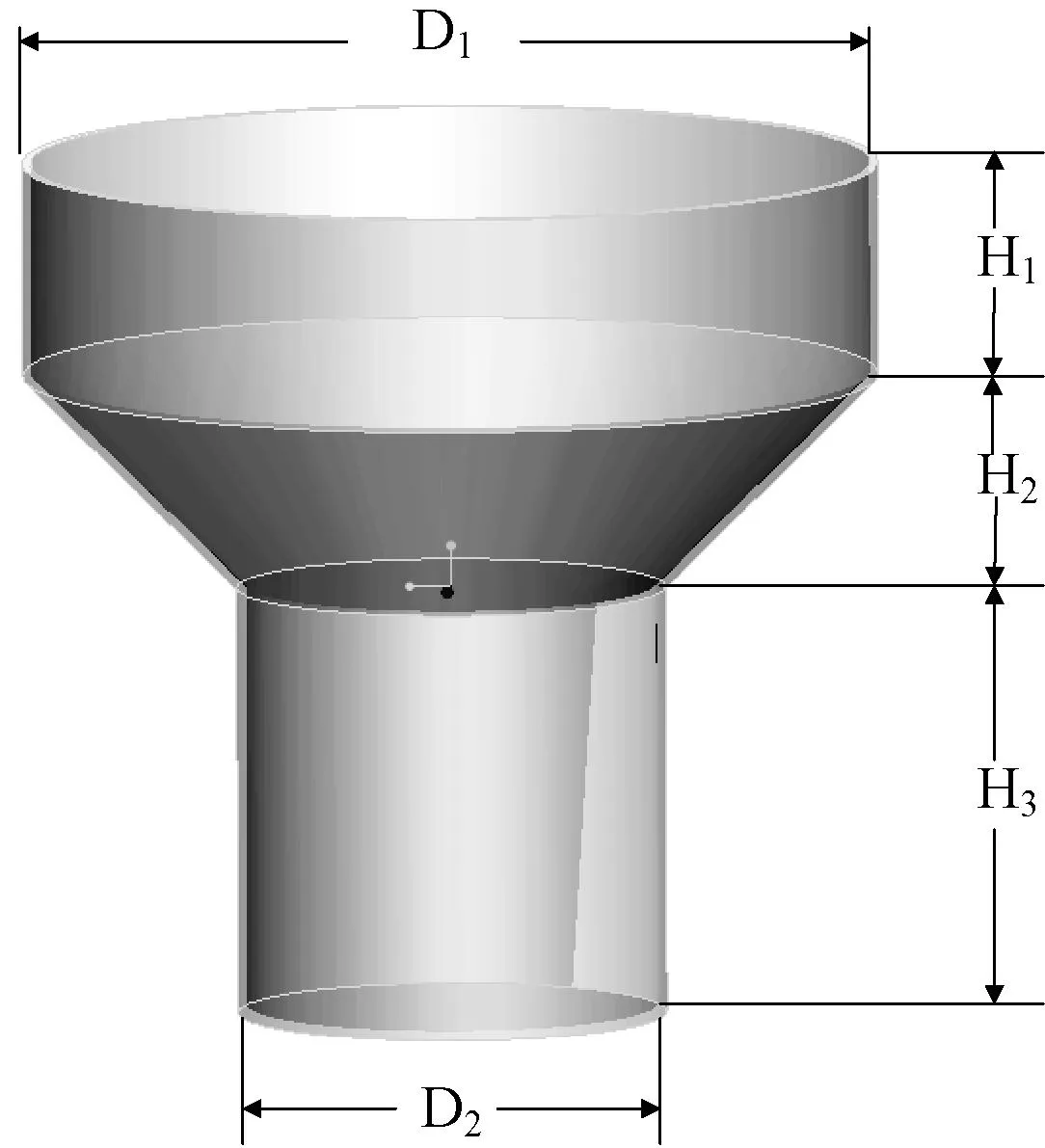
图2　料斗几何模型

本文利用Pro/E软件建立了料斗的几何模型，并将该模型作为离散元法模拟的颗粒充填的容器，其结构形状如图2所示。其中，料斗模型的总体高度为2000mm，料斗大端圆柱体直径D1为2000mm，大端圆柱体高H1为500mm，小端圆柱体直径D2为1000mm，小端圆柱体高H3为1000mm。

利用StreamDEM软件建立模拟运算的虚拟边界。新建圆柱几何模型，其半径为1000mm，高为1000mm，并将其设置为虚拟边界，适当移动虚拟边界的位置，使其与料斗几何模型的大端圆柱体平齐。充填颗粒的材料属性设置为煤块[16]，颗粒粒径分布采用等粒径分布，颗粒碰撞模型为HertzModel，静态填充率设置为0.2。本文采用通过改变粒径大小的方法来获得不同的充填颗粒数量。表1给出了模拟过程中所采用的不同颗粒粒径以及颗粒粒径对应的颗粒数量。

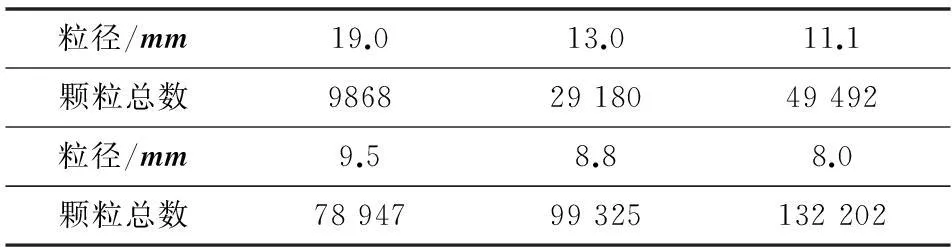
表1　不同颗粒粒径所对应的颗粒数量

3.2充填过程模拟及结果

利用StreamDEM离散元仿真软件进行模拟运算。将上述利用Pro/E软件所建立的料斗几何模型转化为.stl图形格式并导入StreamDEM软件中，对颗粒的充填过程进行模拟。模拟过程中，分别采用StreamDEM软件中内置的CPU处理器和GPU处理器的功能模块进行运算。基于CPU处理器运算时，所利用的硬件为英特尔G41ExpressChipset(1GB/戴尔OptiPlex380MiniTower)。基于GPU处理器运算时，所利用的硬件为NVIDIAGeForceGTX650显卡。模拟运算的时间步长设置为1.0～0.5s，输出间隔为0.1s，总物理时长设置为1s。

颗粒充填料斗过程的离散元法模拟结果如图3所示。其中，(a)为基于CPU处理器的充填过程模拟结果，(b)为基于GPU处理器的充填过程模拟结果。根据所得的模拟结果，可获得基于CPU处理器和GPU处理器的不同数量颗粒完成充填所需的运算时间，其对比情况如图4所示。

图3　颗粒充填料斗过程的离散元法模拟

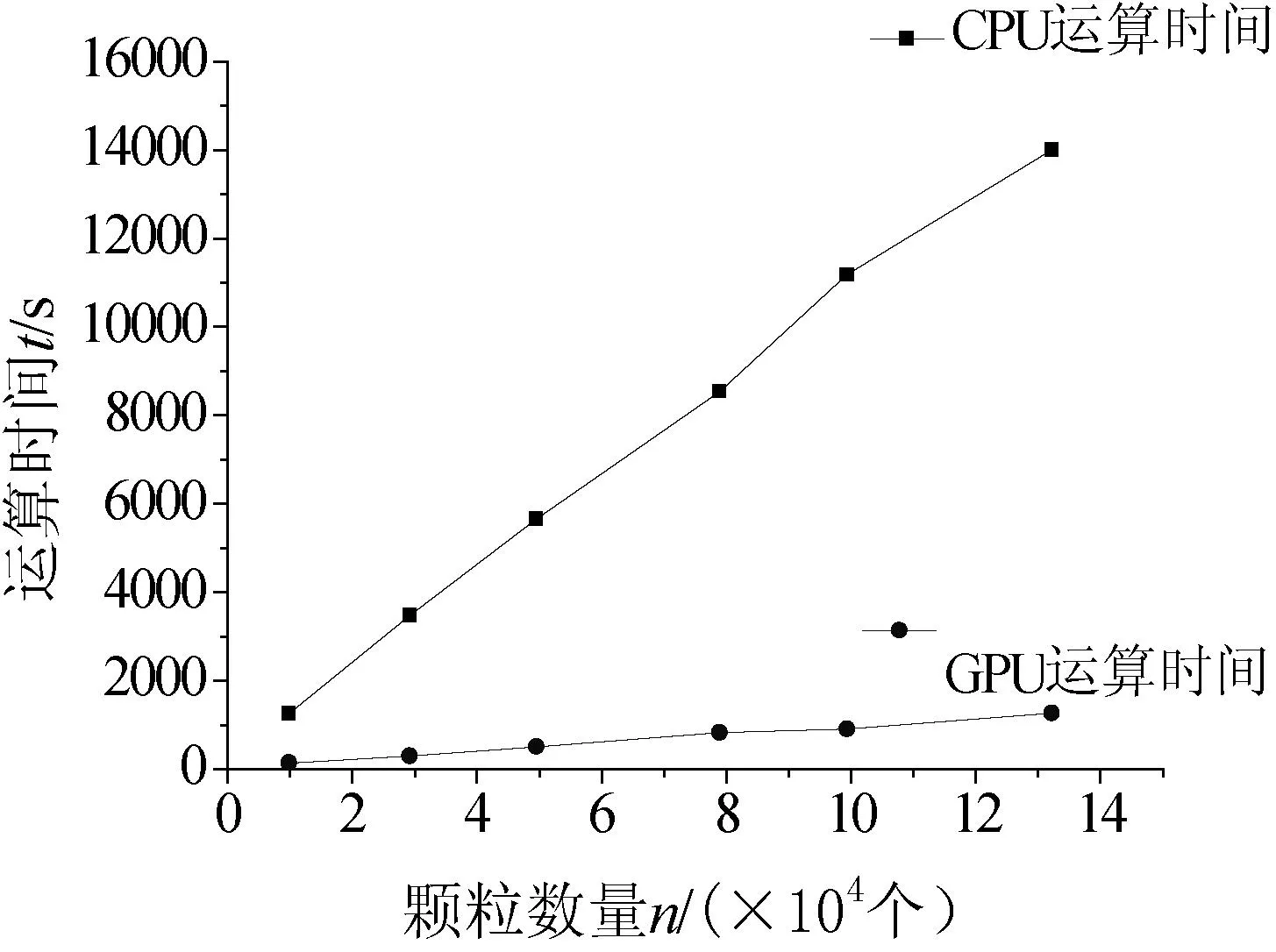
图4　基于CPU和GPU的料斗充填过程运算时间

由图4可以看出，基于CPU处理器进行模拟时，所需的运算时间随着颗粒数量的增多而快速增加。而基于GPU处理器进行模拟时，所需的运算时间随着颗粒数量的增多而缓慢增加。当颗粒数量相同时，基于CPU处理器模拟所需时间均多于基于GPU处理器模拟所需时间，并且随着颗粒数量的增加，两者的运算效率差别越显著。当颗粒数量约为1万个时，CPU运算需要1258s，而GPU运算仅需132s，运算效率相差近10倍。当颗粒数量增加至约为13万个时，CPU运算时间极大增加至14 010s，而GPU运算则仅需1270s，两者运算效率相差达10倍以上。可见，基于图形处理器GPU的加速算法能显著提高离散元法的运算效率。

4结语

本文利用StreamDEM离散元仿真软件对料斗的颗粒充填过程进行了数值模拟，并对基于CPU和基于GPU加速算法的运算过程进行了比较，得出以下结论：

(1) 随着模拟颗粒数量的增加，基于CPU的运算时间急剧增加，而基于GPU的运算时间则缓慢增加。当颗粒数量相同时，基于GPU的计算机图形学加速算法的运算效率比基于CPU的运算效率提高了10倍。

(2) 基于GPU的计算机图形学加速算法可显著提高离散元程序的运算效率，为提高大数量颗粒系统的离散元法模拟效率提供了新方法。

参考文献

[1] 赵啦啦,赵跃民,刘初升,等.湿颗粒堆力学特性的离散元法模拟研究[J].物理学报,2014,63(3):265-273.

[2] 田瑞霞,焦红光,白璟宇.离散元法在矿物加工工程中的应用现状[J].选煤技术,2012,2(1):72-76.

[3]ZhuHP,ZhouZY,YangRY.Discreteparticlesimulationofparticulatesystems:Areviewofmajorapplicationsandfindings[J].ChemicalEngineeringScience,2007,62(13):3378-3396.

[4] 徐佩华,黄润秋,邓辉.颗粒离散元法的颗粒破碎研究进展[J].工程地质学报,2012,20(3):410-418.

[5] 赵魏,邹声勇,姬建刚,等.离散元法在磨机设计中的应用[J].矿山机械,2013,41(2):66-70.

[6] 赵啦啦.振动筛分过程的三维离散元法模拟研究[D].徐州:中国矿业大学,2010.

[7] 王妙一,王斌,雍俊海.GPU上的水彩画风格实时渲染及动画绘制[J].图学学报,2012,33(3):73-79.

[8] 袁斌.基于曲率的GPU光线投射[J].图学学报,2012,33(6):24-30.

[9] 王国强,郝万军,王继新.离散单元法及其在EDEM上的实践[M].西安:西北工业大学出版社,2010.

[10] 张云泉,张先轶,贾海鹏,等.OpenCL异构计算[M].2版.北京:清华大学出版社,2013.

[11] 苏统华,李东,李松泽,等.CUDA并行程序设计-GPU编程指南[M].北京:机械工业出版社,2014.

[12] 姚勇,王小琴.GPU精粹-实时图形编辑的技术、技巧和技艺[M].北京:人民邮电出版社,2006.

[13] 杨柏林,陈根浪,王聪.GPU精粹3[M].北京:清华大学出版社,2010.

[14] 刘旭江,徐圆,齐洪亮,等.基于GPU的医学图像多功能可视化的实现[J].计算机应用与软件,2013,30(5):52-55,64.

[15] 郑晓薇,侯立斐,于梦玲.GPU并行计算在LSSVM股票预测上的研究与应用[J].计算机应用与软件,2013,30(1):34-36.

[16] 胡国明.颗粒系统的离散元素法分析仿真:离散元素法的工业应用与EDEM软件简介[M].武汉:武汉理工大学出版社,2010.

APPLICATION OF GPU-BASED GRAPHICS ACCELERATION ALGORITHMINDISCRETEELEMENTMETHOD

Bao ChunyongZhao LalaLiu WanyingYang Kangkang

(School of Mechanical and Electrical Engineering,China University of Mining and Technology,Xuzhou 221008,Jiangsu,China)

AbstractParticle discrete element method is a kind of numerical simulation method widely used in the research of granular material mechanics behaviour. Computation efficiency is one of the main factors that restricts its development and application. In this paper, we build a hopper model by using Pro/E software, and use Stream DEM software to study the stimulations of discrete element method in regard to hopper’s particles filling process. We also compare the operation processes and results of CPU-based and GPU-based acceleration algorithms. Results show that the GPU-based computer graphics acceleration algorithm can dramatically improve the computation efficiency of the simulation process of particle discrete element method. When the number of particles to be filled reaches 130 000, its computational efficiency improves over 10 times than that of the CPU-based acceleration algorithm.

KeywordsDiscrete element methodGraphics algorithmGPUCPU

收稿日期：2014-10-27。国家自然科学基金青年科学基金项目(51204181)；高等学校博士学科点专项科研基金项目(20110095120004)；中国博士后科学基金项目(20110491485，2013T60576)；中央高校基本科研业务费专项资金项目(2011QNA10)；江苏高校优势学科建设工程课题。鲍春永，硕士生，主研领域：计算机图形学理论，离散元法模拟。赵啦啦，副教授。刘万英，硕士生。杨康康，硕士生。

中图分类号TP301.4

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.018